2)Метод касательных (Ньютона).
,
где
x0=a,
если f(a)×f’’(x)>0;
x0=b,
если f(b)×f’’(x)>0
на [a;b].
1-е задание: tg(0,55x+0,1)=x2 , где х[0,6;0,8] (см. решение выше).
Так
как f(0,6)>0,
f(0,8)<0,
f’’(x)<0,
то за начальное приближение берём
х0=0,8.
Вычисления производим по формуле:
f’(0,8)=0,55/(cos2(0,55x+0,1))-2x=-0,8523.
Вычисления производим в виде таблицы:
|
n |
xn |
|
f’(x)=0,55/(cos2(0,55x+0,1))-2x |
|
|
0 |
0,8 |
-0,04057 |
-0,85238 |
0,047597 |
|
1 |
0,752403 |
-0,001724 |
-0,77961 |
0,002211 |
|
2 |
0,750192 |
0,00000 |
-0,77619 |
0,00000 |
Ответ: х0,750
2-е задание: f(x)=x3-0,2x2+0,5x+1,5 f’(x)=3x2-0,4x+0,5
Так как f(0)>0, f(-1)<0, f’’(x)<0, то за начальное приближение берём х0=-1.
|
n |
xn |
f(x)=x3-0,2x2+0,5x+1,5 |
f’(x)=3x2-0,4x+0,5 |
|
|
0 |
-1 |
-0,2 |
3,9 |
-0,05128 |
|
1 |
-0,94872 |
-0,008281 |
3,579684 |
-0,00231 |
|
2 |
-0,9464 |
-0,00000 |
3,565608 |
-0,00000 |
Ответ: х-0,946
Лабораторная работа №5 «Комбинированный метод»
Комбинированным
методом решить уравнение, вычислив
корни с точностью до 
.
1.
.
16. 
.
2.
.
17. 
.
3.
.
18. 
.
4.
.
19. 
.
5.
.
20. 
.
6.
.
21. 
.
7.
.
22. 
.
8.
.
23. 
.
9.
.
24. 
.
10.
.
25. 
.
11.
.
26. 
.
12.
.
27. 
.
13.
.
28. 
.
14.
.
29. 
.
15.
.
30. 
.
Пример
6. Комбинированным
методом решить уравнение 
,
вычислив корни с точностью до 
.
Решение.
а) Отделим корни аналитически:
;
.
Вычислим корни производной:
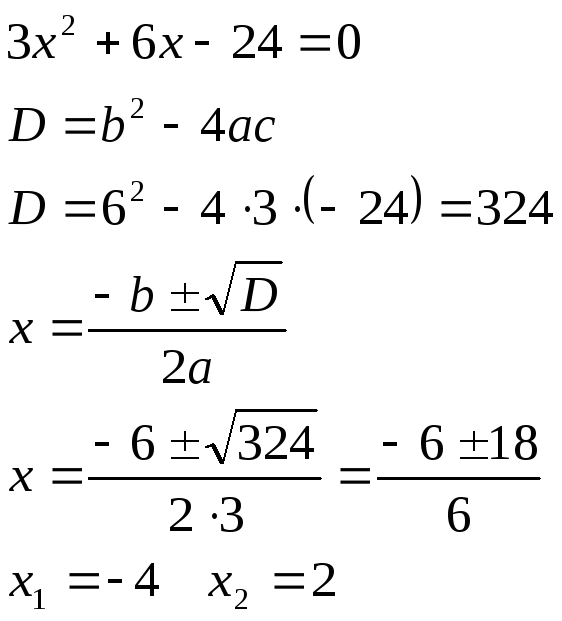
Составляем
таблицу знаков функции 
,
полагая 
равным: а) критическим значениям функции
(корням производной) или близким к ним;
б) граничным значениям (исходя из области
определения функции):
|
|
|
-4 |
2 |
|
|
|
- |
+ |
- |
+ |
Т.к. происходят три перемены знака функции, то уравнение имеет три действительных корня. Чтобы завершить операцию отделения корней, следует уменьшить промежутки, содержащие корни, так чтобы их длина была не больше 1. Для этого составим новую таблицу знаков функции:
|
|
|
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
- |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
- |
+ |
+ |
Отсюда видно, что корни уравнения находятся в следующих промежутках:
.
б)
Уточним корень
:
;
;
при 
;
при 
;
,
следовательно, методом хорд получаем
значение корня с избытком, а методом
касательных – с недостатком, т.е. слева
применяем метод касательных, справа –
метод хорд.
Тогда используем формулы:
,
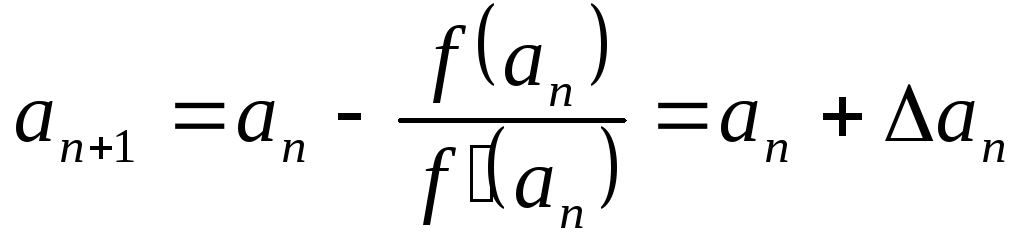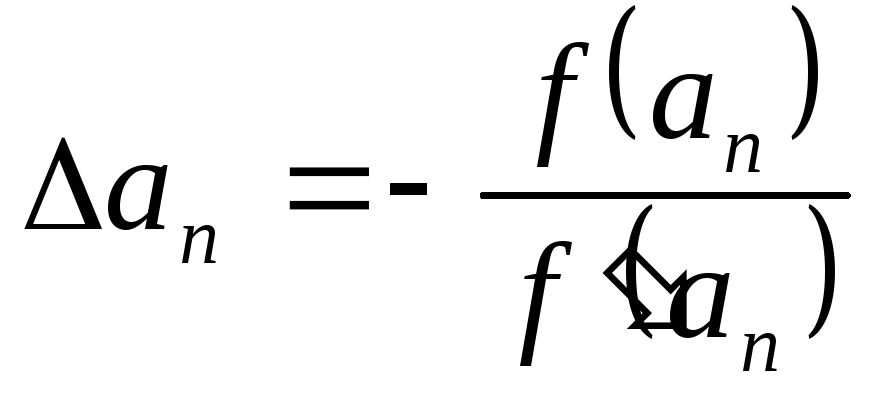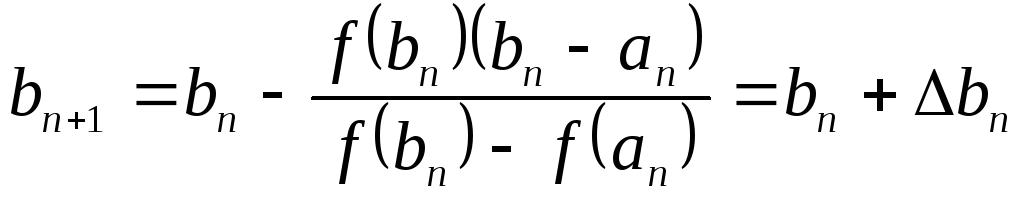где 
;
,
где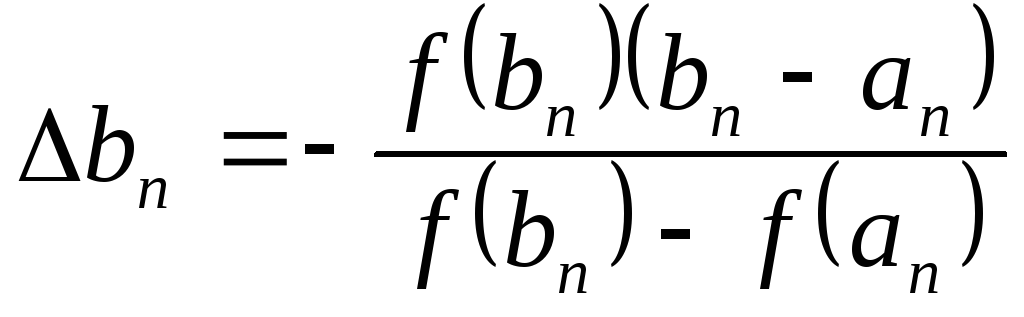 
.
Вычисления будем вести в таблице:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-7 |
-6 |
1 |
-26 |
38 |
81 |
64,0000 |
0,3210 |
-0,5938 |
|
1 |
-6,6790 |
-6,5938 |
0,0853 |
-1,8215 |
4,0026 |
69,7535 |
5,8241 |
0,0261 |
-0,0586 |
|
2 |
-6,6529 |
-6,6523 |
0,0006 |
|
|
|
|
|
|
Т.к.
,
то вычисления прекращаем.
Тогда истинный корень уравнения:
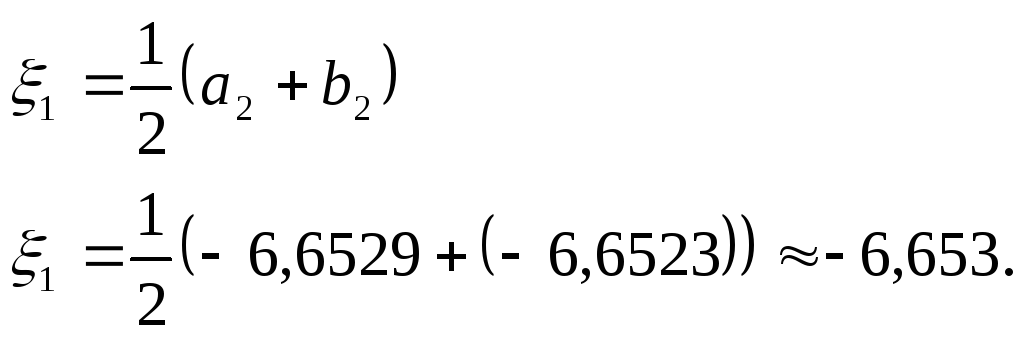
в)
Уточним корень
:
;
;
при
;
при
.
,
следовательно, методом хорд получаем
значение корня с избытком, а методом
касательных – с недостатком, т.е. слева
применяем метод касательных, справа –
метод хорд.
Тогда используем формулы:
,
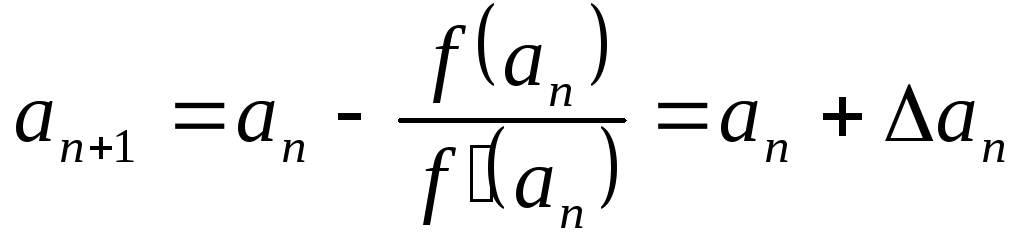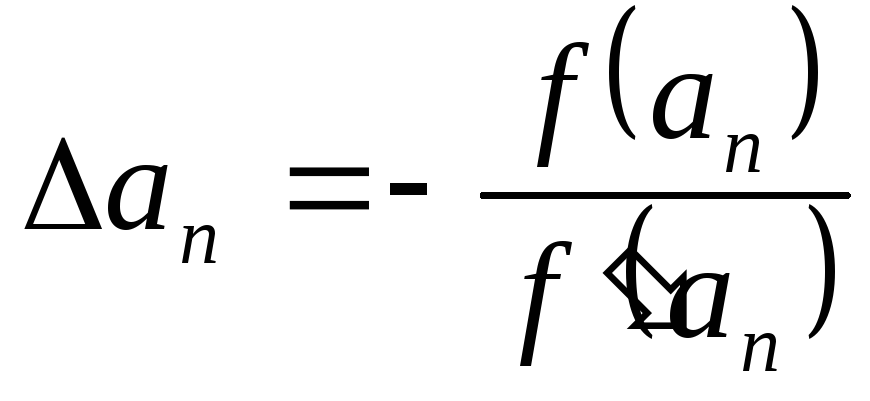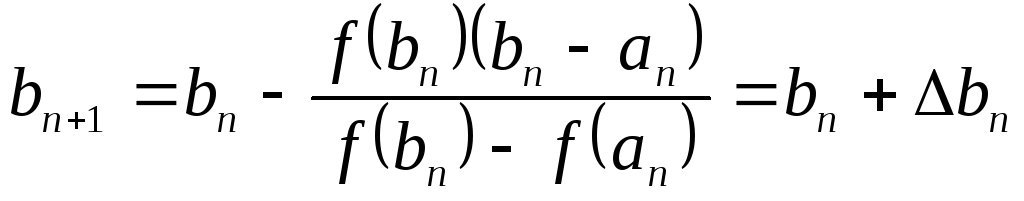где 
;
,
где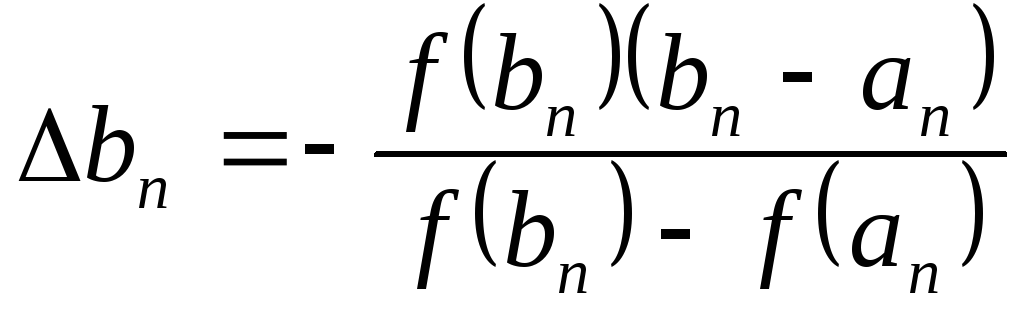 
.
Вычисления будем вести в таблице:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
2 |
-18 |
-24 |
-20,0000 |
0,0833 |
-0,9000 |
|
1 |
0,0833 |
0,1000 |
0,0167 |
0,0214 |
-0,3690 |
-23,4792 |
-0,3904 |
0,0009 |
-0,0158 |
|
2 |
0,0842 |
0,0842 |
0,0000 |
|
|
|
|
|
|
Т.к.
,
то вычисления прекращаем.
Тогда истинный корень уравнения:
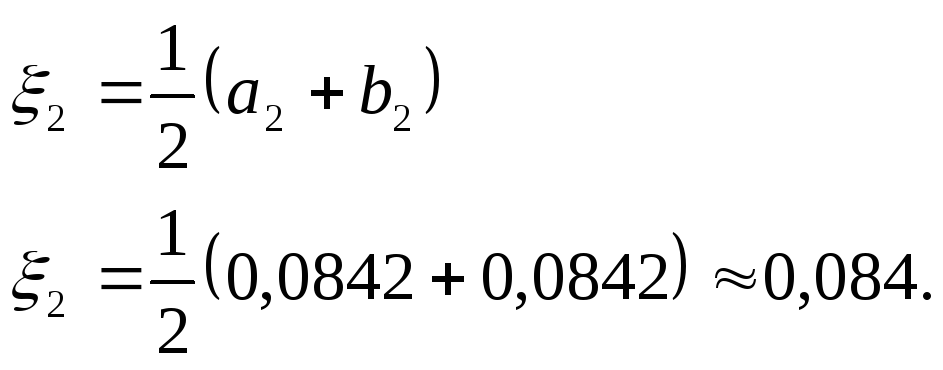
г)
Уточним корень 
:
;
;
при 
;
при 
.
,
следовательно, методом хорд получаем
значение корня с недостатком, а методом
касательных – с избытком, т.е. слева
применяем метод хорд, справа – метод
касательных.
Тогда используем формулы:
,
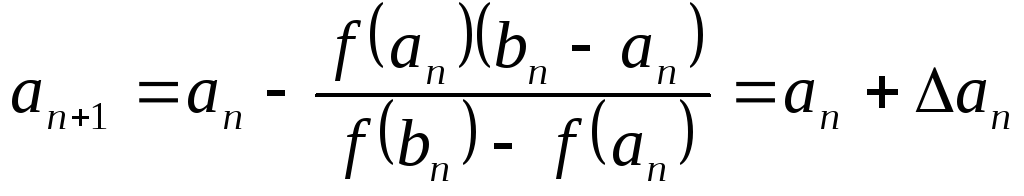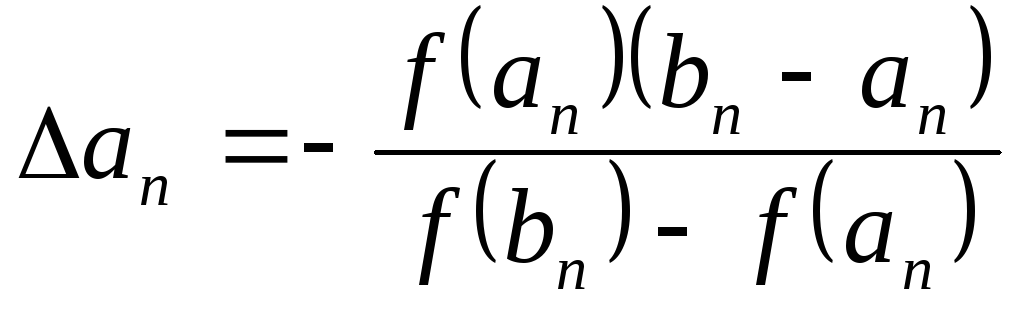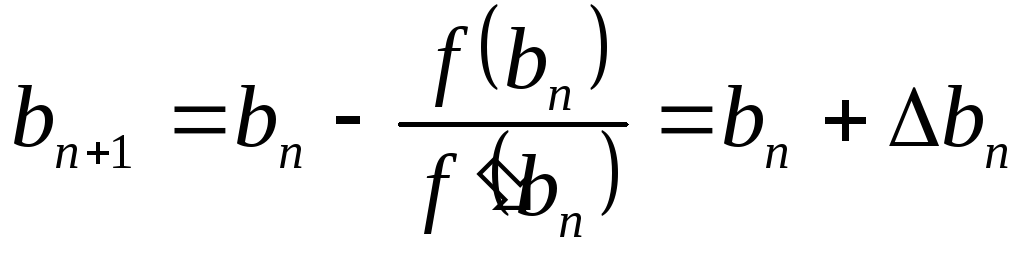где 
;
,
где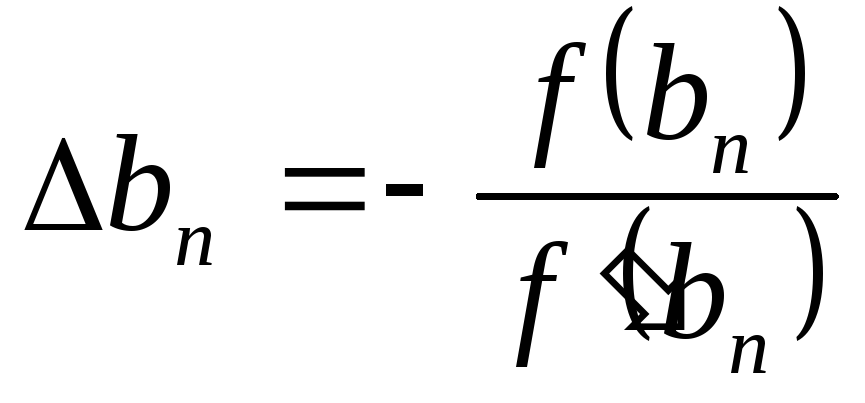 
.
Вычисления будем вести в таблице:
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
4 |
1 |
-16 |
18 |
48 |
34,0000 |
0,4706 |
-0,3750 |
|
1 |
3,4706 |
3,6250 |
0,1544 |
-3,3560 |
2,0566 |
32,9585 |
5,4126 |
0,1018 |
-0,0587 |
|
2 |
3,5724 |
3,5663 |
-0,0061 |
0,1401 |
-0,0767 |
35,7209 |
-0,2169 |
-0,0039 |
0,0022 |
|
3 |
3,5685 |
3,5685 |
0,0000 |
|
|
|
|
|
|
Т.к.
,
то вычисления прекращаем.
Тогда истинный корень уравнения:
