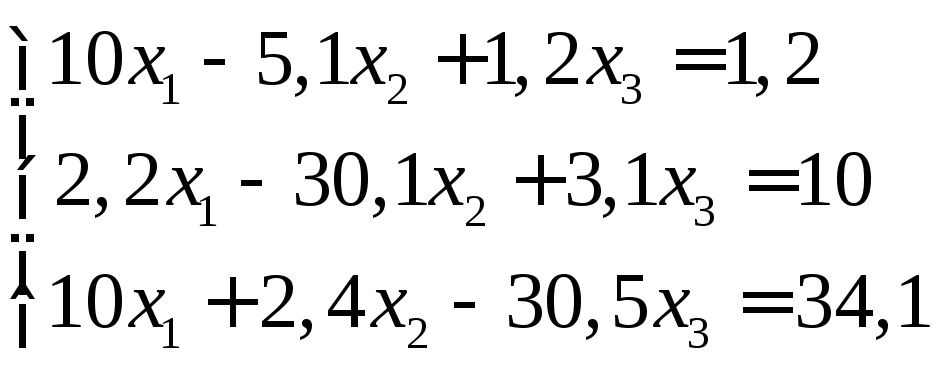- •Лабораторная работа №1 «Элементарная теория погрешностей»
- •Лабораторная работа №2 «Элементарная теория погрешностей»
- •Лабораторная работа №3 «Метод половинного деления»
- •Лабораторная работа №4: «Решение нелинейных уравнений методом хорд и касательных».
- •2)Метод касательных (Ньютона).
- •Лабораторная работа №5 «Комбинированный метод»
- •Лабораторная работа №6: «Решение нелинейных уравнений методом простой итерации».
- •Метод главных элементов для решения системы уравнений
- •Лабораторная работа №8 «Метод Гаусса»
- •Лабораторная работа №9 «Метод Халецкого»
- •Порядок заполнения таблицы:
- •Лабораторная работа №10 «Метод квадратных корней»
- •Лабораторная работа №11 «Метод итераций»
- •Лабораторная работа № 12 «Метод Зейделя»
- •Лабораторная работа13. Интерполирование функции многочленом Лагранжа.
- •Лабораторная работа14. Интерполирование функции многочленом Ньютона.
- •Лабораторная работа15. Сплайновая интерполяция.
- •Лабораторная работа16 Интерполяция функции кубическим сплайном. Метод прогонки.
- •Образец выполнения задания:
- •Лабораторная работа17 Среднеквадратическое приближение
- •Образец выполнения задания:
- •Лабораторная работа18 Ортогональные многочлены Чебышева
- •Образец выполнения задания:
- •Лабораторная работа19. Вычисление определенных интегралов по формуле трапеций и формуле Симпсона, по формуле левых, правых и средних прямоугольников.
- •3) Вычислить определенный интеграл по формуле левых и правых прямоугольников.
- •4) Вычислить определенный интеграл по формуле средних прямоугольников.
- •Лабораторная работа 20. Метод Эйлера с уточнением
- •Л/р 21«Численное решение ду первого порядка методом Рунге-Кутты 4-го порядка».
- •Л/р22 «Решение ду первого порядка методом Адамса-Башфорта».
- •Лабораторная работа 24
- •4. Минимизация функции f(X) методом барьерных функций:
Лабораторная работа №6: «Решение нелинейных уравнений методом простой итерации».
Задание: 1)Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001.
2) Отделить корни уравнения аналитически и уточнить один из них методом итераций с точностью до 0,001.
Пример выполнения задания: 1) 2x+lg(2x+3)=1
Найдём приближённые значения корней графически:
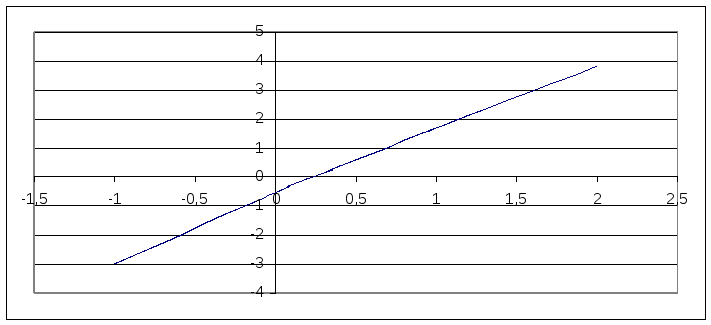
Корень
X0
принадлежит
отрезку [0;0,5]. Для уточнения методом
итерации приведём уравнение к виду:
x=φ(x),
где φ(x)=x-f(x)/k,
считая, что ׀k
׀![]() ,
а Q=max׀'f׀
,
а Q=max׀'f׀
Число k имеет тот же знак, что и f’ в промежутке [0;0,5].
Находим
f(x)=2x+lg(2x+3)-1;
f’(x)=![]()
Q=![]()
![]()
![]() f’(x)>0
при
f’(x)>0
при
![]()
![]()
Примем
k=2,
тогда φ(x)=x-f(x)/k
=x-x-![]()
![]()
За
начальное приближение возьмём x0=0,
все остальные значения будем определять
из равенства:
![]() .
Вычисления удобно располагать в таблице:
.
Вычисления удобно располагать в таблице:![]()
|
n |
xn |
2xn+3 |
lg(2xn+3) |
0,5*lg(2xn+3) |
|
0 |
0 |
3 |
0,477121 |
0,238561 |
|
1 |
0,261439 |
3,5228787 |
0,546898 |
0,273449 |
|
2 |
0,226551 |
3,4531023 |
0,538209 |
0,269105 |
|
3 |
0,230895 |
3,4617906 |
0,539301 |
0,26965 |
|
4 |
0,23035 |
3,4606992 |
0,539164 |
0,269582 |
|
5 |
0,230418 |
|
|
|
Самостоятельно: 1)2x-lgx=7
2)![]()
![]()
Лабораторная работа 7
Метод главных элементов для решения системы уравнений
![]()
a11x1 + a12x2 + a13x3 = a14
a21x1 + a22x2 + a23x3 = a24
a31x1 + a32x2 + a33x3 = a34
На каждом этапе исключения неизвестного выбирают главный элемент ---
Наибольший по модулю коэффициент при неизвестных, затем находят
значения mi, равные частному от деления элементов столбца, содержащих главный элемент, на главный элемент, взятый с противоположным знаком.
Для получения элементов следующего этапа прибавляют главную строку (строку, содержащую главный элемент) к остальным строкам, умножая её на соответствующее значение mi.
Один из возможных вариантов схемы главных элементов приводится ниже.
|
mi |
Коэффициенты при неизвестных
|
Коэффициенты при неизвестных
|
Контрольные суммы | ||
|
x1
|
x2 |
x3 | |||
|
m1 -1 m3 |
a11 a21 a31 |
a12 a22 a32 |
a13 a23 a33 |
a14 a24 a34 |
a15 a25 a35 |
|
-1 m3 |
a’11 a’31 |
a’12 a’32 |
-- -- |
a’14 a’34 |
a’15 a’35 |
|
|
-- |
a”32 |
-- |
a”34 |
a”35 |
|
|
x1 |
x2 |
x3 |
|
|
|
|
X1 |
X2 |
X3 |
|
|
В приведенной схеме Ia23I=maxIaijI, Ia’11I=maxIa’ijI.
Вычисления производят по формулам: m1=-a13/a23, m3=-a33/a23 ;
a’1j= a1j+m1a2j ( j = 1,2,4,5); a’3j= a3j+m3a2j ( j = 1,2,4,5); m’3=-a’31/a’11; a”3j= a’3j+m’3a’1j ( j = 2,4,5);
Неизвестные находят из соотношений:
x2= a”34/a”32 ; X2= a”35/a”32 ;
x1=(a’14– a’12x2)/a’11; X1= (a’15– a’12X2)/a’11;
x3=(a24- a21x1-a22x2)/a23; X3= (a25- a21X1-a22x2)/a23;
Контроль вычислений осуществляют так же, как и в схеме единственного деления.
Задание:
решить систему уравнений с точностью
до ![]() .
.
1.
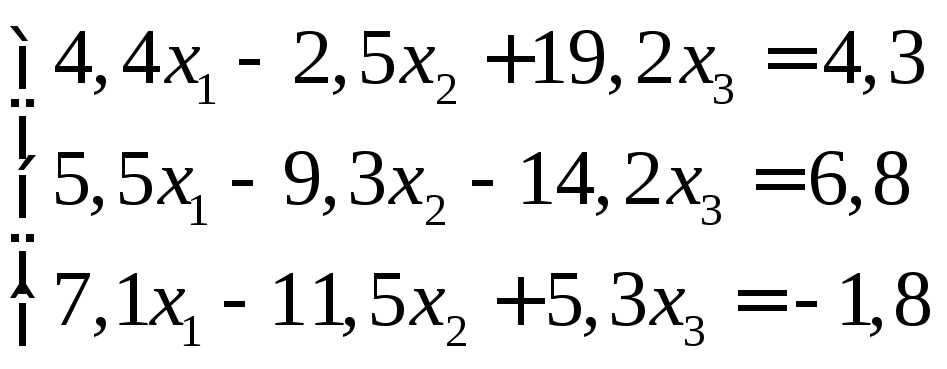 16.
16.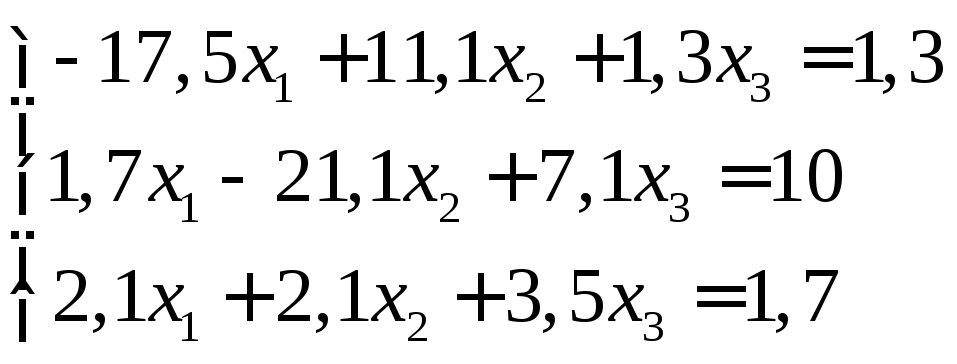
2.
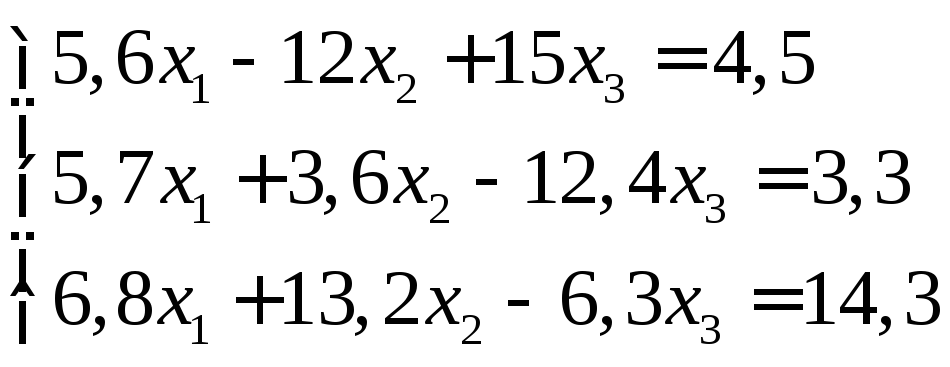 17.
17.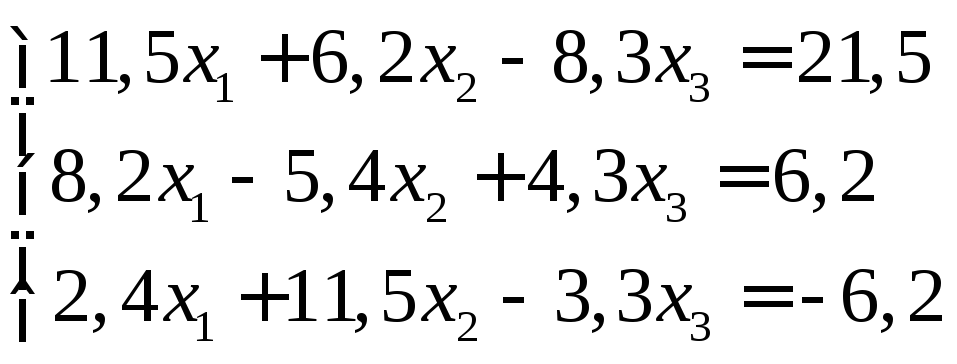
3.
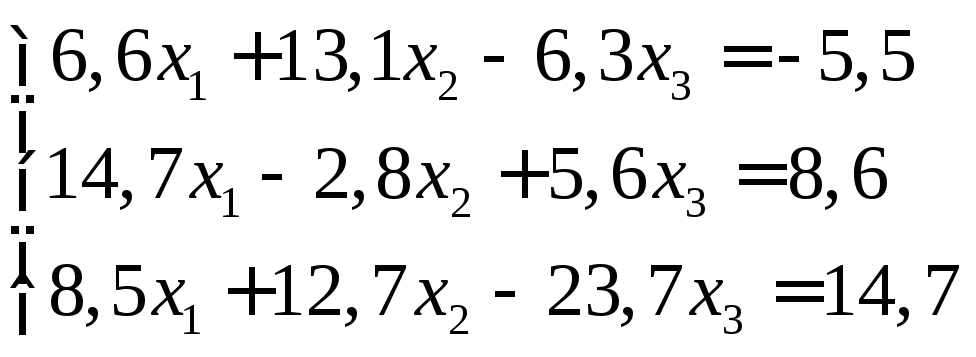 18.
18.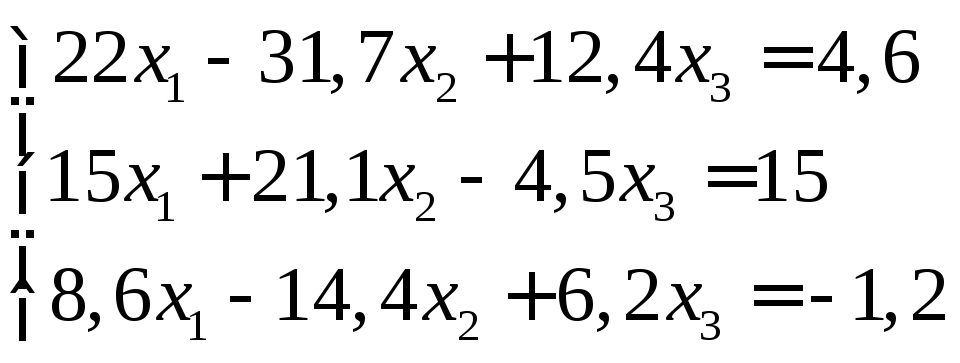
4.
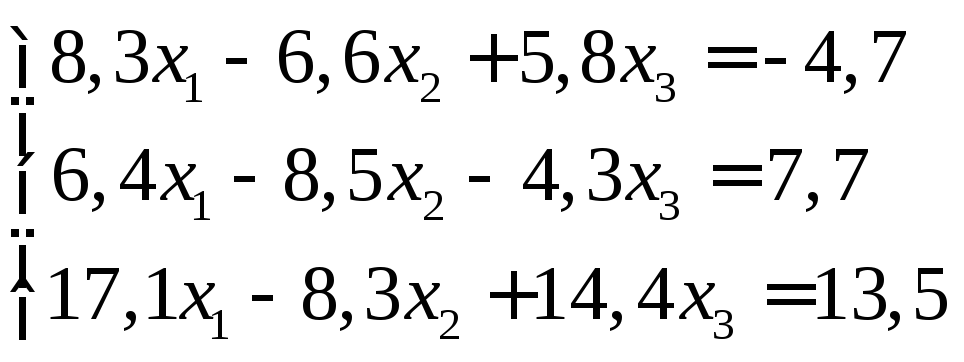 19.
19.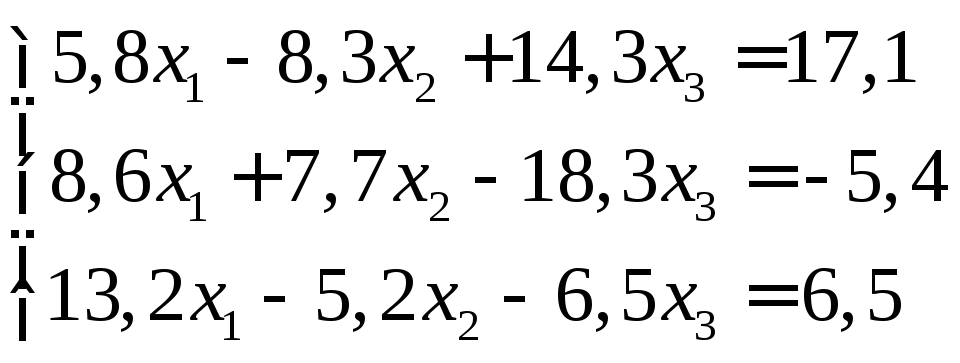
5.
 20.
20.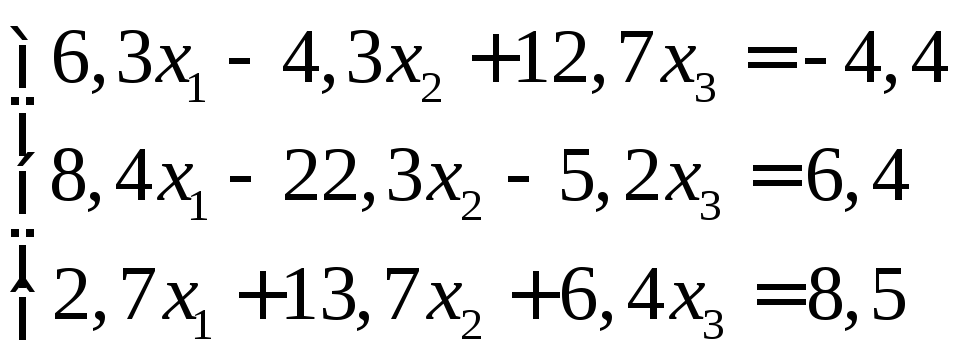
6.
 21.
21.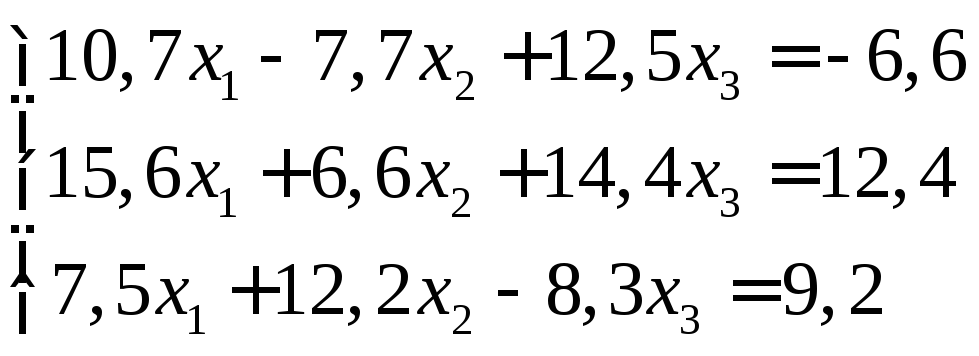
7.
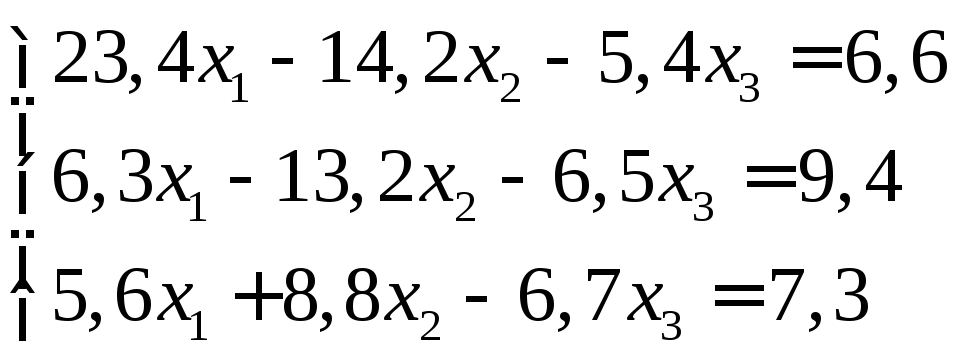 22.
22.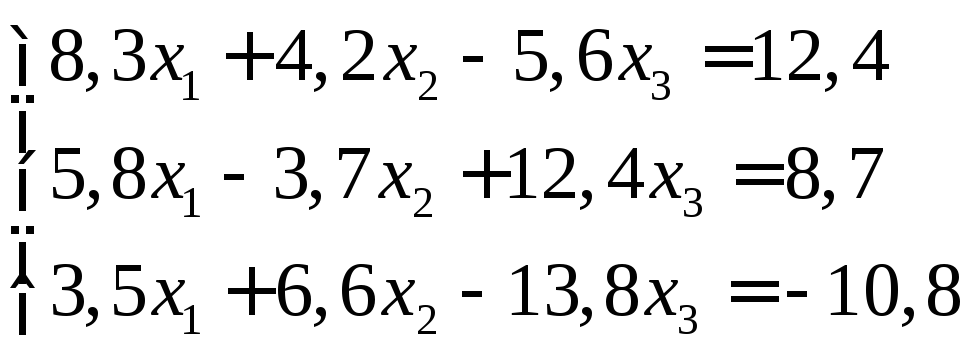
8.
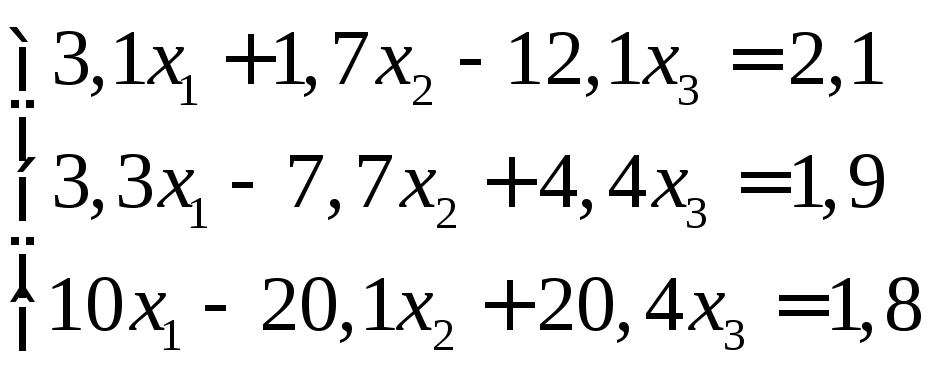 23.
23.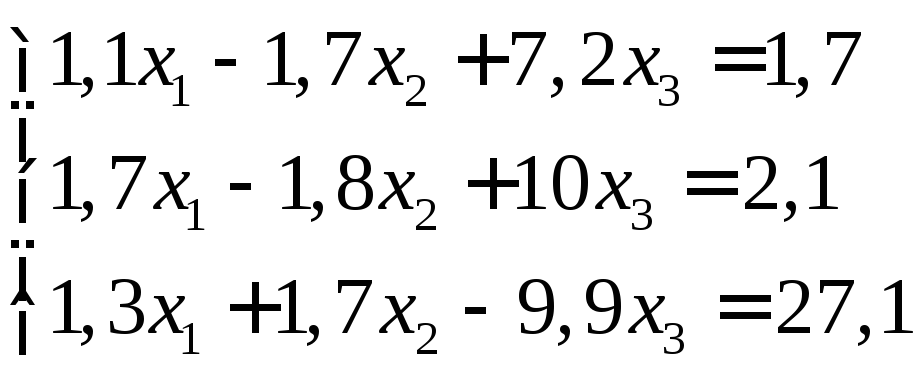
9.
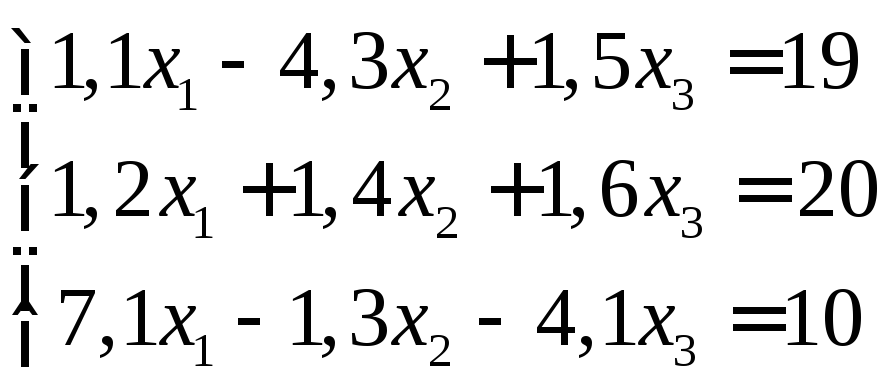 24.
24.
10.
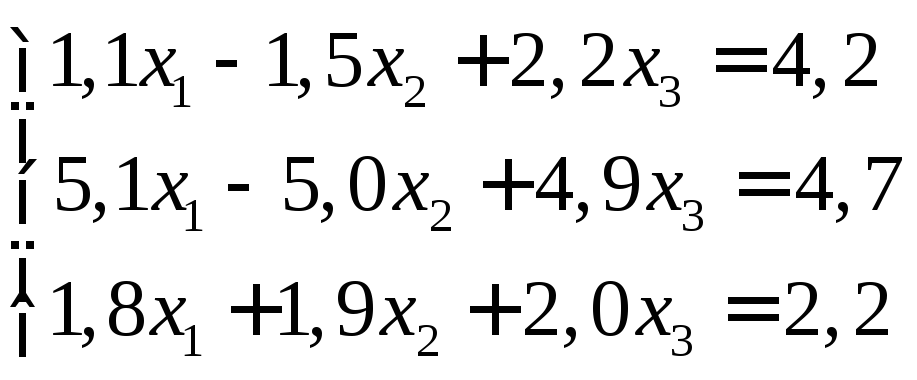 25.
25.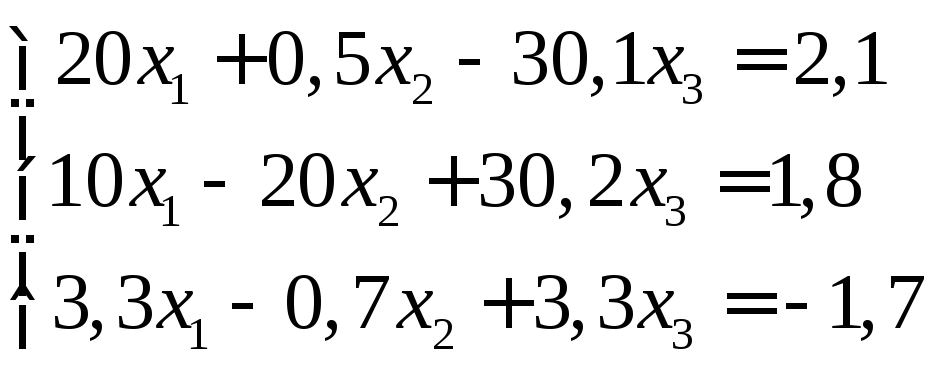
11.
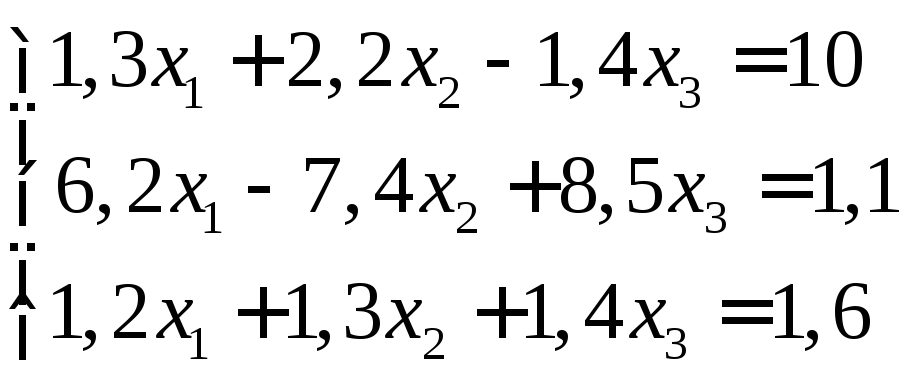 26.
26.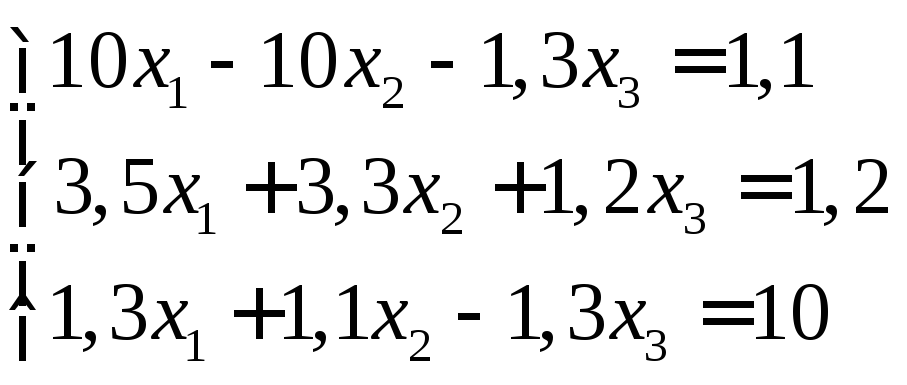
12.
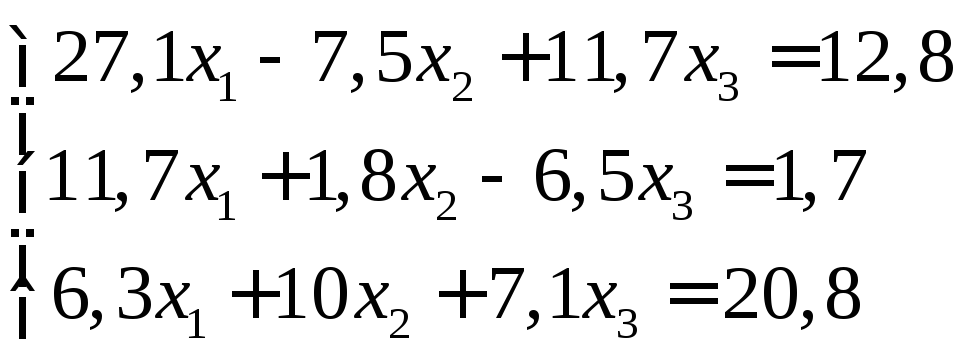 27.
27.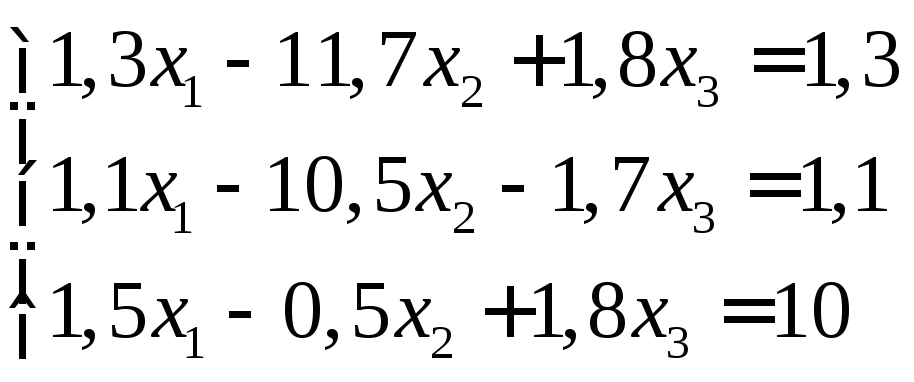
13.
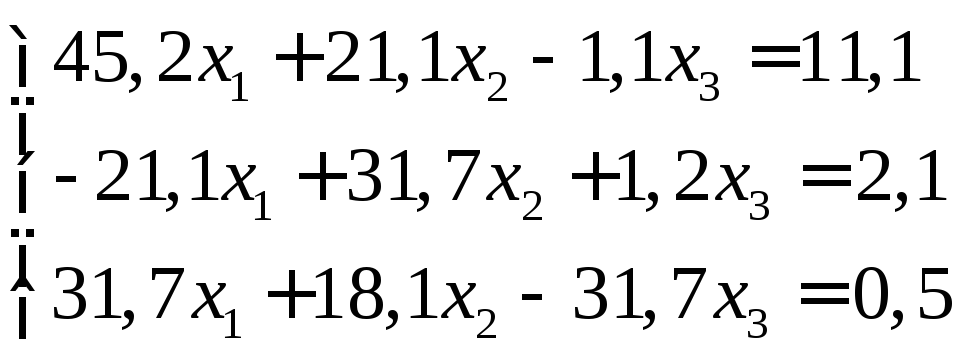 28.
28.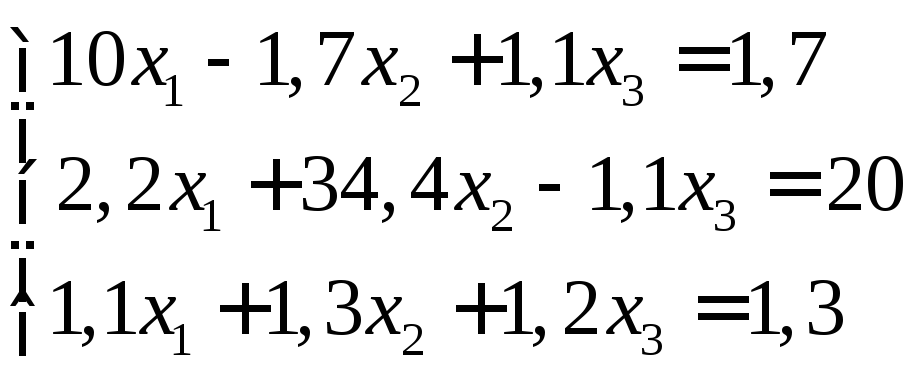
14.
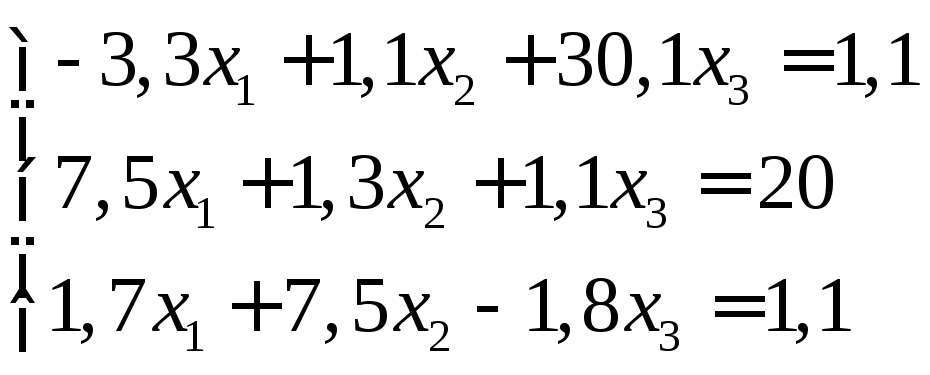 29.
29.
15.
 30.
30.