6.5. Операции с квадратными матрицами

Вначале подготовимся к работе. Образуйте матрицу размером 3×3: Она нам понадобится для освоения операций с квадратными матрицами.

		1	3		9				6.5.1. Определитель квадратной матрицы.
							Для вычисления определителя нужно ввести
	A :=	−7	6	11
							идентификатор матрицы (сама квадратная мат-
			4				рица должна быть определена на листе Mathcad
	0.7				5
	determinant :=				A		выше). Затем нужно нажать клавишу со значком
									(выше клавиши <Ctrl> справа). Идентифика-
	determinant = −175.7						тор матрицы окружат вертикальные линии. Если
							нажать клавишу < = >, то выведется значение
	Рис. 2.24. Определи-						определителя. Часто бывает удобно присвоить
	тель матрицы.						значение определителя некоторой переменной,

чтобы использовать ее в дальнейших вычислениях. Выполните упражнение, показанное на рис. 2.24.

Вычисление определителя изучено.

6.5.2. Длина вектора. Для вычисления длины вектора (квадратный корень из суммы квадратов всех его элементов) используется та же кла-

виша 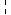, что и для вычисления определителя матрицы. Сделайте упражнение по рис. 2.25.

Определение длины изучено.

1

V := 23

4

dlina := V dlina = 5.477

VT V = ( 5.477)

Проверка: тот же результат должен получиться, если извлечь квадратный корень из скалярного произведения вектора самого на себя. Значок корня вводится клавишей < \ > (над клавишей Ctrl справа)

Мы снова видим особенность вывода результата скалярного произведения в формате 1×1

Рис. 2.25. Вычисление длины вектора.

6.5.3. Обращение квадратных матриц. Согласно аксиомам алгебры матриц обратной матрицей называется такая, результат умножения которой на исходную матрицу есть единичная матрица. Обращение матрицы возможно только в том случае, когда ее определитель не равен нулю

43

(в противном случае Mathcad выведет сообщение об ошибке). Для обращения матрицы нужно охватить идентификатор обращаемой матрицы синим контуром и нажать клавиши <Shift>+<6> (как для ввода степени). В слот нужно ввести степень -1.

Упражнение – в разделе 6.6.

Операция обращения матрицы изучена.

6.6. Решение примеров с действиями алгебры матриц

6.6.1. Решим пример 1, иллюстрирующий все изученные операции. Постановка задачи. Случается, что математический результат, полученный исходя из строгой формальной постановки задачи, не обладает прозрачностью, нужной для использования в инженерной практике. Так произошло с формулами, разработанными для выделения полезного сигнала из результатов измерения с помехами. Математический результат был получен

М. Аоки в форме матричного выражения ( A +	B R	− 1 B T ) − 1 .
n × n	n × m m	× m m × n

Здесь A – квадратная матрица размерности n×n, R – квадратная матрица размерности m×m, B – неквадратная матрица размерности n×m. На рис. 2.26 показан результат проверки соответствия размерностей.

−1

T

−1

До работ М. Аоки в инженер-

( A

ной практике уже использовались

+ B R

B

)

фильтры помех, но внешне струк-

n ×n

n ×

×

× n

тура известных фильтров не отве-

m m

m

m

Должны быть

чала

выведенному

матричному

уравнению. М. Аоки предположил,

одинаковыми

Размерность результата

что причина не в том, что синтези-

рованный им фильтр не сходен с из-

умножения n × n

вестным, а в том, что полученная им

формула имеет другое тождест-

Размерности сумми-

венное

представление,

отвечающее

руемых матриц

структуреинженерного фильтра.

должны совпадать

Для подтверждения этого пред-

Рис. 2.26. Проверка размерностей.

положения было использовано спе-

циальноематричноетождество.

(A + B R− 1 BT)− 1

A− 1 − A− 1 B (BT A− 1 B + R)− 1 BT A− 1

Замечание: представляет интерес – каким же образом автор тождества додумался до получения такой огромной формулы (ведь тождества не доказываются, а лишь проверяются, поэтому их можно только придумать, а не вывести из теорем). Скорее всего, автор руководствовался стремлением согласовать формулу с инженерными интуитивными выводами. Для этого нужно было выделить A-1 в качестве вычитаемого. Если все величины – скаляры, такое выделение получается элементарно. После этого остается переписать формулу со скалярами в матричную формулуссоблюдениемразмерностейиполучитьтождествокакновыйнаучныйрезультат.

44

Решение примера. Выполните проверку этого тождества по рис. 2.27. В ходе проверки закрепите все знания по матричной алгебре, полученные в ходе лабораторной работы. При расчетах с другой матрицей R используйте правила размерностей при сложении и умножении матриц.

Сформируйте исходные данные:

13	1	−200		B := −7	2	0.5		A := 0.5				0
R := 0	19	1
	0.3	0.9		11	0.1	3				0	0.4
0.1
Вычислите		(A + B R− 1 BT)− 1
Должно получиться								1.286			0.8
								−0.185		−0.11
Вычислите		A− 1 − A− 1 B (BT A− 1 B + R)− 1 BT A− 1
Должно получиться				1.286	0.8
				−0.185 −0.11
								1	−200		1
Вставьте столбец и строку						13
					R :=		0	19	1		−7
в матрицу R, чтобы получилось:
								0.3	0.9		8
						0.1
							3	9	23		19

Внесите исправления в другие исходные данные, чтобы расчеты стали возможными.

Рис. 2.27. Контрольные примеры.

6.6.2. Составьте сами примеры, иллюстрирующие аксиомы и теоремы алгебры матриц (по таблице заданий). При составлении примеров используйте размерности не ниже 3 и соблюдайте правила согласования размерностей при сложении и умножении матриц.

Таблица заданий для разработки иллюстративных примеров.

Замечание: в строках таблицы использованы одни и те же обозначения (A, B, C), но это не означает, что в примерах должны быть использованы одинаковые матрицы для всех формул (нужно каждый раз переопределять матрицы, чтобы соблюдалось согласование размерностей).

Составленные примеры покажите преподавателю. Постарайтесь за-

45

помнить формулы, приведенные в табл. 1, они многократно Вам понадобятся при изучении самых разных дисциплин.

					Таблица 1
	№	Аксиомы и теоремы теории	Примечания
		матриц
	1.	(A B)T = BT AT	A, B – прямоугольные матрицы со-
			гласованных	размерностей. Для
			ввода знака	транспонирования –
			клавиши <Ctrl>+<1>.
	2.	(A B)–1 = B–1 A–1	A, B – квадратные матрицы, опре-
			делители которых не равны 0
	3.	A + (B + C) = (A + B) + C =	A, B, C – прямоугольные матрицы
		= A + B + C	согласованных размерностей
	4.	A (B + C) = A B + A C	--------«»--------
	5.	A (B C) = (A B) C = A B C	--------«»--------
	6.	AT A – симметричная матрица	A – прямоугольная матрица произ-
			вольной размерности
	7.	aT b = bT a: скалярное произ-	a, b – векторы одинаковой размер-
		ведение переместительно	ности.
		6.7. Специальные приемы работы с матрицами
		6.7.1. Собственные числа квадратной матрицы. Как известно,
собственные (иначе – характеристические) числа λi,					i = 1, … , n, квад-
ратной n×n матрицы A являются корнями уравнения					det(A −λ E) = 0 ,

где λ – вектор собственных чисел с компонентами λi, i = 1, … , n, E – единичная n×n матрица, det( ) – определитель.

В Mathcad имеется встроенная функция eigenvals( ), возвращающая вектор собственных чисел. Испытайте эту функцию по рис. 2.28. Обратите внимание на небольшие неточности решения уравнения для собственных чисел. Конечно, они настолько малы, что не сказываются на качестве расчетов.

46

	13		1	−200	1		Вектор собственных чисел
		0	19	1	−7
R :=								матрицы R:
		0.1	0.3	0.9	8			λ := eigenvals (R)
		3	9	23
					19				−10.573
Собственные числа (два действительных								λ =	22.418+ 12.798i
и два комплексно сопряженных)
									22.418− 12.798i
									17.637

Проверка на соответствие уравнению для собственных чисел:

i := 0.. rows(R) − 1	verify :=		R − λi identity(rows(R))
	i

Уравнение удовлетворяет с очень малой погрешностью (порядка 10-11)

				− 12
			−8.356× 10
			− 11	− 11
	verify =		−3.325× 10	− 2.981i× 10
			− 11	− 11
			−3.325× 10	+ 2.981i× 10
				− 12
			1.448× 10

Рис. 2.28. Собственные числа матрицы.

6.7.2. Характеристические векторы квадратной матрицы. Как известно, квадратная n×n матрица A имеет n характеристических векторов. Умножение матрицы на вектор приводит к получению нового вектора, направление которого в общем случае отличается от направления век- тора-сомножителя. Характеристические векторы составляют исключение из этого правила: умножение матрицы на них приводит к получению векторов, совпадающих с ними по направлению, т. е. характеристические векторы удовлетворяют уравнению: A vi = λi vi , i = 1, … , n, λi – i-е

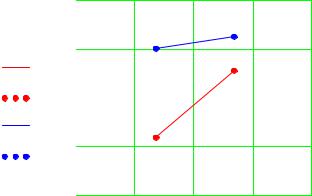
собственное число (см. п. 6.7.1). В Mathcad имеется встроенная функция eigenvecs( ), возвращающая матрицу, каждый столбец которой является характеристическим вектором матрицы, указанной в качестве аргумента функции eigenvecs( ). Характеристические векторы выводятся нормированными, т. е. имеющими единичную длину (рис. 2.29).

47

	H :=				0	1
					0.9	0.5
	λ := eigenvals (H)
	z := eigenvecs (H)
	z =		0.807					0.63
			−0.59			0.776
	v1 := z 0					v2 := z 1
		v1		= 1				v2		= 1

–квадратная матрица, характеристические векторы которой нужно найти

–собственные числа матрицы H

–матрица, столбцы которой – характеристические векторы

–значения элементов векторов

–каждому вектору можно присвоить отдельный идентификатор (вырезывание столбца матрицы – клавишами <Ctrl>+<^>))

–характеристические векторы нормированны: их длина равна 1 (для определения длины нажмите клавишу < | > )

Для вывода векторов на график задайте
индекс размерностей:										j := 0.. 1
									1.5										График		иллюстрирует
λ0 v1j				0.75															совпадение
																			характеристических
(H v1) j																			векторов с результатами
																			их поворота матрицей H
λ1 v2j
		1					0.25							0.5			1.25					2
(H v2) j					0.75
								1.5

j

Рис. 2.29. Характеристические векторы.

48

Научимся выводить векторы на график. Нужно выполнить следующие операции:

Задать диапазон изменения индексов элементов вектора (в примере на рис. 2.29 вектора двумерны, соответственно индекс изменяется от 0 до 1).

Вывести шаблон графика (<Shift>+<2>) и на оси абсцисс указать имя индекса (в примере j).

Указать на оси ординат идентификатор элемента вектора с индексом таким, как на оси абсцисс (в примере j).

В результате выведется вектор.

Сделайте упражнение по рис. 2.29 и убедитесь, что действительно поворот характеристического вектора матрицей приводит к получению вектора, накладывающегося на сам характеристический вектор.

Изучение собственных чисел и характеристических векторов закон-

чено.

6.7.3. Диагонализация квадратных матриц. Как известно, квадрат-

ную матрицу можно привести к диагональной форме, причем в диагонали располагаются собственные числа этой матрицы. Приведение к диагональной форме бывает полезным для того, чтобы упростить операции умножения (Вы знаете, что умножение на диагональную матрицу не вызывает затруднений).

Рассмотрим пример. Пусть задана матрица R размерности 4×4 и требуется возвести ее в 100-ю степень. Если мы будем использовать длинную операцию умножения R R… R, используя правила умножения матриц, то, скорее всего, в среде Mathcad никогда не досчитаем до результата. Однако Mathcad выводит результат почти мгновенно. Используется алгоритм, показанный на рис. 2.30. Выполните показанные там вычисления.

49

13

1

−200 1

Пусть задана квадратная матрица:

R :=

0

19

1

−7

0.1

0.3

0.9

8

Требуется вычислить Rn, n = 100

3

9

23

19

АЛГОРИТМ:

−10.573

1. Вычисляем вектор собственных чисел:

22.418+ 12.798i

λ := eigenvals(R)

λ =

22.418− 12.798i

2. Вычисляем матрицу

характеристических векторов:

17.637

T := eigenvecs(R)

3. Приводим матрицу R к диагональной форме (в диагонали получатся собст-

венные числа):

−10.573

−0 + 0i

−0 − 0i

0

Λ := T

-1

R T

Λ =

−0 − 0i

22.418+ 12.798i

−0 + 0i

0

(имеются небольшие

−0 + 0i

−0i

22.418− 12.798i

0

вычислительные

погрешности порядка 10-15)

−0

0

0

17.637

4.Вводим степень, в которую нужно возвести матрицу R: n := 100

5.Рассчитываем диагональную матрицу, в диагонали которой – степени собственных чисел:

Λn := diag( λn )

6.Используем обратное преобразование из диагональной матрицы в Rn: Rn := T Λn T-1

7.Выводим результат на экран: Rn =

8.Для проверки вычисляем непосредственно: Rn =

Рис. 2.30. Диагонализация квадратных матриц.

Убедитесь, что матрицы R и Rn имеют одинаковый набор характеристических векторов при любом показателе степени n. Объясните, почему.

Изучение процесса диагонализации квадратных матриц закончено.

6.7.4. Свойства симметричных матриц. Симметричные матрицы,

т. е. такие, в которых совпадают элементы, симметрично расположенные относительно главной диагонали, имеют много интересных свойств, часто используемых на практике. Выполните упражнение, показанное на рис. 2.31, и постарайтесь запомнить свойства симметричных матриц.

50

						1			3		4		7
						3		11			2		−5
	Введем симметричную матрицу А:			A :=			4		2	−19			−8
	ИЛЛЮСТРАЦИИ свойств					7		−5			−8		9
	симметричных матриц:									0		0	0	0
											0	0	0	0
	1. Матрица и транспонированная к ней равны:						T
					A − A				=		0	0	0	0
				10.195							0	0	0
	2. Собственные числа симметричной													0
				16.732
	матрицы – ВЕЩЕСТВЕННЫ:	λ =
	λ := eigenvals(R)			−2.378
	3. Характеристические векторы			−22.549							−0.164			−0.768				0.245
	симметричной матрицы ВЕЩЕСТВЕННЫ:				0.569
	T := eigenvecs(R)				0.687						0.624			0.372				−0.01
	T =
				1.033× 10− 3							0.183			−0.333 −0.925
					0.452						−0.741			0.401				−0.29
	4. Транспонированная матрица,						0		0		0	0
					− 1		0		0		0	0
	составленная из характеристических	T	−			=
	векторов, равна обратной матрице	T		T				0	0		0	0
	характеристических векторов:								0		0
							0					0
	5. Диагонализация симметричной матрицы					10.195					0			−0				0
	проводится по формуле:							0		16.732				0				−0
	T
	DiagA := T A T	Diag_A =					−0				0		−2.378					−0
								0			−0			−0 −22.549

Рис. 2.31. Свойства симметричных матриц.

Изучение свойств симметричных матриц закончено.

6.7.5. Квадратичные формы. Как известно, квадратичной формой

	Симметричная	называется	скаляр,	структура
		которого показана на рис. 2.32.
	Транспонированный матрица Вектор
	вектор-строка	Если развернуть этот скаляр в
		виде сумм и произведений, то
	xT Q x
		мы увидим, что в формулу
	1×n n×n n×1	войдут в	качестве	слагаемых
		квадраты	каждого	элемента
	Размерность результата	вектора x и перекрестные про-
	1×1 = скаляр	изведения одних элементов на
	Рис. 2.32. Структура квадратичной формы.	другие. Коэффициентами при
	51

этих слагаемых будут элементы симметричной матрицы, которая, как Вы знаете, называется ядром квадратичной формы.

Проиллюстрируем графически свойства квадратичной формы (Вы неоднократно встретите квадратичные формы в самых различных учебных дисциплинах).

Вначале научимся выполнять матричные преобразования в режиме live symbolic (см. Часть 4). Символьные преобразования с матрицами можно делать при не слишком высокой размерности (иначе формулы получались бы совершенно необозримыми). Для наших целей достаточно размерности ядра квадратичной формы 2×2 (соответственно вектор x будет иметь 2 элемента). Набираем по рис. 2.33:

Набор <Ctrl>+<1> 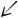(транспонирование)

x1 T q11				q12			x1
x		q	21	q	22		x		→
2							2

Вызов шаблонов матриц и векторов <Ctrl>+<М>

В результате получится:

x1 T q11				q12 x1
x		q	21	q	22		x
2							2

Набор <Ctrl>+<Shift>+<точка> (символический знак присваивания)

→ (x1 q11 + x2 q21) x1 + (x1 q12 + x2 q22) x2

Скопируйте результат и упростите:
(x 1 q 11 + x 2 q 21) x1 + (x 1 q 12 + x 2 q 22) x 2 simplify								→							2
х	2	2		+ х ·х ·q + х ·х ·q + х								2	·q
	1x	·q														q
→		1	11q	11	+1	x2 x12 q		21	+1 x 21x		q2	12		22+ x	2		2
						1	2			2	1
Получим формулу квадратичной формы в скалярах:

f(x1,x2,q 11,q 12,q 22):= x 12 q 11 + 2 x1 x2 q 12 + x 22 q 22

Рис. 2.33. Запись квадратичной формы в скалярах.

В зависимости от состава собственных чисел матрицы Q значение функции 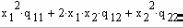может оказаться таким, что:

При любых значениях элементов вектора x значение функции положительно. Соответствующая квадратичная форма называется положительно определенной. Собственные числа ее ядра положительны (и, конечно, действительны, т. к. Q – симметричная матрица).

52

При любых значениях элементов вектора x значение функции отрицательно. Соответствующая квадратичная форма называется отрицательно определенной. Собственные числа ее ядра отрицательны (и, конечно, действительны).

При некоторых значениях элементов вектора x значение функции

положительно, а при других – отрицательно.

Рассмотрим пример для всех трех случаев и проиллюстрируем его графиками. Сделайте вычисления и построения, показанные на рис. 2.34.

Введем 3 матрицы: Значения элементов:

Q1 :=

5

3

q11

5,q12

3,q22

9

3

9

Q2 := −Q1

q11

−5,q12

−3,q22

−9

Q3 :=

−2

3

q11

−2,q12

3,q22

1

3

1

Определим состав собственных чисел:

eigenvals (Q1) =

3.394

- все положительны

10.606

eigenvals (Q2) =

−3.394

- все отрицательны

−10.606

eigenvals (Q3) =

−3.854

- одно отрицательное, другое положительное

2.854

Квадратичная форма в скалярах:

2

2

q22

f(x1,x2,q11,q12,q22):= x1 q11 + 2 x1 x2 q12 +

x2

Построим график функции f(...) на интервале изменения x1 и x2 от -0.15 до +0.15

Число точек на каждой оси графика - по 20.

Индексы точек: i := 0.. 20							j := 0.. 20
Координаты аргументов соответствующие индексам:
x1 := −0.15 + 0.015 i						x2	:= −0.15 + 0.015 j
i							j
	Массивы для вывода трехмерных графиков:
F1	:= f x1		,x2		,5,3,9		- для ядра квадратичной формы Q1
i, j		i	,x2	j
F2	:= f x1				,−5,−3,−9 - для ядра квадратичной формы Q2
i, j		i	,x2	j	,−2,3,1
F3	:= f x1						- для ядра квадратичной формы Q3
i, j		i		j

Рис. 2.34. Подготовка к выводу графических образов квадратичных форм.

Теперь вызовите шаблон трехмерного графика (<Ctrl>+<2>) и в появившийся слот впишите имя массива F1. Затем выведите такие же графики и для других массивов. Получится так, как на рис. 2.35.

53