В матрично-векторных обозначениях (с учетом MathCAD-нумерации элементов матриц с нуля) система уравнений имеет вид:

A(t)0,0 x(t)0 +	A(t)0,1 x(t)1		B(t)0
A(t)1,0 x(t)0 +	A(t)1,1 x(t)1		B(t)1

Введем вектор искомых переменных(жирный знак равенства <Ctrl>+<=> исключает вычисления):

		x(t)	0
x(t)
		x(t)
			1

Элементы матриц A(t) и B(t) найдены ранее в процессе векторизации, рис. 4.37

		A(t)	0,0	A(t)	0	,1				B(t)	0
A(t)								B(t)
		A(t)	1,0	A(t)	1	,1				B(t)
											1

Решение системы уравнений в матрицах:

x(t) := A(t)− 1 B(t)

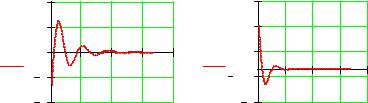
Исследование решения по графику. Задаем диапазон изменения параметра t: t := 0,0.001.. 5

Выводим графики элементов вектора x(t) (для получения шаблона графика нажмите <Shift>+<2>)

	2					2
	1					1.25
x(t)0	0	1.5	3	4.5	x(t)1	0.5
					6
	1					0.25	0	1.5	3	4.5	6
	2					1
			t						t

Рис. 2.38. Решение системы линейных уравнений с помощью матриц.

7.3. Применение матриц и векторов в задаче интерполяции

7.3.1. Необходимые теоретические сведения. Интерполяцией на-

зывается группа методов восстановления значений функции в промежутках между точками, заданными своими координатами.

Реализуем с помощью матрично-векторных операций один из наиболее применяемых методов интерполяции – интерполяция с помощью так называемых кубических сплайнов. Сплайны широко используются в компьютерной технике (компьютерной графике, компьютерном черчении, компьютерной фотографии).

58

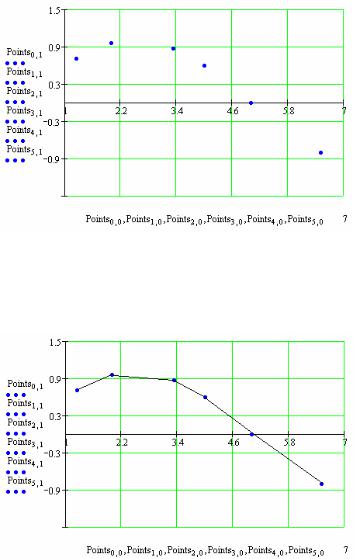
ДАНО: координаты точек (рис. 2.39).

ПОЛУЧИТЬ: уравнение гладкой кривой, которая проходит через все заданные точки. Такая кривая позволяет вычислить значение функции между заданными точками – т. е. решить задачу интерполяции.

Рис. 2.39. Точки, через которые должна пройти интерполяционная кривая.

Если просто соединить точки участками прямых линий, то получится ломаная линия – так называемая кусочно-линейная интерполяция (иначе – сплайн первого порядка). Она непрерывна, но ее производные (начиная с первой) разрывны, поэтому ломаная линия не кажется нам гладкой (рис. 2.40).

Рис. 2.40. Интерполяция сплайном первого порядка.

59

В результате многолетних исследований особенностей восприятия зрительных образов человеком было установлено, что кривая воспринимается как вполне гладкая, если она сама и две первые ее производные непрерывны. Так пришли к идее кубических сплайнов – когда точки соединяются участками кубических парабол.

Примечание: слово «сплайн» в переводе с английского языка означает гибкую металлическую линейку, которую чертежники 19-го века изгибали для плавного соединения точек. Термин «кубический» ассоциируется с кубической зависимостью. Другое название - кубического сплайна – сплайн третьего порядка (если для интерполяции использовать обычные параболы, получится сплайн второго порядка, а если прямые, как на рис. 2.40 – сплайн первого порядка).

Основная идея интерполяции кубическими сплайнами:

Кубическая парабола y(x) = a	0	x3 + a x2	+ a	2	x + a	3	содержит 4
		1

коэффициента ai, i = 0, … , 3, поэтому если взять 4 значения аргумента xi подряд, i = 1, 2, 3, 4 и соответствующие им значения функции y(xi), то по этим данным можно рассчитать все ai, i = 0, … , 3. Тогда, если построить график функции y(x), то он пройдет точно через эти точки. В промежутках между точками можно будет рассчитать значение функции для любого аргумента, используя формулу кубической параболы.

Обычно точек гораздо больше, чем 4. Тогда поступим так: будем строить для каждых 4-х точек свою кубическую параболу – аналогично тому, как мы строили свою прямую линию для каждых двух точек при аппроксимации первого порядка, см. рис. 2.40. В узлах сопряжения двух соседних кубических парабол значения функции и первых двух производных окажутся равными, в результате чего кривая, составленная из участков кубических парабол с разными коэффициентами, будет восприниматься глазом как гладкая.

Опишем последовательность шагов для получения интерполяционной кривой, построенной на кубических сплайнах.

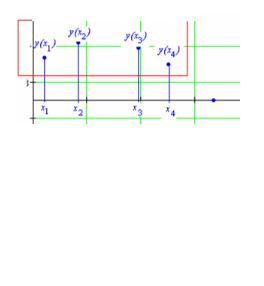
Шаг 1. Берем координаты первых четырех точек, охватываем их окном (рис. 2.41). Составляем систему уравнений для определения коэффициентов ai, i = 0, … , 3, решаем ее и получаем уравнение кубической параболы. Система уравнений имеет вид, показанный на рис. 2.41.

Шаг 2. Используя найденные на шаге 1 значения коэффициентов ai, i = 0, … , 3, можно построить график функции y(x) = a0 x3 + a1 x2 + a2 x + a3 на интервале изменения аргумента x1 ≤ x ≤ x4 (рис. 2.42).

Шаг 3. Но для интерполяции функции используем не весь график для интервала x1≤ x ≤ x4, а лишь его фрагмент между точками x2 и x3, т. е. прорисовываем кубическую параболу y(x) = a0 x3 + a1 x2 + a2 x + a3 только на интервале изменения аргумента x2 ≤ x ≤ x3 (см. рис. 2.42).

60

Окно захвата точек для сплайна

Система уравнений для определения коэффициентов кубической параболы:

	3	a0		2	a1	1	a2		0	a3		= y(x1 )
x1				+ x1		+ x1			+ x1
x3		a	0	+ x2	a	+ x1	a	2	+ x0	a	3	= y(x	2	)
	2			2	1	2			2
x3		a	0	+ x2	a	+ x1	a	2	+ x0	a	3	= y(x	3	)
	3			3	1	3			3
x3		a	0	+ x2	a	+ x1	a	2	+ x0	a	3	= y(x	4	)
	4			4	1	4			4

В этой системе уравнений неизвестные: a0, a1, a2, a3

Известные: xi, y(xi), i = 1, 2, 3, 4

Рис. 2.41. Иллюстрация к построению сплайна.

Шаг 4. Далее сдвигаем окно, в которое попадают точки интерполируемой кривой, на одну точку (рис. 2.43). Мы видим, что точка с абсциссой x1 в «новое» окно не попала; точки x2, x3 и x4 из «старого» окна перекочевали в новое, а точка с абсциссой x5, появившаяся в «новом» окне, «старым» окном не охватывалась. Теперь, если мы рассчитаем значения коэффициентов ai, i = 0, … , 3 по координатам точек «нового» окна (x2, x3, x4 и x5), то получим другую кубическую параболу (но отличающуюся от первой не слишком сильно, т.к. обе они должны пройти через общие для обоих окон точки x2, x3 и x4), рис. 2.44.

Шаг 5. Теперь прорисуем второй участок интерполирующей кривой по уравнению второй параболы, коэффициенты которой рассчитаны для аргументов «нового» окна x2, x3, x4 и x5. Мы видим (рис. 2.45), что участки примыкают друг к другу гладко, без разрывов. Можно показать, что в точке сопряжения участков (ее абсцисса равна x3) у обеих парабол одинаковы значения самих функций и их производных первого и второго порядков.

61

Рис. 2.42. Иллюстрация к шагу 3: прорисовка первого фрагмента интерполирующей функции.

Рис. 2.43. Иллюстрация к шагу 4: точки для построения второй кубической параболы.

Последующие шаги выполняются в цикле, начиная с шага 4: последовательно сдвигаем окно, в которое попадают очередные 4 точки; по их координатам вычисляем коэффициенты соответствующей кубической параболы; прорисовываем эту параболу между второй и третьей точкой окна. Так получим кривую, плавно соединяющую точки, начиная со второй и заканчивая предпоследней.

62

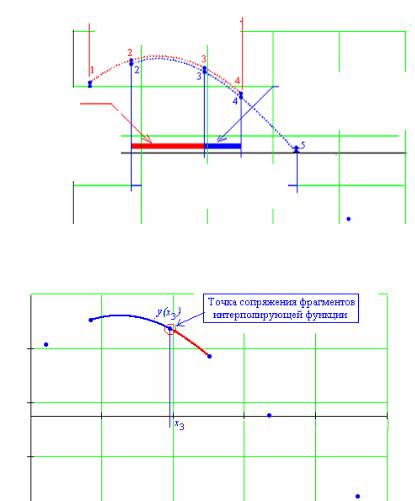
Точки, по которым вычислены коэффициенты для первой кубической параболы

Область аргументов для вычисления интерполирующей функции: по уравнению первой па-

раболы Точки, по которым вычислены коэффициенты для второй

кубической параболы

Область аргументов для вычисления интерполирующей функции: по уравнению второй параболы

Рис. 2.44. Иллюстрация к шагам 4 и 5: построены две кубические параболы. Первая – по точкам 1,2,3,4. Вторая – по точкам 2,3,4,5.

Показаны области определения аргументов для построения интерполирующей кривой.

Рис. 2.45. Иллюстрация к шагу 5: два фрагмента интерполирующей функции. Первый – участок кубической параболы, коэффициенты которой рассчитаны

по точкам 1,2,3,4. Второй – участок кубической параболы, коэффициенты которой рассчитаны по точкам 2,3,4,5.

Первый и последний участки (от первой до второй точки и от предпоследней, N–1-й, до последней, N-й точки) оказываются не охваченными интерполяционной функцией. Имеются разные варианты обхода этого недостатка. Первый – просто отбросить первую и последнюю

63

точки. Область интерполяции будет уже области, занятой точками, но если точек много, то это может оказаться несущественным. Второй – дополнить первый и последний участок либо прямыми линиями, либо параболами. Можно также продлить участки прорисовки первой и последней кубических парабол (первую использовать для интерполяции не только между точками 2 и 3, но также и между точками 1 и 2; последнюю – для интерполяции между точками N-2 и N-1, но и между точками N-1, N).

7.3.2. Решение задачи интерполяции функции в среде Mathcad с использованием матриц и векторов.

ДАНО: координаты точек в форме файла Data.txt. Файл нужно скопировать в текущий каталог студента, чтобы для чтения файла не нужно было указывать путь к нему. Структура файла (просмотрите ее средствами оболочки операционной системы): первый столбец – значения абсцисс точек, второй – значения ординат точек.

ПОЛУЧИТЬ: гладкую кривую, соединяющую точки. Решение проводится поэтапно.

Этап 1. Чтение файла с диска, определение числа точек, вывод точек на график.

Этап 2. Расчет параметров кубических парабол для интерполирующей функции.

Этап 3. Указание интервалов изменения абсциссы для каждой кубической параболы.

Этап 4. Построение интерполирующей кривой.

7.3.2.1. Выполнение этапа 1: «Чтение файла с диска, определение числа точек, вывод точек на график».

а) Выбираем идентификатор массива (например, Points) и считываем файл с координатами точек в этот массив:

Points := READPRN(“Data.txt”).

б) Определяем число точек (m) в массиве (по числу строк) с использованием функции rows( ):

m := rows(Points)

Выводим значение m:

m = 6

в) Учитывая нумерацию элементов массива в Mathcad с нуля, вводим индексы точек:

k := 0 .. m-1

г) Для того чтобы избежать громоздких обозначений, вводим раздельные идентификаторы для абсцисс (xk) и ординат (yk) точек:

x := Points 0	y := Points	1
		.

64

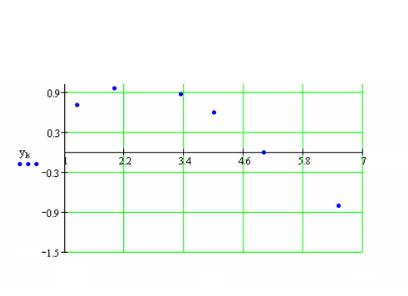
Для слота номера столбца используйте клавиши <Ctrl>+<6>.

д) Выводим точки на график, чтобы наглядно представить себе их расположение. Используем шаблон графика (<Shift>+<2>) и указываем абсциссыиординатыточек. Должно получитьсятак, какпоказанонарис. 2.46.

Для того чтобы показать точки, щелкните левой кнопкой мыши по области графика, выберите вкладку Trace (линии) и укажите тип (Type) Points (точки). Укажите для них толщину (Weight) 3 и одинаковый цвет (Color). Затем выберите вкладку XY-axes (оси), включите линии сетки (Grid lines), отключите автоматическое определение числа точек (AutoGrid) и введите по 5 линий сетки на осях X и Y. Затем введите русский стиль осей

(Axes Style) – пересечение (Crossed).

хк

Рис. 2.46. Исходные данные для построения интерполяционной функции.

Этап 1 завершен.

7.3.2.2. Выполнение этапа 2: «Расчет параметров кубических парабол для интерполирующей функции». Пусть в окно, охватывающее очередные 4 точки для построения фрагмента интерполирующей функ-

ции, попали точки yk, yk+1, yk+2, yk+3 с абсциссами xk, xk+1, xk+2, xk+3, k = 0, 1, … , N–3, N – индекс последней точки,

N := m-1, N = 5.

По координатам этих точек нужно найти параметры k-й кубической параболы, проходящей через них. Уравнение параболы на участке xk ≤ x ≤ xk+3 имеет вид:

y = ak ,0 + ak ,1 x + ak ,2 x2 + ak ,3 x3 .

Исходя из того, что этому уравнению должны удовлетворять все точки yk, yk+1, yk+2, yk+3 , получим систему уравнений для определения парамет-

65

ров параболы:

	ak ,0 + ak ,1 xk + ak ,2 xk 2				+ ak ,3
		+ ak ,1 xk +1	+ ak ,2 xk +1	2	+ ak ,3
ak ,0
		+ ak ,1 xk +2	+ ak ,2 xk +2	2	+ ak ,3
ak ,0
		+ ak ,1 xk +3	+ ak ,2 xk +3	2	+ ak ,3
ak ,0

xk 3 = yk

xk +13 = yk +1

xk +2 3 = yk +2

xk +33 = yk +3

Введем матричные обозначения для этой системы уравнений:

	1	xk		xk		2
A		xk +1				2
	= 1			xk +1
k		xk +2				2
	1			xk +2
		x		x		2
	1		k +3
					k +3

xxk+33

xkk+123 xk +33

		yk
B	k	= yk +1
		yk +2
		yk +3

Тогда коэффициенты параболы найдутся так: ak = (Ak )−1 Bk ,

где ak – вектор коэффициентов параболы:

	ak ,0
	ak ,1
ak =	ak ,2	.
	ak ,3

Формула для интерполяции значений функции на интервале xk ≤ x ≤ xk+3 имеет вид:

f(ak,x) akT x,

где

1

x= xx2 .x3

Оформим эти вычисления в Mathcad (рис. 2.47).

66

Индексы элементов матриц А и В: i := 0.. 3 j := 0.. 3 k := 0.. N − 3

Матрицы, в которые входят все матрицы коэффициентов для всех кубических парабол:

Ai+k, j := (xi+k)j

Bi+k := yi+k

Числовые значения, которые должны получиться:

		1		1.25	1.563	1.953			0.707
			1	2	4	8				0.951
			1	3.333	11.109	37.026				0.866
	A =							B =
			1	4	16	64				0.588
			1	5	25	125				0
		1		6.5	42.25	274.625			−0.809

Вырезки матриц для каждой кубической параболы:

Ak,0 := submatrix(A ,k,k + 3,0,3) Bk := submatrix(B,k,k + 3,0,0)

Формула для расчета	Формула для интерполяции
параметров параболы:	значений функции:
	1
		z
ak := (Ak,0)− 1 Bk
	f(a,z) := aT	2
	z
	z3

Рис. 2.47. Формулы для расчета параметров кубической параболы.

Выполнение этапа 2 завершено.

7.3.2.3. Выполнение этапа 3: «Указание интервалов изменения абсциссы для каждой кубической параболы». Удобно указать вектор, эле-

ментами которого будут области определения абсцисс для каждой кубиче-

67

ской параболы. Это не совсем обычный вектор: значения его элементов – не числа, а числовые последовательности. Если попытаться его ввести как обычно (XXk := ), то Mathcad расшифрует это как команду вывода значений. Для того чтобы «обмануть» Mathcad, делайте так: сначала наберите

XX := xk+1,xk+1 + 0.01.. xk+2

(не обращайте внимание на «красный» сигнал об ошибке), а затем подставьте индекс под идентификатором XX скобкой < [ > ). Должно получиться так:

XXk := xk+1,xk+1 + 0.01.. xk+2

2,2.01.. 3.333

XX= 3.333,3.343.. 44,4.01.. 5

Мы видим, что каждый элемент вектора XX показывает, на каком интервале должны рассчитываться значения по соответствующей кубической параболе.

Как указывалось выше, для первого и последнего интервала нужно использовать дополнительные участки первой и последней кубической параболы. Соответствующие интервалы изменения аргументов:

Xstart := x0,x0 + 0.01.. x1 Xfinish := xN−1,xN−1 + 0.01.. xN.

Этап 3 завершен.

7.3.2.4. Выполнение этапа 4: «Построение интерполирующей кривой». Должно получиться так, как показано на рис. 2.48. Вы увидите гладкую кривую, соединяющую точки графика.

Выполнение этапа 4 завершено.

Решение задачи интерполирования значений функции закончено.

Нужно обратить внимание, что после соответствующей тренировки матрицы позволяют находить решение почти сразу: весь текст примера содержал только пояснения, а нужные расчеты «уложились» в показанные на рис. 2.47.

68