x0:= XX0	x1:= XX1		x2:= XX2
						k := 0.. N
	Начальный участок (рассчитан по пара-
	метрам первой кубической параболы)
						Участок, рассчитанный по параметрам
						первой кубической параболы
y k					1			Участок, рассчитанный по параметрам
f	(	a ,x0						второй кубической параболы
		0	)0						Участок, рассчитанный по па-
	(
f		a ,x1			0.5				раметрам третьей кубической
		1	)0						параболы
	(
f		a ,x2								Концевой участок (рас-
		2	)0
f(a0			,Xstart )0		1	2.2	3.4	4.6	5.8	считан по параметрам
										7
										последней кубической
f(a2			,Xfinish)							параболы)
				0	0.5
					1
						xk,x0,x1,x2,Xstart ,Xfinish
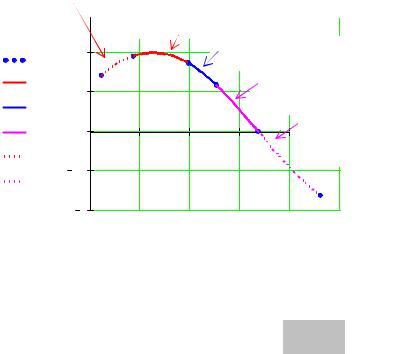
						Рис. 2.48. График интерполирующей функции.

Замечание: В одной из монографий по теории матриц в качестве эпиграфа было записано: «Матрицы экономят бумагу, но расходуют мозги». Монография устарела: после появления Mathcad матрицы экономят не только бумагу, но и мозги.

§8. Учебная задача

8.1. Постановка задачи

ДАНО: координаты вершин A, B, C, D параллелограмма (табл. 2). Ребра AB, AC, AD – смежные (т. е. выходят из одной вершины A).

Таблица 2

Таблица координат вершин:

Вершина A:	xA :=1	yA :=2	zA :=3
Вершина B:	xBB :=2	yB :=1	zB :=2
Вершина C:	xC :=3	yC :=3	zC :=1
Вершина D:	xD :=3	yD :=3	zD :=8

ПОЛУЧИТЬ:

1.Координаты остальных вершин параллелограмма;

2.Построить чертеж параллелограмма.

3.Найти длину ребер AB, GH.

4.Найти угол между ребрами AB и AC, сделать проверку.

69

5.Найти площадь грани, содержащей вершины A, B, C.

6.Найти объем параллелепипеда.

8.2.Решение

8.2.1. Пояснения к заданиям 1 и 2. Задания 1 и 2 выполняем параллельно, т. к. построение целесообразно делать по ходу нахождения координат вершин (иначе неизбежно запутаемся).

Этапы решения:

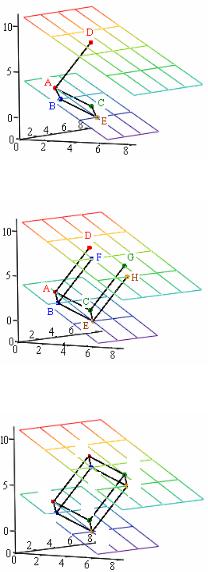
Этап1. СтроимплоскостьPABC, проходящуючерез3 вершины(A, B, C) параллелограмма. На этой плоскости разместится одна из граней параллелограмма. Способ построения плоскости по координатам 3-х точек подробно описан в учебной задаче к части 1 (§3).

Показываем на этой плоскости точки (вершины) (A, B, C) параллелограмма.

Получится так, как показано на рис. 2.49.

Рис. 2.49.

Этап 2. Строим плоскость PD, параллельную построенной на этапе 1 и проходящую через вершину D. На ней разместится грань параллелограмма, противоположная к находящейся на плоскости этапа 1.

Показываем на плоскости точку D. Получится так, как показано на рис.

2.50.

Рис. 2.50.

Этап 3. На плоскости PABC с вершинами A, B, C (этап 1) проводим отрезки прямых (ребра параллелограмма) AB, AC. Проводим отрезок прямой от точки A к точке D (ребро параллелограмма).

Получится так, как показано на рис. 2.51.

Рис. 2.51.

70

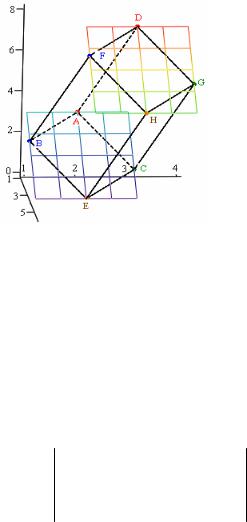
Этап 4. На плоскости PABC из вершины C строим отрезок, параллельный грани AB и равный ему по величине. Получаем координаты вершины E и грань СE.

Затем проводим отрезок, соединяющий вершины B и E тем же способом, что при выполнении этапа 3. Получаем грань BE. Этим завершается построение основания параллелепипеда.

Получится так, как показано на рис. 2.52.

Рис. 2.52.

Рис. 2.53.

D

G

F

H

A

C

B

E

Рис. 2.54.

Этап 5. Переходим к нахождению координат вершин на противоположной грани, располагаемой на плоскости PD. Одна из вершин задана (точка D в исходных данных). Используем ее для того чтобы аналогично этапу 3 провести отрезок, соединяющий заданные вершины A и D. Получаем ребро AD. Затем из точек B, C, E проводим отрезки такой же длины с таким же углом наклона, что и ребро AD. Получаем точки F, G, H и ребра BF, CG, EH. Получится так, как показано на рис. 2.53.

Этап 6. Соединяем отрезками прямых линий точки на плоскости PD, получаем ребра DG, GH, FH, DF. Построение параллелограмма завершено.

Получится так, как показано на рис. 2.54.

71

Этап 7. Расчет масштабов для плоскостей PABC и PD, соответствующих координатам вершин параллелограмма (этап выполняется для того чтобы чертеж выглядел профессионально). Невидимые ребра нужно показать пунктиром.

Получится так, как показано на рис. 2.55.

Рис. 2.55.

Указания к выполнению этапа 1 «Построение плоскости PABC,

проходящей через 3 вершины (A, B, C) параллелограмма, показ вершин A,

B, C». Подробное описание см. в Учебной задаче к части 1 (§3). Кратко: 1. Формируем определитель (сначала формируется матрица 3×3, <Ctrl>+<M>, затем в ее слоты вписываются нужные данные, затем матрицу нужно охватить синим контуром и набрать знак определителя | ) на основе координат вершин A, B, C. Приравниваем определитель нулю и решаем полученное уравнение относительно координаты z. Для вычисления используем символьные преобразования (<Ctrl>+<Shift>+<точка>, в слот вставляем команду solve (реши) и через запятую имя переменной, относительно которой ищется решение, т. е. z). НЕ ЗАБУДЬТЕ! Знак равенст-

ва ЖИРНЫЙ (<Ctrl>+<=>). Получится так:

x − x A				y − y A				z − z A
		− x		y		− y		z		− z
x	B		A		B		A		B		A
x C − x A				y C − y A				z C − z A

0 solve ,z → −x + 4

(т. е. уравнение плоскости PABC имеет вид z = – x + 4).

2. Формируем вектор 3×1 для координат плоскости, подлежащих выводу на график. Затем, используя функцию CreateMesh( ), вводим диапазоны аргументов x и y и частоту сеток. Поскольку до окончания расчета координат вершин параллелограмма нужный диапазон точно не известен, принимаем его на основании исходных данных «с запасом». Получится так:

72

		x
		y
PlaneABC(x,y) :=					Минимальное и максимальное
		−x + 4				значение аргумента y
PABC := CreateMesh (PlaneABC,0,6,0,6,4,4)
	Минимальное и максимальное						Число линий сетки
	значение аргумента x						по аргументам х и y

3. Формируем векторы из координат вершин A,B,C, D (это нужно для того, чтобы их легко было вывести на чертеж). В обозначениях Point- A, PointB, PointC, PointD использована «косметическая» (т. е. не индекс, а просто украшение текста, чтобы не писать PointA) точка (набирается, например, так: Point <точка> A).

xA		xB		xC		xD
PointA(x,y) := yA		PointB(x,y) := yB		PointC(x,y) := yC		PointD(x,y) := yD
z		z		z		z
A		B		C		D

4. Подготавливаем данные для вывода точек на чертеж (число линий сетки можно не указывать, т. к. точка – не объемная фигура. Это проявляется в том, что начальные и конечные значения аргументов записываются одинаковыми). В обозначениях использована «косметическая» точка:

TA := CreateMesh (PointA ,xA ,xA ,yA ,yA)

TB := CreateMesh (PointB,xB,xB,yB,yB)

TC := CreateMesh (PointC,xC,xC,yC,yC)

TD := CreateMesh (PointD,xD,xD,yD,yD)

5. Выводим шаблон пространственного графика (<Ctrl>+<2>), в слотах через запятые указываем идентификаторы плоскости и точек. Без настройки опций чертежа точки не будут видны. Для того чтобы показать их, щелкните дважды левой кнопкой мыши по графику, в появившемся окне выберите для графиков (Plot) показа точек (Plot 2, Plot 3, Plot 4) вкладку Appearance (внешний вид). Включите кнопку Draw Points (рисовать точки), укажите ее форму (Symbol) в виде точки (dots), размер (Size) не менее 2 (иначе точка будет незаметна на чертеже) и цвет (Solid Color). Цвета для точек выберите разными, чтобы можно было легко разобрать, к какой из них (A, B или C) относится изображенная точка. Для красоты чертеж плоскости также сделайте цветным: вкладка Plot 1, кнопка

73

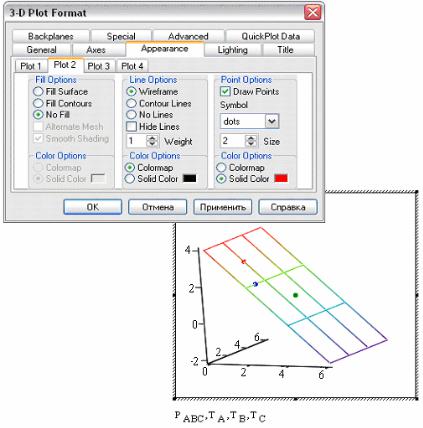
Color Map (Цветовая гамма), заполнение (Fill Options) – кнопка No Fill

(не заполнять, т. е. сделать чертеж плоскости прозрачным). Получим рис. 2.56:

Рис. 2.56.

Этап 1 завершен.

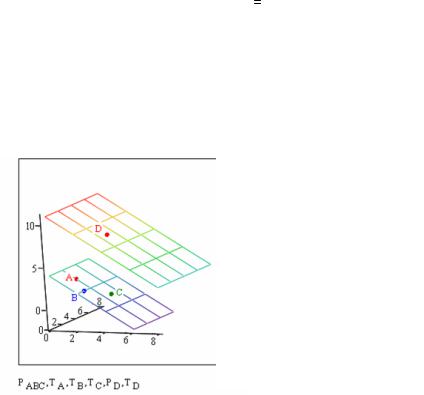
Указания к выполнению этапа 2 «Построение плоскости PD, па-

раллельной плоскости PABC, построенной на этапе 1; показ вершины D».

Формулы, позволяющие определить уравнение для плоскости, параллельной заданной и проходящей через заданную точку, приведены в Приложении 3. Последовательность действий:

74

1.Используем уравнение плоскости PABC, выведенное при выполнении этапа 1: z = – x + 4, см. п. 1 этапа 1. Сравниваем это уравнение со стандартным уравнением плоскости и определяем параметры стандартного уравнения:

Стандартное уравнение: P1·x + P2·y + P3·z + P4 = 0 «Наше» уравнение: –1·x + 0·y –1·z + 4 = 0 Находим: P1 = – 1; P2 = 0; P3 = – 1.

2.Решаем уравнение для плоскости PD, параллельной плоскости PABC и проходящей через точку D. В общем виде такое уравнение имеет вид: P1·(x – xD) + P2·(y – yD) + P3·(z – zD) = 0. Используя параметры п.1, решаем (символьными вычислениями, жирный знак равенства <Ctrl>+<=>, символьный знак равенства «стрелка» <Ctrl>+<Shift>+<точка>, в слот solve, z). Получится так:

−1(x − x D) − 0 (y − y D) − 1 (z − z D) 0 solve ,z → −x + 11

(т. е. уравнение плоскости PD имеет вид z = – x + 11).

3. Для вывода чертежа плоскости и точки D на ней используем те же действия, что описаны в п. 2, 4, 5 этапа 1. Цвет точки D желательно выбрать тем же, что и для точки A (чтобы помнить, что в параллелограмме точки A и D соединяются ребром). Получим рис.2.57:

		x
PlaneD(x,y) :=		y		PD := CreateMesh (PlaneD,0,8,0,8,5,5)
	−x +		11

Обозначения точек внесены в среде MSPaint (в Mathcad внесение обозначений не предусмотрено). Эти обозначения нужны для пояснения этапов решения. Вы тоже можете их вставить. Для этого нужно выделить чертеж синим контуром, скопировать его в буфер (<Ctrl>+<C> или иконка копирования), вызвать MSPaint, извлечь в него рисунок из буфера (<Ctrl>+<V> или иконка вставки) и «подрисовать» обозначения.

Затем выделить нужную часть рисунка, скопировать в буфер, возвратиться в Mathcad, извлечь из буфера на поле второй страницы справа от «живого» чертежа. Вам легче будет следить за построениями.

Рис. 2.57.

Этап 2 завершен.

75

Указания к выполнению этапа 3 «Построение ребер параллело-

грамма AB, AC на плоскости PABC и ребра AD между плоскостями PABC

и PD». Для этой цели нужно использовать уравнение отрезка, соединяющего точки с заданными координатами. Имеется известное соотношение, связывающее текущие координаты (x, y, z) прямой с координатами (x0,

	y0, z0) и (x1, y1, z1) концов отрезка:	x −x0		=	y − y0		=	z −z0			. Но для
		x	−x		y	− y		z	−z	0
		1	0		1	0		1

построения ребер это уравнение использовать нецелесообразно по следующим причинам:

Во-первых, может оказаться, что у отрезка одна из координат одинакова, тогда знаменатель обратится в нуль, возникнет останов алгоритма из-за попытки деления на нуль. Придется вводить в общие формулы поправки (заменить формулу вводом одинаковой координаты), и формулы потеряют универсальность.

Во-вторых, возникнут трудности масштабирования, оно тоже окажется не универсальным.

Поэтому ниже использовано другое представление прямой – в параметрической форме: Прямая линия – одномерная, поэтому параметр u – единственный. Каждая из координат прямой линии рассчитывается так:

x0 Line(u) y 0

z 0

+(x1 − x0) u

+(y 1 − y 0) u

+(z 1 − z 0) u

Формула не содержит делений, поэтому более универсальна, чем приведенная выше. Если нужно показать только отрезок между x0 и x1, то параметр u изменяется в универсальном диапазоне, от 0 до 1, и это снимает трудности масштабирования. При u = 0 получаем точку (x0, y0, z0), при u = 1 получаем точку (x1, y1, z1), при изменении параметра u в пределах 0 < u < 1 получаем все промежуточные точки отрезка. Параметрическая форма идеально отвечает задаче построения ребер параллелограмма (т.е. отрезков прямых между вершинами).

Замечание: поскольку строится трехмерное изображение отрезков, нужно записывать в формулах не один, а два параметра (иначе Mathcad «не поймет», что требуется трехмерный график). Второй параметр задается произвольно и в расчетах не участвует.

76

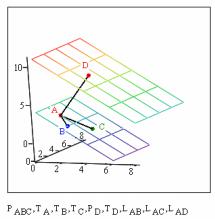
Используем параметрические уравнения прямых для построения ребер:

xA + (xB

− xA) u

Ребро АВ

(yB

Line

(u,v) := yA +

− yA) u

LAB := CreateMesh (LineAB,0,1,0,0)

AB

zA +

(zB − zA) u

Обратите внимание: масштаб

для CreateMesh получился

xA + (xC

− xA) u

универсальным: от 0 до 1 для

всех отрезков одинаково.

Ребро АС

(y

Line

(u,v) := y

A

+

C

− y

A

) u

LAC := CreateMesh (LineAC,0,1,0,0)

AC

zA +

(zC − zA) u

xA +

(xD

− xA) u

Ребро АD

(y

Line

(u ,v) := y

A

+

D

− y

A

) u

LAD := CreateMesh (LineAD,0,1,0,0)

AD

zA +

(zD − zA) u

u := 0.. 1

v := 0.. 1

(диапазон изменения параметров; диапазон для v

задается любым, v в вычисления не входит)

Обратите внимание: не нужно (но, конечно, можно) задавать шаг изменения параметра, достаточно указать 0 и 1 (отрезки прямой Mathcad построит самостоятельно).

Получим чертеж (рис. 2.58):

Рис. 2.58

Этап 3 завершен.

77

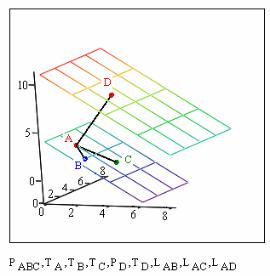
Указания к выполнению этапа 4 «Определение координаты чет-

вертой вершины параллелограмма (вершины E) на плоскости PABC. Построение граней CE, BE на этой плоскости». Нужно из точки B провес-

ти отрезок, параллельный отрезку AC и равный ему по длине. Используем коэффициент при параметре u такой же, как у ребра AC, но отсчет отрезка начинаем с координат точки B. Получим:

(xC − xA) u		Уравнение ребра, параллельного ребру АС
		и проходящего через точку В:
LineBE(u ,v) := PointB(u,v) +	(yC − yA) u
(zC − zA) u		LBE:= CreateMesh (LineBE,0,1,0,0)
Координаты точки E найдем, присваивая параметру u значение 1:
PointE(u ,v) := LineBE(1,0)		TE := CreateMesh (PointE,1,1,0,0)

После нахождения вершины E определяем уравнение ребра CE, используя формулы, описанные в Указаниях к этапу 3:

PointE(u,v)0 + (xC − PointE(u,v)0) u
LineCE(u,v) := PointE(u,v)1	+ (yC − PointE(u,v)1) u
		LCE:= CreateMesh (LineCE,0,1,0,0)
PointE(u,v)2	+ (zC − PointE(u,v)2) u

Получится так (рис. 2.59):

Рис. 2.59

Этап 4 завершен.

78

Указания к выполнению этапа 5 «Нахождение координат вершин F, G, H на плоскости PD, построение ребер BF, CG, EH между плоско-

стями PABC и PD». Техника расчета – та же, что использована в пояснениях к этапу 4 для построения ребра BE. Все ребра BF, CG, EH параллельны друг другу и параллельны уже построенному ребру AD. Поэтому используем тот же коэффициент при параметре u, что и для ребра AD, а отсчет отрезков (ребер) начинаем с точек B, C, E соответственно. Получим уравнения ребер и координаты вершин на плоскости PD (для этого в уравнениях ребер параметр u принимаем равным 1):

Получится так (рис.2.60):

79

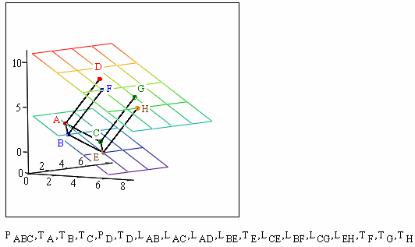
Рис. 2.60

Этап 5 завершен.

Указания к выполнению этапа 6 «Построение ребер FD, FH, HG,

DG на плоскости PD». Уравнения для ребер получаются как уравнения отрезков между заданными точками (см. Указания к выполнению этапа 3). Координаты вершин определены на этапе 5. Получим:

	PointF(u,v)0 + (xD − PointF(u,v)0) u
LineFD(u,v) := PointF(u,v)1			+ (yD − PointF(u,v)1) u
	PointF(u,v)2		+ (zD − PointF(u,v)2) u
	Point (u,v)0		+ (Point (u,v)0	− x ) u
		D	G	D
Line (u,v) :=	Point (u,v)1		+ (Point (u,v)1	− y	) u
DG		D	G		D
	Point (u,v)2		+ (Point (u,v)2	− z	) u
		D	G	D

PointF(u,v)0 + (PointH(u,v)0 − PointF(u,v)0) u

LineHF(u,v) := PointF(u,v)1 + (PointH(u,v)1 − PointF(u,v)1) uPointF(u,v)2 + (PointH(u,v)2 − PointF(u,v)2) u

Ребро FD

LFD := CreateMesh(LineFD,0,1,0,0)

Ребро DG

LDG:= CreateMesh(LineDG,0,1,0,0)

Ребро HF

LHF := CreateMesh(LineHF,0,1,0,0)

PointG(u,v)0

+

(PointH(u,v)0

− PointG(u,v)0) u

(PointH(u,v)1

LineGH(u,v) := PointG(u

,v)1

+

−

PointG(u,v)1) u

Ребро GH

,

v)2

+

(PointH(u

,

v)2

−

PointG(u

,

L

:= CreateMesh Line ,0,1,0,0

PointG(u

v)2)

u

GH

(

GH

)

Построение параллелограмма завершено (рис. 2.61):

80

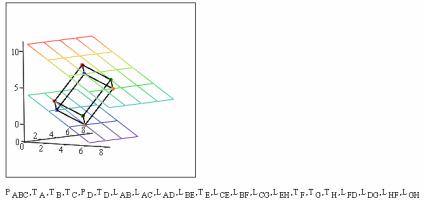
Рис. 2.61

Этап 6 завершен.

Указания к выполнению этапа 7 «Придание чертежу профессио-

нального вида: расчет масштабов для плоскостей PABC и PD, соответствующих координатам вершин параллелограмма, показ невидимых ребер пунктиром».

1. Сначала рассчитаем диапазоны переменных для плоскостей PABC и PD соответственно размерам параллелограмма. Для этого составим для каждой плоскости матрицу координат вершин так, чтобы координаты каждого аргумента (x, y, z) всех вершин находились в отдельном столбце. Затем найдем максимальные и минимальные значения координат x и y с помощью функции min( ), применяя ее к соответствующему столбцу. Составная матрица для вершин, расположенных на плоскости PABC, имеет вид:

Point ABCE:= stack stack stack Point A(1,0)T ,Point B(1,0)T ,Point C(1,0)T ,Point E(1,0)T

2. Без привычки такие сложные конструкты безошибочно создать трудно. Поэтому на первых порах лучше наращивать число строк матрицы постепенно, начиная с координат двух вершин. Последовательность действий:

•Выбираем произвольно две любые вершины (например, вершины A

и B). Их координаты заданы векторами PointA(1,0), PointB(1,0). Транспонируем векторы (<Ctrl>+<1>) и соединяем две строки «одна под другой», с помощью функции stack( ). Получится:

stack Point A(1,0)T ,Point B(1,0)T

•Охватываем полученный фрагмент синим контуром и вырезаем его в буфер (<Ctrl>+<x> или иконка «ножницы»)

81

•Для того чтобы подсоединить третью строку, соответствующую координатам вершины C, набираем stack( ). В слот, не думая, извлекаем из буфера часть формулы, заготовленной ранее (получится

stack	stack	Point		(1,0)T ,Point (1,0)T ). Перебрасываем синий
			A	B

контур направо (клавишей <Insert>), ставим запятую (получится

stack	stack	Point	A	(1,0)T ,Point (1,0)T		,				и в образовавшийся
				B

слот вводим Point C(1,0). Перебрасываем синий контур направо и нажимаем <Ctrl>+<1> для транспонирования. Получится:

stack stack Point A(1,0)T ,Point B(1,0)T ,Point C(1,0)T

• Точно так же добавляем координаты еще одной точки. Получится: stack stack stack Point A(1,0)T ,Point B(1,0)T ,Point C(1,0)T ,Point E(1,0)T

• Всю формулу вырезаем в буфер, набираем идентификатор Point ABCE:= и в слот извлекаем сконструированную формулу из

буфера. Получится нужный конструкт. Результат расчета (с пояснениями):

	Координаты:
		x		y		z
		1		2		3		Точка А
		2		1		2		Точка B
Point ABCE =
		3		3		1		Точка C
		4		2		0		Точка E

•Находим диапазон изменения аргументов x и y путем расчета минимального и максимального значения первого и второго столбцов (согласно нумерации, принятой в Mathcad – нулевого и первого столбцов). Извлечение столбца – клавишами <Ctrl>+<^>:

	0		0
xminABCE := min Point ABCE		xmaxABCE := max Point ABCE
xminABCE = 1		xmaxABCE = 4
	1		1
yminABCE := min Point ABCE		ymaxABCE := max Point ABCE
yminABCE = 1		ymaxABCE = 3

82

Правильность расчетов подтверждается просмотром столбцов мат-

рицы PointABCE.

Эти расчеты позволяют уточнить диапазон переменных для вывода плоскости PABC на чертеж:

P ABC := CreateMesh (Plane ABC,xminABCE,xmaxABCE,ymin ABCE,ymaxABCE,5,5)

Полностью аналогично определяем диапазон переменных для вывода плоскости PD.

Выводим чертеж и показываем невидимые ребра пунктиром (щелчком по графику вызываем окно форматирования графика, выбираем вкладку Special и для невидимых ребер указываем Line Style (стиль линий) Dashed (пунктир). Этой операцией заканчивается построение чертежа. Получится так (рис. 2.62):

83

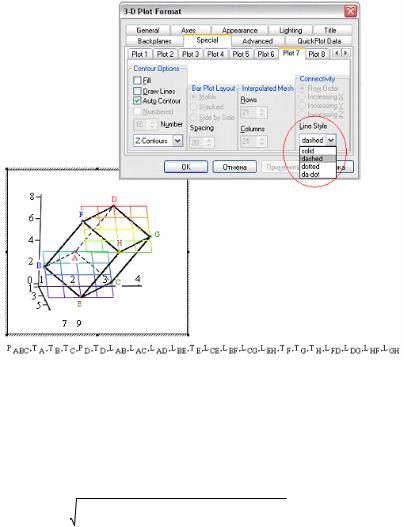
Рис. 2.62

Этап 7 завершен. Задания 1,2 выполнены.

8.2.2. Пояснения к заданию 3 «Найти длину ребер AB, GH».

Из курса алгебры мы знаем, что длина вектора определяется как корень квадратный из суммы квадратов разностей координат начала и конца вектора:

LengthAB := (xB − xA)2 + (yB − yA)2 + (zB − zA)2 LengthAB = 1.732

Средства Mathcad позволяют такие вычисления делать быстрее, с помощью встроенной функции «длина вектора», которая обозначается вертикальными линиями. Формируем разность векторов координат точек A и B и вычисляем длину:

LengthAB :=

PointB(1,0) − PointA(1,0)

LengthAB = 1.732

Длина ребра GH находится аналогично.

84

8.2.3. Пояснения к заданию 4 «Найти угол между ребрами AB и AC, сделать проверку».

Последовательность решения:

•Этап 1. Формируем векторы AB и AC, используя найденные выше координаты вершин A, B, C.

•Этап 2. Пользуясь встроенной процедурой Mathcad или формулой, изученной в курсе алгебры, находим скалярное произведение векторов AB и AC по значениям проекций этих векторов на оси.

•Этап 3. Сопоставляем результат этапа 2 с иной формулой скалярного произведения (произведение длин векторов на косинус угла между ними). Приравнивая два варианта формул скалярного произведения друг к другу, находим угол между векторами.

•Этап 4. Для проверки находим угол между векторами BA и BE, см. чертеж к этапу 7 заданий 1, 2. Для параллелограмма сумма углов междувекторами(AB, AC) и(BA, BE) должнасоставитьπ радиан(180°).

Выполнение этапа 1 «Формирование векторов AB и AC». Исполь-

зуя формулы алгебры, рассчитываем проекции векторов на оси по разности координат точек на их границах:

					1
AB := Point	(1,0)	− Point	A	(1,0)	AB =	−1
	B
						−1
					2
AC := Point	(1,0)	− Point	A	(1,0)	AC =	1
	C
						−2

Этап 1 завершен.

Выполнение этапа 2 «Расчет скалярного произведения векторов

AB и AC». Формула для расчета скалярного произведения ScalarAB_AC, известная из курса алгебры:

2
ScalarAB_AC := ∑ ABk ACk	ScalarAB_AC = 3

k= 0

ВMathcad имеется встроенная функция, позволяющая найти скалярное произведение быстрее, используя транспонирование одного из векто-

ров (любого) (<Ctrl>+<2>):

85

Обозначение транспонирования Т НЕ НАБИРАЙТЕ, используйте <Ctrl>+<1>

ScalarAB_AC := ABT AC

ScalarAB_AC = ( 3)

Этап 2 завершен.

Выполнение этапа 3 «Расчет угла между векторами». Используем способ вычисления скалярного произведения как произведения длин векторов на косинус угла между ними. Поскольку значение скалярного произведения вычислено (этап 2), то единственным неизвестным будет косинус угла между векторами. Найдем его (символьная процедура, вызывается <Ctrl>+<Shift>+<точка>). Длину вектора определяем так, как описано в Пояснении к заданию 3 (идентификатор вектора окружаем вертикальными линиями):

		В слот нужно вставить команду:
	Жирный знак равенства –
		solve, φ («Реши относительно φ»)
	<Ctrl>+<=>

AB AC cos (φ) Scalar AB_AC →

Вид формулы после вызова символьной процедуры <Ctrl>+<Shift>+<точка>)

В результате решения получим:

AB

AC

cos (φ)

Scalar

AB_AC

solve ,φ → acos 1

3

3

Так в Mathcad обозначается arccos()

Решение читается так: φ = arccos 3 . Если мы хотим увидеть чи-

3

словой ответ, нужно охватить формулу синим контуром и нажать знак равенства. Результат выведется в радианах:

AB

AC

cos (φ)

Scalar

AB_AC

solve ,φ → acos

1

3 = 0.955

3

Для того чтобы вывести ответ в градусах, нужно в слот ввести наименование единицы измерения: меню Insert (Вставить) Units (Единицы измерения) Angular (Единицы измерения углов) Degrees (Градусы)

86

Получим (рис. 2.63):

Рис. 2.63

AB

AC

cos (φ)

Scalar

AB_AC

solve ,φ → acos 1

3 = 54.736deg

3

Решение читается так: ϕ = 54.736°. Этап 3 завершен.

Выполнение этапа 4 «Проверка». Аналогично описанному вычисляем угол между векторами BA и BE. Получаем:

BA := PointA(1,0) − PointB(1,0)

BE:= PointE(1,0) − PointB(1,0)

T

BE

BA

BE

cos (ζ) solve ,ζ → π − acos

1

3

BA

3

Мы видим, что ϕ + ξ = π, как и должно быть в параллелограмме. Проверка успешно завершена.

Этап 3 завершен.

Выполнение задания 4 закончено. 87