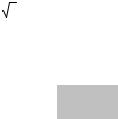
Охватите всё выражение вместе с обозначением интеграла синим контуром, затем введите символьный знак равенства (<Ctrl>+<Shift>+ <точка>) и щелкните левой кнопкой мыши где-нибудь вне формулы. Получится «живой» ответ:

	⌠	∞					1
			− x2
		e 2			1	2π2
				dx →
					2
	⌡					.
	0

Возможности символьных вычислений не исчерпываются описанными. Вы можете просмотреть и другие позиции меню Symbolics.

§15. Учебная задача

15.1. Постановка задачи

Mathcad, в отличие от текстового редактора Word или графического редактора Paint, требует не только (и не столько!) умения находить нужные опции и нажимать нужные клавиши. Необходимо наличие алгоритмического мышления, позволяющего составить и реализовать схему решения.

Чтобы проиллюстрировать это, решим довольно сложную задачу. Не поленитесь проделать весь путь от постановки задачи до полного ее решения. Это будет маленькой иллюстрацией к объему и сложности исследований, которые Вам придется часто делать при изучении естественнонаучных и профессиональных дисциплин.

ДАНО: радиус окружности r, координаты ее центра c1 (абсцисса) и c2 (ордината), параметры a и b уравнения прямой линии.

ПОЛУЧИТЬ: координаты пересечения окружности с прямой в функции от параметров задачи (a, b, r, c1, c2) и указать, при каких соотношениях этих параметров задача имеет решение.

15.2.Этапы решения (не только этой задачи, но и любой другой): 1. Обдумывание задачи.

2. Составление словесного описания алгоритма.

3. Формализация задачи.

4. Решение.

5. Графическое построение и проверка.

15.3.Выполнениеэтапа1 «Обдумываниезадачи» (безкомпьютера)

Работа над задачей начинается с ее обдумывания. По шутливому за-

кону «[Время на обдумывание задачи до выхода на компьютер] + [Время работы за компьютером] = const» затраты времени на обдумывание всегда

133

рентабельны. Мы понимаем, что задача не всегда имеет решение: может оказаться, что окружность и прямая вовсе не пересекаются. На рис. 4.1 показаны два случая: а) – решение существует, б) – решение не существует.

Рис. 4.1. Графическая иллюстрация к постановке задачи: (а) решение задачи существует; (б) решения отсутствуют.

Кроме того, ясно, что если решение существует, то могут быть либо 2 точки пересечения, либо одна (если прямая касается окружности).

Выполнение этапа 1 завершено.

15.4. Выполнение этапа 2 «Составление словесного описания алгоритма» (без компьютера).

Словесное описание алгоритма:

1.Составить уравнение окружности с параметрами (радиус окружности r, координаты ее центра c1 (абсцисса) и c2 (ордината)).

2.Составить уравнение прямой линии с параметрами a и b.

3.Составить систему уравнений для точек пересечения (эти точки должны удовлетворять как уравнению окружности, так и уравнению прямой, см. рис. 4.1-а).

4.Решить эту систему уравнений в символьной форме, получить ответ в виде координат двух точек пересечения.

5.Проанализировать решение. По смыслу задачи (рис. 4.1-б) в решение должны войти элементы, показывающие, что решение может не существовать. Зная уравнение окружности, догадываемся, что эти элементы будут входить в формулу под корнем, извлечение которого возможно только в том случае, если подкоренное выражение неотрицательно.

6.Находим соотношение между параметрами задачи (a, b, r, c1, c2), при которых подкоренное выражение будет положительным. При выполнении этого соотношения задача будет иметь 2 различных решения (прямая линия пересечет окружность в двух точках).

134

7.Находим соотношение между параметрами задачи (a, b, r, c1, c2), при которых подкоренное выражение будет равно 0. При выполнении этого соотношения задача будет иметь одно решение (прямая линия коснется окружности в одной точке).

8.Находим соотношение между параметрами задачи (a, b, r, c1, c2), при которых подкоренное выражение будет отрицательным. При выполнении этого соотношения задача не будет иметь решений (прямая линия не пересекает окружность).

Выполнение этапа 2 завершено.

15.5. Выполнениеэтапа3 «Формализация задачи» (накомпьютере)

Порядок действий следует пунктам 1, 2, 3 алгоритма, разработанного на этапе 2.

15.5.1. Выполнение пунктов 1, 2 алгоритма: составление уравне-

ний окружности и прямой линии. Из курса математики известно уравнение прямой Y = a X + b (параметр a характеризует наклон прямой по отношению к абсциссе X, а параметр b показывает, на какой отметке прямая линия пересекает ординату Y при X = 0). Также из курса математики известно уравнение окружности (X–c1)2 + (Y–c2)2 = r2 (параметры c1 и c2 – координаты центра окружности, параметр r – ее радиус).

15.5.2. Выполнение пункта 3 алгоритма: составление системы уравнений для точек пересечения (эти точки должны удовлетворять как уравнению окружности, так и уравнению прямой, см. рис. 4.1-а).

Составляем вектор, компонентами которого будут эти выражения (аналогично примеру 2 п. 14.4.1). Помним, что уравнения нужно записать с использованием жирного знака равенства <Ctrl>+<=>.

Образуйте «заготовку» для ввода вектора уравнений (можно через Меню Insert – Matrix, лучше (быстрее) с помощью клавиш <Ctrl>+<M>), укажите число строк (rows) 2, число столбцов (columns) 1. В появившуюся «заготовку» для вектора введите строки системы уравнений, используя жирный знак равенства (<Ctrl>+<=> ). Должно получиться:

	(Y − a X − b)						0
	(X − c 1)	2	+ (Y − c 2)		2		2
							− r		0		(4.1)

Набор c1 и c2 – через так называемую КОСМЕТИЧЕСКУЮ точку. Здесь цифры 1 и 2 – не индексы, а просто запись идентификатора в форме, принятой в научной литературе: вместо c1 записываем c1 для красоты. Набираем так: с (точка) 1, при этом каретка смещается на 0.5 межстрочного интервала. НЕ НУЖНО ПУТАТЬ с индексом, который набирается с помощью квадратной скобки [.

Напоминание: для набора показателя степени используйте клавиши <Shift>+<6> (клавиша 6 – в верхнем ряду, где ^).

Выполнение этапа 3 завершено.

135

15.6. Выполнение этапа 4 «Решение» (на компьютере)

15.6.1. Выполнение пункта 4 алгоритма: решение системы урав-

нений, определяющих координаты точек пересечения, получение от-

вета в символьном виде (в виде формул для расчета координат двух точек пересеченияпозаданнымпараметрампрямой(a, b) иокружности(c1, c2, r)).

После этого делайте так, как в примере 2 п. 14.4.1 описания символьных вычислений. Кратко:

Охватите синим контуром ф-лу (4.1);

Введите символьный знак равенства клавишами <Ctrl>+ <Shift>+<точка>;

В слот введите через запятые запрос на решение и перечень искомых переменных solve,X,Y и щелкните левой кнопкой мыши гденибудь вне формулы.

Ответ, который Вы увидите, будет огромным. Мы видим, что он

представлен в форме матрицы размера 2×2.

136

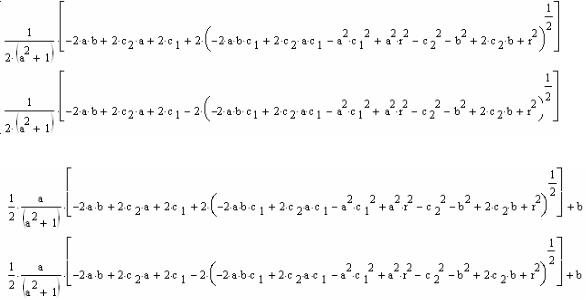
137

Первый столбец ответа выглядит так:

(4.2 а)

второй столбец ответа выглядит так:

(4.2 б)

«Расшифруем» ответ Mathcad. Верхняя строка даст абсциссу (элемент матрицы с индексами 0,0) и ординату (элемент матрицы с индексами 0,1) первой точки пересечения, а вторая – то же для второй точки (элементы матрицы с индексами 1,0 и 1,1):

Элемент0,0 Элемент0,1 Элемент1,0 Элемент1,1 .

Нужно привыкнуть, что нумерация элементов массива в Mathcad сле-

дует американскому стилю (не с 1, а с нуля!).

Просмотрите полученный ответ. А теперь представьте, сколько ошибок в выкладках Вы сделали бы, если бы выводили такое выражение вручную!

15.6.2. Выполнение пункта 5 алгоритма: анализ решения.

1) Подготовительные операции. Скопируйте ответ (только ответ!)

целиком: охватите его синим контуром, затем используйте иконку «копия» или лучше (быстрее) нажмите <Ctrl>+<C>. Копия будет передана в буфер для хранения и для последующего использования.

Присвойте скопированной матрице какой-либо идентификатор (например, Z – прописная литера), нажмите <двоеточие> и в появившийся слот введите копию из буфера (либо иконкой «извлечь из буфера», либо нажмите <Ctrl>+<V>). Получится (формула приведена не полностью, изза своего большого размера):

		1		−2 a b + 2 c a + 2 c				+ 2		−2 a b c		+ 2 c a c		− a2 c	2	+ …
		2 (a2 + 1)
Z :=						2	1				1	2	1		1
		1												2	2
					−2 a b + 2 c	a + 2 c		− 2		−2 a b c		+ 2 c a c		− a c		+ …
		2 (a2 + 1)
						2	1				1	2	1		1	(4.3)

Итак, мы заготовили матрицу, в которой записан ответ задачи: координаты точек пересечения окружности и прямой линии.

2) Нахождение фрагментов формул, по которым можно устано-

вить, имеется ли решение. Как указывалось в описании алгоритма, по смыслу задачи (рис. 4.1-б) в решение должны войти элементы, показывающие, что решение может не существовать. Мы видим, что в каждом из элементов матрицы Z имеется одинаковое выражение в форме квадратного корня:

											1
	−2 a b c	1	+ 2 c a c	1	− a2 c	2	+ a2 r2 − c	2	− b2 + 2 c b + r2	2		(4.4)
			2			1		2	2

138

Из курса элементарной математики Вы знаете, что извлечение корня возможно только в том случае, когда подкоренное выражение неотрицательно. Следовательно, для того чтобы гарантировать наличие решения, нужно, чтобы соотношение параметров задачи (a, b, c1, c2, r) было таким, чтобы подкоренное выражение было неотрицательным.

15.6.3. Выполнение п. 6, 7, 8 алгоритма: нахождение соотношения между параметрами задачи (a, b, r, c1, c2), при которых подкоренное выражение будет:

Положительным. При выполнении этого соотношения задача будет иметь 2 различных решения (прямая линия пересечет окружность в двух точках).

Нулевым. При выполнении этого соотношения задача будет иметь 2 различных решения (будут получены 2 варианта прямых линий, каждая из которых будет касаться окружности в одной точке на противоположных концах диаметра окружности).

Отрицательным. При выполнении этого соотношения задача не будет иметь решения (прямая линия не пересечет окружность).

1) Предварительные замечания. Мы видим, что граница между об-

ластью параметров, в которой отсутствует решение, и областью, в которой прямая линия пересекает окружность в двух точках, проходит через соотношение, в котором подкоренное выражение равно 0.

	−2 a b c		+ 2 c	a c		− a2 c	2	+ a2 r2 − c	2	− b2 + 2 c	b + r2			0 (4.5)
		1			1		1		2
				2							2

Таким образом, решение вопроса о существовании точек пересечения прямой линии и окружности свелось к простой задаче: выразить один из параметров (любой) через все другие так, чтобы подкоренное выражение получилось равным нулю.

2) Формула, связывающая один из параметров (a, b, r, c1, c2) задачи через остальные параметры, при которых подкоренное выражение рав-

но 0. Выберем один из параметров (например, b) и выразим его через остальные (a, r, c1, c2), с использованием символьного решения уравнения

подкоренное выражение = 0.

Действуем так, как в примере 1 п. 14.4.1 описания символьных вычислений. Кратко:

Наберите формулу (4.5) ОБЯЗАТЕЛЬНО через жирный знак ра-

венства (<Ctrl>+<=>).

Введите символьный знак равенства клавишами <Ctrl> + <Shift>

+<точка>;

В слот введите через запятые запрос на решение и перечень искомых переменных solve,b и щелкните левой кнопкой мыши где-нибудь вне формулы).

139

Должно получиться так:

(4.6)

3) Ответы.

а) Условия, при которых прямая линия касается окружности. Из геометрических соображений ясно, что таких прямых линий будет две: одна коснется окружности «сверху», а другая – «снизу», на противоположном конце диаметра, проходящего через первую точку касания.

Введите идентификатор функции b1(a, c1, c2, r) для обозначения функциональной зависимости параметра b от других параметров (a, c1, c2, r), нажмите двоеточие и в появившийся слот введите копию первого элемента вектора-решения (это будет условием касания прямой линии окружности «сверху»). Копию делайте так: охватите нужную часть формулы синим контуром, нажмите <Ctrl>+<C> (т. е. скопируйте ее в буфер), затем установите курсор в слот и извлеките копию из буфера (лучше всего – клавишами <Ctrl>+<V>).

Получится:

	1
b1(a,c 1,c 2,r):= −a c 1 + c 2 + (a2 r2 + r2)2		(4.7)

Затем введите другой идентификатор функции b2(a, c1, c2, r) , нажмите и двоеточие и в появившийся слот введите копию второго элемента вектора-решения (это будет условием касания прямой линии окружности «снизу»).

Получится:

	1
b2(a,c 1,c 2,r):= −a c 1 + c 2 − (a2 r2 + r2)2			(4.8)
Функцииb1(a, c1, c2, r) иb2(a, c1, c2, r) отличаютсязнакомпередкорнем.
Таким образом, ответом на вопрос о касании окружности			прямой

линией будет:

ЕСЛИ [b = b1(a, c1, c2, r)] ИЛИ [b = b2(a, c1, c2, r)] ТО прямая касается

окружности	.	(4.9)

140

б) Условия, при которых прямая линия не пересекает окружность.

Параметр b в уравнении прямой линии показывает, на какой отметке прямая линия пересекает ординату, когда абсцисса равна нулю, см. п. 15.5. Значения b1(a, c1, c2, r) и b2(a, c1, c2, r) определяют граничные значения этой отметки: если прямая линия пересекает ординату выше отметки b1(a, c1, c2, r) или ниже отметки b2(a, c1, c2, r), то она проходит выше или ниже окружности, не пересекая ее.

Таким образом, ответом на вопрос об отсутствии пересечения окружности и прямой будет:

ЕСЛИ [b > b1(a, c1, c2, r)] ИЛИ [b < b2(a, c1, c2, r)] ТО пересечение от-

сутствует	.	(4.10)
в) Условия, при которых прямая линия пересекает		окружность в

двух точках. Если прямая линия пересекает ординату ниже отметки b1(a, c1, c2, r) и выше отметки b2(a, c1, c2, r), то она проходит через точки внутри и пересекает ее в двух точках.

Таким образом, ответом на вопрос об отсутствии пересечения окружности и прямой будет:

ЕСЛИ [b < b1(a, c1,c 2, r)] И [b > b2(a, c1,c 2, r)] ТО пересечение в двух

точках	.	(4.11)
Выполнение этапа 4 завершено.

15.7. Выполнение этапа 5 «Графическое построение и проверка»

(на компьютере)

15.7.1. Идея проверки правильности вычислений. Представим себе,

какой результат мы ожидали бы увидеть на графике, показывающем окружность и касающиеся ее прямые. ТАКОЕ ПРЕДЧУВСТВИЕ РЕЗУЛЬТАТА ВСЕГДА ПОЛЕЗНО! Если задаться значениями параметров (a, c1, c2, r), а затем вычислить b1(a, c1, c2, r), то прямая линия a x + b1(a, c1, c2, r) коснется окружности в одной из точек. Если при тех же параметрах (a, c1, c2, r) вычислить b2(a, c1, c2, r), то прямая линия a x + b2(a, c1, c2, r) коснется окружности в точке на противоположном конце диаметра, проходящего через первую точку. Обе эти касательные будут параллельными (т. к. у них одинаковый угол наклона, определяемый параметром a).

15.7.2. Реализация идеи.

1) Сначала проверим, правильно ли мы определили координаты точек касания. Мы уже выполнили необходимые расчеты: координаты находятся в массиве Z (формула (4.3)), осталось только обозначить ответ как функцию переменной b. Для этого просто подправьте (не набирайте снова!) формулу (4.3): запишите слева Z(b) вместо Z.

141

Получится (формула приведена не полностью, из-за своего большого размера):

c1 := 2

c2 := 4

r := 10

a := 0.5

		1			−2 a b + 2 c a + 2 c		+ 2	−2 a b c		+ 2 c a c		−
		2 (a2 + 1)
Z(b) :=					2	1			1	2	1
		1			−2 a b + 2 c a + 2 c		− 2	−2 a b c		+ 2 c a c		−
		2 (a2 + 1)
					2	1			1	2	1	…(4.12)

Мы выводили ф-лу (4.3) для определения координат двух точек пересечения окружности прямой линией. Пока прямая проходит через точки внутри окружности, таких точек действительно будет две, и они должны иметь различные координаты. Если прямую смещать так, как показано стрелкой на рис. 4.2, то точки пересечения будут сближаться, а затем сольются в одну (это и будет точкой касания), и их координаты будут

одинаковыми.

Проверим, получились ли одинаковые числа в строках матрицы (4.12). Наберите

	Z(b1(a,c 1,c 2,r)) = и Z(b2(a,c 1,c 2,r)) =.
	Если окажется, что первая и вторая строки у каж-
	дой матрицы одинаковые, то это убедит Вас в
	правильности нахождения точек касания.
Рис. 4.2. Сближение точек	2) Реализация проверки с помощью графика.
пересечения.	Построим график и укажем на нем не только ок-
	ружность и касательные к ней (если получатся

правильно), но и координаты точек касания.

Фаза 1 построения графика. Для построения графика нужно научиться строить окружность. Это можно сделать разными способами, самый простой из которых – использовать параметрическое представление окружности:

Задаться значениями угла поворота радиуса окружности вокруг центра в пределах от 0 до 2π:

ϕ := 0,0.01.. 2 π

(это и будет один из наших параметров; второй параметр – радиус окружности).

Абсцисса с учетом того, что координаты центра окружности равны

142

(с1, с2), вычисляется так:

r cos (ϕ) + c 1

(эту формулу не набирайте, покажем ее прямо на графике).

Ордината с учетом того, что координаты центра окружности равны (с1, с2), вычисляется так:

r sin(ϕ) + c 2

(эту формулу тоже не набирайте, покажем ее прямо на графике).

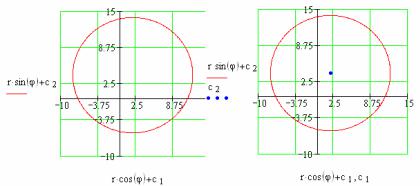
Теперь образуйте шаблон графика (можно из меню Insert – Graph – XY plot; лучше (быстрее) клавишами <Shift>+<2>) и в слоты абсциссы и ординаты впишите формулы, как показано на рис. 4.3-а.

а)

б)

Рис. 4.3. Начальный этап построения графика для проверки правильности расчетов: а) график окружности, б) отметка центра окружности.

Приведите график к надлежащему виду, введя нужные опции щелчком мыши по полю графика: нанесите сетку (опция XY-axes, включите Grid lines, отключите AutoGrid и введите число градаций сетки – например, 4 на каждой из осей); перейдите к «русской» форме указания координат (опция XY-axes, кнопка Crossed). Добейтесь, чтобы график выглядел так, как на рис. 4.3.

Укажите (точкой) центр графика. Для этого введите дополнительные координаты (как на рис. 4.3-б). Способ ввода: охватите уже имеющуюся подпись оси синим контуром и нажмите запятую. Появится новый слот, в который можно ввести новые координаты. Укажите, что вывод нужно сделать точкой. Для этого щелчком мыши вызовите опции графика, выберите вкладку Traces (линии графика), перейдите ко второй строке (trace 2), откройте список типов Types (типы линий) и выберите points (точки). В списке Width (ширина) выберите 3, в списке Color выберите

143

цвет, какой хотите. Нажмите OK. Должно получиться как на рис. 4.3-б.

Фаза 1 построения графика завершена.

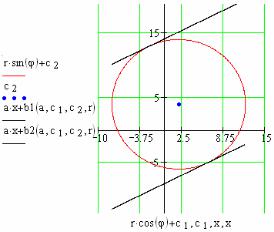
Фаза 2 построения графика. Представим графически прямые, которые (как мы предполагаем) должны касаться окружности в двух точках по разные стороны диаметра. Для этого введем диапазон и шаг изменения аргумента x:

x:= −r + c 1,−r + c 1 + 0.01..r + c 1

(4.13)

Напоминание: многоточие наберите с помощью клавиши <точка_с_запятой>.

Обратите внимание на то, что при определении диапазона возможных изменений аргумента нужно учитывать координаты центра окружности!

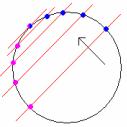
Затем образуем два дополнительных слота по осям абсцисс и ординат (охватите синим контуром «старый» аргумент, затем нажмите клавишу <запятая>). В эти слоты введем уравнения касательных, приведенных в п. 15.7.1. Должно получиться так, как показано на рис. 4.4.

Рис. 4.4. Проверка правильности нахождения уравнений касательных к окружности.

Замечание: график имеет функцию автоматического масштабирования, в результате окружность может принять форму эллипса. Растяните график так, чтобы устранить искажение.

Фаза 2 построения графика завершена.

Фаза 3 построения графика. Покажем на графике точки касания (для проверки, правильно ли мы их рассчитали). Все необходимые вычисления уже сделаны, см. формулу (4.12). Осталось в качестве аргумента b указать b1(a, c1, c 2, r) и b2(a, c1,c 2, r), а в слотах абсциссы и ординаты указать соответствующие элементы матрицы Z(b). Как уже упоминалось, нумерация элементов – с нулевого.

Образуйте еще два слота на осях графика и впишите в них координа-

144

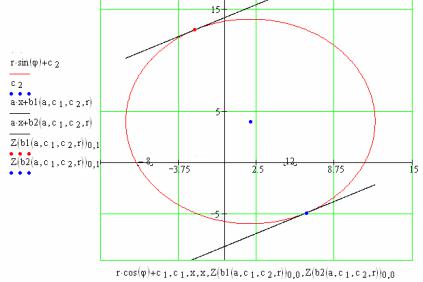
ты точек касания. Опции для этих координат: тип (Types) – точки (points), толщина (Weight) – не менее 3. Должно получиться так, как показано на рис. 4.5. Номера элементов набирайте так: после набора идентификатора матрицы, например, Z(b1(a, c1, c2, r)) охватите его синим контуром, нажмите клавишу <открывающая квадратная скобка – [> и в появившийся слот впишите номер элемента матрицы – как на рис. 4.5.

Фаза 3 построения графика завершена.

Построенный график показывает, что в вычислениях нет грубых ошибок, график соответствует нашим интуитивным представлениям о результате: прямые линии действительно касаются окружности, координаты точек касания находятся по разные стороны диаметра. Но проверка по графику, хотя и очень полезная, не обладает достаточной точностью и, главное, общностью (не защищена от случайных совпадений). Для чистоты ответа сделаем еще одну, более точную проверку.

Рис. 4.5. Проверка правильности нахождения координат точек касания.

3) Проверка правильности расчета вычислениями. Идея проверки состоит в ответах на два вопроса:

1.Действительно ли обе точки касания лежат на одной прямой?

2.Действительно ли эта прямая проходит через центр окружности? Важное замечание: непосредственно для решения задачи ответ на эти вопросы не нужен. Такие (казалось бы) лишние вычисления служат ловушкой для логических ошибок. Ловушки в форме про-

145

верки выполнения некоторых тождеств, равенств и т. п. полезно вставлять в программы. Академик А. П. Ершов, много сделавший для развития науки программирования, назвал такие ловушки УТВЕРЖДЕНИЯМИ и настаивал на их огромном значении для обнаружения и исправления логических ошибок – наиболее трудно обнаруживаемых ошибок в алгоритмах, не проявляющих себя в переполнениях, делении на нуль и прочих действиях, обнаруживаемых компьютером без участия программиста. К сожалению, иногда при наличии логической ошибки результат расчета получается внешне правдоподобным, и программист может посчитать свою задачу выполненной. Но при использовании других исходных данных ответ будет абсолютно неверным! Если программа используется для принятия решения или для управления производством, результат логической ошибки может оказаться катастрофическим (ошибка такого рода привела к гибели космического корабля и к Чернобыльской трагедии).

Перейдем к реализации идеи проверки-ловушки по следующей схеме:

1.Составим уравнение прямой линии, проходящей через две точки: через центр окружности и через одну из точек касания.

2.Подставим в это уравнение координаты второй точки касания.

3.Если окажется, что координаты второй точки удовлетворяют уравнению – расчеты выполнены правильно, логическая ошибка, скорее всего, отсутствует.

Уравнение прямой Y(X), проходящей через две точки с координата-

ми [x1; y(x1)], [x2; y(x2)] имеет вид:

X − x	1				Y( X) − y(x )
					1
					y(x 2) − y(x1)
x2 − x1						(4.14)

Подставим в (4.14) в качестве первой точки [x1; y(x1)] координаты центра окружности [c1; c2], а в качестве второй точки [x2; y(x2)] – коорди-

наты одной из точек касания, например: [Z(b1(a, c1, c2, r))0,0 ; Z(b1(a, c1, c2, r))0,1]. В качестве точки с координатами [X;Y(X)], предположительно

лежащей на прямой (4.14), возьмем вторую точку касания с координата-

ми [Z(b2(a, c1, c2, r))0,0 ; Z(b2(a, c1, c2, r))0,1 ].

Ели логической ошибки в наших расчетах нет, то после подстановки разность между правой и левой частями (4.14) будет равна нулю.

Проверяем. После набора разности наберите знак равенства (обычный) и посмотрите, действительно ли в ответе получился нуль. Желаю удачи!

Z(b2(a ,c 1,c 2,r ))0,0 − c 1

−

Z(b2(a ,c 1,c 2,r ))0,1 − c 2

=

Z(b1(a ,c

1

,c

2

,r ))0,0

− c

1

Z(b1(a ,c

1

,c

2

,r ))0,1

− c

2

(4.15)

146

Напоминание: чтобы перейти к набору индексов, нужно нажать клавишу <квадратная открывающая скобка [>.

4. Иллюстрацию условий наличия (4.10) и отсутствия (4.11) пересе-

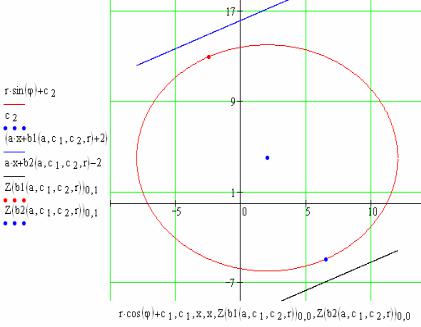
чения окружности и прямой легче всего провести, копируя рис. 4.5 и «подправляя» значение аргументов в уравнениях прямых линий.

а) Длятогочтобыпроиллюстрироватьотсутствиепересечения, введите: a x + b1(a, c1,c 2, r)+2 вместо a x + b1(a, c1,c 2, r);

a x + b2(a, c1,c 2, r) – 2 вместо a x + b2(a, c1,c 2, r).

Должно получиться так, как показано на рис. 4.6.

Рис. 4.6. Проверка правильности нахождения условий отсутствия пересечений.

б) Для того чтобы проиллюстрировать наличие пересечений, скопируйте рис. 4.6 и введите:

a x + b1(a, c1,c 2, r) – 2 вместо a x + b1(a, c1,c 2, r) + 2; a x + b2(a, c1,c 2, r) + 2 вместо a x + b2(a, c1,c 2, r) – 2.

Должно получиться так, как показано на рис. 4.7.

147