5.5. Векторно-матричное описание

При переходе к дискретной аппроксимации непрерывной части системы будем считать, что входной сигнал квантуется с периодом Т, а затем преобразуется экстраполятором нулевого порядка.

Это значит, что внешнее воздействия U(t) остается постоянным в течение n-такта квантования, т. е. U(t) = u(nT), при nT t (n + 1)T.

Известно, что решением основного векторно-матричного уравнения непрерывной системы =AX+BU является следующее выражение

X(t) = Ф(t)X(o) +, (5.1)

где Ф(t)= e^At - переходная матрица системы, имеющая форму матричной экспоненты e^At. Она вычисляется либо как сумма степенного ряда e^At = I + + At + +…+ +…, либо как обратные преобразования Лапласа e^At = = L^-1{(SI - A)^-1}.

Используем выражение (5.1) для определения вектора состояния во времени интервала nTt(n+1)T, считая начальными условиями x(nT), X(t) = = Ф( - nT)X(nT) + u(nT). Для момента времени t = (n + 1)T имеем X[(n + 1)T] = Ф(T)X(nT) + U(nT), или после преобразованийX(n + 1) = Ф(T)X(n) + … + U(n), гдеФ(T) = e^AT =L^-1{(SI-A)^-1} - - переходная матрица непрерывной части системы при t = T.

Введем обозначения: A* = Ф(T); B*=[]B. Тогда векторно-матричное описание дискретной системы будет иметь вид:

X(n + 1) = A*X(n) + B*U(n), Y(n) = CX(n) + DU(n).

По форме полученные уравнения являются полной аналогией векторно-матричных уравнений непрерывной системы.

Векторно-матричное описание дискретной системы

Пусть дискретная система описывается передаточной функцией

W(z) = = .

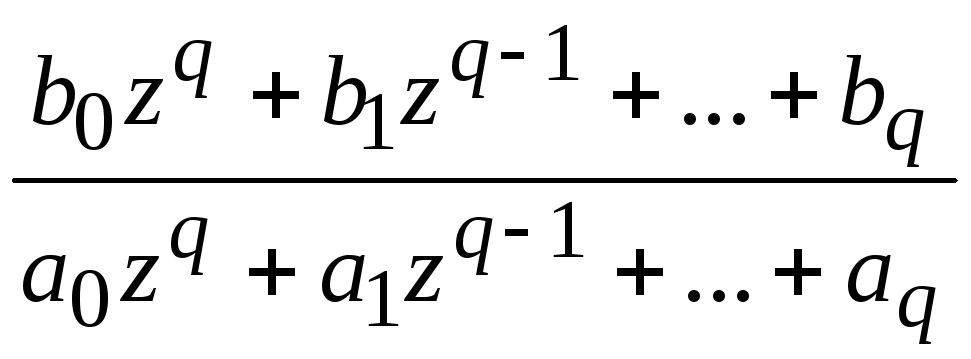1. Ей соответствует разностное уравнение

a₀y(n + q) + a₁y(n + q - 1) +…+ a_qy(n) = b₀u(n + q) + b₁u(n + q - 1) +…+ b_qu(n).

Переменные состояния примем следующие:

X₁(n) = y(n);

X₂(n) = x₁(n + 1) = y(n + 1);

X₃(n) = x₂(n + 1) = y(n + 2);

………………………………

X_q(n) = x_q-1(n + 1) = y(n + q - 1);

X_q(n + 1) = y(n + q).

Подставим их в разностное уравнение, приняв a₀ = 1, b_q = 1, b₀ = b₁ = = … = b_q-1 = 0, y(n+q) = x_q(n+1) = - a₁x_q(n) - a₂x_q-1(n) -…- a_qx₁(n) + u(n).

Полученные уравнения можно представить в виде векторно-матричного уравнения состояний:

= +

Совместно с уравнением выхода

Y(n)=[10…0].

Вводя обозначения: X – вектор переменных состояния; А - матрица системы; В – матрица входа; С –матрица выхода; - записываем векторно-матричное уравнение дискретной системы в комплексной форме:

X(n + 1) = AX(n) + BU(n); Y(n) = CX(n).

Можно получить выражения матриц A,B и С и в более общем случае, когда b_q 1 и b₀ b_q-10 [1].

Решение дискретного уравнения состояния с помощью

Z-преобразования

Рассмотрим дискретное уравнение состояния X(n+1)=A*X(n)+B*U(n), где A* = e^AT= L^-1{(SI-A)^-1}|_t=T; B* = []B. Подвергнем обе части уравнения состояния Z-преобразованию zX(z) - zX(0) = A*X(z) + B*U(z). Отсюда X(z) = (zI - A*)^-1zX(0) + (zI - A*)^-1B*u(z). Подвергая обратному Z- преобразованию, имеем X(n) = Z^-1{(zI - A*)^-1z}X(0) + Z^-1{(zI - A*)^-1B*u(z)}. Покажем, что обратное Z – преобразование от (zI - A*)^-1 есть дискретная переходная матрица состояния A(kT).

Z – преобразование A(kT) определяется общей формулой Z –преобразования A(z) = =. Умножим обе части последнего уравнения на A*z^-1 и вычтем результат из последнего уравнения. Получим (I - A*z^-1)A(z) = I, откуда A(z) = (I - A*z^-1)^-1 = (zI - A*)^-1z.

Вычисляя обратное Z – преобразование, получим A(kT) = Z^-1{(zI-A)^-1z}.

Это выражение и является основой способа определения переходной матрицы состояния, основанного на Z – преобразовании.

Второе слагаемое в выражении для X(n) вычисляем с помощью теоремы свертки и выражение для A(kT);

Z^-1{(zI - A*)^-1B*U(z)} =