лекции мат. анализ

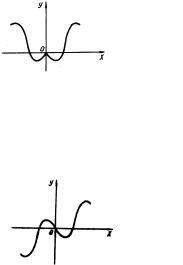
Функция ) называется четной, если для всех х из области определения. График четной функции симметричен относительно оси ординат (рис. 2.5.).

		Рис. 2.5.
		Примерами четных функций являются функции:	,
	,	.

Функция называется нечетной, если для всех из области определения. График нечетной функции симметричен относительно начала координат (рис. 2.6.).

			Рис. 2.6.
Нечетными, например, являются		функции		,
Для прочих функций эти особенности не имеют место. Напри-
мер, функции	или		не являются ни чет-

ными, ни нечетными (общего вида), их графики не симметричны ни относительно оси ординат, ни относительно начала координат.

2. Периодичность функции.
Функция	называется периодической,	если существует
такое постоянное число	, что	в области опре-

деления функции. При этом наименьшее из положительных чисел , удовлетворяющих данному свойству, называется периодом. Примером периодических функций служат тригонометрические функции

Период первых двух функций равен 2π, а две последние имеют период, равный π. График периодической функции достаточно построить на отрезке длины , далее эта кривая повторяется на всю область существования функции.

3. Монотонность функции.

Функция	называется возрастающей (убывающей) на
интервале	принадлежащем области существования этой функ-
	11

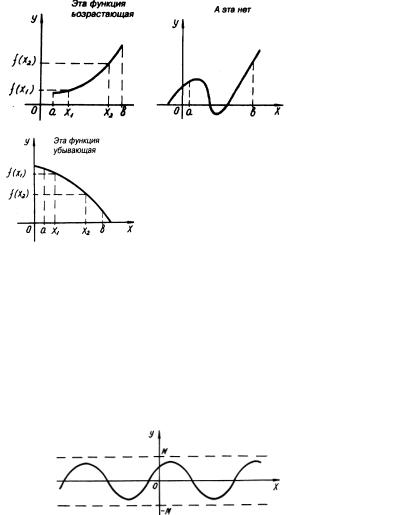
ции, если большему значению аргумента в этом интервале соответствует большее (меньшее) значение функции. Это значит, что для лю-

бых значений	имеем неравенство	(рис. 2.7.), а в
случае убывания	- неравенству	соответствует неравенство
(рис. 2.8.).

Рис. 2.7.

	Рис. 2.8.
Еcли функция	определенная на интервале, является

только возрастающей или только убывающей на этом интервале, то она называется монотонной на интервале.

4. Ограниченность функции.
Функция	заданная на интервале	называется

ограниченной на этом интервале, если существует, такое положитель-

ное число	, что для всех из данного интервала верно неравен-
ство	.
Например, тригонометрические функции
ограничены на всей области их существования, и число		для
них равно 1.График ограниченной функции лежит в полосе
( рис.2.9.).

Рис. 2.9.

12

1.7. Элементарные функции

Напомним определения и свойства некоторых элементарных функций, известные из школьного курса математики. В каждом случае укажем аналитическое выражение и область определения функции, приведем ее график.

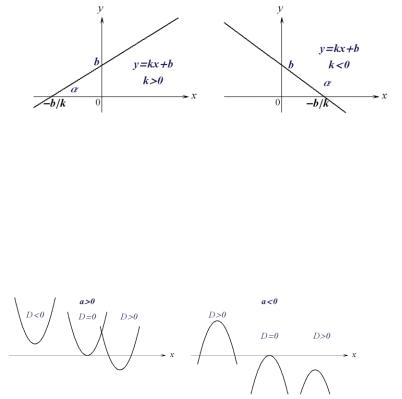
1) Линейная функция:

y kx b, x R,

где k и b – некоторые постоянные (числа); график – прямая с угловым коэффициентом k ( k tg , где – угол наклона прямой к

оси x ):

Рис.2.10.

2) Квадратичная функция:

y ax2 bx c

(a 0) x R,

где a , b , c - постоянные коэффициенты; график – парабола, ее расположение существенно зависит от величины

D b2 4ac ,

называемой дискриминантом функции, и от знака первого коэффициента a :

Рис.2.11.

3) Обратно пропорциональная зависимость:

13

	y	k	(k 0),	x 0 ,
		x

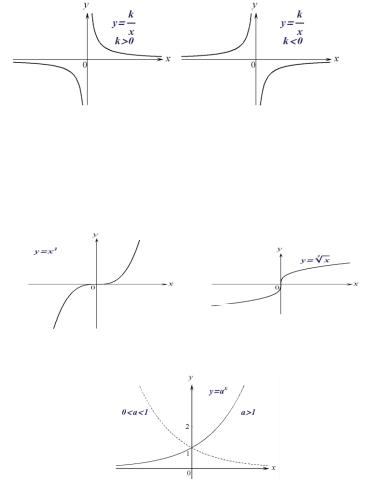
где k - постоянная. График – гипербола:

			Рис. 2.12.
4)	Степенная функция:
			y kxn	(k 0) ,
где и - постоянные; область определения существенно зави-
сит от	) рассмотрен случай			(обратная пропорциональность)и
случай			. Приведем еще графики функций для		и		:
5)	Показательная функция:

		Рис.2.13.
y a x
	(a 0, a 1), x R,

где a - постоянная; график в зависимости от значения a имеет

вид:

Рис. 2.14. 6) Логарифмическая функция:

14

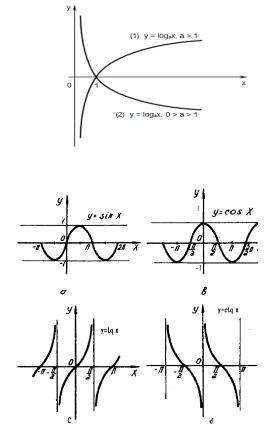
Рис. 2.15. 7) Тригонометрические функции.

Рис.2.16.

Все перечисленные здесь функции, а также и обратные тригонометрические функции являются основными элементарными функци-

ями.

1.8. Сложная функция

Пусть заданы функции y f (x) и z F( y) , причем множество значений функции f принадлежит области определения функции F : E( f ) D(F) . Тогда можно определить сложную функцию

z F( f (x)),

x D( f ) ,

называемую также композицией функций f и F .

15

Пример. Из функций y x2 x и y 2x с помощью указанной операции можно составить две сложные функции: y 2x2 x и y (2x )2 2x 4x 2x .

Используя операцию композиции, можно из основных элементарных функций, получать новые функции, также называемые элементарными. Вообще, элементарной функцией называют функцию, которую можно получить из основных элементарных функций с помощью конечного числа арифметических операций и композиций.

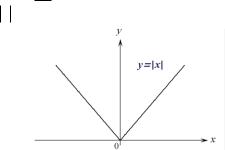
Пример. Функция			x	при	x 0,	(читается: ―модуль
	y	x
			x	при	x 0
x ‖) является элементарной, так как для всех					x R справедливо пред-

ставление x x2 . График этой функции приведен на рис. 2.17.

Рис. 2.17.

1.9. Обратная функция

Рассмотрим функцию y f (x) с областью определения X и множеством значений Y. Предположим, что для любого y Y уравнение f (x) y имеет единственное решение x X . Тогда на множестве Y можно определить функцию, сопоставляющую каждому y Y

такое значение x	X , что f (x) y .	Эту функцию называют обрат-
ной для функции f	и обозначают f 1 :	x f 1( y),	y Y .

Функцию, у которой существует обратная функция, называется

обратимой.

Из определения обратной функции вытекает, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

16

Обозначая, как обычно, аргумент функции через x , а значение

функции через y , можно записать:	y f 1(x),	x	Y .
Поскольку взаимная перестановка переменных		x	и y равно-

сильна переобозначению координатных осей, можно показать, что график функции y f 1(x) симметричен графику функции y f (x)

относительно биссектрисы первого и третьего координатных углов (то есть относительно прямой y x ).

Примеры. 1) Для линейной функции y 2x 6 обратная функция также линейна и имеет вид x (1/ 2) y 3 . Меняя местами x и y , получаем y (1/ 2)x 3 . Графики исходной и обратной функций приведены на рис. 2.18.

			Рис.2.18.						Рис.2.19.
2)			Для функции	y x2 , x			X [0, ) , множество
									значений
имеет вид Y [0, ) .				Для каждого y Y уравнение				имеет един-
ственное решение x
					y X . Поменяв местами x и			y , получим
			x [0, ) . Графики функций приведены на рис. 2.19 .
y x ,
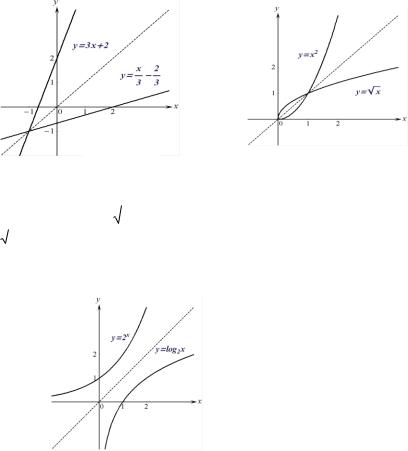
3)			Обратной к показательной функции y ax является лога-
рифмическая функция				y loga x, x 0 . На рис. 2.20.				представлены

Рис.2.20.

графики функций y 2x и y log2 x .

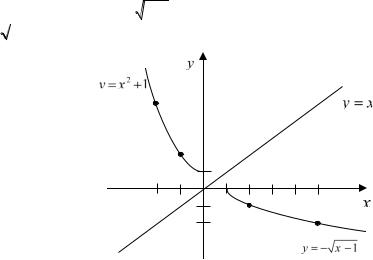
Задача. Найти функцию, обратную данной. Построить график

данной и обратной ей функций y x 2

1, x

;0 .

Решение

;0 D, E 1; .

y x 2 1, x

На промежутке ;0 функция y x 2

1 монотонно убывает.

Разрешим уравнение y x 2 1

относительно x , учитывая, что

x 0 , получаем

x

y 1 ,

переобозначим

переменные:

E ;0

y x 1, D 1;

,

–

обратная

функция для

функции y x 2 1, x

;0 .

5

1

0	1	5

Тема 2. ЭЛЕМЕНТЫ ТЕОРИИ ПРЕДЕЛОВ

Пределом функции в точке называется число, к которому приближаются значения функции при приближении аргумента к этой точке. Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл.

2.1. Предел последовательности

Последовательностью называется функция, определенная на множестве натуральных чисел . Значения этой функции

18

xn f (n) , , называются элементами или членами последовательности, число n называется номером элемента xn . Для последовательностей используется обозначение xn или более наглядная запись x1, x2 , x3 , , xn , . Задать последовательность можно с помощью формулы, связывающей n и xn .

Приведем примеры последовательностей, указав их различные

представления:
а)		1		, или 1,		1			1		,	1			,		или	1				;
	xn							,		,			,
						2			3			n
		n
																		n
б)	xn n			2 , или	1, 4, 9,						, n			2	,		, или		n		2	;
в)	xn 1 ( 1)n ,					или 0,					2, 0,	2,			0,	,		или			1 ( 1)n .

Заметим, что элементы этих последовательностей ведут себя поразному с увеличением номера n : в первом случае убывают, приближаясь к нулю; во втором случае неограниченно возрастают; в третьем случае не приближаются ни к какому определенному числу, принимая

поочередно значения 0 и 2 . Для описания поведения элементов последовательности при неограниченном увеличении n вводится понятие предела.

Число а называется пределом последовательности xn , если для
любого положительного числа	существует такой номер					n0 , что для
всех n n0 выполняется неравенство			xn a		(то есть	xn отлича-
ется от a менее, чем на ).
Если предел существует,	то говорят, что последовательность

сходится, и пишут lim xn		a (читается: ―предел xn равен a ‖) или
	n
xn a	при n (― xn	стремится к a при n , стремящемся к бес-

конечности‖). В противном случае говорят, что последовательность

расходится.

Примеры. а) Последовательность xn 1n сходится, ее предел

равен нулю: lim 1 0 . Это непосредственно следует из определения

n n

19

предела, поскольку при любом 0 неравенство

1

0

выполня-

n

ется для всех

n

1

, и в качестве

n

можно взять любое натуральное

0

число, большее

1

.

б) Аналогично доказывается более общее утверждение:

lim

1

0

при любом 0 .

n n

Например,

lim

1

0 , lim

1

lim

1

0

и т. д.

n n2

n

n

n n1/ 2

Правила вычисления пределов последовательностей

При вычислении пределов последовательностей используются следующие правила:

I. Если последовательности xn и yn сходятся, то сходятся

их сумма, разность и произведение, причем:
	1)	lim (xn yn ) lim xn lim yn ,
		n					n		n
	2)	lim (xn yn ) lim						xn lim yn ,
		n					n		n
	3) lim (xn yn )					lim xn lim yn ;
	n				n				n
если yn	0 и	lim yn	0 , то сходится также и частное:
	n
		4)		xn			lim x	n	.
			lim				n
			n yn				lim yn
							n
II. Предел последовательности							xn C , где C - постоянная,
равен этой постоянной:

lim C C .

n

III. Постоянный множитель можно выносить за знак предела:

lim (Cxn ) C lim xn (следствие правил I.3 и II).
n	n

Применению указанных правил часто предшествуют некоторые предварительные преобразования выражения, стоящего под знаком предела.

20