лекции мат. анализ

																																													1
														x				5		1													x			5		1						5										1													x			5				1										1			ln(x5							1) ln(5x 2) .
			y ln 5																				ln																																					ln
														5x 2																			5x																					5												5x							2								5
																																						2
		Тогда y																				ln x												1 ln 5x 2																																										1					ln x										1						ln 5x 2)							.
																															5																																																									5
																				1
																				5																																																									5
																																																																							5
		Для нахождения производных ln(x																																																																1) и ln(5x																									применим
																																																																																																		2)
																									U
формулу: lnU																																.
																									U
		Получим:
			1					(x5			1)										(5x 2)																				1				(x5 ) (1)																											5(x) (2)																				1			5x 4 0								5 0
y
										5																																											5																																												5
			5					x			1											5x 2																			5									x							1																			5x 2																5				x		1
																																																																																																						5x 2
	1					5x 4														5												x 4													1																			4x5								2x 4 1
																																																																																							.
							5																									5																																		5
	5							1																					x					1										5x 2																		(x							1)(5x 2)
		x															5x 2
																														1
Задача 3.											y arctg																											arccos																						x 2 .
																											x 2
Решение.
																		1																																																												1
y arctg																					arccos																				x				2																arctg																														arccos								x 2 .
														x 2																																																														x					2
		Для нахождения																																		производной																																			arctg										1										применим										формулу
																																																																																		x 2
																			U																																			1
arctg U																								. Здесь U																																									. Тогда
																1 U 2																																(x 2)
																																									1
																																																																																1
																				1																																																																							( 1)( x 2) 1 1
																																		x 2																															x 2
							arctg
																		x		2																														2																											1 2																				1 2
																																						1
																															1																															1																													1
																																						x								2																							x 2																									x			2
																				1																							1
															(x 2)2																									(x 2)2																																						1																				1					.
																	1							2											(x 2)2 1																																	(x 2)2 1																									x2 4x 5
								1
																																						(x							2)						2
																	x 2

31

		Для нахождения производной arccos
																																																									x 2											применим формулу
																																																																																													1
													U '																																																																											x 2 2
																																																											(							x			2)'
a rccos					U															. Тогда												arccos													x 2
																																																																																								1 x 2
												1 U 2																																													1 ( x 2)2
		1			x 2				12 1												1				x 2										1
																																																									1
																							2											2
				2																																																																						.
						x 1																				x 1																		2 ( x 1)( x 2)
		Следовательно, y																																1																										1																		.
																												x2				4x 5
																																																2				( x 1)( x 2)
		Задача 4.									y 6tg x											x2 cos 2x .
		Решение.								y 6								tg x					x				2																	6				tg x							x						2		cos 2x .
																														cos 2x
		Найдем: 6										tg x																											u							u	∙ln a∙U'.
														по формуле (a																										)'=a
																	tg x												tg x																										tg x														1
		Будем иметь 6																					6									ln 6(tg x) 6																										ln 6																									.
																																																																				cos 2 x
		Производную (х2cos2x)' найдем по формуле ( U · υ )' = U' υ + U υ ' и
(cosU)'=-sinU U'. Тогда
x	2													2	) cos 2x x																		2		(cos 2x) 2x cos 2x x																																							2			( sin 2x)(2x)
		cos 2x) (x
2x cos 2x 2x2 sin 2x 2x(cos 2x x sin 2x).
Следовательно,														y 6tg x ln 6																					1										2x(cos 2x x sin 2x) .
																																			cos 2 x
		Задача 5. Вычислить приближенное значение																																																																					5			252 ,												заменив в
точке х=243 приращение функции y 5
																																																		x						дифференциалом.
		Решение. Имеем:																					y dy,													т.е.										y 5										x							x 5								x .
		В нашем примере х =2 4 3 , х +∆ х =2 5 2 , тогда ∆ х =2 5 2 – 2 4 3 =9 ,
																														1												1						1		1											1					4																				1
												5																		5																		5																			5
		dy y dx												x dx x																						dx						5				x							dx								5		x						dx																						dx .
																																																																													5										x		4
																																																																													5
		Отсюда														y 5								252 5												243 5												243 9 5																		243 5 243 9 3,
dy					1							x									1											9								1						9											1										1			.
				55												5 5											4											5 34																5 32													45
					2434
																					243

32

Поэтому 5252 5243 451 .

Следовательно, 5252 5243 451 3 451 3,022 .

Тема 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ

Определение. Функция у = f ( x ) называется возрастающей в интервале (a , b), если при х 2 > х 1 , f ( x 2 ) > f ( х 1 ) , и убывающей, если

f ( x 2 ) < f ( х 1 ) .

Достаточные признаки возрастания и убывания функции:

если функция f(x) в каждой точке интервала (a , b) имеет положительную производную, то сама функция в этом интервале возрастает;

если функция f(x) в каждой точке интервала (a , b) имеет отрицательную производную, то функция в этом интервале убывает.

Определение. Функция у = f ( x ) имеет экстремум (максимум или минимум) в точке х = х0, если f ( x 0 ) является наибольшим или наименьшим значением функции в некоторой окрестности этой точки.

Необходимое условие экстремума функции

Если функция у = f ( x ) имеет экстремум в точке х = х0, то ее производная в этой точке равна нулю, либо не существует.

Значения аргумента, при которых функция f(x) сохраняет непрерывность, а ее производная f'(x) обращается в нуль или не существует,

называются стационарными или критическими точками.

Первый достаточный признак экстремума функции

Если функция у = f ( x ) дифференцируема в окрестности стационарной точки х0 и ее производная слева от этой точки положительная, а справа отрицательная, то в точке х0 функция достигает максимума; если производная слева от стационарной точки х0 отрицательная, а справа – положительная, то в точке х0 функция достигает минимума; если производная слева и справа от стационарной точки х0 имеет одинаковый знак, то в этой точке функция экстремума не имеет.

Второй достаточный признак экстремума Если в стационарной точке х0 вторая производная отлична от

нулю, то в этой точке функция у = f ( x ) имеет максимум при f''( x 0 )<0 и минимум при f''( x 0 ) >0 .

Определение. Кривая у = f ( x ) называется выпуклой на интервале (a , b), если при a < x < b она расположена ниже касательной, проведенной в любой точке интервала (a , b).

33

Определение. Кривая у = f ( x ) называется вогнутой на интервале (a , b), если при a < x < b она расположена выше касательной, проведенной в любой точке интервала (a , b).

Определение. Точки, отделяющие выпуклую часть непрерывной кривой от вогнутой (или наоборот), называются точками перегиба кривой.

Признаки выпуклости и вогнутости кривой.

Если вторая производная функции y''( x ) положительна во всех точках интервала (a , b), то на этом интервале график функции является вогнутым.

Если вторая производная функции y''( x ) отрицательная во всех точках интервала (a , b), то на этом интервале график функции является выпуклым.

Определение. Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном

удалении ее от начала координат.
	Если lim f (x) или			lim f (x) ,	то прямая х = а		является
		x a		x a
вертикальной асимптотой кривой у = f ( x ) .
	Прямая		у = b является	горизонтальной		асимптотой	кривой
у = f ( x ) , если существует предел lim f (x) b					или lim f (x) b .
				x		x
	Если			существуют			пределы
lim	f (x)	k	и lim f (x) kx b , то			прямая у=kx+b есть
x	x		x

наклонная асимптота кривой у = f ( x ) .

Для построения графика функции ее можно исследовать по следующей схеме:

1.Найти область определения функции, интервалы непрерывности и точки разрыва функции. Найти вертикальные асимптоты, исследуя изменение функции при х, стремящемся к точкам разрыва функции.

2.Исследовать функцию на четность, нечетность, периодич-

ность.

3.Найти точки экстремума и промежутки возрастания и убывания функции. Вычислить значения экстремумов.

4.Определить интервалы выпуклости и вогнутости графика, найти точки перегиба.

5.Найти горизонтальные и наклонные асимптоты кривой (если они существуют). Найти точки пересечения кривой с осями координат (если они существуют).

34

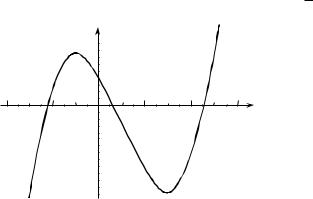
Пример. Исследовать функцию y	x3	x2 3x 2 и построить
3

ее график.

Решение. Функция у ( х ) точек разрыва не имеет. Область определения – вся числовая ось. Вертикальных асимптот нет. Горизонтальных и наклонных асимптот нет.

Исследуем данную функцию на экстремум. Определим критические точки. Для этого находим первую производную данной функции и приравниваем ее к нулю: y'=x 2 – 2 x – 3 , x 2 – 2 x – 3 =0 .

Решая последнее уравнение, находим его корни: х1 = – 1 , х2 = 3. Таким образом, х1 = – 1 и х2 =3 – критические точки. Так как производная f'( x ) существует при любом значении х, то других критических точек не имеется.

Исследуем критическую точку х = – 1. Производную y '( x ) представим в виде произведения двух сомножителей: y'=(x +1 )( x – 3 ). Из этого равенства видно, что при x<–1 производная f'( x ) положительная, а при – 1 < x <3 производная f'( x ) отрицательна. Следовательно, в интервале (–∞, –1) функция возрастает, в интервале (–1,3 ) – убывает, а в интервале (3,∞) - возрастает. Так как производная y' при переходе через критическую точку х=–1 меняет свой знак с плюса на минус, то в этой точке функция имеет максимум.

Аналогично исследуем точку х2=3. и убеждаемся, что в этой точке

функция имеет минимум. Найдем экстремум					ymax 3	2 ,	ymin 7 . Из
						3
		y			второй		производной
		4			y''( x )=2 x – 2			найдем
					точку х=1, подозри-
		2			тельную на точку пере-
					гиба. Так как при пере-
				x
					ходе	через эту		точку
–4	–2	2	4	6	y''( x )	меняет знак, то
					точка х=1 является точ-
		–2
		–4			кой перегиба. В интер-
					вале (–∞,1) график
		–6			функции		является вы-
					пуклым,		так	как
					y''( x )<0 ; в интервале
(1,+ ∞) – график вогнут, так как y''( x ) >0 . Строим график.

35

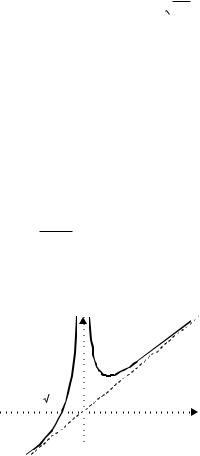
Пример. Исследовать функцию	y	(x3		4)		и построить ее гра-
			x2
фик.
Решение. Найдем производные:	y		(x3	8)		; y	24	.
			x3
							x4

Область определения D( y) ( ,0) (0, ) .

Свойствами четности, нечетности функция не обладает. График

пересекается с осью Ох в точке x 3 4 . Критические точки: х=2, х=0. Последняя не входит в область определения, поэтому ее не рассматриваем. Найдем у(2)=3 и нанесем точку (2,3) на плоскость Оху.

Исследуем поведение у в окрестности точки х =2 . При 0<х <2 , y'<0, при х >2 , y'>0. Следовательно в точке х=2 функция имеет минимум. На промежутке (–∞,0) y' >0 , следовательно функция возрастает. Исследуем направление выпуклости графика. Всюду y'' >0 , следовательно точек перегиба нет и кривая всюду вогнута. Исследуем функцию вблизи точки разрыва непрерывности х =0 и при х →∞ , х → – ∞ :

	lim		x3	4	, lim		x3	4	, lim	x3	4	, lim	x3	4	.
			x	2			x	2		x	2		x	2
	x	0			x	0			x			x

Прямая х=0 – вертикальная асимптота. Найдем наклонную асимптоту y=kx+b:

k lim x3 4 1,

x x2 x

x3 4					x3 4 x3			4
b lim			x	lim			lim			0.
	x	2			x	2			2
x				x			x x

Получим наклонную асимптоту у=х. Строим график функции.

	8	y
	6
	4
	2			x
	3 4
-4	-2	0 2	4	6

36

x 2 + y 2 = a

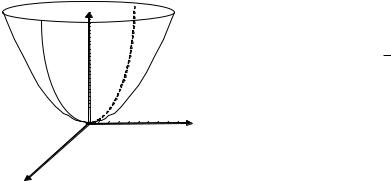
Тема 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Многим экономическим явлениям присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных.

5.1. Основные понятия

Определение. Переменная z называется функцией переменных х и у, если каждой паре значений х и у в некоторой области их изменения поставлено в соответствие одно значение z. Функциональную зависимость z от х и у записывают в виде: z = f ( x , у) . Это уравнение определяет некоторую поверхность в пространстве R3.

Определение. Графиком функции двух переменных

называется множество		точек пространства	аппликата
которых связана с абсциссой		и ординатой функциональным соот-
ношением	. График функции двух переменных		,

вообще говоря, представляет собой некоторую поверхность в трехмерном пространстве.

	Определение. Линией уровня функции двух переменных
	называется множество точек на плоскости, таких, что во
всех этих точках значение функции одно и то			же и равно		, то
есть	.
	Геометрическим образом функции z = x 2 + y 2 является параболо-
		ид. Пусть z = a, тогда x 2 + y 2 = a ,
	z	т.е. линия	пересечения		плос-
		кости z=a	с	поверхностью
		z = x 2 + y 2	есть	окружность

z x 2 y 2

0 y

x

радиуса R a . Пусть у=0, тогда z=x2 и, следовательно, при пересечении плоскости Oхz с поверхностью получается парабола. Метод сечений дает возможность лучше представить себе геометрический образ данной функции.

37

Определение. Число А называется пределом функции z = f ( x , у) в точке М0(х0, у0), если для каждого числа ε>0 найдется такое число β>0 , что для всех точек М(х,у), для которых выполняется неравенство |ММ0|<β, будет выполняться неравенство |f ( x , у ) – A |< .

Обозначим lim f (x, y) A .

x x0 y y0

Определение. Функция z = f ( x , у) называется непрерывной в

точке М0(х0,у0), если имеет место равенство lim f (x, y) f (x0 , y0 ) .

x x0 y y0

5.2. Частные производные и полный дифференциал 1-го порядка

Определение. Производная от функции z = f ( x , у) по х, найденная в предложении, что у остается постоянным, называется частной

производной от z по х и обозначается z или f' x ( x , у) . Аналогично

x

определяется и обозначается частная производная z по у.

Если функция z = f ( x , у) имеет в точке (х,у) непрерывные частные производные, то ее полное приращение может быть представлено в виде:

z

z

x

z

y ,

(1)

x

y

где 0

при

x 2

y 2

0 .

Определение. Выражение

z

x

z

y является главной ча-

dx

dy

стью полного приращения z и называется полным дифференциалом функции z = f ( x , у) и обозначается d z:

	dz	z	x	z	y .
		x		y

Полагая в формуле (2) z равным х, найдем dy y . Поэтому

dz dxz dx dyz dy .

(2)

dx x , а при z=y

(3)

Из (1) следует, что z dz .

Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.

38

z

z

y

Задача.			Найти	полный	дифференциал	функции
5x2 6y 3x2 y3 .
Решение. Сначала найдем частные производные
	z	5x2	6 y 3x2 y3	x 10x 0 3 2xy 3 10x 6xy 3 ,
	z
	z	5x2	6 y 3x2 y3	y 0 6 3x2 3y2 6 9x2 y2 .
	y

Производная z найдена в предположении, что у постоянна, а

x

найдена в предположении, что х постоянна. По формуле (3):

dz xz dx yz dy (10x 6xy 3 )dx (9x2 y2 6)dy .

Ответ –

5.3. Градиент функции. Производная по направлению

Определение. z = f ( x , у) дифференцируемая функция двух пере-

менных. Тогда вектор gradz

z

i

z

j

называется градиентом

x

y

функции z = f ( x , у) .

Он обладает следующими свойствами:

gradC 0,

c const,

grad(U ) gradU grad ,

grad (CU ) CgradU , C const,

grad (U ) gradU Ugrad ,

grad

U

gradU Ugrad .

2

Пусть

cos ,

cos – направляющие косинусы некоторого век-

тора , т.е.

cos i cos j . Тогда

z

z

cos

z

cos – про-

x

y

изводная функции z = f ( x , у) в данном направлении .

39

5.4. Экстремум функции двух переменных

Определение. Функция z = f ( x , у) имеет в точке М0(х0,у0) максимум, если в окрестности этой точки выполняется равенство

f ( x , у) < f ( x 0 , у0 ) .

Аналогично определяется минимум функции z = f ( x , у) в точке

М0(х0, у0).

Необходимый признак экстремума

Если М ( х 0 , у 0 ) – точка экстремума дифференцируемой функции z = f ( x , у) , то

	f (x0 , y0 ) 0		и		f (x0 , y0 )	0, то есть df (x	, y ) 0.
	x				y	0	0
	Достаточный признак экстремума
	Пусть z = f ( x , у) – функция, для которой существуют производ-
ные	первого	и второго			порядка	в точке М ( х 0 , у 0 ): A		f (x , y ),
								xx 0 0
B	f (x , y ),	C	f	(x , y ) . Составим выражение			= А С – В 2 .
	xy 0 0		yy	0	0

Если Δ>0, то М(х0, у0) – точка экстремума, а именно: точка максимума при A<0 (если C<0), точка минимума при A>0 (или С>0). Если Δ<0, то в точке М нет экстремума.

Задача. Исследовать на экстремум заданную функцию.

Решение. Находим частные производные:

;

Воспользовавшись необходимым условием экстремума, находим стационарные точки. Для этого решаем систему уравнений:

	{	{
откуда		Таким образом, стационарной является
точка	. Находим значения частых производных второго порядка
в точке :
Составляем выражение:
Так как	делаем вывод о наличии минимума в точке
. При этом минимальное значение функции			.

40