ves_sopromat

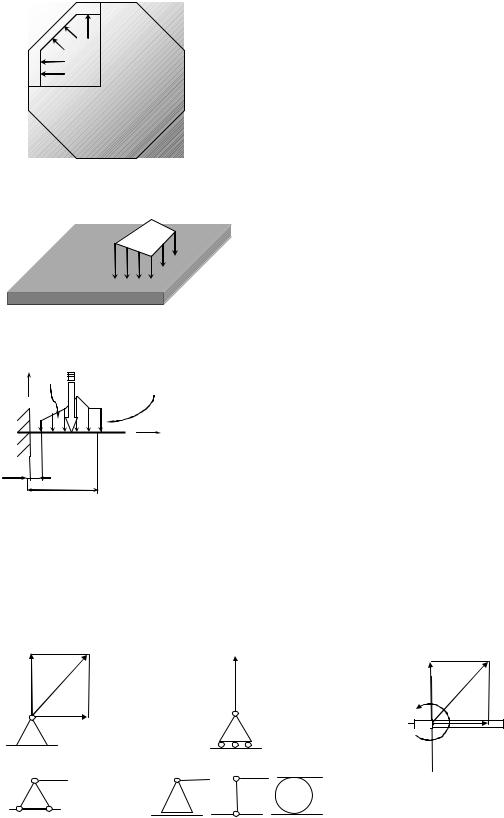
-11 -

распределенные, которые можно подразделить следующим образом: o объемные, [Н/м3],

p	Примером	действия	объемной
	распределенной	нагрузки	является
	давление жидкости или газа на
	внутреннюю поверхность сосуда.

o поверхностные, р [Н/м2] = [Па],

p

Примером действия поверхностной распределенной нагрузки может быть действие снеговой нагрузки на крыши домов.

o линейные, q [Н/м];

		P
y		q z
		z

a

b

Примером действия линейной распределенной нагрузки может быть нагрузка на балочные перекрытия.

b

P q z dz - площадь фигуры,

a

ограничивающей влияние распределенной нагрузки.

по возникновению:

активные (силы P [H] и моменты M [H м]);

реактивные (реакции опор).

Основные опоры и их опорные реакции имеют вид :

yA		R = yA	yA	R
	R	A	MA
A

xA	A	xA
	жесткая заделка

цилиндрическая	цилиндрическая
шарнирно-	шарнирно-
неподвижная	подвижная
опора	опора

- 12 -

Для проведения расчетов на прочность необходимо знать внутренние усилия, которые определяются с помощью метода сечений.

Метод сечений представляет собой алгоритм из четырех действий:разрезаем брус плоскостью, перпендикулярной его оси

P1
левая половина	Pn

правая половина

Pi

		ось бруса
P2	P3

плоскость, перпендикулярная P4

оси бруса

отбрасываем ту часть бруса, которая содержит большее количество неизвестных

		A	A	Pn
	P1
P2
		PA	PA
				Pi
	P3
				P4

заменяем действие отброшенной части равнодействующими усилиями.
			y			R - главный вектор системы внутренних сил;
M y
						M - главный момент системы внутренних сил;
						N - нормальная (продольная) сила;
Qy
			R			Q ,Q			- поперечные силы;
				M				y
						x
						M z
Qx				z			- крутящий момент;
					M z	M x	, M y - изгибающие моменты.
x	M x			N

Перечисленные силы и моменты являются внутренними силовыми факторами.составляем уравнения равновесия для определения внутренних силовых

факторов (сил и моментов):

n

n

n

N Piz 0;

Qx Pix 0;

Qy Piy 0;

i 1

i 1

i 1

n

0; M

n

0; M

n

0.

M

k

m

P

x

m

P

y

m

P

0z

i

0x

i

0y

i

i 1

i 1

i 1

-13 -

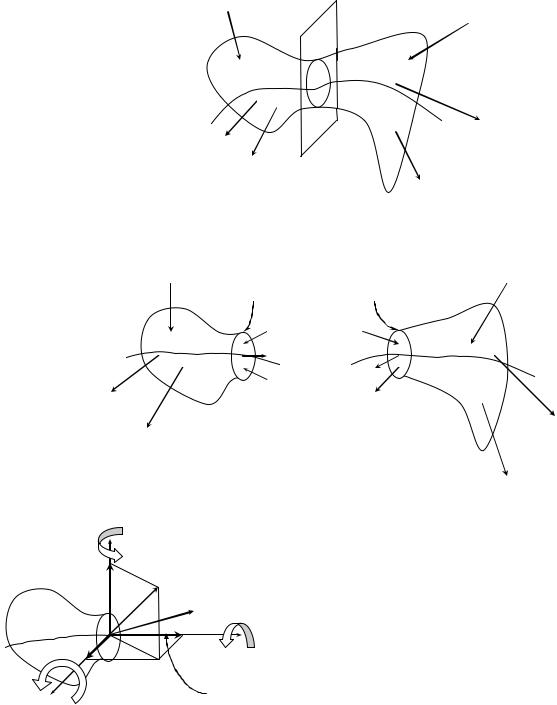
Втеоретической механике доказывается теорема Пуансо:

всякую систему сил относительно любой точки можно привести к эквивалентной системе, состоящей из главного вектора и главного момента, выходящих из этой точки.

	Р1				M0
О		Р2		О
Рn				Р0
Для того, чтобы система находилась в состоянии равновесия, необходимо и
достаточно, чтобы главный вектор		Ro		и главный момент	M	o были равны нулю:

Ro 0 : { Rox= 0; Roy= 0; Roz= 0},

Mo 0 : {Mox= 0; Moy= 0; Moz= 0}.

§5. Напряжения, перемещения, деформации.

Напряжением называется интенсивность внутренней силы в данной точке

поперечного сечения. Размерность напряжения:

p

Н

Па

м

2

y

y

zy

p

dQy

dR

dF

dQx

dF

zx

x

dN

x

z

z

z

n

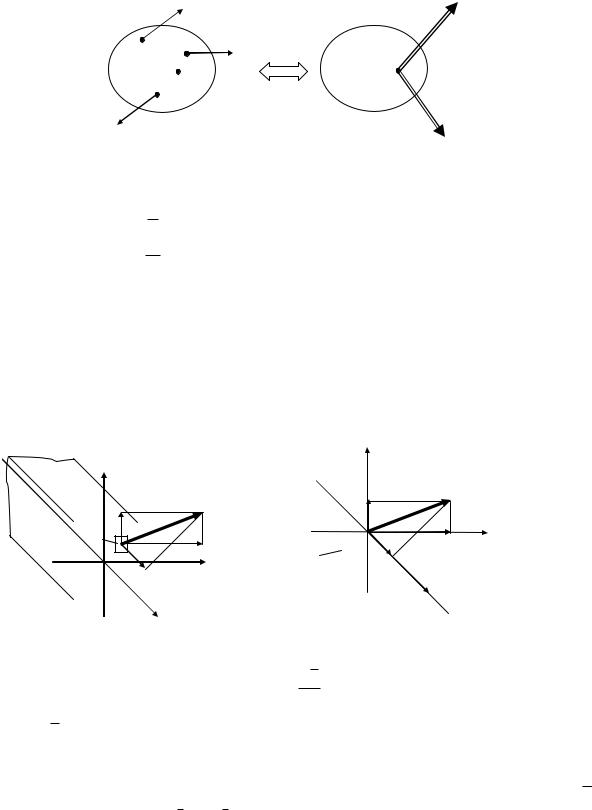
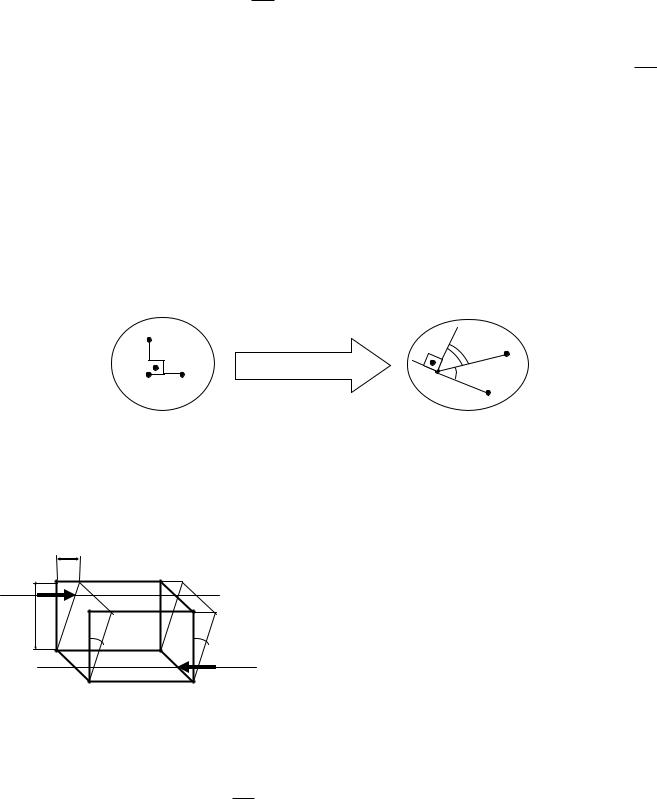
Полным напряжением в точке называется векторная величина:

p lim dR ,

dF 0 dF

где: dR - равнодействующая сил;

dF - элемент площади поперечного сечения.

Разложим полное напряжение p на нормальное напряжение z и

касательные напряжения zx и zy .

Полное напряжение в точке определяется по формуле:

- 14 -

p z2 zx2 zy2

Несложно установить зависимости между напряжениями и внутренними силовыми факторами:

N dF ;

	F
Qx	zxdF ;
	F
Qy	zy dF ;
	F
M x	y z dF ;
	F
M y	x z dF ;
	F

M z ( y zx x zy )dF dF ,

F F

где: ρ – полярный радиус (кратчайшее расстояние от точки приложения силы до центра тяжести сечения); x2 y2 ;

dQ

dQy 2

dQx 2

2

2

- полное касательное напряжение;

zy

zx

.

dF

dF

dF

Замечание: направление действия напряжений всегда совпадает с направлением действия вызывающих их сил.

Совокупность напряжений для множества площадок, проходящих через данную точку, образуют напряжѐнное состояние в точке.

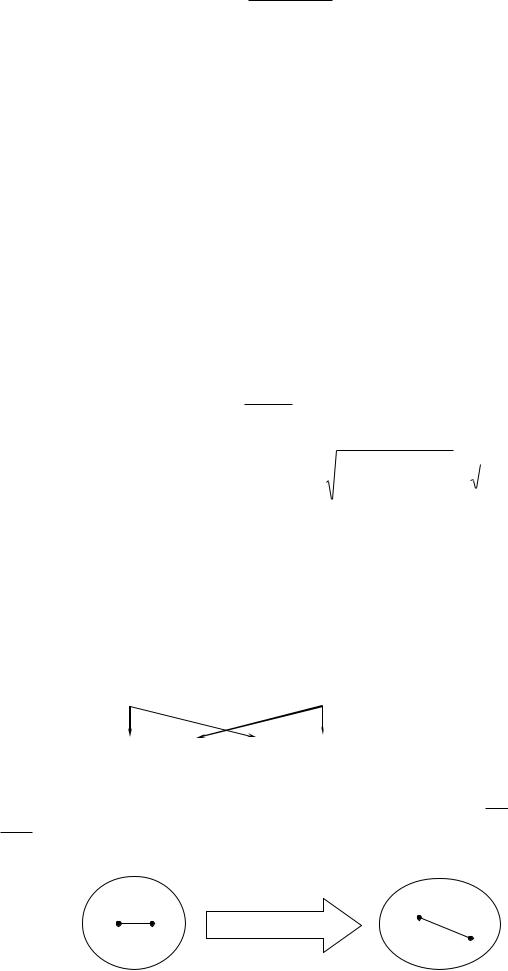
Под действием внешних сил тело деформируется, т.е. изменяет свои размеры и форму, в результате чего в нем могут возникать следующие виды деформаций.

Линейные		Угловые
Абсолютные		Относительные

Рассмотрим линейные абсолютные и относительные деформации.

Пусть в некотором теле после деформации внутренний отрезок AB переходит в

отрезок A' B'.

	A	A	B
	деформация
	B

- 15 -

Абсолютной линейной деформацией l называется разность между конечной

lк и начальной длиной lн отрезка AB :

l lк lн = А В АВ .

Относительной линейной деформацией в точке А по направлению AB

называется безразмерная величина, равная:

	εAB lim	A' B' AB
		AB
	AB 0

Относительные линейные деформации вдоль координатных осей x, y, z обозначаются x , y , z .

Примером линейных деформаций могут служить деформации колонн, штоков поршневых машин и т.п. при их работе.

Рассмотрим абсолютные и относительные угловые деформации.

Пусть прямой угол DOC внутри тела после деформации переходит в угол

D'O'C'.

D

DOC

	деформация		D
O	C	O	C

Абсолютной угловой деформацией (углом сдвига) в точке О в плоскости

DOC называется безразмерная величина, равная:
DOC	lim	DOC D'O'C' .
	DO 0,CO 0

В координатных плоскостях xy, xz, yz углы сдвига обозначаются xy , xz , yz .

S

a

P

	Для	лучшего	понимания		можно
	рассмотреть	возникновение		абсолютной
	угловой деформации при смещении двух
	параллельных плоскостей друг			относительно
P	друга под действием поперечной силы Р.

Относительной угловой деформацией (относительным сдвигом) называется отношение абсолютной угловой деформации к расстоянию между сдвигающимися плоскостями:

aS , т.к. 0 , то tg .

Примерами возникновения угловых деформаций могут служить деформации болтов и заклепок при их работе.

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки определяют деформированное состояние в точке.

Деформированное состояние точки тела полностью определяется 6 -ю компонентами деформации:

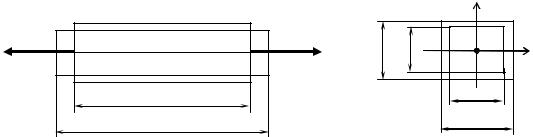
	- 16 -
Линейные		Угловые
( εx; εy; εz )		( γxy; γyz; γxz )

Перемещения являются абсолютными величинами, выражаемыми в единицах длины или в радианах ( l , f, , ).

Деформации -		относительные величины, выражаемые в процентах или
безразмерные (	lк	lн	100% ,	l	).
		lн		l

Систему, в которой внутренние усилия, напряжения, деформации и перемещения прямо пропорциональны действующей нагрузке, называют линейно-

деформируемой.

Для выполнения этого условия требуется, чтобы материал конструкции работал как линейно-упругий, т.е. чтобы его диаграмма деформирования была линейной. Такие системы называют физически линейными.

Требуется также, чтобы возникающие в конструкции при деформировании перемещения были достаточно малыми, по сравнению с ее размерами, и их можно было бы не учитывать в расчетной схеме. Такие системы называют геометрически линейными.

§6. Центральное растяжение - сжатие. Закон Гука.

Центральное растяжение-сжатие – такой вид деформации бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор, отличный от нуля – нормальная (продольная) сила N, приложенная в центре тяжести поперечного сечения бруса.

Если N действует от сечения, то она вызывает растяжение (увеличение длины бруса) и считается положительной (N > 0 – растяжение).

Если N действует к сечению, то она вызывает сжатие (уменьшение бруса) и считается отрицательной (N < 0 – сжатие).

Брусья, в основном работающие на растяжение-сжатие, называются

стержнями.

Рассмотрим центральное растяжение стержня.

Р	Р
	l
	l+ l

	y
a a- a	x
	b- b
	b

-17 -

ε= Δll - относительная продольная деформация;

εx = Δbb ; εy = Δaa - относительная поперечная деформация.

Экспериментально доказано, что при центральном растяжении-сжатии горизонтальная и вертикальная относительные поперечные деформации равны, т.е.

εx = εy = ε .

Отношение поперечной деформации к продольной деформации – величина постоянная для любого материала и еѐ абсолютное значение называется

коэффициентом Пуассона.

Эта величина безразмерна и определяется экспериментально. В зависимости от пластических свойств, для изотропных материалов имеем:

0 0,5 .

Пример:	μ пробки = 0;
	μчугуна = 0,23 ÷ 0,27;
	μстали = 0,29 ÷ 0,33;
	μмеди = 0,31 ÷ 0,33;
	каучука = 0,47.

Чем выше пластичность материала, тем больше его коэффициент Пуассона. Для большинства металлов в области действия закона Гука коэффициент Пуассона лежит в пределах 0,25 0,35 .

Для большинства материалов с достаточной точностью можно сказать, что: в

упругой области нагружения существует прямая пропорциональная зависимость между относительной линейной деформацией и нормальны м напряжением. Это положение называется законом Гука и выражается формулой:

σ = Еε ,

	где: Е – модуль	продольной упругости (модуль упругости первого рода,					модуль Юнга),
	справочная величина, для каждого материала своя и неизменна;		Е	Н				Па .
					м	2
	Пример:	Ест али = 2 105 МПа;
		Еалюминия = 0,8 105 МПа.

Впервые эту зависимость установил английский ученый Роберт Гук в 1756г. Первоначальная трактовка закона следующая: какова сила, такова и деформация.

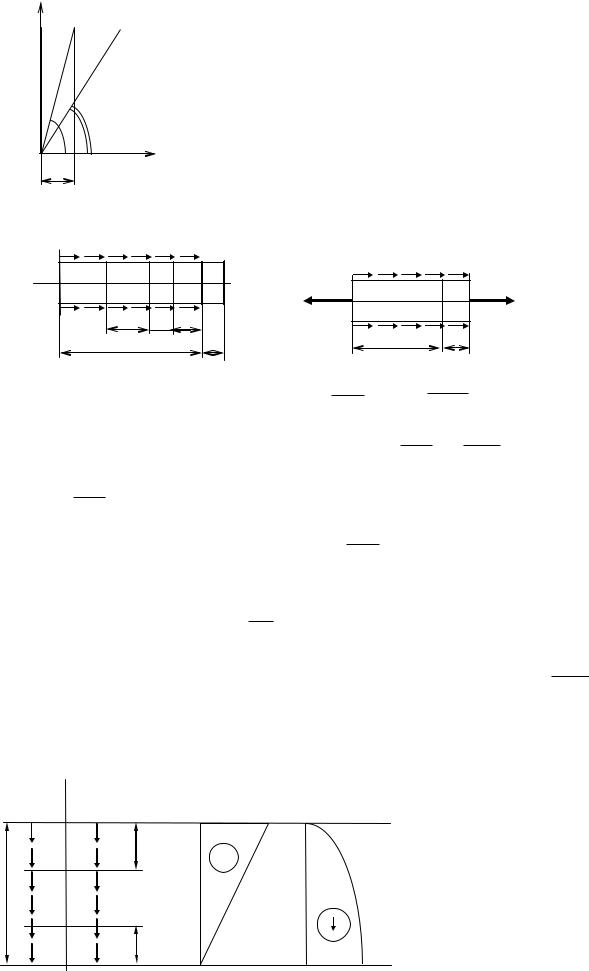
- 18 -

1

1 – сталь;

2

2 – алюминий.

Экспериментально показано, что стали = 0,002.

1

2

Чем пластичнее материал, тем меньше угол .

0,002

Выведем формулу Гука из одноименного закона.

q

q

N(z)

N(z)

dz

(dz) z

l

l

dz

(dz)

Для участка длиной dz имеем:

σ

N z ,

ε

dz

;

F

dz

Подставим эти соотношения в закон Гука:

N z E

dz ,

F

dz

l

l

N z dz ;

dz

откуда

получаем

формулу

Гука

для

стержня

с

0

0

EF

N z dz .

распределенной нормальной нагрузкой : l

z

EF

Несложно заметить, что если нормальная нагрузка постоянна, то формула

Гука примет следующий вид: l

Nl .

EF

Для стержня, имеющего n различных участков, получаем:

l

n

N z

i

dzi

E F

i 1

i i

Произведение EF называется жесткостью материала.

Пример: определить удлинение стержня l, вызываемое действием собственного веса q.

			N
						0 z l	0 z l
		z	ql			N(z) = ql ,	N(z) = ql-qz ,
			+			N(0) = 0 ,	N(0) = ql ,
l						N(l) = ql .	N(l) = 0 .
		q
					ql2
		z			2EF

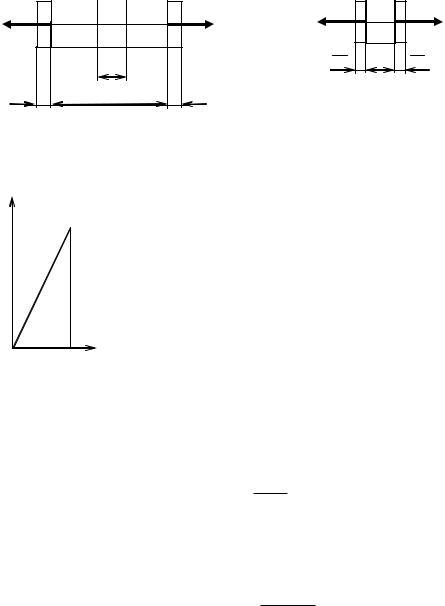
- 19 -

l N( z )

l ql qz

ql 2

ql 2

ql 2

l

dz

dz

.

0

EF

0

EF

EF

2EF

2EF

Ответ : l

ql 2

.

2EF

§7. Потенциальная энергия упругой деформации стержня при растяжении-сжатии.

Тело, находящееся под действием внешних нагрузок (системы сил, температуры и т.п.), испытывает напряженно-деформированное состояние. При освобождении тела от их действия оно совершит работу А, численно равную энергии упругих деформаций и вернет свои первоначальные форму и размеры.

Стержень длиной l увеличит свою длину на l, а элемент dz увеличит свою длину на dw.

N		N

l	dz	l
2	l	2

N		N

dw	dz	dw
2		2

Поскольку связь между напряжением и деформацией линей на (согласно закону Гука), то, очевидно, что связь между силой N и изменением длины dw тоже будет линейна.

N

							dU – площадь
							треугольника
						dw
dU	1		N	Ndz			N 2dz
								, тогда
	2			EF			2EF

	dU	1	Ndw ,	(1).
		2

По аналогии с формулой Гука для постоянной нагрузки N, имеем:

	dw	Ndz		,	(2).
		EF

Подставив (2) в (1), получаем:

l	N 2		N 2l
U		dz		.
	2EF		2EF
0

Итак, получена формула для определения потенциальной энергии упругой деформации стержня при растяжении-сжатии постоянной нормальной силой:

N 2l U 2EF .

Если нормальная сила не постоянна по длине стержня, то есть

N N z const, то работа, а, следовательно, и потенциальная энергия, опред еляются по формуле:

A U N 2 z dz . z 2EF

- 20 -

§8. Статически неопределимые системы при растяжении-сжатии. Температурные и монтажные напряжения.

Статически неопределимой называется система, в которой все внутренние силовые факторы не могут быть определены с помощью основных уравнений равновесия (уравнений статики).

Степень статической неопределимости определяется разностью между числом неизвестных (реакций опор или заделок) и числом основных уравнений равновесия. Для плоской системы таких уравнений может быть не более 3-х, для пространственной – не более 6-ти.

Для решения статически неопределимых задач необходимо составить столько дополнительных уравнений, сколько раз система статически неопределима. Эти уравнения называются уравнениями совместности деформаций.

Составление основных уравнений равновесия является статической стор оной решения задачи.

Составление дополнительных уравнений совместности деформаций является геометрической стороной решения задачи.

По ходу совместного решения составленных уравнений определяются все неизвестные, что является физической стороной решения задачи.

Пример. Определить опорные реакции и напряжения в стержне с двухсторонней жесткой заделкой.

l

l

Основное уравнение равновесия:

RA=

P

Fi(z) = RA – P + RB = 0 .

3

N

Система

один

раз статически

A

P

P

неопределима.

I

F

+

3

+

3F

Дополнительное

уравнение

II

P

2F

-

-

совместности деформаций:

P

2P

lI +

lII = 0 ,

B

3F

3

RAl

( RA P )l

0 ,

2P

RB=

EF

2EF

3

RA

RA

P

,

RA

P

, RB

2P

.

2

2

3

3

Положительные величины опорных реакций свидетельствуют о правильности выбора их начальных направлений.

Согласно формуле для опред еления нормальных напряжений при растяжении-

сжатии NF , получаем: