ves_sopromat

- 51 -

M

dF

G

d

2dF G

d

2dF G

d

J ,

dz

dz

z

dz

p

F

F

F

d

M z

.

dz

GJ p

Жесткостью сечения круглого бруса при кручении называется величина GJ p .

Размерность: GJ

p

Н м2 .

Поэтому: G

d

G

M z

M z

,

dz

GJ p

J p

M z

.

J p

Максимальные касательные напряжения при кручении будут возникать на

наружной поверхности вала, т.е. при m ax , следовательно:

M z max

M z

.

max

J p

W

Угол закручивания вала определяем по формулам Гука для кручения:

для вала с крутящим моментом M z

M z z const:

M z

z

dz

,

GJ

z

для вала с крутящим моментом M z

const :

M zl

.

GJ

§21. Расчеты на прочность и жесткость при кручении.

Расчеты на прочность.

а) проверочный расчет проводят с целью определения максимальных касательных напряжений при кручении и сравнения их с допускаемыми:

max M z

W

Для стали: 0,55 0,6 р ; Для чугуна: 1,0 1,2 р .

Расчеты ведутся с точностью до 5% от .

б) проектировочный расчет диаметра вала при кручении проводят по формулам:

W	M z	max	,		d		16M	z		.
						3

в) проектировочный расчет допускаемого крутящего момента проводят по формуле:

M z W d 3 .

16

- 52 -

Расчеты на жесткость.

а) проверочный расчет проводят из условия жесткости при кручении:

M z ,

GJ p

где: допускаемый относительный угол закручивания.

Размерность:		град				рад		м 1 .
		м				м
0,25 1,0м 1 .

б) проектировочный расчет по подбору диаметра вала проводят по формулам:

J	M zmax	,		d 4		32M zmax		.
	G					G

в) проектировочный расчет допускаемого крутящего момента проводят по формуле:

M z GJ G 32d 4 .

§22. Сдвиг и смятие.

Сдвигом называется такой вид деформации бруса, при котором в любом его поперечном сечении возникает только один внутренний силовой фактор – поперечная сила (Qy или Qx).

				Р
				z z		Qy	Примером сдвига является резка ножницами
							металлических полос и прутков.
				F			Qy dF F
							F
Р					P

При сдвиге в поперечном сечении бруса возникают только касательные напряжения, которые определяют по формуле:

QFy ,

где: Qy поперечная сила, F площадь сдвига.

- 53 -

Отметим, что вектор касательных напряжений лежит в плоскости площади сдвига F .

Условие прочности при сдвиге имеет вид :

QFy ,

где: допускаемое напряжение при сдвиге.

Плоское напряженное состояние, при котором в окрестности точки мо жно выделить элементарный (бесконечно малый) квадрат, на сторонах которого действуют только касательные напряжения, называется чистым сдвигом.

	Закон Гука при сдвиге имеет тот же вид, что и при кручении:								G ,
где:	касательное напряжение,
	G модуль сдвига,
	угол сдвига.
	Отметим, что существует связь между тремя упругими константами для любого
материала:		G	E		,
			2(1 )
где:	E модуль Юнга,

коэффициент Пуассона.

Сдвиг, приводящий к разрушению материала, называется срезом (при пластической деформации) и скалыванием (при хрупком разрушении).

Отметим, что допускаемое напряжение на срез для болтов ср 0,25 0,35 T , где: T предел текучести материала.

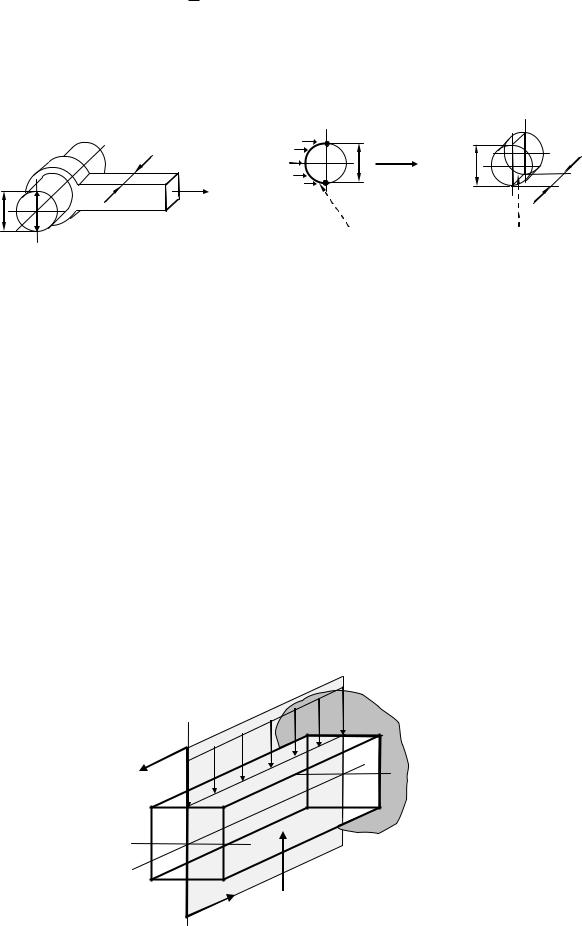
Смятие – деформация, обусловленная местным сжатием материалов соприкасающихся деталей по площадкам передачи давления.

Примером смятия является разрушение болтов или деталей, которые они соединяют, при чрезмерном закручивании гайки.

Р

болт

гайка

шайба

см

поверхность

Условие прочности при смятии имеет вид :

- 54 -

			P			,
	см				см
			Fсм
где: Р сжимающая сила,

Fсм площадь смятия,

см допускаемое напряжение при смятии.

Отметим, что вектор см направлен под углом (часто перпендикулярен) к плоскости смятия Fсм .

При контакте двух деталей по цилиндрической поверхности вводится условная

площадь смятия Fсм d , где:	d диаметр цилиндрической поверхности,
толщина соединяемой детали.

		d	Р	d
	Р
d	d
	тяга
		действительная			условная
		площадь			площадь
		смятия			смятия
	§23.	Прямой изгиб.

Изгибом называется вид деформации, при котором искривляется продольная

ось бруса.

Прямые брусья, работающие на изгиб, называются балками.

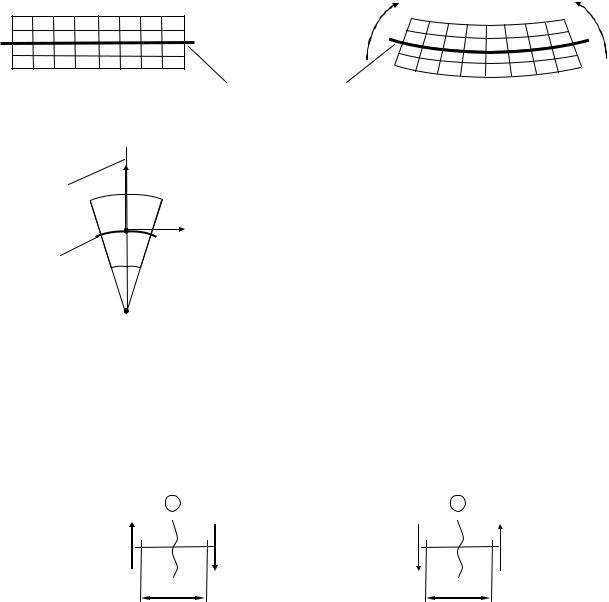
Прямым изгибом называется изгиб, при котором внешние силы, действующие на балку, лежат в одной плоскости (силовой плоскости), проходящей через продольную ось балки и главную центральную ось инерции поперечного сеч ения.

Изгиб называется чистым, если в любом поперечном сечении балки возникает только один изгибающий момент ( M x или M y ).

Изгиб, при котором в поперечном сечении балки одновременно действуют изгибающий момент и поперечная сила ( M x и Qy или M y и Qx ), называется

поперечным.

Линия пересечения силовой плоскости и плоскости поперечного сечения называется силовой линией.

		y
		qy
		Mx
	x
	z	Qy	силовая
			плоскость

- 55 -

Основные гипотезы при прямом изгибе: гипотеза о ненадавливании продольных волокон и гипотеза плоских сечений (гипотеза Бернулли).

Возьмем прямой брус и приложим к его свободным торцам два одинаковых по модулю, но противоположно направленных изгибающих момента M x . Пусть эти моменты изгибают брус выпуклостью вниз. Тогда снизу образуются растянутые продольные волокна, а сверху – сжатые продольные волокна. Между ними будет расположен слой продольных волокон, которые искривляются, но не меняют своей длины. Этот слой называется нейтральным слоем.

брус до		брус после деформации
деформации
		сжатые
	Mx	волокна	Mx

нейтральный слой	растянутые
	волокна

	y		Нейтральной линией (осью) называется линия
силовая			пересечения нейтрального слоя с плоскостью поперечного
линия
			сечения балки.
О		x
			При прямом изгибе декартова прямоугольная система
нейтральная			координат Oxyz выбирается таким образом, чтобы ось z
линия			была направлена по касательной к продольным волокнам
			нейтрального слоя, ось y вертикально вверх, а ось x -
			горизонтально слева направо.

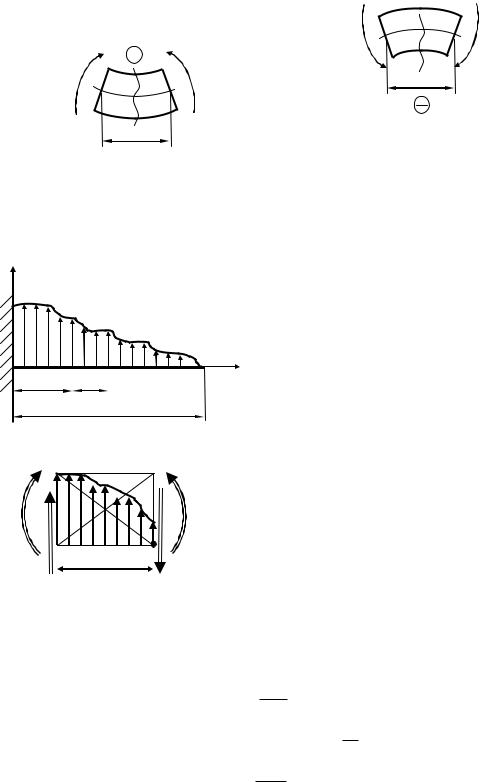
Правила знаков.

Поперечная сила Qy z считается положительной, если она стремится

повернуть элемент бруса dz по						часовой стрелке; и		отрицательной – против
часовой стрелки.
Qy(z)					Qy(z)	Qy(z)				Qy(z)
	dz							dz

- 56 -

Изгибающий момент M x z считается положительным, если он стремится

изогнуть элемент бруса dz выпуклостью вниз, при этом сжатые волокна расположены сверху; и отрицательным – выпуклостью вверх, при сжатых волокнах снизу.

сжатые

волокна

Mx(z) Mx(z)

dz

Mx(z)

Mx(z)

dz

сжатые

волокна

Примечание. Эпюра изгибающего момента всегда строится на сжатом волокне.

§24. Дифференциальные зависимости при изгибе.

y

qy(z)

z	dz	z

l

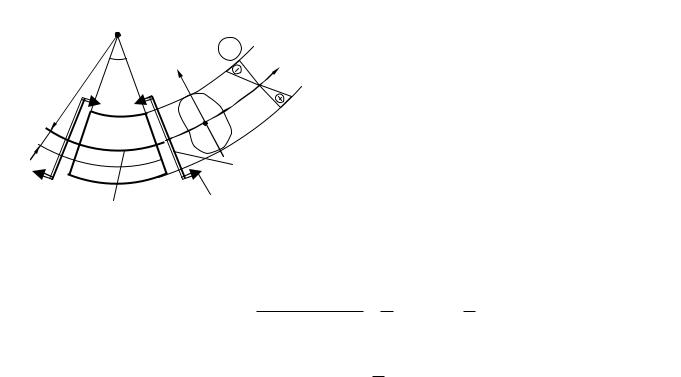
Рассмотрим консольную балку с неравномерно распределенной поперечной нагрузкой qy(z). На расстоянии z от заделки выделим элементарный участок dz.

Mx	qy(z)	Mx+dMx

Qy	dz	А	Qy +dQy

Мысленно отбросим левую и правую части балки от элемента dz и заменим их действие внутренними силовыми факторами. Пусть поперечные силы и изгибающие моменты на левом и правом торцах элемента бруса положительны.

Составим основные уравнения равновесия элемента бруса относительно точки

А:

FÀy 0 : Qy qy z dz Qy dQy 0, dQdzy qy z .

M Àx 0 : M x Qy dz qy z dz dz2 M x dMx 0, dMdzx Qy z .

Полученные дифференциальные зависимости называются теоремой Журавского: полная производная от изгибающего момента по z равна поперечной

- 57 -

силе; полная производная от поперечной силы по z равна интенсивности распределенной нагрузки.

Следствия:

вторая производная от изгибающего момента, взятая по длине, равна интенсивности распределѐнной нагрузки:

		d 2 M x		q	z ;
		dz	2	y
зависимости между qy(z), Qy	и Mx можно представить в интегральной форме:
Qy qy	z dz ,				M x Qy dz
z					z

они применяются для определения поперечной силы и изгибающего момента при любом способе задания распределенной нагрузки.

Дифференциальные зависимости при изгибе применяются для контроля правильности построения эпюр поперечных сил и изгибающих моментов.

§25. Нормальные напряжения при изгибе. Формула Навье.

Возьмем бесконечно малый элемент бруса dz с поперечным сечением A , к торцам которого приложены положительные изгибающие моменты M x (z) . Тогда

элемент бруса изогнется выпуклостью вниз. Внизу элемента бруса будут расположены растянутые продольные волокна, а сверху – сжатые продольные волокна. Между ними будет находиться нейтральный слой, продольные волокна которого искривились, но не изменили своей длины.

Пусть

радиус

кривизны

z

нейтрального

слоя,

d

угол,

z

образованный

линиями

торцов

элемента

y

z

балки.

Для

продольных

волокон

d

min

zmax

нейтрального

слоя

dz d .

Выберем

y

декартову

прямоугольную

систему

координат, ось z которой

направлена

плечо

вдоль продольных волокон нейтрального

Mx(z)

Mx(z)

сила

слоя,

ось

y

направлена

вертикально

нейтральный

вверх,

а ось x

касается нейтральной оси и

слой

направлена от нас.

Рассмотрим относительное удлинение продольных волокон

на расстоянии y

от нейтрального слоя

l y d d y

,

y .

l

d

Согласно закону Гука, нормальные напряжения равны :

z Е E y ,

а изгибающий момент равен:

- 58 -

M x z ydF

Ey2

dF

E

y2dF

EJ x

,

F

F

F

M

EJ x

.

x

Полученная формула выражает закон Гука при изгибе:

			E		M x E
Поэтому:	z			y
					EJ x

y	M x y		,
	Jx
	z			M x y	.
				J x

1		EJ x	.
		M x

Полученная зависимость называется формулой Навье.

Произведение EJ x называется		изгибной жесткостью и имеет размерность
Н м2 .
Максимальное нормальное напряжение в площади поперечного сечения балки
наблюдается на еѐ поверхности и равно :
				M x	y			M x	.
	z max					max
				J x				Wx

Опасным сечением при изгибе называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение.

§26. Расчеты на прочность при изгибе.

а) проверочный расчет – определяется максимальное расчетное напряжение и сравнивается с допускаемым напряжением:

				M x max		;
	z max
				Wx

б) проектный расчет – подбор сечения бруса производится из условия:

	Wx		M x		max	;
в) определение допускаемой нагрузки – допускаемый изгибающий момент
определяется из условия:	M x Wx .
Далее по полученному значению				M x определяют допускаемые значения
внешних поперечных нагрузок	Q и			внешних изгибающих моментов M в неш .
	y
Условие прочности имеет вид:	Q Q ,			M в неш M в неш .

- 59 -

§27. Касательные напряжения при изгибе. Формула Журавского.

y	P

z	dz
	l

Рассмотрим консольную балку, испытывающую поперечный изгиб. На расстоянии z от заделки выделим элемент длиной dz. Уравновесим его поперечными силами и изгибающими моментами в левой и правой частях.

у

у

у

z

z+d z

b

Mx+dMx

zy

dF

Mx

yz

Qy

у

Qy +dQy

z

z

у1

0

x

dz

dz

zy

N*+d

Продольным

горизонтальным

сечением

на расстоянии у от нейтрального слоя

b

разделим выделенный элемент на две части.

y

z

Рассмотрим равновесие верхней части,

zy

yz

имеющей

основание

шириной

b.

С учетом

закона

парности

касательных

напряжений

x

N*

получаем,

что в поперечном сечении равны

0

в продольном сечении,

направлены друг от

dz

друга по перпендикуляру.

Составим уравнение

Fi z 0 , учитывая, что действию всех

сил должны

противодействовать обратные.

Fi z N N dN yzbdz 0 ,

или

dN yzbdz ,

dN

(1);

yz

bdz

N dF

M x

y dF

M x

y dF

M x

S ,

т.е. N

M x

S

,

J

1

J

1

J

x

J

x

x

x

x

x

F

F

F

тогда:

dN

dM x

Sx

(2).

J x

yz

dM

S

Qy Sx

Подставим (2) в (1):

x

x

.

J xbdz J xb

Полученная зависимость называется формулой Журавского:

Q

S

yz

y

x

,

J xb

где:

Qy

поперечная сила, (Н);

Sx

статический момент отсеченной части сечения,

находящейся выше (или

ниже) некоторой характерной точки, (м3);

Sx F y ,

- 60 -

где:

F

–

площадь части сечения выше (ниже) характерной точки, (м2);

y

–

расстояние от центра тяжести площади

F

до центра тяжести сечения,

(м);

b

–

ширина сечения в некоторой характерной точке,

(м);

J x

–

момент инерции всего сечения относительно центра тяжести (м4).

Определим статический момент прямоугольного сечения со сторонами b и h в

общем случае; для 0 y h

имеем:

2

y

h

h

2

y

F

*

y

b

y

Sx

y

2

2

y

x

h

0

b

h

h

y

h

y

h

y

y

4

2

y

b

2

2

4 2

h

2

hy

hy

y 2

h2

y 2

b

h2

b

b

y 2

8

4

4

2

8

2

2

4

b

Пример.

Определить касательные

напряжения

по высоте прямоугольного (а) и

круглого (б) сечения консольной балки, нагруженной положительной силой Р

на свободном правом торце, построить эпюру касательных напряжений .

y

а)

Обозначим в сечении по его высоте (на оси

1

у)

три характерные точки: 1 –

по верхней

С

h

x

max

образующей; 2 – по нижней образующей; 3

4

3

h

–

в

центре

тяжести

сечения.

Определим

0

2

касательные

напряжения

для

каждой

характерной точки:

b

1

0,

т.к.

S

0 ;

2

0 , т.к.

S 0

;

x

x

Q

y

b h h

3Qy

2

3

2 4

max , т.к. Sx F*

y

b

h

h

bh

Sxmax .

3

bh

b

2bh

2

4

8

12

Площадь эпюры касательных напряжений ограничивается параболой второй

степени. Направление действия напряжений совпадает с направлением действия

поперечной силы.

4R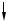

3

1	у			б) По аналогии	с предыдущей задачей,
	С	R		обозначим в	сечении три характерные
3				max
	О		x

Характерными2будем считать точки на оси ординат, располагающиеся по верхней и нижней образующей сечения, в местах изменения его ширины, а также в центре тяжести сечения.