ves_sopromat

- 31 -

Легирующие добавки.

Углерод, марганец, титан, ванадий, ниобий и другие легирующие добавки повышают такие характеристики сталей, как прочность и вязкость.

При высоких температурах в стальных деталях может образовываться окалина на поверхности, поэтому стали добавляют легирующие элементы для повышения прочностных характеристик поверхности, которые также повышают их жаропрочность и жаростойкость.

Жаростойкость – свойство материала противостоять при высоких температурах химическому разрушению поверхности.

Жаропрочность способность материала сохранять механические свойства при высоких температурах.

Концентраторы напряжений.

Концентрация напряжений – это местное повышение напряжений в элементах конструкции, обусловленное резким изменением их геометрии: нал ичие отверстий, выточек, канавок, галтелей и т.п. элементов, называемых

концентраторами напряжений.

Степень концентрации напряжений характеризуется теоретическим коэффициентом концентрации напряжений, определяемым по формуле:

где:

где:

max ,

н

m a x- максимальное напряжение в месте концентрации;

н - номинальное напряжение, определяемое по формуле:

н N ,

Fmin

Fm in - площадь ослабленного (нетто-) сечения.

Форма концентратора напряжений определяет величину теоретического коэффициента концентрации напряжений. Величина теоретического коэффициента концентрации напряжений показывает степень опасности концентратора.

На практике коэффициент концентрации напряжений реальных элементов конструкций оказывается меньше теоретического, он называется эффективным коэффициентом концентрации напряжений и определяется по формуле:

k 1 q( 1) ,

где: q – коэффициент чувствительности материала к концентрации напряжений (зависит от материала и величины ), является справочной величиной.

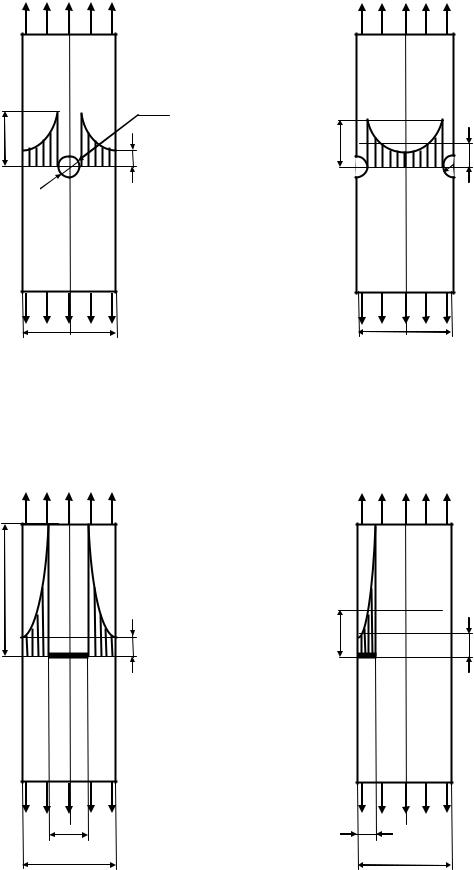
	- 32 -
Полоса металла с круглым	Полоса металла с полукруглыми
отверстием посередине	вырезами по краям

	P			P
	d
max	н	max		r	н
b	P		b	P
d = 0,1b			r = 0,5d		d = 0,1b
= 3			= 2
Полоса металла с короткой		Полоса металла с короткой
поперечной трещиной посередине			краевой трещиной
	P			P
max
		max			н
	н
max =
					b>>l
	P			P
2l			l
b			b
=			=

- 33 -

§12. Виды расчетов на прочность.

Расчет на прочность сводится к требованию, чтобы наиболь шее напряжение в элементе конструкции не превосходили некоторой допускаемой величины.

Методы расчетов на прочность

Метод		Метод		Метод
допускаемых		предельных		разрушающих
напряжений		состояний		нагрузок

Метод допускаемых напряжений.

Основным, наиболее распространенным методом расчета является расчѐт по допускаемым напряжениям. Расчет ведѐтся по величине максимальных напряжений, возникающих в опасной точке нагруженной конструкции. При этом максимальное напряжение сравнивают допускаемым. Допускаемое напряжение определяют исходя из величины коэффициента запаса.

Условие прочности:

max n ,

где: некое предельное напряжение,допускаемое напряжение,

n коэффициент запаса.

Сечение, в котором действует максимальное напряжение, называется опасным сечением. Для него и записывается условие прочности.

При проектном расчѐте задаются значение коэффициента запаса и, исходя из него, определяются «безопасные» размеры детали.

При проверочном расчѐте определяют фактическое значение коэффициента

запаса и сравнивают его с		требуемым		значением. Для пластичных материалов
T , для	хрупких материалов		в . Соответственно		коэффициент	запаса
принимают	по пределу текучести		- nT	или пределу прочности - nв , тогда				для
пластичных материалов Т , для хрупких материалов					в . Величины	n	T	и n
		nТ			nв			в
устанавливаются нормами		проектирования: nT 1,5 2,5 ,			nв 2,5 5,0 .			Для

материалов, неодинаково ведущих себя на растяжение и на сжатие, условие

прочности по допускаемым напряжениям выглядит так:

max р

p ,

max c

c .

Пример.

При центральном растяжении-сжатии условие прочности, в зависимости

от исходных данных, можно записать так:

max

или

max

.

Nmax

N

F

Fmin

max

.

- 34 -

Аналогично расчетам на прочность по нормальным напряжениям, проводятся расчеты на прочность по касательным напряжениям, при этом условие прочности выглядит так:

Метод предельных состояний.

Предельным называется такое состояние конструкции, при котором ее дальнейшая эксплуатация не возможна.

В машиностроении установлены 3 группы предельных состояний:

1 группа – определяется потерей несущей способности – прочности или устойчивости;

	2 группа – определяется	возникновением	чрезмерно	больших
	деформаций или колебаний.

3 группа – определяется образованием и развитием трещин и др.

повреждений.

При проведении расчетов по предельным состояниям учитываются следующие коэффициенты:

1) коэффициент надежности по нагрузке f . Учитывает возможное

увеличение нагрузки по сравнению с ее нормативным значением, приведенным в СНиП (Строительные нормы и правила). При этом расчетная нагрузка определяется по формуле:

Pp Pн f ,

где: Pн - нормативная нагрузка.

f 1,05 1,3 (учет собственного веса, как постоянной нагрузки),

f 1,05 1,4 (учет временной нагрузки – снеговой, ветровой).

2) коэффициент надежности по материалу m . Учитывает возможное уменьшение нормативного сопротивления Rн по сравнению с данными испытаний на образцах.

–для пластичных материалов: Rн Т ;

–для хрупких материалов: Rн В .

Расчетное сопротивление материалов определяется по формуле:

R Rн .

m

Для стали: m =1,025 1,15.

3)коэффициент условий работы с . Зависит от вида конструкции и условий

ееэксплуатации. с 0,75 1,0 .

Проверку по нормальным и касательным напряжениям проводят по фо рмулам:

max	c R ,
или	max c Rc ,

где: Rc 0,6R - расчетное сопротивление материала при сдвиге.

Для стали: R Т .

- 35 -

Метод разрушающих нагрузок.

Для пластичных материалов – разрушающей считается нагрузка, при которой в конструкции возникают значительные пластические деформации и она не способна воспринимать дальнейшее увеличение нагрузки.

Для хрупких материалов – разрушающей считается нагрузка, при которой хотя бы в одном из элементов конструкции возникают напряжения, равные в .

Расчеты на прочность бывают двух видов: проверочный и проектирово чный. Во всех случаях при проведении расчетов на прочность решается одна из трех задач:

проверка выполнения условия прочности (проверка величины макс имальны х напряжений) при заданных размерах конструкции и форме сечений ее элементов, нагрузке и свойствах материалов;

определение размеров сечения заданной формы при известной нагрузке и свойствах материалов;

определение допускаемой нагрузки (грузоподъемности) конструкции при заданных форме и размерах ее элементов и свойствах материалов.

§13. Напряжения в наклонных сечениях при растяжении-сжатии.

					0 против хода
				n1		р	n1
n0				n0	n0		n0
n1
					n1

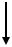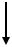N N

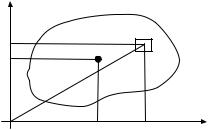
Рассмотрим стержень, нагруженный растягивающей силой N, в наклонном

сечении n1 – n1.

Площадь наклонного сечения n1 – n1 определим по формуле:

F F , Cos

где: F – площадь сечения n1 – n1.

Согласно методу сечений, нормальная сила определяется по формуле:

N pF ,

где: p – напряжения, обусловленные действием силы N.

Тогда: p N NCos Cos . F F

Определим нормальные и касательные

р

внутренняя 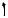С нормаль

напряжения в наклонном сечении n1 – n1 :

pCos Cos Cos Cos2 ,

		pSin Sin Cos	Sin2	,
		2
		т.к. 2Sin Cos Sin2 .

		- 36 -
	Итак, получено: Cos2 ,		Sin2	.
			2

Правила знаков:

1)0, если действует от сечения (при растяжении);

0, если действует к сечению (при сжатии);

2)0, если поворачивается относительно точки С, лежащей на внутренней

нормали, по часовой стрелке;

0, если поворачивается относительно точки С, лежащей на внутренней нормали, против часовой стрелки.

Следствие: max , при = 0 , т.к. Cos0 = 1 ;

max , при = 45 , т.к. Sin90 = 1.

Вывод: максимальные касательные напряжения возникают на площадках, расположенных под углом 45 к нормали поперечного сечения стержня.

Пример: разрушение чугунного образца происходит по площадкам максимальных касательных напряжений.

§14. Геометрические характеристики плоских сечений.

Основные определения.

Введем декартову прямоугольную систему координат XOY. Рассмотрим в плоскости координат произвольное сечение (замкнутую область) площадью F.

y

y		dF			C – центр тяжести сечения;
yc	C				- полярный радиус.
0				x
	xc		x
Статическими моментами сечения относительно осей у и х называются
интегралы вида:
				Sx ydF ;	Sy xdF .
				F	F

Статические моменты сложного сечения можно опр еделить как:

n	n
Sx Sxi ,	S у S уi ,
i 1	i 1

где: i = 1 n – число простых сечений;

- 37 -

Sxi , Syi - статические моменты простых сечений.

Параллельный перенос осей.

При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осей: х1, х2 и у1, у2.

y1

y2

Пусть расстояние между осями х1

и х2

равно b; расстояние между осями у1

и у2

у2

О2

dF

x2

равно a, тогда:

у1

x2 x1 a ;

y2 y1 b .

b

a

х2

x1

Полагаем, что х1, у1

и Sx

, Sy заданы.

1

1

О1

x1

Найдем Sx

и Sy

:

2

2

Sx2

y2dF y1

b dF y1dF bdF Sx1

bF ;

F

F

F

F

Sy2

x2dF x1

a dF x1dF adF Sy1

aF .

F

F

F

F

Итак, получено:

Sx

Sx

bF ,

Sy

Sy aF .

2

1

2

1

Следствие:

если Sx

bF , то

Sx

2

0 ;

1

если Sy

aF , то

Sy

2

0 .

1

Таким образом, всегда можно подобрать расстояния a и b.

Оси, относительно которых статические моменты равны нулю, называются

центральными.

Точка пересечения центральных осей х и у (точка С с координатами хc и yc )

называется центром тяжести сечения.

xc

S y

xdF

yc

S

ydF

F

;

x

F

.

F

F

F

F

Если оси х и у проходят через

центр тяжести сечения, хс = 0 и ус = 0,

следовательно, Sx yc F 0 , S

y

x F 0.

c

Статический момент может принимать положительные, отрицательные и

равные нулю значения и имеет размерность [ l3 ].

Приложение.

y

dF = dxdy

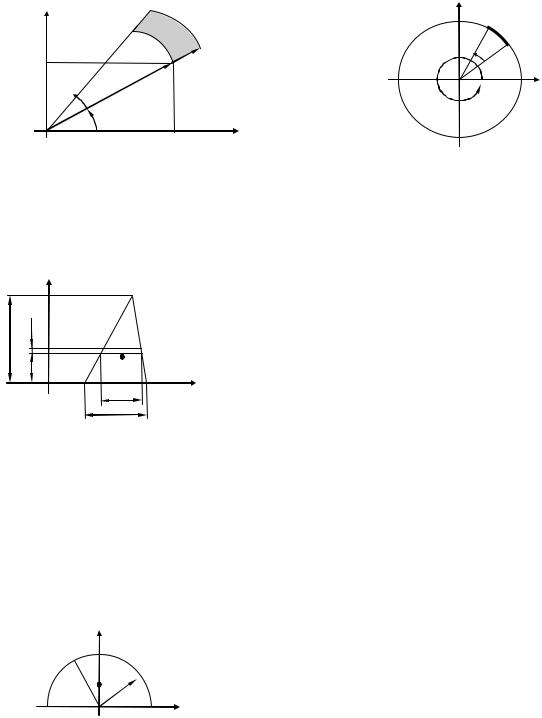
Декартова система координат (х, у).	dy	dF
	y	dх
	0
	x	x

- 38 -

Полярная система координат (r, ).

		dS	у
y	dF			dS
			d
y		dr		R
			dF = rdrd
d	r		О	x
			2
0
	x		x

	Переход к декартовой системе координат:		S 2 R - длина окружности;
	х rCos ,	y rSin .	2		d	, dS Rd .
			2 R		dS

Пример. Определить, на каком расстоянии по высоте от основания находится центр тяжести треугольника произвольной формы.

у

h dу

dF

у

C

О

b(y)

x

b

h

b h y

Sx2

yb y dy y

dy

F

0

h

y

S

x

bh2 2

h

c

F

6 bh

3

Ответ:

y

h

.

c

3

Пример.

у

R

C

r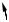

О x

Площадь треугольника

F

1

bh ,

2

dF b y dy .

полагаем, что:

Из подобия двух треугольников следует:

b y

h y

,

b y

b h y

.

b

h

h

h

h

h

2

2

h

3

2

3

2

ybdy

y

b

dy

by

by

bh

bh

bh

0

0

h

2

0

h3

0

2

h3

6

Определить центр тяжести полукруга.

Площадь полукруга	F	R2
		;
		2

R

r

3

R

Cos Cos0

R

3

2

Sx ydF rSin rdrd Sin d r 2dr Cos

R3 .

3

3

3

F

F

0

0

0

0

yc

S

x

2R3 2

0,424 R .

F

3 R2

Ответ: yc

0,424 R .

- 39 -

Осевыми (экваториальными) моментами инерции сечения относительно осей х и у называются интегралы вида:

J x y2dF ;			J y x2dF .
	F		F
Если сечение площадью F можно представить в виде суммы нескольких
замкнутых областей: F F1 F2	Fn , то, по аналогии со статическими моментами:
				n
Sx ydF1 ydF2			ydFn ydFi ;
F1	F2		Fn	i 1 Fi
				n
Sy xdF1 xdF2		xdFn		xdFi ,
F1	F2		Fn	i 1 Fi

осевые моменты инерции можно представить в виде:

			n
Jx y2dF1 y2dF2		y2dFn y2dFi ;
F1	F2	Fn	i 1 Fi
			n
J y x2dF1 x2dF2		x2dFn x2dFi .
F1	F2	Fn	i 1 Fi

Осевые моменты инерции могут принимать положительные и равные нулю значения и имеют размерность [ l4 ].

Полярным моментом инерции сечения относительно начала координат называется интеграл вида:

J x2 y2 dF 2dF ,

	F	F
где: - полярный радиус.
Очевидно,
J x2 y2 dF x2dF y2dF J y J x ,			т.е. J J y Jx .
F	F	F
Полярный момент инерции может принимать положительные или равные нулю
значения и имеет размерность [ l4 ].
Центробежным моментом инерции сечения называется интеграл вида:
		J xу хydF .
		F
Главными осями инерции сечения называются две взаимно перпендикулярные
оси, относительно которых	центробежный момент		инерции Jxу 0 , а осевые

моменты инерции J x и J у принимают экстремальные значения.

Если одна из взаимно перпендикулярных осей является осью симметрии сечения, то Jxу 0 , следовательно, эти оси главные.

Главные оси инерции, проходящие через центр тяжести сечения, называются

главными центральными осями инерции сечения.

Центробежный момент инерции может принимать положительные или равные нулю значения и имеет размерность [ l4 ].

- 40 -

§15. Теорема Штейнера о параллельном переносе осей.

	y1
a	у
= y +
1
у
	О1

y

b

С

х

x1= x + b

dF

x

a

x1

Рассмотрим сечение произвольной формы площадью F. Через его центр тяжести С проведем оси х и у.

Введем новую декартову систему координат X1O1Y1, оси, которой параллельны осям системы XСY.

Обозначим расстояние между осями х и х1 как а; а расстояние между осями у и у1 как b.

По чертежу видно, что: x1 x b , y1 y a ; статические моменты сечения Sx 0 и Sy 0 , т.к. оси х и у проходят через центр тяжести сечения.

Тогда: Sx1 y1dF y а dF ydF аdF Sx аF аF ,

F F F F

Sy1 x1dF x b dF xdF bdF Sy bF bF .

F F F F

J x1 y12dF y a 2 dF y2dF 2aydF a2dF J x 2aSx a2 F J x a2 F ,

F F F F F

J y1 x12dF x b 2 dF x2dF 2bxdF b2dF J y 2bSy b2 F J y b2 F ,

F F F F F

J x1 y1 x1 y1dF x b ) y a dF xydF axdF bydF abdF

F F F F F F

Jxy aSy bSx abF Jxy abF .

Итак, получено: Sx	аF ;	Sy	bF ;
1		1
Jx	Jx a2 F ;		J y	J y b2 F ;	Jx y Jxy abF .
1			1		1	1

§16. Осевые моменты инерции простых сечений.

Пример.
Прямоугольник.
y1						y
	h
2
h						C
									x
	b							b
	2				О		2
	h								x1
						b
2

Рассмотрим прямоугольник с вертикальным ребром h и горизонтальным ребром b. Через его центр тяжести С проведем оси х и у. Введем декартову систему координат, оси которой х1 и у1 параллельны осям х и у, а ее начало лежит в левом нижнем углу прямоугольника.

Определим моменты инерции относительно осей х и у, а также осей х1 и у1 :