Как понимать квантовую механику

13.4. ТЕОРЕМА ГЕЛЛМАНА – ФЕЙНМАНА					373
Усредняя классические уравнения Гамильтона
	dpi	∂H	dqi	∂H	(13.11)
		= − ∂qi ,		= + ∂pi
	dt		dt

по классическому смешанному состоянию (по распределению вероятностей по начальным координатам и импульсам), мы получаем классический аналог теоремы Эренфеста (здесь и далее до конца раздела усреднение уже не квантовое, а классическое):

d pi		= "−	∂H	#,	d qi		= "+	∂H	#.
										(13.12)
dt			∂qi		dt			∂pi

Как и в квантовом случае, в случае общего положения (для нелинейной функции)

F (q, p) =F ( q , p ).

Поведение средних координат и импульсов описывается классическими уравнениями Гамильтона

d pi		∂H	d qi	∂H
	dt	= − ∂qi ( q , p ),	dt	= + ∂pi	( q , p )	(13.13)
для квадратичных гамильтонианов, либо в преде-
ле узкого распределения по координатам и им-
пульсам.
Как в квантовом, так и в классическом слу-
чае мы можем, разлагая правую часть формул
Эренфеста в ряд оценивать поправки к класси-
ческой эволюции средних координат и импульсов,
возникающие за счет¨ неопределенности¨ (конеч-
ной дисперсии) координат и импульсов, а также
моментов (средних отклонений переменных, воз-
веденных¨ в степень) более высоких порядков.					Рис. 13.2. Игорь Василье-
Таким образом, с точки зрения теоремы					вич Волович.
Эренфеста и эволюции средних координат и им-
пульсов, различие между классической				и квантовой теорией		состоит

в некоммутативности квантовых переменных.

13.4. Теорема Геллмана – Фейнмана

Теорема Геллмана – Фейнмана связывает между собой производные по параметру для оператора наблюдаемой и его допустимого значения (собственного числа).

374

ГЛАВА 13

ˆ

Пусть эрмитов оператор A( некоторого числового параметра висеть собственные числа a(λ) и

λ) (например, гамильтониан) зависит от λ. Тогда от этого же параметра будут засобственные векторы |ψ(λ) :

ˆ	ψ(λ)|ψ(λ) = 1.	(13.14)
A(λ)|ψ(λ) = a(λ)|ψ(λ) ,

Отметим, что параметр λ может быть связан с описанием квантовой системы, но не с ее¨ состоянием. Таким параметром может быть масса частицы, постоянная Планка, заряд электрона, какой-либо еще¨ численный коэффициент, но координата, импульс квантовой частицы или любая другая характеристика состояния квантовой системы здесь не годятся. Но, например, координата потенциальной ямы или стенки может быть таким параметром, если они задаются как классические (бесконечно тяжелые)¨ объекты и не могут быть взяты как аргументы волновой функции.

Продифференцируем тождество (13.14) по параметру λ:

∂Aˆ

ˆ

∂|ψ

∂a

∂|ψ

∂λ

|ψ + A

∂λ

=

∂λ

|ψ + a

∂λ

.

Действуя слева бра-вектором ψ(λ)|, получаем:

∂Aˆ

ˆ

∂|ψ

∂a

∂|ψ

ψ|

∂λ

|ψ + ψ|A

∂λ

=

ψ|

∂λ

|ψ + ψ|a

∂λ

.

|

ψ a

(13.15)

(13.16)

Сократив повторяющийся слева и справа член, получаем теорему Геллмана – Фейнмана: при условии (13.14) выполняется тождество

	ˆ			∂a
ψ|	∂A		|ψ =		(13.17)
				∂λ .
	∂λ

Теорема (13.17) полезна при вычислении средних значений от наблюдаемой, которая может быть получена как производная по параметру от другой наблюдаемой, которая определена в рассматриваемом состоянии. При использовании этого метода полезно помнить, что если мы знаем

		ˆ					ˆ
спектр наблюдаемой A, то мы знаем спектр всех наблюдаемых вида F (A),
ˆ2	ˆ3						ˆ
например A	, A	и т. д., и к наблюдаемым вида F (A) можно применить ту
же теорему:			ˆ
					∂F (a)
		ψ|	∂F (A)	|ψ =			(13.18)
						.
			∂λ		∂λ

13.5. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

375

Если рассматриваемые наблюдаемые были определены в классической теории теми же формулами (с точностью до шляпок), то полученное квантовое соотношение между их средними значениями будет совпадать с классическим.

13.5. Квазиклассическое приближение

Исторически квазиклассическое приближение («квазиклассика») предшествовало квантовой механике в ее¨ современном виде. В старых книгах еще¨ можно встретить такие выражения, как старая квантовая механика

и новая квантовая механика.

Первоначально старая квантовая механика «висела в воздухе», представляя собой набор постулатов Бора, которые предписывали правила, согласно которым из множества классических решений уравнений движения каким-то неведомым образом удавалось отбирать те решения, которые соответствовали разрешенным¨ состояниям электронов в атоме.

После создания новой квантовой механики старая квантовая механика была выведена как предельный случай, отвечающий квазиклассическому приближению.

Нам редко удается¨ точно решить уравнения Шредингера,¨ поэтому большое значение имеют методы приближенного¨ решения, к числу которых относится квазиклассика. Важно и то, что квазиклассика позволяет использовать классическую интуицию для квантовых систем. С учетом¨ цели данной книги (понимание квантовой механики) это особенно важно.

13.5.1.Как угадать и запомнить квазиклассическую волновую функцию

Рассмотрим одномерное стационарное уравнение Шредингера¨ в предположении, что на малых расстояниях справедливо приближение де Бройля, т. е. волновую функцию можно записать как

i
ψ(x) ≈ C e ¯h p(x) x	(13.19)

при изменении координаты x на несколько длин волн де Бройля. Это означает, что длина волны, записанная как функция от x, мало меняется на расстоянии порядка длины волны

	∂λ					∂λ
	∂x		|λ|			∂x		1.	(13.20)
		λ

	376			ГЛАВА 13
	Здесь	2π¯h
	λ(x) =		,	p(x) = 2m(E − U (x)).
		p(x)

То есть мы выражаем длину волны через классический импульс частицы. В формуле (13.19) «константа» C зависит от x, поэтому удобнее пере-

писать формулу в другом виде:

ψ(x +

Таким образом, мы получаем

i

p(x0

ψ(x1) ≈ ψ(x0) e ¯h

				i
δx) ≈ ψ(x) e					p(x) δx.				(13.21)
				¯h
	i					i		−δx) δx
) δx e		p(x0	+δx) δx · · · e				p(x1		≈
	¯h					¯h
x1−x0

			δx
		i
≈ ψ(x0) exp				p(x0	+ nδx) δx	≈
		¯h	n=0
			x1
		i
			x0
≈ ψ(x0) exp ¯h			p(x) dx .

Таким образом, произведение px в показателе экспоненты волны

де Бройля в случае медленно меняющегося классического импульса p(x)

заменилось на интеграл p(x) dx:
ψ(x) ≈ C exp	i	p(x) dx .	(13.22)
	¯h

Полученная нами формула (13.22), как мы увидим далее, совпадает с первым квазиклассическим приближением.

Заметим, что волновая функция, описывающаяся формулой (13.22) предполагает, что |ψ(x)|2 = |C|2 = const. Насколько это хорошо?

Если классическая частица движется вдоль оси x, причем¨ E > U (x), то частица будет последовательно проходить все интервалы по x, находясь

	на каждом интервале dx на протяжении времени	dx	= m	dx	, где v(x) —
		v(x)		p(x)

классическая скорость. (То есть в классическом случае отсутствует надбарьерное отражение.) Если мы ловим частицу на интервале dx, не зная

13.5. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

377

в какой именно момент частица стартовала, то вероятность того, что мы поймаем частицу, пропорциональна времени, которое частица пробудет на данном отрезке. Таким образом, следует модифицировать волновую функцию так, чтобы выполнялось условие |ψ(x)|2 p(1x) . Поэтому естественно предположить

ψ(x) ≈		C		exp	±	i	p(x) dx .	(13.23)
		p(x)				¯h

Знак ± в показателе экспоненты соответствует движению частицы по x в положительном или отрицательном направлении. Как мы увидим далее, формула (13.23) совпадает со вторым квазиклассическим приближением.

Поскольку в квантовой механике частица может одновременно двигаться в обе стороны (находиться в суперпозиции состояний, отвечающих движению в разные стороны), последнюю формулу следует модифицировать:

ψ(x) ≈

C+

exp

i

p(x) dx +

p(x)

¯h

+

C−

exp

−

i

p(x) dx . (13.24)

p(x)

¯h

Таким образом, мы угадали формулу для второго квазиклассического приближения, используя общефизические соображения. Далее мы выведем ту же формулу (13.24) более строго, но и метод угадывания, несмотря на всю свою нестрогость может быть полезен, поскольку нестрогий вывод позволяет: 1) понять физический смысл формул; 2) хорошо запомнить сами формулы.

Рассуждения, с помощью которых мы угадали квазиклассические волновые функции применимы только в глубине классически разрешенной¨ области E > U (x), однако можно надеяться, что те же формулы будут справедливы для мнимых значений импульса p(x), т. е. в глубине области E < U (x).

13.5.2. Как вывести квазиклассическую волновую функцию

Выведем в одномерном случае то выражение для квазиклассической волновой функции, которое мы угадали в предыдущем разделе. Для этого представим волновую функцию в экспоненциальном виде

i
ψ(x) = e ¯h S(x)	(13.25)

378

ГЛАВА 13

и подставим ее¨ в стационарное уравнение Шредингера,¨ записанное в координатном представлении:

1		(S )	2		− i¯hS	= E − U (x),		(13.26)
	2m
или
	S =						.	(13.27)
				2m(E − U ) + i¯hS

Это пока точное уравнение Шредингера,¨ просто переписанное для функции S(x).

Мы знаем, что постоянная Планка мала в привычных нам макроскопических единицах измерения. Но на самом деле бессмысленно говорить о малости размерной величины, т. к. любая размерная величина может быть обращена в единицу выбором подходящих единиц измерения. «Малость» постоянной Планка в привычных (макроскопических) единицах измерения

означает, на самом деле, малость по сравнению с привычными (макроскопическими) величинами той же размерности, т. е. по сравнению с характерными значения действия и момента импульса.

Запишем для функции S(x) формальный степенной ряд по степеням постоянной Планка:

S = S0 − i¯hS1 + (−i¯h)2S2 + . . . .

(13.28)

Как правило, этот ряд не сходится, но дает¨ хорошие приближения, если взять от него несколько первых членов.

Подставляя ряд (13.28) в уравнение (13.27) и удерживая соответствующие члены разложения, получаем:

S0(x) = 2m(E − U (x)) = ±p(x) S0(x) = ± p(x) dx.

Здесь p(x) — классическое выражение для импульса через координату x. Аналогично для следующего члена разложения:

(S0 − i¯hS1) = (

+ o(¯h) =

2m(E − U ) + i¯hS0

i¯hp (x)

= p2 + i¯hp

+ o(¯h) = p(x) +

,

2 p(x)

.

p (x)

C

S1

(x) = −

= − ln p(x)

S1(x) = ln

2 p(x)

p(x)

13.5. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

379

Подставляя первые два члена из (13.28) в выражение (13.25) для волновой функции, получаем выражение, которое совпадает с угаданным ранее (13.23):

i 5

ψ(x) = C e± ¯h p(x) dx. p(x)

Чего же мы достигли, получив ранее угаданное выражение? Вопервых, мы его действительно получили, а не угадали, при этом мы можем улучшить наше приближение, взяв следующие члены разложения S(x) по степеням постоянной Планка. Мы можем определить область применимости полученного приближения, оценив следующий член разложения, и уже более обоснованно получить ранее угаданную нами оценку (13.20)

	∂λ
	∂x		1.

Причем,¨ если ранее полученные волновые функции и оценки их применимости были обоснованы для классически разрешенной¨ области E > U (x), p(x) R, а применимость тех же формул для классически запрещенной¨ области E < U (x) мы могли обосновывать, только ссылаясь на аналогию и аналитическое продолжение, то теперь квазиклассическое приближение и критерий его применимости равно обоснованы в глубине классически запрещенных¨ и разрешенных¨ областей.

У границы классически разрешенной¨ и запрещенной¨ областей, когда p(x) → 0 длина волны де Бройля неограниченно возрастает и условие |λ (x)| 1 перестает¨ выполняться. Области E U (x) (p(x) 0) надо исследовать другими способами.

13.5.3. Квазиклассическая волновая функция у точки поворота

В классически разрешенной¨ области квазиклассическая волновая функция представляется суперпозицией двух волн, бегущих слева направо и справа налево (13.24). Если данная энергия относится к невырожденному спектру (непрерывному или дискретному), т. е. если частица не может уйти по координате на одну из бесконечностей, то поток вероятности должен равняться нулю, а амплитуда обеих волн должна совпадать. В этом случае (даже вне зависимости от квазиклассического приближения) волновая функция может быть выбрана вещественной, т. е.

				x
		C		1
ψ(x) =		p(x)	sin	¯h	p(X)dX + ϕ0	.	(13.29)

x0

380				ГЛАВА 13
		2
		1
	–2	0	0	2	4	8
		–1
		–2

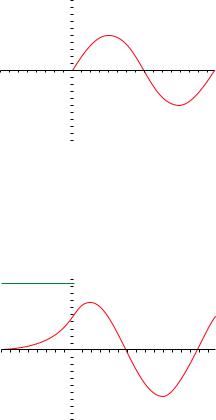
Рис. 13.3. Волновая функция у бесконечновысокой стенки.

В случае, если классически разрешенная¨ область ограничена бесконечновысокой стенкой, в точке a мы имеем ψ(a) = 0 и можем записать

						1	x
ψ(x) =		C										(13.30)
							a
		p(x)			sin ¯h			p(X)dX .
	2
	1
–2	0		0		2			4	8
	–1
	–2

Рис. 13.4. Волновая функция у ступеньки.

Если точка a является точкой поворота (для определенности¨ — левой точкой поворота), где U (a) = E (или U (a −0) > E > U (a + 0)), то и в этом случае удобно выбрать a в качестве предела интегрирования и записать

					1	x
ψ(x) =		C					p(X)dX + ϕ0		(13.31)
						a
		p(x)
				sin ¯h				.

Задача состоит в том, чтобы подобрать фазу ϕ0 так, чтобы формула (13.31) правильно описывала квазиклассическую волновую функцию в глубине классически разрешенной¨ области (вдали от точки поворота a).

13.5. КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

381

Даже если в окрестности точки поворота квазиклассическое приближение не выполняется (например, p(a) = 0), нас, как правило, интересуют не детали поведения волновой функции в малой окрестности точки a, а ее¨ поведение на больших интервалах вдали от этой точки. Для этого достаточно знать фазу ϕ0.

Сравнивая волновые функции в ямах с бесконечновысокими стенками и со стенками конечной высоты, мы можем заключить, что для левой точки поворота ϕ0 > 0 (по крайней мере, для этого случая). То есть если мы хотим заменить стенку конечной высоты, стоящую в точке a, бесконечновысокой стенкой, то стенку придется¨ отодвинуть, чтобы к точке a волновая функция успела набрать фазу ϕ0, т. е. по сравнению с ямой с бесконечновысокой стенкой яма с конечной стенкой «выглядит шире».

В случае, если в окрестности точки поворота (там, где не работает квазиклассика) потенциал можно приблизить линейной функцией, фаза может быть вычислена (см. следующий раздел)

π

ϕ0 = 4 ,

т. е. яма оказывается эффективно шире на 14 полуволны с одной стороны. Если яма с обоих сторон ограничена такими точками поворота, то в общей сложности яма оказывается эффективно шире на 12 полуволны.

Фаза волновой функции у точки поворота*

Введенная¨ выше (13.31) фаза ϕ0 зависит не только от того, как потенциал ведет¨ себя в окрестности точки поворота a, но и от того, как потенциал себя ведет¨ левее: стоит ли где-то при конечном x < a бесконечновысокая стенка, или где-то при x < a есть другая классически разрешенная¨ область, или классически запрещенная¨ область тянется до −∞.

Мы рассмотрим случай, когда вся полуось левее точки a является классически запрещенной¨ областью, причем¨ в окрестности точки поворота, там, где не работает квазиклассика, и немного там, где квазиклассика уже работает, потенциал меняется практически линейно.

Нам надо сшить квазиклассическую волновую функцию слева от точки поворота, которая имеет вид возрастающей вещественной экспоненты (в классически запрещенной¨ области величина p(x) — чисто мнимая)

a

, x a,

C

1

ψ(x) =

−

exp

¯h

p(X) dX

(13.32)

|

p(x)

|

−

| |

2

x

π

ϕ0 = 4 ,

382 ГЛАВА 13

с квазиклассической волновой функцией справа от точки поворота

	C+				1	x
ψ(x) =							p(X)dX + ϕ0		(13.33)
						a
		p(x)		sin ¯h				, x a,

и с точным решением уравнения Шредингера¨ с линейным потенциалом в малой области вокруг точки поворота:

ψ +	2m	F (x	−	a) = 0, F = U (a), x		a.	(13.34)
	¯h2			−

При этом нам надо установить коэффициент пропорциональности между C+ и C− (в силу линейности уравнения Шредингера¨ они должны быть пропорциональны друг другу), а также фазу ϕ0.

Искомый ответ:

C+ = C−.

Эта задача может быть решена различными способами:

•Решение уравнения (13.34) с помощью функции Эйри и сравнение асимптотик функции Эйри при «больших» (но все¨ равно в пределах линейности потенциала) аргументах с квазиклассическими волновыми функциями (13.32) и (13.33) (метод наиболее прямой и обоснованный).

•Продолжение волновой функции на комплексные значения x и получение двух комплексных экспонент (образующих sin в классически разрешенной¨ области) при обходе точки x = a по верхней полуплоскости и по нижней полуплоскости (метод Цваана).

•Вырезание проблемной области x a (замена ее¨ ступенькой, симметричной относительно точки поворота) и сшивка квазиклассических волновых функций (13.32) и (13.33) напрямую позволяет определить правильное значение ϕ0, но не дает¨ правильного отношения амплитуд C±.

	Мы воспользуемся третьим методом.					потенциал линеен) зависит только
	|p(x)| в малой окрестности (где
						¯h
	от |x − a|. При этом |p(a − δ)| = p(a + δ) = p0 δ . Как раз такая си-
	туация изображена на рис. 13.4:
		C−				1
	ψ−(x) ≈				exp	−¯h p0(a − x) ,	(13.35)
		2√
			p0