Как понимать квантовую механику

11.5. СДВИГИ В ФАЗОВОМ ПРОСТРАНСТВЕ**	323
ˆ ˆ
Эрмитовы операторы P и Q не коммутируют (4.64)
ˆ ˆ
[Q, P ] = i¯h,
ˆ	ˆ

соответственно не коммутируют и унитарные операторы Ta и Sb.

Для эрмитовых операторов их некоммутативность удобно определять коммутатором [a, b] = ab − ba = ic (матричным коммутатором) который сопоставляет двум эрмитовым операторам a и b третий эрмитов оператор c.

Произведение и взятие обратного для унитарных операторов — «хорошие» операции, т. к. результат их действия снова оказывается унитарным. Сумма или разность унитарных операторов «хорошими» операциями не являются. Поэтому для унитарных операторов некоммутативность удобнее определять с помощью группового коммутатора ABA−1B−1.

ˆ ˆ

Вычислим групповой коммутатор для операторов Ta и Sb в координатном представлении

ˆ	ˆ ˆ ˆ					ˆ ˆ ˆ
TaSbT−aS−bψ(Q) = TaSbT−a
			i		i
	ˆ	−		bQ		b(Q−a)
			¯h		¯h
	= Ta(e			e		ψ(Q

i

(e ¯h bQψ(Q)) = ˆ −

− a)) = Ta(e

		i
ˆ ˆ			b(Q−a)
		¯h
TaSb(e			ψ(Q − a)) =
i				i
	baψ(Q − a)) = e−				baψ(Q).
¯h				¯h

Таким образом (уже вне зависимости от представления)

ˆ ˆ ˆ ˆ	−	i
		¯h	ab	(11.26)
TaSbT−aS−b = e	.
То есть (читая левую часть равенства справа налево) сдвиги по P , по Q,
обратно по P , обратно по Q дают в итоге фазовый множитель e−				i
					ab, пока-
				¯h

затель экспоненты в котором пропорционален ориентированной (со знаком) площади контура ab, который был описан в фазовой плоскости (Q, P ).

При параллельном переносе (сдвиге) по произвольному контуру, контур может быть приближен с помощью набора прямоугольных ячеек. Внутренние линии этих ячеек проходятся дважды в противоположных направлениях и их вклад сокращается. Таким образом, параллельный перенос в фазовой плоскости (Q, P ) вдоль любого замкнутого контура Γ дает¨ умножение на фазовый множитель

TΓ = e−	i
	¯h S(Γ),	(11.27)

с показателем пропорциональным ориентированной площади контура S(Γ), которая имеется смысл действия по контуру (площадь положительна при обходе контура по часовой стрелке).

324

ГЛАВА 11

С помощью формулы (11.26) можно переставлять сдвиги по координате и импульсу:

	−	i
ˆ ˆ			ab ˆ ˆ	(11.28)
		¯h
TaSb = e			SbTa.

Однако, во многих случаях нам понадобится параллельный перенос одновременно по координате и импульсу вдоль отрезка прямой.

	i	ˆ	ˆ	ˆ
Соответствующий оператор e	¯h	(aP	−bQ)
			вместе с	операторами T−a

ˆ¨

иS−b дает параллельный перенос по контуру в форме прямоугольного треугольника с катетами a и b и ориентированной площадью S = −ab2

	i	ˆ	ˆ		i ab
ˆ ˆ		(aP	−bQ)	= e				(11.29)
	¯h				¯h 2		.
S−bT−ae

Таким образом, оператор сдвига «наискосок» можно выразить через сдвиги по координате и импульсу:

	i	ˆ	ˆ		i	ab	ˆ ˆ
e	¯h	(aP	−bQ)	= e	¯h 2
							TaSb

−	i ab		ˆ ˆ	(11.30)
	¯h 2
= e			SbTa.

11.5.2. Классические и квантовые наблюдаемые**

Оператор сдвига наискосок позволяет, следуя Г. Вейлю, ввести следующую естественную (но не единственную) процедуру, установления соответствия между классическими и квантовыми наблюдаемыми с помощью преобразования Фурье:

F (Q, P ) =		i	(aP −bQ)F˜(b,
	e ¯h
F˜(b, a) =				1
				(2π¯h)2

a) da db,			Fˆ =		i	(aPˆ−bQˆ)F˜(b, a) da db.
				e ¯h
							(11.31)
e−	i	(aP −bQ)F (Q, P ) dQ dP.					(11.32)
	¯h

При этом вещественность классической наблюдаемой F (Q, P ) эквивалента

		ˆ	−	−
равенству F˜(b, a) = F˜ (			b,	a), которое эквивалентно эрмитовости кван-
товой наблюдаемой F .				ˆ
		˜
Чтобы выразить F (b, a) через F нам надо продолжить исследование
оператора сдвига наискосок.
В координатном представлении
	i	ˆ	ˆ		i
e ¯h		(aP −bQ)ψ(Q) = e−			¯h b(Q+a/2)ψ(Q + a).

11.5. СДВИГИ В ФАЗОВОМ ПРОСТРАНСТВЕ**

325

Ядро оператора

			i	ˆ	ˆ	|Q1 = e−			i		+a/2)δ(Q2 − Q1 + a).
Q2|e ¯h				(aP	−bQ)				¯h b(Q2
След оператора сдвига наискосок:
tr e	i				=	Q1|e	i
		(aPˆ−bQˆ)						(aPˆ−bQˆ)|Q1 dQ1 =
	¯h						¯h

i

=e− ¯h b(Q1+a/2)δ(a) dQ1 = 2π¯h δ(b) δ(a),

	i	ˆ	ˆ	ˆ ˆ	ˆ ˆ
tr e	¯h	(aP	−bQ)
				= 2π¯h δ(b) δ(a) = tr(TaSb) = tr(SbTa).

Произведение сдвигов снова дает¨ сдвиг, умноженный на фазовый множитель (направления Q и P на фазовой плоскости ничем не выделены)

i

ˆ

ˆ

i

ˆ

ˆ

i

ˆ

ˆ

· e−

i

e ¯h

(a2P

−b2Q)

· e ¯h

(a1P

−b1Q)

= e ¯h

([a1+a2]P

−[b1+b2]Q)

¯h S ,

Здесь S — площадь треугольника, натянутого на векторы (a1, b1) и (a2, b2):

1

a1

a2

1

S = −

2 b1

b2 = 2 (a2b1 − a1b2).

tr e−

i

(a

Pˆ

b Qˆ)

i

(a

Pˆ

b Qˆ)

= 2π¯h δ(a1 − a2) δ(b1 − b2).

· e ¯h

¯h

2

− 2

1

− 1

ˆ

Теперь мы можем найти коэффициенты разложения оператора F по операторам сдвига наискосок (аналог преобразования Фурье от оператора)

	1		−	i	ˆ	ˆ
˜				¯h	(a2P	−b2Q) ˆ	(11.33)
F (b, a) =	2π¯h	tr	e			F .

Установив с помощью формул (11.31), (11.32), (11.33) взаимно однозначное соответствие между классическими и квантовыми наблюдаемыми мы можем переписать умножение операторов как некоторый частный случай-произведения функций на фазовом пространстве.

326

ГЛАВА 11

11.5.3. Кривизна фазового пространства****

В дифференциальной геометрии пространство считается искривленным,¨ если параллельный перенос по замкнутому контуру дает¨ преобразование отличное от тождественного. Параллельного перенос по замкнутому контуру в фазовой плоскости дает¨ умножение на фазовый множитель (11.27)

i S(Γ)

TΓ = e ¯h , т.е. действие элемента группы U (1). Это означает, что фазовой плоскости можно приписать кривизну над группой U (1). Кривизна фазовой плоскости постоянна, т. к. площадь контура входит в показатель экспоненты с постоянным коэффициентом.

Аналогично кривизна над группой U (1) в пространстве-времени вводится при описании электромагнитного поля как калибровочного.

Можно связать между собой две хорошо разработанных области математической физики: симплектическую геометрию и теорию калибровочных полей. Симплектическая форма и тензор электромагнитного поля объединяют в один объект, задающий кривизну в расслоении фазового пространства над группой U (1). В литературе эта аналогия разрабатывается в одну сто-

рону: квантовая механика как калибровочная теория в фазовом пространстве12.

Пусть XK — координаты в фазовом пространстве. Для коммутаторов и классических скобок Пуассона имеем

ˆ K

ˆ L

] = i¯hJ

KL

,

{X

K

, X

L

} = J

KL

.

[X

, X

В нашей интерпретации JKL — тензор кривизны фазового пространства

над группой U (1).

В канонических координатах

XQi

= Qi, XPj = Pj , JQi Pj = −JPj Qi

= δji , JQiQj

= JPiPj = 0.

Переход от обобщенных¨ импульсов P к кинематическим импульсам p позволяет исключить статическое магнитное поле из гамильтониана, описав его как добавку к кривизне фазового пространства. Для таких («новых канонических») координат x мы обозначим тензор кривизны I (это тот же тензор J, но в других координатах)

xqi = qi = Qi, xpj = pj = Pj − ec Aj (Q), [ˆxK , xˆL] = i¯hIKL, {xK , xL} = IKL,

12Isidro J. M., de Gosson M. A. A gauge theory of quantum mechanics// Mod. Phys. Lett. A. 2007. Vol. 22, Pp. 191–200.

11.5.

СДВИГИ В ФАЗОВОМ ПРОСТРАНСТВЕ**

327

I

qipj

= −I

pj qi

i

,

I

qi qj

= 0,

I

pi pj

e

e

= δj

= c Fij = c (∂iAj − ∂j Ai).

Симплектическая форма ω задается¨ матрицей обратной к матрице I,

т.е. ωKLILM = δKM .

i

e

ωpi pj

= 0.

ωqi pj = −ωpj qi = −δj

,

ωqi qj = c Fij ,

Если не включать в число координат время (как обычно принято в нерелятивистской квантовой механике), то в рамках данного подхода можно описать статическое магнитное поле, компоненты которого задаются компонентами тензора Fij (Fxy = −Hz , прочие компоненты получаем циклическими перестановками индексов).

Данный подход отличается от общепринятого только выбором координат в фазовом пространстве. В качестве примера приведем¨ гамильтониан для системы частиц в магнитном поле в канонических и «новых канонических» координатах:

H =		(Pa − ec A(Qa))2	=		pa2 .
	a	2ma		a	2ma

Здесь a — номер частицы, координаты и импульсы относящиеся к одной частицы объединены в трехмерные¨ векторы. Магнитное поле, в канонических координатах описывается векторным потенциалом A(Qa) (H = rot A), который входит в гамильтониан, а коммутационные соотношения (и тензор кривизны фазового пространства J) не зависят от полей. В «новых канонических» магнитное поле исчезает из гамильтониана и описывается через коммутационные соотношения для компонент кинематических импульсов pa, входя в тензор кривизны фазового пространства I.

Для того, чтобы описать в рамках данного подхода переменное электромагнитное поле, необходимо расширить фазовое пространство, рассматривая время t и соответствующий времени обобщенный¨ импульс p0 = −E как дополнительные координаты. При этом время в квантовой механике не может рассматриваться в полной мере, как координата, волновая функция, по своему физическому смыслу, должна быть квадратично интегрируемой по пространственным координатам, но не по времени, поскольку суммарная вероятность должна сохраняться.

k/m:

ГЛАВА 12

Гармонический осциллятор

Гармонический осциллятор (грузик на пружинке) очень любим в теоретической механике, поскольку гармонический осциллятор — точно решаемая система, во многих случаях хорошо описывающая в первом приближении малые колебания различных систем. Эти достоинства гармонического осциллятора сохраняются и в квантовой механике.

На самом деле, в квантовой механике гармонический осциллятор любят даже больше, чем в классической. Это связано с тем, что гармонический осциллятор приобретает фундаментальное значение при рассмотрении квантованных бозонных полей (в том числе электромагнитного поля), которые без учета¨ взаимодействия описываются набором невзаимодействующих квантовых гармонических осцилляторов (см. ниже раздел 12.11).

Решать задачу о квантовом гармоническом осцилляторе можно разными способами. Метод лестничных операторов, который вводится здесь, не является универсальным способом решения задач квантовой механики: он хорош только для гармонического осциллятора и похожих на него систем, однако именно этот способ задает¨ специальный язык, который интенсивно используется во многих разделах квантовой теории, включая квантовую теорию поля (КТП).

Знакомство с данным методом очень полезно для изучающих квантовую теорию. Помимо того, что этот способ просто красив, он приучает, столкнувшись с задачей, хорошенько подумать, прежде чем писать уравнение Шредингера¨ в форме дифференциального уравнения (хотя бы потому, что дифференциальные уравнения могут вообще не понадобиться).

Как обычно, начнем¨ решение задачи с выписывания соответствующего

гамильтониана. Удобно записывать уравнения не через жесткость¨ пружи-

ны k, а через собственную циклическую частоту ω =

ˆ	pˆ2		kxˆ2		pˆ2		mω2xˆ2
H =		+		=		+		.	(12.1)
	2m		2		2m		2

12.1. ОБЕЗРАЗМЕРИВАНИЕ

329

12.1. Обезразмеривание

Для упрощения выкладок полезно обезразмерить гамильтониан, представив его в виде: (число с размерностью энергии) × (безразмерный оператор). «Число с размерностью энергии» удобно взять не случайным образом, а естественным, т. е. скомбинировать константу с размерностью энергии из параметров задачи. Из унаследованных от классического осциллятора параметров m и ω составить константу с размерностью энергии («естественную единицу энергии») для гармонического осциллятора невозможно, однако в квантовой задаче у нас появляется еще¨ один масштаб — постоянная Планка ¯h, имеющая размерность действия. Эта размерность может быть представлена как (действие) = (масса) × (длина)2/(время) = = (энергия) × (время) = (импульс) × (длина). Произведение ¯hω имеет как раз размерность энергии, вынося его за скобку, получаем

	pˆ2
ˆ			mωxˆ2		(12.2)
H = ¯hω	2¯hωm	+	2¯h	.

От постоянных множителей в скобках мы можем избавиться, выбрав подходящие единицы измерения координаты и импульса. Поскольку выражение

ˆ ˆ

в скобках безразмерно, новые координата Q и импульс P оказываются безразмерными:

ˆ2

ˆ

2

ˆ

P

(12.3)

H = ¯hω

2

+

2

,

pˆ

pˆ

xˆ

Pˆ =

=

Qˆ = xˆ

4

mω

=

(12.4)

,

¯h

,

√

p0

x0

¯hωm

4

¯h

p0 = √¯hωm,

x0 =

p0x0 = ¯h

(12.5)

,

mω

— осцилляторные единицы импульса, координаты и действия (последняя, естественно, совпадает с постоянной Планка ¯h). До сих пор все наши выкладки можно было один к одному повторить для классического осциллятора, стерев шляпки над буквами и считая ¯h просто некоторой константой с размерностью действия.

Поскольку коммутатор координаты и импульса [ˆx, pˆ] = i¯h имеет в квантовой механике фундаментальное значение, перепишем его в обезразмеренных операторах (числовые множители можно выносить из-под

330

ГЛАВА 12

коммутатора):

pˆ

1

[ˆx, pˆ]

mω

mω

[Q,ˆ Pˆ] = $xˆ

4

¯h

,

%

=

4 ¯h

[ˆx, pˆ] =

= i.

√

√

¯h

¯hωm

¯hωm

ˆ

ˆ

(12.6)

[Q, P ] = i.

В классической механике роль, аналогичную коммутатору, играет скобка Пуассона, и в точности те же выкладки можно проделать для нее,¨ используя соответствие [·, ·]/(i¯h) −→ {·, ·}.

12.2. Представление чисел заполнения

12.2.1. Лестничные операторы

Впеременных Q, P эволюция классического осциллятора сводится

квращению точки на фазовой плоскости вокруг начала координат с постоянной угловой скоростью ω.

Рис. 12.1. Эволюция классического осциллятора сводится к вращению точки на фазовой плоскости (Q, P ).

Вращение с постоянной угловой скоростью удобно описывается с помощь комплексной переменной z = const · (Q + iP ). Вращение задается¨ умножением на фазовый множитель: z(t) = e−iωt z(0).

12.2. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ

331

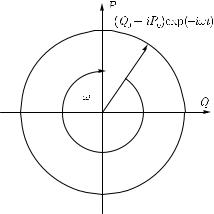
Поскольку в квантовой механике комплексные числа и фазовые множители вида e−iωt являются неотъемлемой частью математического аппарата, представляется естественным попробовать ввести аналогичные величины для описания квантового осциллятора:

	ˆ ˆ					ˆ ˆ
aˆ =	Q + iP			,	aˆ† =	Q − iP			.	(12.7)
	√					√
		2					2

ˆ ˆ †

В отличие от Q и P операторы aˆ и aˆ не являются эрмитовыми. Вычислим коммутатор введенных¨ операторов (коммутатор можно рас-

сматривать как разновидность умножения, и раскрывать скобки обычным образом, с уч¨етом порядка сомножителей, т. е. операция взятия коммутатора дистрибутивна относительно сложения):

[ˆa, aˆ†] = $

ˆ ˆ

ˆ

ˆ

1

Q + iP

,

Q

iP

Qˆ] − i[Q,ˆ Pˆ] + i[Pˆ, Qˆ] + [Pˆ, Pˆ] =

√2

√−2 % =

2 [Q,ˆ

1

=

(0 − i · i + i(−i) + 0) = 1.

2

aˆaˆ† = aˆ†aˆ + 1.

(12.8)

[ˆa, aˆ†] = 1

Если бы операторы aˆ и aˆ† коммутировали, то в соответствии с форму-

лой1 (A − B)(A + B) = A2 − B2

их произведение дало бы обезразмерен-

ˆ

1

ˆ2

ˆ2

H

ный гамильтониан

=

2 (Q + P

). Однако с учетом¨ некоммутативности

ω¯h

операторов получаем:

ˆ

ˆ ˆ

ˆ

1

Qˆ · Qˆ + iQˆ · Pˆ − iPˆ · Qˆ + Pˆ · Pˆ =

aˆ†aˆ =

Q

√−

iP Q + iP

= 2

√

2

2

1

2

+ i[Q,ˆ

Pˆ] + Pˆ

2

.

= 2

Qˆ

ˆ

Введем¨ теперь оператор N :

Nˆ = aˆ†aˆ =

1

2

− 1 + Pˆ

2

2

Qˆ

,

(12.9)

через который и выразим гамильтониан:

Hˆ = ¯hω

1

Nˆ

1

aˆ†aˆ + 2 = ¯hω

+ 2 .

(12.10)

1Эта формула справедлива тогда и только тогда, когда

[A, B] = AB − BA = 0

, поскольку

(A − B)(A + B) = A

2

− B

2

+ AB − BA = A

2

− B

2

+ [A, B].

332 ГЛАВА 12

Задача исследования гамильтониана свелась к задаче исследования эрмито-

2 ˆ †

вого оператора числа квантов N = aˆ aˆ.

Мы видим, что в данных выражениях отличие квантовых формул от классических состоит в появлении константы 12 . В классическом пределе,

ˆ ˆ

когда операторы Q и P могут быть заменены большими (по сравнению с единицей) числами, этой добавкой можно пренебречь.

Операторы aˆ и aˆ† называют лестничными операторами. Смысл этого термина мы сейчас раскроем, для этого вычислим их коммутаторы с опера-

ˆ	ˆ ˆ ˆ ˆ ˆ	ˆ ˆ ˆ ˆ
тором N (воспользовавшись формулой [AB, C] = A[B, C] + [A, C]B и фор-
мулой [A, B]† = [B†, A†]):
	[Nˆ , aˆ] = [ˆa†a,ˆ aˆ] = aˆ†[ˆa, aˆ] + [ˆa†, aˆ]ˆa =	a,ˆ
		−

ˆ † † ˆ − †

[N , aˆ] = [ˆa , N ] = aˆ .

Таким образом мы можем записать коммутационные соотношения в единообразном виде:

[Nˆ , aˆ±] = ±aˆ±,	aˆ+ = aˆ†,	aˆ− = aˆ.	(12.11)
		ˆ
Пусть |ψn — некоторое собственное состояние оператора N :
ˆ			(12.12)
N |ψn = n|ψn .

Исследуем как ведет¨ себя состояние |ψn под действием операторов aˆ и aˆ†,

| †| ˆ

подействовав на получившиеся состояния aˆ ψn и aˆ ψn оператором N :

ˆ	ˆ ˆ	ˆ
N aˆ|ψn = (ˆaN + [N , aˆ])|ψn = (ˆaN − aˆ)|ψn =
	ˆ
	= aˆ(N − 1)|ψn = aˆ(n − 1)|ψn ,
Nˆ aˆ†|ψn = (ˆa†Nˆ + [Nˆ , aˆ†])|ψn = (ˆa†Nˆ + aˆ†)|ψn =
	= aˆ†(Nˆ + 1)|ψn = aˆ†(n + 1)|ψn ,
	Nˆ (ˆa±|ψn ) = (n ± 1)(ˆa±|ψn ).		(12.13)

Формула (12.13) означает, что для произвольного состояния |ψn , удовлетворяющего условию (12.12), состояния a±|ψn либо являются собственными, с собственными числами n ± 1, либо являются нулевыми векторами. Поэтому оператор a+ = a† называется повышающим оператором, а a− = = a — понижающим оператором.

2 ˆ ˆ † † † † †† † ˆ

Эрмитовость оператора N легко проверяется: N = (ˆa aˆ) = aˆ aˆ = aˆ aˆ = N .