Как понимать квантовую механику

12.2. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ				333
ˆ
Оператор N имеет только неотрицательные средние:
ψ|Nˆ |ψ = ψ|aˆ†aˆ|ψ = aψˆ |aψˆ 0.				(12.14)
Для собственного состояния имеем
ˆ	n |ψn = n ψn|ψn 0		n 0.	(12.15)
ψn|N |ψn = ψn|
	число
Возьмем¨ теперь

произвольное собственное состояние и начнем¨ на него много раз действовать понижающим оператором:

aˆ|ψn , aˆ2|ψn , · · · , aˆk|ψn , · · · .

ˆ

Каждый раз оператор aˆ либо понижает собственное число оператора N на единицу, либо обнуляет состояние. Поскольку, как мы показали только что,

ˆ

собственные числа оператора N неотрицательны, рано или поздно очередное состояние

|ψn0 = const · aˆk|ψn

(12.16)

обнулится под действием aˆ:

| † | ˆ | |

aˆ ψn0 = 0 aˆ aˆ ψn0 = N ψn0 = n0 ψn0 = 0 n0 = 0.

ˆ

Мы видим, что это состояние — собственное для оператора N собственным числом:

aˆ|ψ0 = 0.

с нулевым

(12.17)

Оно отвечает минимальной возможной энергии гармонического осциллятора E0 = ¯hω2 , а потому называется основным состоянием гармонического осциллятора.

Легко видеть, что ненулевое состояние |ψ никогда не обнулится под

действием повышающего оператора aˆ†:
aˆ†ψ|aˆ†ψ = ψ|aˆaˆ†|ψ = ψ|Nˆ + 1|ψ ψ|ψ > 0.	(12.18)

Таким образом, начиная с основного состояния |ψ0 и действуя на него раз за разом повышающим оператором aˆ†, мы получаем лестницу состояний, нумеруемых целыми неотрицательными числами. Однако надо уточнить следующие вопросы:

•Сколько может быть линейно независимых состояний |ψ0i , удовлетворяющих уравнению (12.17)? Сколько угодно. До сих пор мы не вводили никаких условий, которые как бы то ни было ограничивали это число. Мы еще¨ вернемся¨ к этому вопросу.

334	ГЛАВА 12
•	ˆ
	Все ли собственные состояния оператора N будут получены из |ψ0i
	с помощью повышающего оператора aˆ†? Все (см. объяснения ниже).
	ˆ
	– Могут ли быть у оператора N нецелые собственные числа? Нет.

Пусть |ψn — собственное состояние, отвечающее произвольному числу n, начнем¨ действовать на него раз за разом понижающим

оператором. Рано или поздно (как мы уже упоминали) мы получим (12.16), что aˆk|ψn = ,0но aˆk+1|ψn = 0, это означает, что

состояние aˆ	k	ˆ
		|ψn — собственное для оператора N , с собственным

числом 0 = n − k, т. е. n = k — целое неотрицательное число.

ˆ

– Могут ли быть у оператора N собственные состояния, которые не получаются из |ψ0i с помощью повышающего оператора?

Нет. Начнем¨	ˆ
	строить собственные состояния оператора N в виде

|ψni = cn (ˆa†)n|ψ0i . Предположим, что |φn — собственное состояние, линейно независимое от |ψni и отвечающее собственному числу n . При этом n > 0, т. к. иначе |φn — просто еще¨ одно состояние из набора {|ψ0i }i. Выберем минимальное значение n .

|

1

оператором aˆ, получаем собственное сос-

Подействовав на

φn

тояние |φn −1 =

· aˆ|φn (где aˆ|φn = ,0т. к. n > 0). Мы

n

видим, что aˆ†

φ

=

1

aˆ†aˆ φ

=

1

Nˆ

φ

= φ

. То

n −1

n ·

n ·

n

n

|

| n

|

|

есть состояние |φn получается из состояния |φn −1 с помощью

оператора aˆ†. Если |φn −1 линейно независимо от |ψ(n −1)i , то выбранное нами n не минимально, а если зависимо, то |φn

представимо через |ψn i .

• Сколько может быть линейно независимых состояний |ψni , отвечаю-

ˆ

щих произвольному собственному числу n оператора N ? (То есть как зависит от n кратность вырождения?) Ровно столько же, сколько для n = 0 (см. первый вопрос), т. е. для всех n непременно поровну. Пусть n > 0. Состояния aˆ|ψni ненулевые (т. к. n > 0) и линейно

независимые (т. к. если они линейно зависимы, т. е.							i ciaˆ|ψni = 0,
то	0 = aˆ†0 = aˆ†	i	c aˆ ψ	=	i ciaˆ†aˆ|ψni = i	c n ψ		, т. е. ли-
			i | ni			i	| ni

нейно зависимы исходные состояния). Следовательно, кратность вы-

рождения не может увеличиваться с ростом n. Аналогично для любого целого неотрицательного n состояния aˆ†|ψni ненулевые и линейно независимые (т. к. если они линейно зависимы, т. е. i ciaˆ†|ψni = 0,

то	0 = aˆ0 = aˆ i ciaˆ†|ψni =	i	c	aˆaˆ	†|	ψ	=	(n	+ 1)|ψni	, т. е.
			i			ni		i ci

линейно зависимы исходные состояния). Следовательно, кратность вы-

рождения не может уменьшаться с ростом n.

12.2. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ЗАПОЛНЕНИЯ

335

12.2.2. Базис собственных функций

Пусть кратность вырождения равна единице, тогда собственные функ-

ˆ

ции оператора N нумеруются одним числом n. Эти собственные функции, будучи собственными функциями эрмитова оператора, образуют базис, для элементов которого удобно ввести следующие обозначения:

|ψn = |n .

(12.19)

Базис является ортогональным, т. к. собственные векторы, отвечающие разным собственным числам, ортогональны. Базисные векторы отнормируем на единицу (поскольку спектр дискретный, это возможно), таким образом

k|n = δkn.

(12.20)

Под действием понижающего оператора базисные векторы ведут себя следующим образом:

aˆ|0 = 0,	(12.21)
aˆ|n = cn|n − 1 , cn C,	n > 0.

Что мы можем сказать о константах cn? Сопрягая последнее уравнение и умножая исходное уравнение слева на сопряженное,¨ получаем:

n|aˆ† = n − 1|cn,

n|aˆ†aˆ|n = n − 1|cncn|n − 1 ,

n|aˆ†aˆ|n = n|Nˆ |n = n|n|n = n n|n = n,

n

−

1 c c

n

1

= c c

n

n

−

1 n

1

= c c

n

= c

2.

| n

n| −

n

| −

n

|

n|

|cn|2 = n

cn = eiϕn √

n.

Таким образом, используя ортонормированность базиса, мы вычислили cn с точностью до фазовых множителей. Вычислить эти фазовые множители невозможно. Это связано с тем, что условие ортонормируемости зафиксировало наш базис только с точностью до умножения базисных векторов на произвольные различные фазовые множители:

|n = eiφn |n ,

cn = ei(φn−φn−1)cn.

Не имея возможности вычислить фазовые множители для cn, мы имеем возможность выбрать их по своему произволу. Мы выберем все cn вещественными неотрицательными числами. Это зафиксирует большую часть

336 ГЛАВА 12

произвола, теперь мы можем умножать наши векторы только на одинаковые
фазовые множители (|n = eiφ0 |n , а cn = √n теперь — фиксированные
числа):	√	(12.22)
	aˆ|n = n |n − 1 .

Запишем матричные элементы оператора aˆ для базисных векторов. Матричные элементы оператора aˆ† получаются эрмитовым сопряжением:

√ √ √

k|aˆ|n = n δk,n−1 n|aˆ†|k = n δk,n−1 = k + 1 δk+1,n.

(12.23)

Это позволяет представить лестничные операторы в виде матриц

		0 1	0		0 . . .
		0 0	√		0 . . .
				2
					√3 ... .
aˆ =		0 0	0						, aˆ†
		0 0	0		0 ..
					. .
	. . .							..
	.. .. ..				..

		0	0		0		0 . . .
		1	0		0		0 . . .
=		0	√2		0		0 . . .				.	(12.24)
		0	0		√3		0 . . .
					.		.		.
	. .							..		..
	.. ..				..

Столбцы и строки нумеруются здесь целыми числами, начиная с нуля. Таким образом, мы получили действие aˆ† на базисные векторы

√	(12.25)
aˆ†|n = n + 1 |n + 1 .

На основе (12.25) мы можем выразить состояние |n через основное состояние |0 :

(ˆa†)n	(12.26)
|n = √ |0 .

n!

Обратите внимание, формулы (12.22) и (12.25) мы получали поразному. Это связано с тем, что вывод формулы (12.22) предполагал произвольную фиксацию фазовых множителей. Выводя формулу (12.25), мы уже не могли фиксировать фазовые множители произвольно, а должны были воспользоваться соглашениями, принятыми ранее, поэтому формула (12.25) была выведена через формулу (12.22).

ˆ

Мы нашли собственные числа оператора N , используя (12.10) мы можем записать разрешенные¨ уровни энергии гармонического осциллятора:

En = ¯hω n +	1	, n = 0, 1, 2, 3, . . . .	(12.27)
	2

12.3. ПЕРЕХОД К КООРДИНАТНОМУ ПРЕДСТАВЛЕНИЮ

337

Целое число n можно трактовать как число фиксированных квантов энергии ¯hω, сообщенных¨ осциллятору сверх энергии нулевых колебаний 12 ¯hω. По этой причине n называют числом заполнения, а разложение волновой функции по базису {|n }∞n=0 — представлением чисел заполнения.

12.3. Переход к координатному представлению

До сих пор мы не установили кратность вырождения уровней для гармонического осциллятора. Кроме того, выбрав стационарные состояния в качестве базисных, мы ничего не сказали про их вид в координатном представлении. Впрочем, можно просто постулировать нужную кратность вырождения, а все вычисления проводить в представлении чисел заполнения.

В координатном представлении

xˆ = x,

pˆ = −i¯h

∂

ψ(x) = x|ψ .

,

∂x

Переходя к обезразмеренным операторам получаем:

Qˆ = Q, Pˆ = i¯h

∂

1

= i

∂

, ψ(Q) =

Q ψ

= √

ψ(x)

|x=Q·x0

.

x

∂(Qx0) p0

−

−

∂Q

|

0

√ (12.28)

Корень x0 возникает как нормировочный множитель, чтобы обеспечить нормировку на единицу для волновой функции, как функции Q:

|ψ(Q)|2dQ = |ψ(x = Q · x0)|2 d(x0Q) = |ψ(x)|2dx = 1.

В координатном представлении лестничные операторы принимают вид дифференциальных операторов:

Q +

∂

Q −

∂

∂Q

∂Q

aˆ =

,

aˆ† =

.

(12.29)

√

√

2

2

Если теперь записать уравнение (12.21), то оно превратится в дифференциальное уравнение

	Q +		∂
aˆ|0 = 0			∂Q
						ψ0(Q) = 0.	(12.30)
	√
		2

338

ГЛАВА 12

Мы получили обыкновенное (поскольку у нас одна независимая переменная Q, «круглые» дифференциалы можно заменить на «прямые»), линейное, однородное дифференциальное уравнение первого порядка, а значит, решение этого уравнения единственно с точностью до постоянного множителя (нормировочной константы). Это уравнение с разделяющимися переменными, так что оно без труда решается явно:

Qψ0 +			dψ0	= 0
			dQ
	dψ0							Q2										e−	Q2
		= Q dQ				ln ψ =					+ const			ψ		= const			2 .
	ψ0						−		2								·
			−			0									0
							0.7
							0.6
							0.5
							0.4
							0.3
							0.2
							0.1
							0
					–4	–2			0		2		4

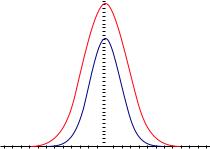
Рис. 12.2. Основное состояние гармонического осциллятора и его квадрат: ψ0(Q) и |ψ0(Q)|2. Две вертикальные черты обозначают границы классически разрешенной¨ области.

С точностью до фазы множитель определяется из условия нормировки. Если выбрать фазу так, чтобы функция ψ0(Q) была вещественной и положительной, то

	1			−	Q2
ψ0(Q) =			· e		2	.	(12.31)
	√4
		π

Основное состояние единственно, с точностью до множителя, т. е. кратность вырождения — единица.

Мы можем получить и другие кратности вырождения, если добавим волновой функции дополнительные аргументы, например, рассмотрим

12.3. ПЕРЕХОД К КООРДИНАТНОМУ ПРЕДСТАВЛЕНИЮ

339

0.6

0.4

0.2

		0
–4	–2	0	2	4

–0.2 Q

–0.4

–0.6

Рис. 12.3. Первое возбужденное¨ состояние гармонического осциллятора: ψ1(Q) и |ψ1(Q)|2.

осциллятор с волновыми функциями вида ψ(Q, m), где Q — непрерывная координата, а m — дискретная переменная, пробегающая K значений (например, проекция спина, тогда K = 2s + 1), даст K-кратно вырожденный спектр. (Собственные функции, отвечающие одинаковой энергии, будут нумероваться еще¨ и значением переменной m.)

	0.6
	0.4
	0.2
	0	0
–4	–2		2	4
	–0.2	Q
	–0.4

Рис. 12.4. Второе возбужденное¨ состояние гармонического осциллятора: ψ2(Q) и |ψ2(Q)|2.

Возбужденные¨ состояния получаются из основного состояния (12.31) с помощью повышающего оператора aˆ† по формуле (12.26). Но теперь по-

340 ГЛАВА 12

вышающий оператор оказывается дифференциальным оператором, в соответствии с формулой (12.29):

(ˆa†)n

ψn(Q) =

ψ0(Q) =

√

n!

Q −

∂

n

Q2

1

∂Q

1

=

√n!

√2

√4 π

· e− 2 =

∂

n Q2

n

1/2

e− 2 .

= (√π2

n!)−

Q

−

∂Q

Q2

Q2

Поскольку

∂

e−

= −Q e−

, из предыдущей формулы легко ви-

2

2

∂Q

деть, что волновая функция n-го возбужденного¨ состояния имеет вид

√

−

Q2

n

n!)−

1/2

2

,

ψn(Q) = ( π2

Hn(Q) e

где Hn(Q) — полином степени n, который называется полиномом Чебыш¨ева – Эрмита.

Обратите внимание, что как дифференцирование по Q, так и умножение на Q меняют четность¨ волновой функции, таким образом, под действием операторов aˆ и aˆ† четные¨ волновые функции превращаются в нечетные¨ и наоборот. Поскольку ψ0(Q) — четная¨ функция, четности¨ ψn(Q) и полинома Эрмита Hn(Q) соответствуют четности¨ n.

Приведем¨ первые 6 полиномов Эрмита:
H0 = 1, H1 = 2Q, H2 = 4Q2 − 2,					H3 = 8Q3 − 12Q,
H4 = 16Q4 − 48Q2 + 12,		H5 = 32Q5 − 160Q3 + 120Q.
Мы можем записать формулу для n-го полинома в виде
	Q2			n	Q2
			∂
Hn(Q) = e 2		Q −		e− 2 .
			∂Q

Данную формулу легко упростить, вставив перед скобками выражение

Q2	e−	Q2	и «пронеся» e−	Q2
e 2		2		2 направо через все производные с помощью

12.3. ПЕРЕХОД К КООРДИНАТНОМУ ПРЕДСТАВЛЕНИЮ

341

0.6

0.4

0.2

		0
–4	–2	0	2	4

–0.2 Q

–0.4

–0.6

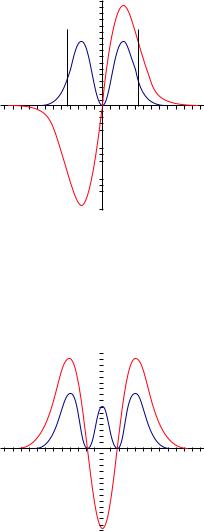
Рис. 12.5. Третье возбужденное¨ состояние: ψ3(Q) и |ψ3(Q)|2.

очевидной формулы:

		Q2		∂			∂		Q2
	e− 2		Q −		F (Q) =	−		e− 2 F (Q).
				∂Q			∂Q

В результате получаем стандартную «формулу из учебника»:

		Q2		∂		n	Q2
			−			e−
	Hn(Q) = e			∂Q			.
		0.4
		0.2
–10	–5	0 0					5	10
		–0.2	Q
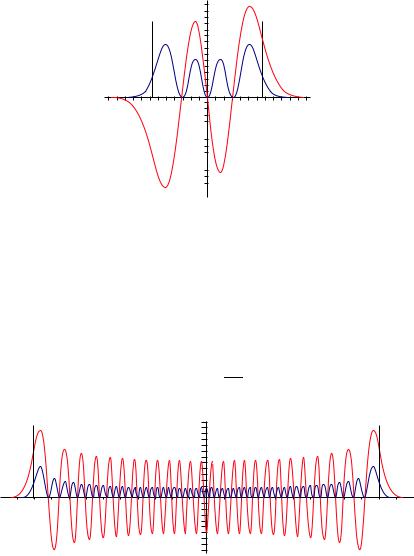
Рис. 12.6. 50-е возбужденное¨ состояние				гармонического				осциллятора: ψ50(Q)
и |ψ50(Q)|2.

342

ГЛАВА 12

12.4.Пример расчетов¨ в представлении чисел заполнения*

Пусть, например, нам надо посчитать среднее от какого-либо операто-

ˆ ˆ2	ˆ
ра, скажем, QP	Q в состоянии |n . Можно, конечно, найти волновую функ-
	ˆ ˆ2		ˆ		2	Qψn dQ, од-
цию ψn(Q) и взять интеграл n|QP			Q|n =		ψnQ(−i∂/∂Q)
нако проще провести вычисления в		представлении чисел заполнения.
				5

Мы знаем, как на собственные функции осциллятора действуют лестничные операторы, поэтому выразим через них операторы координаты

и импульса:

Qˆ =

aˆ + aˆ†

,

Pˆ =

aˆ − aˆ†

.

(12.32)

√

√

2

i

2

Теперь мы можем написать

n|QPˆ ˆ2Qˆ|n = n|aˆ √2

†

i−√2 †

2

√2

†

|n =

+ aˆ

aˆ aˆ

aˆ + aˆ

Далее остается¨ раскрыть скобки (не забывая, что aˆ и aˆ† не коммутируют!), применить формулы для действия лестничных операторов на базисные состояния (12.22), (12.25) и ортонормированность базисных состояний (12.20).

Впрочем, мы можем облегчить работу, выписывая при открытии скобок только те члены, которые содержат равное число операторов aˆ и aˆ†, поскольку каждый такой оператор опускает (поднимает) состояние на одну ступеньку, а состояния ортонормированы, а значит нам интересны только члены, не меняющие номер состояния. Таким образом, продолжаем предыдущее равенство

=

1

n

aˆ†aˆ†aˆaˆ

−

aˆ†aˆ aˆ†aˆ + aˆ†aˆ aˆaˆ† +

−

4

| −

ˆ

ˆ

ˆ

ˆ

+ aˆaˆ†

†

aˆaˆ†

†

† †

−

N

N

N

(N +1)

aˆ aˆ

aˆaˆ

−

|

=

ˆ

ˆ

ˆ

ˆ

(N+1)

N

(N +1) (N +1)

Мы просто выписали все 6 возможных способов поставить два креста на 4 оператора. При этом каждый крест над вторым или третьим оператором

ˆ

(которые происходят от оператора P ) давали знак минус.

Мы сразу выделили действующие на состояние |n комбинации опера-

ˆ

торов, которые дают оператор номера уровня N . Поскольку оператор действует на свое¨ собственное состояние, его можно заменить собственным