
487_Algebra_11
.pdfБоймурод Алиев
АЛГЕБРА
Китоби дарсї барои синфи 11
Њайати мушовараи Вазорати маорифи Љумњурии Тољикистон ба чоп тавсия кардааст
Душанбе – 2006
1
МУЌАДДИМА
Мо омўзиши предмети «Алгебра ва ибтидои анализ»-ро, ки дар синфи 10 сар карда будем давом медињем. Мундариљаи китоб аз доираи барномаи таълимї васеътар буда, ќариб тамоми маводи таълимии мактабњои тамоили риёзиро дар бар мегирад. Сохтори китоб бо сохторњои китобњои дарсии синфњои 7-10, ки дар чанд соли охир чоп шудаанд, як хела аст.
Китоб аз се боб иборат аст. Дар боби 1 мафњумњои нав - функсияи ибтидої ва интеграл, баъзе хосиятњо ва татбиќоти онњо омўхта мешавад. (Бояд гуфт, ки анализ ба курси математикаи олї мансуб аст. Дар мактаби миёна танњо элементњои он омўхта мешавад.) Боби 2 аз омўзиши мафњуми функсияи нишондињан-дагї ва хосиятњои он сар мешавад. Баъд мафњуми нав – логарифм, ки амали баръакси бадараљабардорї аст, оварда мешавад. Хосиятњои логарифм, тарзњои њал кардани муодилањои нишондињандагї ва логарифмї ќисми асосии ин боб мебошанд. Боб бо мафњум дар бораи муодилањои дифферент-сиалї ба итмом мерасад.
Њалли мисолу масъалањои овардашудаи ин ду боб зарурияти истифодаи тамоми пањлўњои маводи назарявиро талаб мекунад. Барои њамин дар аввал ќисми назарявии пунктро бо диќќат омўхта, ба саволњои назоратї љавоб гардонида, мисолњои дар он њалшударо аз худ кунед. Баъд ба њалли супоришњо шурўъ намоед. Дар пунктњо супоришњо тавре љойгир карда шудаанд, ки бо зиёд шудани раќами тартибиашон њаллашон андаке мураккаб мегардад. Барои њамин чанд машќи аввалаи дар пункт, пас аз назария омадаро шифоњї шумурдан мумкин аст. Машќњои њаллашон мураккабтар бо аломати
(*) ишорат карда мешаванд. Бо њал кардани мисолу масъалањои ќисми «Машќњои иловагї доир ба боб», ки дар охири њар як боб нисбати њар як параграф оварда мешаванд, шумо мустаќилона худро санљида метавонед, ки то кадом дараља маводи заруриро аз худ кардаед.
2
Љавобњои машќњои њар як боб дар охираш оварда мешаванд, ки ин ваќти шуморо барои санљидани дурустии љавоби ёфташуда сарфа мекунад.
Њар як пункт бо ќисми «Машќњо барои такрор» ба охир мера-сад. Азбаски шумо хатмкунанда њастед ва имтињони хаттии хатм-кунї месупоред, мисолу масъалањои ин ќисм айнан ба ин имтињон шабоњат доранд (бо назардошти назарияи то њамин дам омўхташуда). Дар тартиб додани машќњои ин ќисм вариантњои корњои хаттии имтињони хатмкунии солњои 1998-2002 истифода шудаанд. Ин имконият медињад, ки шумо тахминан чи гуна будани масъа-лањои имтињони хатмкуниро дарк кунед. Барои њамин бо исрор хоњиш карда мешавад, ки машќњои ин ќисмро њатман њал кунед.
Талаботи Стандарти давлатии маълумоти умумиро дар Тољикистон ба эътибор гирифта дар охири бобњо маълумоти таърихї оварда мешавад. Аз онњо шумо аз пайдоиши мафњумњо, истилоњњо, рамзњо ва рољеъ ба бунёдгарони анализи математикї тасаввурот њосил мекунед.
Боби сеюм, ки «Такрор» ном дорад, аз мисолу масъалањое иборат аст, ки онњо тамоми маводи мактабии синфњои V–XI –ро дар бар мегирад. Ин мавод на аз рўи омўзишиш дар ин ё он синф, балки њамчун объекти математикї ба параграфњо људо карда шудааст. Масалан, прогрессияњо, ки аз адад иборатанд, дар ќисми ададњои њаќиќї дар аввал, дар параграфи 1 оварда шудаанд. Тамоми маводи ин боб барои тайёрї ба имтињони хатмкунї пешбинї мешавад. Китобњои дарсии то њол нашршудаи муаллифони тољик ва чандин китобњои дарсии мамолики дигар њангоми навиштани ин боб истифода шудаанд.
3

Боби I
ФУНКСИЯИ ИБТИДОЇ ВА ИНТЕГРАЛ
1. ФУНКСИЯИ ИБТИДОЇ ВА ХОСИЯТЊОИ ОН
1. ТАЪРИФИ ФУНКСИЯИ ИБТИДОЇ
Мо ба омўзиши амали нави математикї – интегронї ва ќонуниятњо он шурўъ мекунем. Ин амал ба амали дифферентсиронї, яъне ёфтани њосилаи функсия, амали баръакс аст.
Аз мисол сар мекунем. Фарз мекунем, ки љисм аз рўи ќонуни
S(t) t2 2t њаракат менамояд. Яъне дар лањзаи ваќти t љисм
масофаи бо ин формула њисоб мешударо тай менамояд. Суръат ва шитоби љисмро меёбем. Чї тавре, ки медонем њосила аз масофаи
тайшуда суръат (t) буда, њосила аз суръат шитоб a(t) -ро медињад:
(t) s (t) (t2 2t) (t2 ) (2t) 2t 2 ; a(t) (t) (2t 2) 2 .
Айнан мисли њамин мисол, агар формулаи Галилей s gt2 -ро
2
гирем, ки он масофаеро, ки љисм вобаста ба ваќти t њангоми озод афтидан тай мекунад, ифода менамояд (дар лањзаи ибтидоии ваќт t 0 суръат нул аст, яъне (0) 0 ), он гоњ бо воситаи дифферентсиронї суръатро меёбем:
(t) s (t) gt .
Дифферентсиронии дуюм шитобро медињад: a(t) (t) g .
Дар механика ва техника бо масъалаи ба масъалањои овардаамон баръакс вомухўрем: шитоби нуќта a(t) (љисм њамчун нуќта ќабул карда мешавад) маълум аст, ёфтани ќонуни таѓйирёбии суръат (t) ва координата s(t) талаб карда мешавад. Бо ибораи дигар, аз рўи њосилаи маълум (t) , ки ба a(t) баробар аст, (t) -
4

ро ёфтан ва баъд аз рўи њосила s (t) , ки ба (t) баробар аст, s(t) -
ро ёфтан даркор аст.
Ин гуна масъалањо бо ёрии амали интегронї њал карда мешаванд.
Т а ъ р и ф: Функсияи F(x) дар фосилаи (a; b) барои
функсияи f(x) функсияи ибтидої номида мешавад, агар барои њамаи ќиматњои таѓйирёбандаи x аз (a; b)
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|||
|
|
|
|
|
|
F (x) |
|
|
|
|||||||
бошад. Яъне, њосилаи F(x) ба f (x) |
баробар бошад. |
|
||||||||||||||
Ёфтани функсияи ибтидоии функсияи додашударо амали |
||||||||||||||||
интегронї меноманд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
М и с о л и 1. Функсияи F(x) |
x2 |
|
дар фосилаи ( ; ) барои |
|||||||||||||
|
|
|||||||||||||||
функсияи f (x) x |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
функсияи ибтидої аст, |
чунки барои њар гуна |
|||||||||||||||
x ( ; ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
1 |
|
2 |
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
x |
|
|
|
|
2x x f (x) |
||||||
F (x) |
|
2 |
|
2 |
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x2 |
||
Ба осонї мебинем, ки, масалан, њосилаи |
|
5 низ ба x ба- |
|
2 |
|||
|
|
||
робар аст. Пас ин функсия низ функсияи ибтидої аст. Фањмост, ки ба љои 5 адади дилхоњро гирифтан мумкин аст. Мебинем, ки барои
функсияи мушаххаси f (x) x функсияњои ибтидої бешуморанд.
М и с о л и 2. Барои функсияи |
f (x) |
1 |
|
дар фосилаи (0; ) |
|||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функсияи F(x) 2 |
|
x |
функсияи ибтидої аст, |
|
чунки барои њар гуна |
||||||||||||||||
x аз (0; ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) 2 |
x 2 |
|
|
|
|
|
|
|
|
f (x) . |
|
||||||||||
|
|
|
|
2 |
|
x |
|
|
x |
|
|
|
|
|
|||||||
|
F(x) 2 |
|
C |
|
|||||||||||||||||
Айнан мисли мисоли 1, функсияи |
x |
њангоми |
|||||||||||||||||||
ќимати дилхоњи |
доимї |
|
ќабул кардани |
|
|
|
C |
|
барои |
функсияи |
|||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
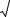
f (x) |
1 |
|
дар фосилаи (0; ) |
функсияи ибтидої мебошад. |
|
|||||||||
|
|
|
|
|||||||||||
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
М и с о л и 3. |
Функсияи |
F(x) |
|
дар фосилаи ( ; ) |
||||||||||
|
x 1 |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
барои |
функсияи |
f (x) |
|
|
|
функсияи |
ибтидої |
шуда |
||||||
(x 1)2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
наметавонад, чунки дар нуќтаи |
x 1 |
|
|
|
|
|
||||||||
баробарии F (x) f (x) љой |
||||||||||||||
надорад. Вале дар њар яке аз фосилањои ( ;1) |
ва (1; ) |
F(x) |
||||||||||||
барои f (x) функсияи ибтидої мебошад.
Э з о њ. Бар хилофи мафњуми њосила, ки дар синфи 10 дар аввал дар нуќта, баъд дар фосила муайян карда шуда буд, мафњуми функсияи ибтидої якбора дар тамоми фосила муайян мешавад.
__________________________?_______________________________
1. Њангоми дода шудани ќонуни њаракат, суръат ва шитоби он чї тавр ёфта мешавад? 2. Чї гуна масъалањо бо ёрии амали интегронї њал карда мешаванд? 3. Функсияи ибтидої чист? Таърифро бо мисолњо мукаммал намоед. 4. Чаро барои функсияи додашуда функсияњои ибтидої бешуморанд?
__________________________________________________________
1. Исбот кунед, ки функсияи F(x) дар фосилаи додашуда барои
функсияи f (x) функсияи ибтидої аст:
а) F(x) x3 , |
f (x) 3x2 , |
|
|
|
|
x ( ; ); |
|||||||
б) F(x) |
1 |
x6 , |
f (x) x5 , |
|
|
|
|
x ( ; ); |
|||||
|
|
|
|
|
|
||||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
||
в) F(x) x 4 , |
f (x) 4x 5 , |
|
|
x (0; ); |
|||||||||
г) F(x) |
1 |
x 2 , |
f (x) x 3 , |
|
|
|
|
x (0; ); |
|||||
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||
д) F(x) sin 3x , |
f (x) 3cos3x |
, |
x ( ; ); |
||||||||||
е) F(x) 1 tg |
x |
, |
f (x) |
1 |
|
|
|
, |
x ( 2 ; 2 ); |
||||
|
|
2 x |
|
||||||||||
4 |
|
|
4cos |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ( ; ); |
||||||||
ж) F(x) x |
3 |
|
21, |
|
f (x) |
3 |
|
|
|
|
x |
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
з) |
F(x) sin(2x 3) 1, f (x) 2cos(2x 3) , |
x ( ; ); |
|||||||||||||||||||||||||||||||||||||||||||||
2. Оё дар фосилаи додашуда функсияи F(x) |
барои функсияи |
||||||||||||||||||||||||||||||||||||||||||||||
f (x) функсияи ибтидої шуда метавонад: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
а) F(x) 2 cos x , |
|
f (x) sin x , |
|
|
|
|
|
x ( ; ); |
|||||||||||||||||||||||||||||||||||||||
б) |
F(x) 12 |
1 |
|
, |
|
f (x) |
1 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
x ( 1;1); |
||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
F(x) |
3 |
|
|
x |
|
|
|
|
|
|
|
f (x) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x (0; ); |
|||||||||||||||||||
в) |
3 |
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) F(x) x2 |
|
|
|
|
|
f (x) |
5 |
|
x |
|
, |
|
|
|
|
x ( ; ); |
|||||||||||||||||||||||||||||||
x |
, |
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
д) F(x) x 2 1, |
|
f (x) |
1 |
|
|
|
|
|
, |
|
|
|
|
|
|
|
x (0; ); |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
f (x) |
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
е) F(x) 1 x2 , |
|
|
|
, |
|
|
x ( 1;1) ? |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|||||||||||
3. |
Барои функсияи |
f (x) дар фосилаи |
( ; ) , яке аз функ- |
||||||||||||||||||||||||||||||||||||||||||||
сияњои ибтидоиро ёбед: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
а) |
f (x) 1,5 ; |
|
|
|
|
|
б) |
f (x) 2x ; |
|
|
|
|
|
|
|
|
|
|
|
в) |
f (x) sin x ; |
||||||||||||||||||||||||||
г) |
f (x) cos x ; |
|
|
д) |
f (x) x ; |
|
|
|
|
|
|
|
|
|
|
|
е) |
f (x) cos x ; |
|||||||||||||||||||||||||||||
ж) |
f (x) 3 ; |
|
|
|
|
|
з) |
f (x) sin x ; |
|
|
и) f (x) x2 ; |
||||||||||||||||||||||||||||||||||||
к) f (x) x5 ; |
|
|
|
|
|
л) f (x) 0 ; |
|
|
|
|
|
|
|
|
|
|
|
м) f (x) x3 . |
|||||||||||||||||||||||||||||
4. Ба љои нуќтањо ягон функсияеро гузоред, ки баробариро |
|||||||||||||||||||||||||||||||||||||||||||||||
ќаноат намояд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||
|
|
1,5; |
|
|
|
|
|
|
|
cos(x) ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
в) (...) |
x2 ; |
|||||||||||||||||||||||||||||||||||
а) |
(...) |
|
|
|
|
|
б) |
(...) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
г) |
(...) |
2 x ; |
|
|
д) |
(...) |
cos2x ; |
|
|
|
|
е) (...) |
2sin x ; |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
1 |
|
|
|
|
sin2 x ; |
|||||
ж) (...) |
з) (...) sin 4x ; |
и) (...) cos(2x 3) . |
||||
5. Ду функсияи ибтидоии функсияи |
f (x) –ро ёбед: |
|||||
а) |
f (x) 4x ; |
б) f (x) sin x 1; |
||||
в) |
f (x) x3 ; |
г) f (x) 2 cos x . |
||||
6. |
Аз се функсияи овардашуда њамонашро нишон дињед, ки |
||||||
дутои дигар мувофиќан њосила ва функсияи ибтидоии он аст: |
|||||||
а) f (x) 2, |
g(x) 2x 3, |
h(x) x2 3x 1; |
|||||
б) f (x) x 1, |
g(x) 1, |
|
|
x2 |
|||
|
h(x) |
|
x 3 ; |
||||
|
2 |
||||||
|
|
|
|
|
|
|
|
в) |
f (x) 1 sin x , g(x) |
x2 |
sin x 2 , h(x) x cos x . |
||||
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
МАШЌЊО БАРОИ ТАКРОР |
|
|
|||
7. |
Коэффитсиенти кунљии расандаро, ки ба графики функсияи |
||||||
f (x) 2x4 7x 4 |
дар нуќтаи абсиссаш |
x 1 гузаронида шуда- |
|||||
аст ёбед. |
|
|
|
|
|
|
|
8.Шитоби њаракатро ёбед, агар љисм ростхатта аз рўи ќонуни s(t) 2t2 t 3 њаракат намояд.
9.Муодиларо њал кунед:
x
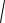 7
7 
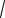 x2 6x 9 4 .
x2 6x 9 4 .
10.Функсияи y x2 (x 3) -ро бо ёрии њосила тадќиќ карда,
графикашро созед. |
|
|
|
|
11*. tg –ро ёбед, агар cos2 |
5 |
ва ( ; |
2 |
) бошад. |
|
|
|||
13 |
3 |
|
||
8 |
|
|
|
|
2. ХОСИЯТЊОИ ФУНКСИЯИ ИБТИДОЇ
Дар ин пункт намуди умумии функсияи ибтидоиро барои функсияи додашуда меёбем.
Чи тавре дидем, функсияи ибтидої ягона нест. Масалан,
|
x2 |
|
|
x2 |
|
x2 |
|
|
функсияњои |
|
5 |
ва |
|
10 , ва умуман, функсияи |
|
C барои |
|
2 |
|
2 |
|
2 |
|
|
||
њаргуна ќимати доимии C , барои f (x) x дар фосилаи |
( ; ) |
|||||||
функсияњои ибтидоианд. Зоњиран фањмост, ки фарќи ин ду функсияи ибтидої адади доимист. Нишон медињем, ки ин ба њар гуна функсияи ибтидої хос аст, яъне як функсияи ибтидої аз дигараш бо ќимати доимї фарќ мекунад. Аниќаш тасдиќи зерин дуруст аст, ки он хосияти асосии функсияи ибтидоиро ифода мекунад.
Т е о р е м а. Агар функсияи F(x) яке аз функсияи ибтидої
барои функсияи f(x) дар фосилаи (a, b) бошад, он гоњ њар гуна функсияи ибтидоии функсияи f(x) дар ин фосила намуди
F(x) С
-ро дорад, ки дар ин љо C доимии дилхоњ аст.
Пеш аз исботи теорема дурустии леммаи зеринро нишон медињем, ки он њамчун нишонаи доимї будани функсия маълум аст.
Л е м м а. Агар дар фосилаи (a; b) њосилаи функсияи F(x)
айниятан ба нул баробар бошад, яъне F (x) 0 барои њар гуна
x (a; b) , он гоњ F(x) дар ин фосила доимї аст.
И с б о т. Нуќтаи ихтиёрии x0 -ро аз фосилаи (a; b) интихоб
мекунем. Барои њар гуна x аз ин фосила, мувофиќи формулаи Лагранж, чунин нуќтаи c -и ин фосила ёфт мешавад, ки:
F(x) F(x0) F (c)(x x0) .
|
пас F(x) F(x0 ) барои |
Вале мувофиќи шарт F (c) 0 аст, |
|
њар гуна x (a;b) . Яъне функсияи F(x) |
дорои ќимати доимї аст. |
Лемма исбот шуд. |
|
И с б о т и т е о р е м а. Бигузор функсияњои (x) ва F(x) барои
функсияи f (x) дар фосилаи (a; b) функсияњои ибтидої мебошанд,
|
|
|
|
яъне барои њар гуна x (a; b) : (x) f (x) |
ва F (x) f (x) . Пас |
||
|
|
|
|
( (x) F(x)) (x) F (x) f (x) f (x) 0 .
9
Аз ин љо ва дар асоси лемма бармеояд, |
ки фарќи (x) F(x) |
|||||||||||||||
функсияест, ки дар фосилаи (a; b) доимї мебошад. Ин ќимати |
||||||||||||||||
доимиро бо С ишорат карда њосил мекунем: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
(x) F(x) С, |
|
|
|
|
|
|
|
|
|
|
(1) |
||
ки он дурустии тасдиќи теоремаро нишон медињад. |
|
|
|
|
|
|
||||||||||
Э з о њ и 1. Маънои геометрии хусусияти асосии функсияи |
||||||||||||||||
ибтидої чунин аст: графикњои ду функсияи дилхоњи ибтидоии |
||||||||||||||||
функсияи |
f (x) аз њамдигар |
бо воситаи |
ба |
самти |
|
тири |
|
|||||||||
параллел кўчонидан њосил карда мешаванд (расми 1). |
|
|
|
|
||||||||||||
|
|
|
|
|
М и с о л и 1. Зоњиран фањмост, ки |
|||||||||||
у |
|
Расми 1. |
функсияњои F(x) x2 |
ва (x) x2 4 |
||||||||||||
|
|
|
барои њамон |
як |
|
функсия |
функсияи |
|||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
ибтидоианд. |
Дар |
|
њаќиќат |
|
|
|
||||||
|
|
|
|
|
|
F (x) 2x , |
||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
(4) |
|
2x 0 2x |
|||
|
|
|
|
(x) (x 4) (x |
|
) |
|
|||||||||
|
|
|
|
ва (x) F(x) 4 . Графики (x) аз |
||||||||||||
|
|
|
|
графики параболаи F(x) бо воситаи |
||||||||||||
|
|
|
|
ба самти тири , ба боло, ба 4 во- |
||||||||||||
о |
|
|
|
њид кўчонидан њосил мешавад. |
|
|||||||||||
|
|
х |
|
Э з о њ и |
|
2. |
Тасдиќи теорема ду |
|||||||||
|
|
|
|
|
||||||||||||
хосияти функсияи ибтидоиро дарбар мегирад: 1) Њангоми дар |
||||||||||||||||
баробарии (1) ба љои С гузоштани адади дилхоњ функсияи ибтидої |
||||||||||||||||
њосил мешавад; 2) Њангоми дода шудани яке аз функсияњои |
||||||||||||||||
ибтидоии |
F(x) , њатман чунин адади С-ро ёфтан мумкин аст, ки |
|||||||||||||||
дигараш бо баробарии (1) ифода мешавад. |
|
|
|
|
|
|
|
|
|
|
|
|||||
М и |
с о |
л и |
2. |
Нишон |
медињем, |
ки |
|
фарќи |
|
функсияњои |
||||||
F(x) cos2x |
ва (x) cos2 x |
дар фосилаи ( ; ) |
|
доимї аст. |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ин доимиро меёбем. Азбаски |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
cos2x |
|
2 |
|
|
||||||
F |
(x) (x) |
|
|
cos |
|
x |
|
|
( sin 2x) 2 |
|
2 |
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
||
2cos x(cos x) sin 2x 2cos x( sin x) sin 2x 2sin xcos x
sin 2x sin 2x 0 Пас мувофиќи тасдиќи теорема:
10
