
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Завдання для самостійної роботи
Обчислити інтеграли:
1.
 ;
;
2.
 ;
;
3.
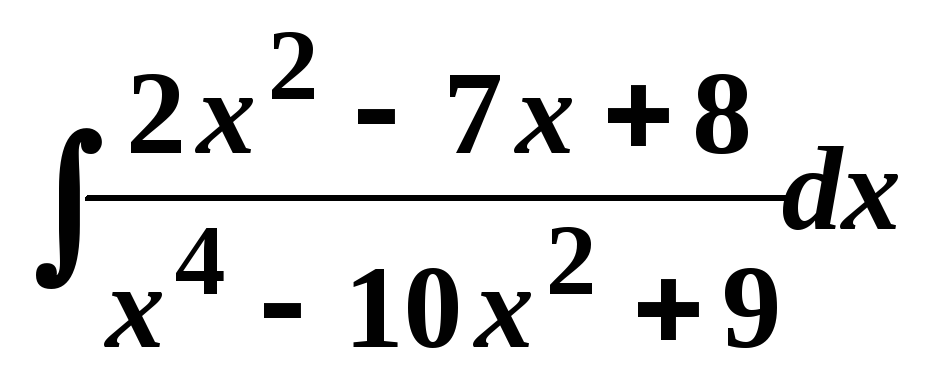 ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
 ;
;
7.
 ;
;
8.
![]() .
.
3.5. Інтегрування функцій, раціонально залежних від тригонометричних
Домовимось
позначати
![]() - раціональну функцію, залежну від
- раціональну функцію, залежну від![]() ,
якщо вона утворена з цих тригонометричних
функцій та сталих за допомогою
раціональних алгебраїчних дій.
,
якщо вона утворена з цих тригонометричних
функцій та сталих за допомогою
раціональних алгебраїчних дій.
1)
Інтеграли виду
![]() приводяться до інтегралів від
раціональної функції нового аргументу
приводяться до інтегралів від
раціональної функції нового аргументу![]() підстановкою
підстановкою
![]() ,
яка називається універсальною.
,
яка називається універсальною.
При цьому використовуються формули:
![]() ,
,
 ,
,![]() ,
,![]() .
.
Варто помітити, що недоліком цієї підстановки є той факт, що її використання в багатьох випадках зводить вихідний інтеграл до інтегралу від раціонального дробу з великими степенями. Тому в багатьох випадках користуються іншими підстановками . Наведемо деякі з них:
а)
![]() ,
тобто підінтегральна функція непарна
відносно
,
тобто підінтегральна функція непарна
відносно![]() .
Використовується підстановка
.
Використовується підстановка![]() ,
тоді
,
тоді![]() ,
, ;
;
б)
![]() - підінтегральна функція непарна
відносно
- підінтегральна функція непарна
відносно![]() .
.
Використовується
підстановка
![]() ,
тоді
,
тоді![]() ,
, ;
;
в)
![]() ,
в якому підінтегральна функція парна
відносно
,
в якому підінтегральна функція парна
відносно![]() і
і![]() одночасно, раціоналізується за допомогою
підстановки
одночасно, раціоналізується за допомогою
підстановки![]() .
При цьому використовуються формули:
.
При цьому використовуються формули:
 ,
,
![]() ,
,![]() ,
,![]() ;
;
г)
![]() .
Тут підінтегральна функція залежить
раціональним образом тільки від
.
Тут підінтегральна функція залежить
раціональним образом тільки від![]() .
Слід застосовувати підстановку
.
Слід застосовувати підстановку![]() ,
тоді
,
тоді![]() ,
,![]() .
.
2)
Інтеграли виду
![]() обчислюються за допомогою таких
підстановок:
обчислюються за допомогою таких
підстановок:
а)
якщо
![]() - ціле додатне непарне число:
- ціле додатне непарне число:![]() ;
;
б)
якщо
![]() - ціле додатне непарне число:
- ціле додатне непарне число:![]() ;
;
в)
якщо
![]() та
та![]() - цілі додатні парні числа: використовуються
формули пониження степеня
- цілі додатні парні числа: використовуються
формули пониження степеня
![]() ,
,
![]() ;
;
г)
якщо
![]() та
та![]() - цілі парні числа, але хоч одне з них
від’ємне:
- цілі парні числа, але хоч одне з них
від’ємне:
![]() ;
;
д)
якщо
![]() та
та![]() - цілі непарні числа і від’ємні:
- цілі непарні числа і від’ємні:![]() .
.
3)
Інтеграли виду
![]() ,
,![]() ,
,![]() обчислюються за допомогою тригонометричних
формул:
обчислюються за допомогою тригонометричних
формул:
![]() ,
,
![]() ,
,
![]() .
.
Зразки розв’язування задач
Обчислити інтеграли.
Почнемо з прикладів ілюструючих різні випадки пункту 1.
 .
.
Застосуємо
до інтеграла універсальну підстановку
![]() ,
,![]() ,
, .
.
Тоді

 .
.
2.


 .
.
3.



![]() .
.
4.
 .
.
Зауважимо
на те, що підінтегральна функція непарна
відносно
![]() .
Відділимо від
.
Відділимо від![]() один множник, а
один множник, а![]() виразимо через
виразимо через![]() ,
а саме:
,
а саме:![]() .
Інтеграл матиме вигляд:
.
Інтеграл матиме вигляд: ,
тобто ми звели його до випадку
,
тобто ми звели його до випадку![]() ,
до якого можна застосувати заміну
,
до якого можна застосувати заміну![]() ,
,![]() .
.
Отримаємо:

 .
.
5.
 .
.
Підінтегральна
функція непарна відносно
![]() .
Аналогічно попередньому прикладу
.
Аналогічно попередньому прикладу![]() .
.
Отже,

 .
.
Зауваження:
отриманий інтеграл
![]() може бути обчислений іншим методом за
допомогою формул тригонометрії, а саме:
може бути обчислений іншим методом за
допомогою формул тригонометрії, а саме:
![]() .
.
6.
![]() .
.
Так
як підінтегральна функція є раціональною
функцією від
![]() та
та![]() ,
зручною є заміна
,
зручною є заміна![]() ,
,![]() .
Тоді
.
Тоді ,
,![]() .
Підставимо вирази в інтеграл і отримаємо:
.
Підставимо вирази в інтеграл і отримаємо:


![]() .
.
7.
 .
.
В
цьому випадку зручнішою буде підстановка
![]() ,
,![]() .
Перетворивши підінтегральний вираз
та використавши наведену підстановку,
отримаємо:
.
Перетворивши підінтегральний вираз
та використавши наведену підстановку,
отримаємо:
 .
.
8.
![]() .
.
Підінтегральна
функція є раціональною функцією відносно
![]() .
Зробимо заміну
.
Зробимо заміну![]() ,
,![]() .
.
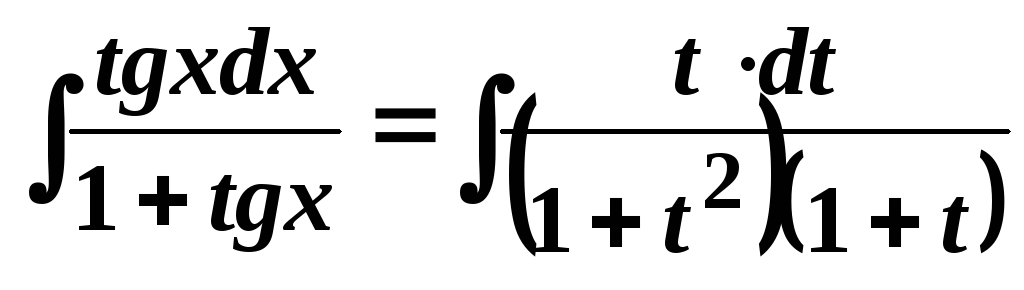 .
Останній інтеграл є інтегралом від
правильного раціонального дробу. Для
інтегрування розкладемо дріб на суму
найпростіших:
.
Останній інтеграл є інтегралом від
правильного раціонального дробу. Для
інтегрування розкладемо дріб на суму
найпростіших:
 ,
,
![]() .
.
Порівнюючи
коефіцієнти при однакових степенях
![]() в обох частинах рівності, отримаємо:
в обох частинах рівності, отримаємо:
![]() ,
,![]() .
Отже,
.
Отже,

![]()
![]() .
.
9.
![]() .
.
Підінтегральна
функція непарна відносно
![]() ,
тому інтеграл можна звести до інтегралу
від раціональної функції підстановкою
,
тому інтеграл можна звести до інтегралу
від раціональної функції підстановкою![]() ,
,![]() ;
;![]() ,
, .
Отримаємо:
.
Отримаємо: .
.
Після
розкладання дробу
 на суму найпростіших одержимо:
на суму найпростіших одержимо:
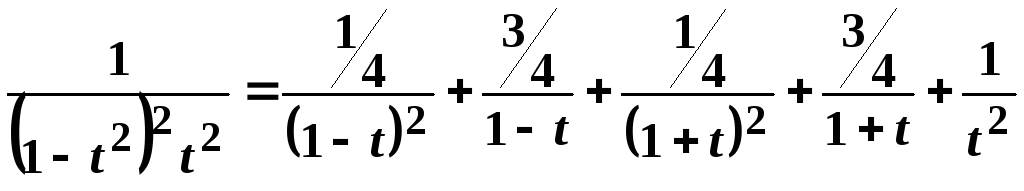 .
.
Коефіцієнти
розкладання
![]() обчислюються звичними методами і
дорівнюють:
обчислюються звичними методами і
дорівнюють:![]() ,
,![]() ,
,![]() .
Тоді інтеграл дорівнюватиме:
.
Тоді інтеграл дорівнюватиме:




 .
.
Далі розглянемо приклади різних випадків пункту 2.
10.
 (тут
(тут![]() - ціле додатне непарне).
- ціле додатне непарне).
При
заміні
![]() на
на![]() підінтегральна функція не змінює знак.
підінтегральна функція не змінює знак.
Тут
доцільна підстановка
![]() ,
,![]() ,
,![]() .
.

 .
.
11.
![]() (
(![]() ,
,![]() - ціле додатне непарне число).
- ціле додатне непарне число).

 .
.
12.
![]() .
.
Підінтегральна
функція містить тільки парний степінь
синуса, який допускає пониження степеня
за формулою:
 .
Отже,
.
Отже,
![]()
![]() .
.
13.
![]() (
(![]() ,
,![]() - ціле парне від’ємне число).
- ціле парне від’ємне число).
 .
.
Застосуємо
заміну
![]() ,
,![]() ,
,![]() .
Тоді
.
Тоді
![]() .
.
14.
![]() .
.
Показники
![]() і
і![]() обидва парні від’ємні. Зручною буде
заміна
обидва парні від’ємні. Зручною буде
заміна![]() ,
,![]() ,
, ,
,![]() .
Після підстановки інтеграл набуває
вигляду:
.
Після підстановки інтеграл набуває
вигляду:


![]() .
.
15.
 .
.
Показники
![]() і
і![]() обидва непарні. Можна знову застосувати
заміну
обидва непарні. Можна знову застосувати
заміну![]() .
.


 .
.
Перейдемо до розглядання прикладів до пункту 3.
16.![]() .
.
Перетворимо
добуток тригонометричних функцій в
суму згідно з наведеною формулою:
![]() .
Проінтегруємо
отриманий вираз:
.
Проінтегруємо
отриманий вираз:
![]() .
.
17.![]()
![]() .
.
