- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
3.5 Операции над нечеткими множествами
Над нечеткими множествами можно производить различные операции, при этом необходимо определить их так, чтобы в частном случае, когда множества являются четкими, эти операции переходили в обычные операции четких множеств, рассмотренных выше. Другими словами, операции над нечеткими множествами должны обобщать соответствующие операции над четкими множествами. При этом обобщение может быть реализовано различными способами, из-за чего какой-либо операции над обычными множествами может соответствовать несколько операций в теории нечетких множеств.
Если в теории четких множеств понятие характеристической функции играет второстепенную роль, то для нечетких множеств функция принадлежности становится единственно возможным средством их описания. С формальной точки зрения нет необходимости различать нечеткое множество и его функцию принадлежности. Поэтому все операции над нечеткими множествами проводятся с соответствующими функциями принадлежности.
Логические операции.
-
Включение.
Пусть ![]() - нечеткие множества на универсальном
множестве
- нечеткие множества на универсальном
множестве ![]() .
Говорят, что
.
Говорят, что ![]() ,
если
,
если
![]() .
(3.5)
.
(3.5)
Включение
обозначается, как ![]() .
Иногда используют термин доминирование,
то есть в случае, когда
.
Иногда используют термин доминирование,
то есть в случае, когда ![]() ,
говорят, что
,
говорят, что ![]() .
.
Помимо определенной выше операции включения, которую можно назвать четким включением, вводится операция нечеткого включения.
-
Определение.
Степень
включения
нечеткого множества ![]() в нечеткое множество
в нечеткое множество ![]() определяется по формуле
определяется по формуле
![]() (3.6)
(3.6)
Если
![]() ,
то нечеткое множество
,
то нечеткое множество ![]() нечетко включается в нечеткое множество
нечетко включается в нечеткое множество
![]() .
Если
.
Если ![]() ,
то
,
то ![]() нечетко не включается в
нечетко не включается в ![]() .
Нечеткое включение обозначается как
.
Нечеткое включение обозначается как
![]() ,
а не включение – как
,
а не включение – как ![]() .
.
Пример. Пусть даны два нечетких множества
![]() ,
,
![]() .
.
Требуется
определить степень нечеткого включения
множества ![]() во множество
во множество ![]() .
.
Решение. Согласно определению возьмем операцию конъюнкции по всем возможным парам элементов
![]() Таким образом, множество
Таким образом, множество ![]() нечетко включается в нечеткое множество
нечетко включается в нечеткое множество
![]() .
.
Самостоятельно
вычислить степень включения множества
![]() во множество
во множество ![]() .
Ответ
.
Ответ ![]() .
.
Имеет
место следующее утверждение: если
нечеткое множество ![]() включается в нечеткое множество
включается в нечеткое множество ![]() ,
то выполняется и нечеткое включение;
обратное утверждение не выполняется.
,
то выполняется и нечеткое включение;
обратное утверждение не выполняется.
Доказательство.
Пусть на универсальном множестве ![]() определены два нечетких множества
определены два нечетких множества ![]() ,
докажем, что
,
докажем, что ![]() .
.
Если
![]() ,
то
,
то
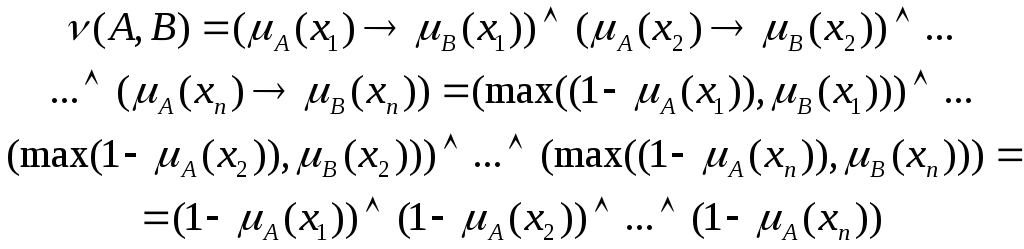
Из
определения операции конъюнкции следует,
результат будет минимальным из всех ![]() .
Поскольку по условию
.
Поскольку по условию
![]() ,
то
,
то ![]() .
.
Рассмотрим второй случай, когда
![]() .
.
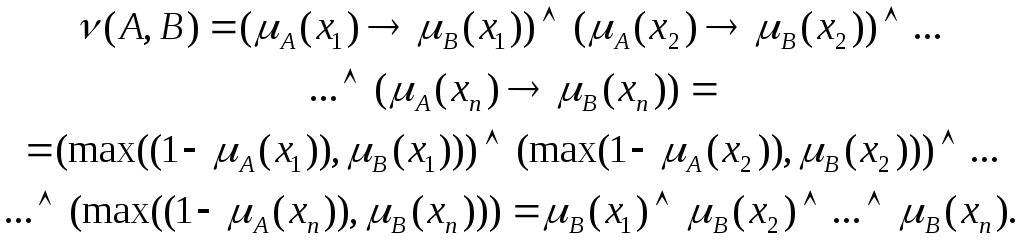
Тогда
![]() .
.
Если
выполняется только условие ![]() ,
то из этого не следует, что
,
то из этого не следует, что
![]() .
.
-
Равенство.
Множества ![]() равны,
если
равны,
если
![]() .
(3.7)
.
(3.7)
Равенство
записывается как ![]() .
.
Вводится понятие нечеткого равенства.
- Определение. Степень нечеткого равенства определяется как
![]() .
(3.8)
.
(3.8)
Если
![]() ,
то множества нечетко равны и обозначается
как
,
то множества нечетко равны и обозначается
как ![]() .
.
Если
![]() ,
то множества нечетко не равны и
обозначается как
,
то множества нечетко не равны и
обозначается как ![]() .
.
Если
![]() ,
то множества взаимно индифферентны
,
то множества взаимно индифферентны ![]() .
.
Пример.
Пусть на универсальном множестве ![]() определены два нечетких множества
определены два нечетких множества
![]() ,
,
![]()
Определить степень равенства. Согласно определению имеем
![]()
Отсюда
следует, что множества нечетко равны
![]() .
.
Преобразуем степень равенства следующим образом:
![]() (3.9)
(3.9)
При преобразовании использовано свойство коммутативности конъюнкции.
Из формулы (3.9) следует, что степень равенства нечетких множеств равна минимальной из степеней их взаимного включения.
Если
![]() ,
то есть множества нечетко равны, тогда
,
то есть множества нечетко равны, тогда
![]() и
и
![]()
Отсюда следует метод доказательства равенства нечетких множеств, основанный на доказательстве из взаимного включения.
Утверждение,
что если нечеткие множества равны, то
есть выполняется условие ![]() ,
то эти множества являются и нечетко
равными, доказать самостоятельно.
,
то эти множества являются и нечетко
равными, доказать самостоятельно.
-
Дополнение.
Пусть ![]() нечеткие множества, заданные на
универсальном множестве
нечеткие множества, заданные на
универсальном множестве ![]() .
.
![]() дополняют друг друга, если
дополняют друг друга, если
![]() .
(3.10)
.
(3.10)
Обозначение:
![]() или
или ![]() .
Очевидно выполнение следующего
равенства
.
Очевидно выполнение следующего
равенства![]() .
.
Обычно для определения пересечения, объединения используют следующие операции:
-
Пересечение.
Пересечением двух нечетких множеств ![]() называется наибольшее нечеткое,
содержащееся одновременно в
называется наибольшее нечеткое,
содержащееся одновременно в ![]() .
Для определения пересечения используют
следующие операции:
.
Для определения пересечения используют
следующие операции:
1) максиминные
![]() .
(3.11)
.
(3.11)
Пересечение соответствует союзу и, более компактно записывается как
![]() (3.12)
(3.12)
где
символ ![]() обозначает взятие min.
обозначает взятие min.
2) ограниченные
![]() .
(3.13)
.
(3.13)
-
Объединение.
Объединением двух нечетких множеств ![]() называют нечеткое множество
называют нечеткое множество ![]() ,
включающее как
,
включающее как ![]() так и
так и ![]() .
Для определения объединения так же
используют операции:
.
Для определения объединения так же
используют операции:
1) максиминные
![]() ;
(3.14)
;
(3.14)
Объединение по максиминному типу соответствует союзу или и более компактно записывается как
![]() .
(3.15)
.
(3.15)
где
символ ![]() обозначает операцию взятия max.
обозначает операцию взятия max.
2) ограниченные
![]() .
(3.16)
.
(3.16)
- Разность. Разность определяется как максиминная операция
![]() ,
(3.17)
,
(3.17)
с функцией принадлежности
![]() .
(3.18)
.
(3.18)
- Дизъюнктивная сумма
![]() ,
(3.19)
,
(3.19)
с функцией принадлежности
 (3.20)
(3.20)
Примеры. Пусть
![]() ;
;
![]() ;
;
![]() .
.
Здесь:
1)
![]() ,
то есть
,
то есть ![]() содержится в
содержится в ![]() или
или ![]() доминирует
доминирует ![]() ;
;
![]() несравнимо
ни с
несравнимо
ни с ![]() ,
ни с
,
ни с ![]() ,
другими словами, пары
,
другими словами, пары ![]() и
и ![]() -пары
недоминируемых нечетких множеств.
-пары
недоминируемых нечетких множеств.
2)
![]() .
.
3)
![]() ;
;
![]() ;
;
![]() .
.
4)
![]() =
=![]() =
=
=
=![]() .
.
5)
![]() =
=![]() =
=
=![]()
6)
![]() =
=
=
=![]() =
=
=![]() ;
;
![]() =
=
=
=![]() =
=
=![]() .
.
7)
![]() =
=
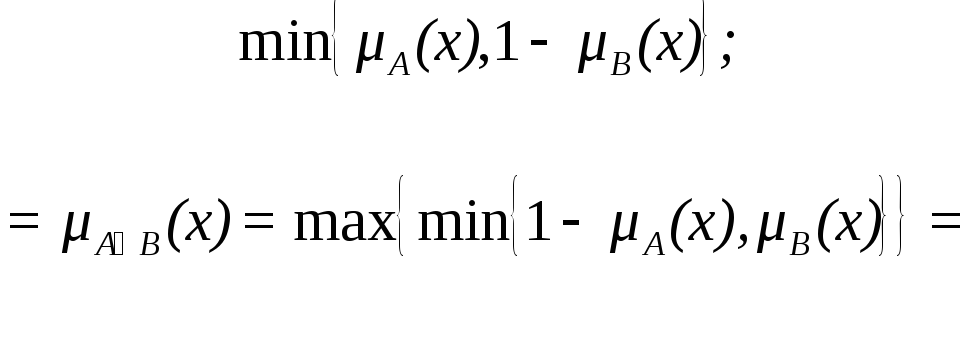
![]() .
.
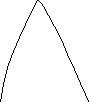
Логические
операции над нечеткими множествами
можно изобразить геометрически.
Рассмотрим прямоугольную систему
координат, на оси ординат которой
откладываются значение ![]() ,
а на оси абсцисс элементы универсального
множества
,
а на оси абсцисс элементы универсального
множества ![]() .
Графическое представление делает более
наглядным простые логические операции
над нечеткими множествами.
.
Графическое представление делает более
наглядным простые логические операции
над нечеткими множествами.



![]()
![]()
![]()
А
![]()
Х

Свойство операций объединения и пересечения.
Пусть
![]() - нечеткие множества, тогда выполняются
следующие свойства:
- нечеткие множества, тогда выполняются
следующие свойства:
1)
коммутативность
 ;
(3.21)
;
(3.21)
2)
ассоциативность
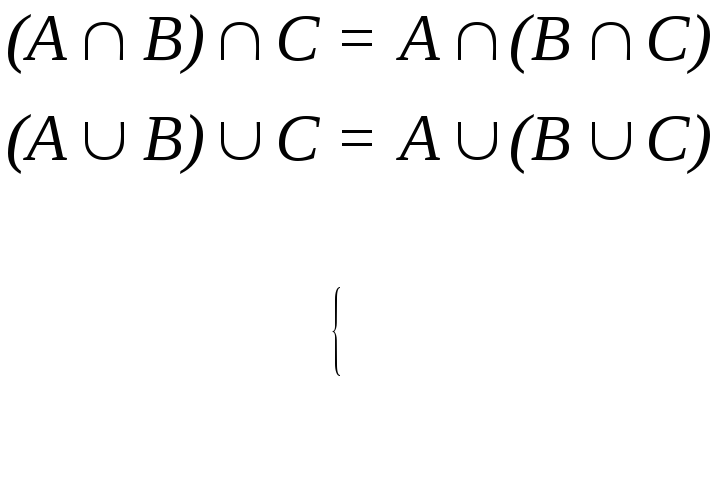 ;
(3.22)
;
(3.22)
3)
идемпотентность
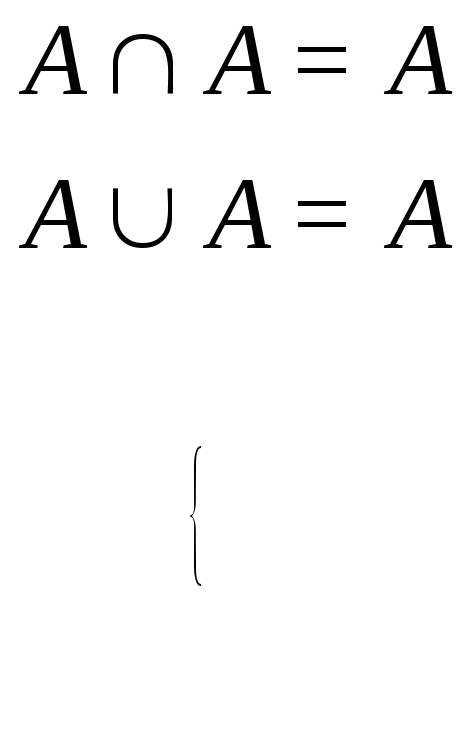 ;
(3.23)
;
(3.23)
4) дистрибутивность
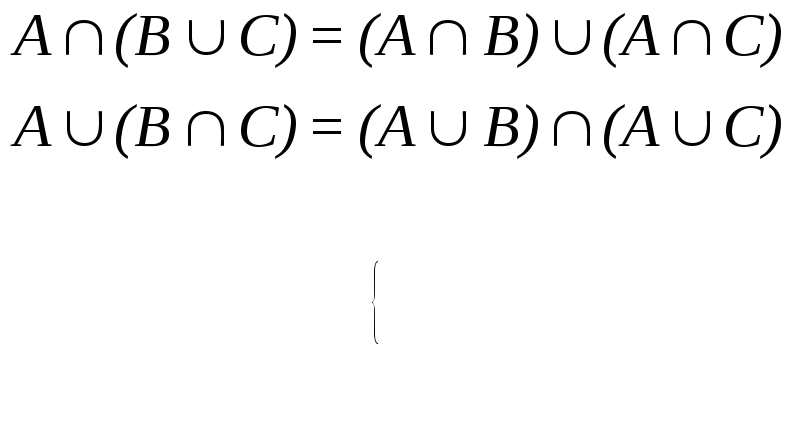 ;
(3.24)
;
(3.24)
5)
![]() ,
где
,
где ![]() -
пустое множество, то есть
-
пустое множество, то есть
![]()
![]() ;
(3.25)
;
(3.25)
6)
![]() ;
(3.26)
;
(3.26)
7)
![]() ;
(3.27)
;
(3.27)
8)
![]() ;
(3.28)
;
(3.28)
9)
теоремы де Моргана  .
(3.29)
.
(3.29)
В отличие от четких множеств, для нечетких в общем случае имеет место:
![]() ;
;
![]() .
(3.30)
.
(3.30)
Следует отметить, что введенные выше операции и свойства основаны на использовании операции min и max.
Алгебраические операции над нечеткими множествами.
Алгебраическим
произведением нечетких множеств
![]() называется
нечеткое множество
называется
нечеткое множество ![]() ,
определяемое как
,
определяемое как
![]()
![]()
![]() .
(3.31)
.
(3.31)
Алгебраическая
сумма этих множеств
называется множество ![]() ,
определяемое как
,
определяемое как
![]()
![]() .
(3.32)
.
(3.32)
Для алгебраических операций произведения и суммы выполняются следующие свойства:
коммутативность
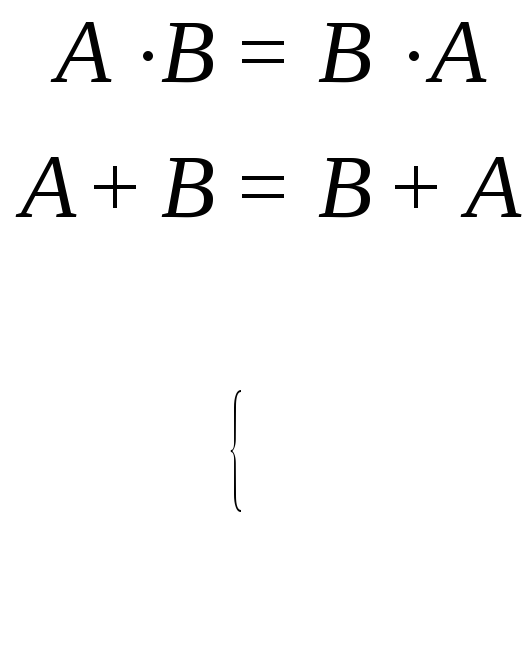 ;
(3.33)
;
(3.33)ассоциативность
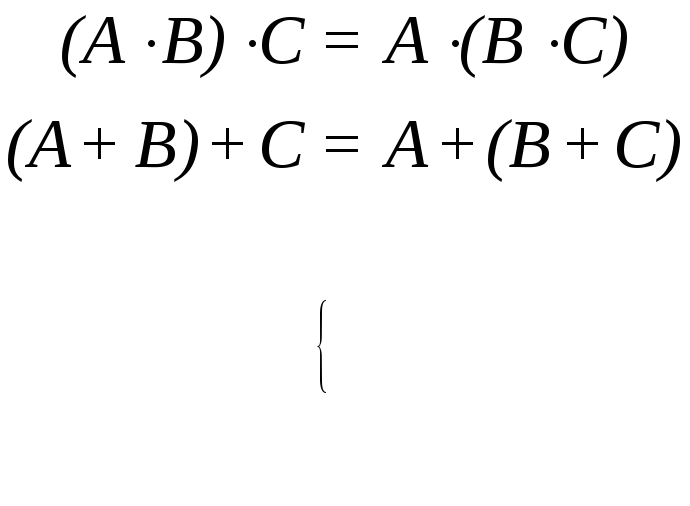 (3.34)
(3.34) ,
,
 ,
,
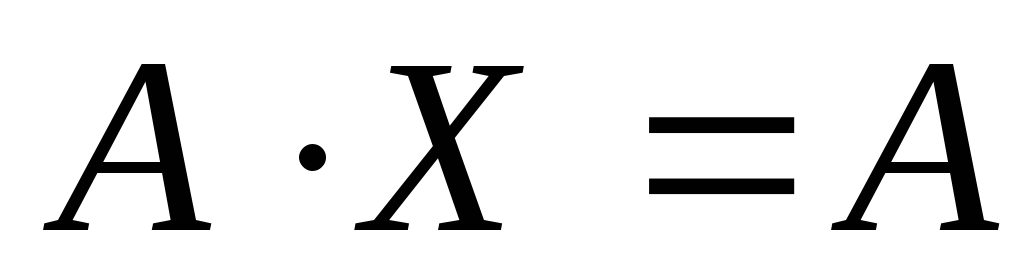 ,
,
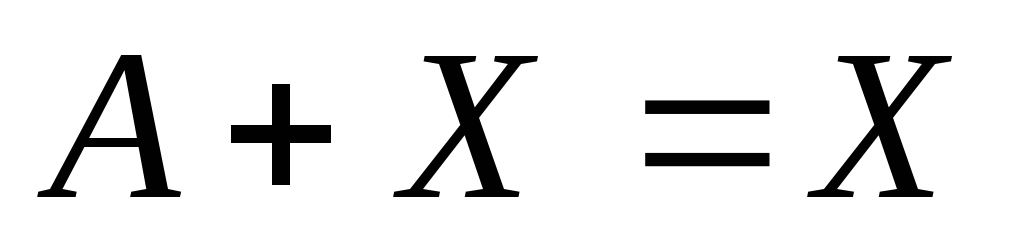 ;
;Теоремы де Моргана
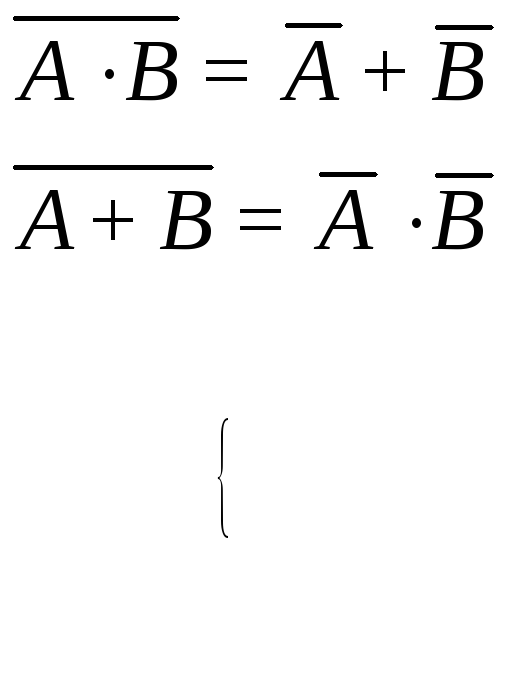 .
(3.35)
.
(3.35)
Не выполняются:
идемпотентность
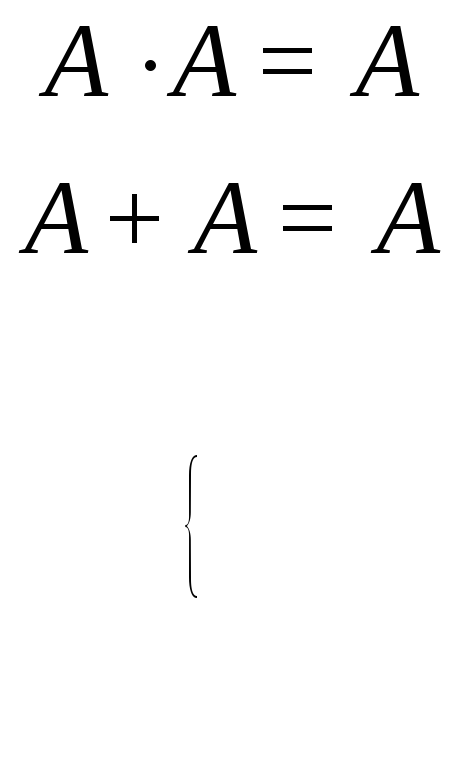 ;
(3.36)
;
(3.36)дистрибутивность
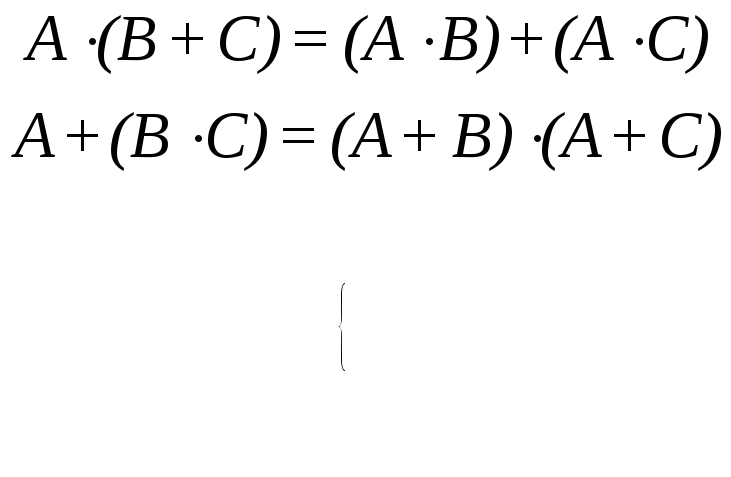 ; (3.37)
; (3.37)а также
 ,
,
 .
(3.38)
.
(3.38)
При
совместном использовании логических
операций ![]() и алгебраических
и алгебраических ![]() выполняются следующие свойства:
выполняются следующие свойства:
1)
![]() ;
(3.39)
;
(3.39)
2)
![]() ;
(3.40)
;
(3.40)
3)
![]() ;
(3.41)
;
(3.41)
4)
![]() .
(3.42)
.
(3.42)
На
основании алгебраического произведения
определяется операция возведение в
степень ![]() нечеткого множества, где
нечеткого множества, где ![]() -
положительное число. Нечеткое множество
-
положительное число. Нечеткое множество
![]() определяется
функцией принадлежности
определяется
функцией принадлежности ![]() .
Частным случаем возведения в степень
являются:
.
Частным случаем возведения в степень
являются:
операция концентрирования (уплотнения) -
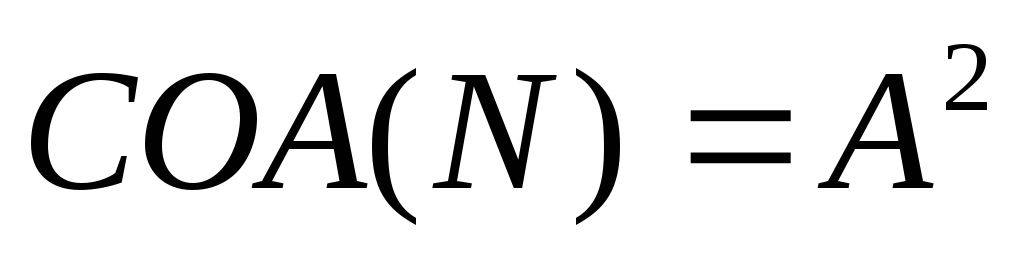 ;
;операция растяжения -
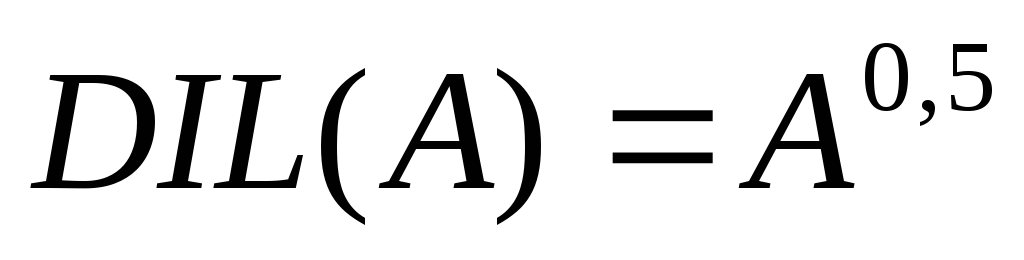 ,
,
которые используются при работе с лингвистическими неопределенностями.
Умножение
на число. Если
![]() - положительное число, такое, что
- положительное число, такое, что ![]() ,
то нечеткое множество
,
то нечеткое множество ![]() имеет функцию принадлежности
имеет функцию принадлежности
![]() .
.
Выпуклая
комбинация нечетких множеств.
Пусть ![]() - нечеткие множества универсального
множества
- нечеткие множества универсального
множества ![]() ,
а
,
а ![]() - неотрицательные числа, сумма которых
равна 1. тогда выпуклой комбинацией
называется нечеткое множество с функцией
принадлежности
- неотрицательные числа, сумма которых
равна 1. тогда выпуклой комбинацией
называется нечеткое множество с функцией
принадлежности
![]()
![]() .
(3.43)
.
(3.43)
Декартово
(прямое) произведение нечетких множеств.
Пусть ![]() - нечеткие множества соответствующих
универсальных множеств
- нечеткие множества соответствующих
универсальных множеств ![]() .
Декартово (прямое) произведение
.
Декартово (прямое) произведение ![]() является нечеткое подмножество множества
является нечеткое подмножество множества
![]() c
функцией принадлежности
c
функцией принадлежности
![]() (3.44)
(3.44)
Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.
Пусть
![]() - нечеткое множество,
- нечеткое множество, ![]() - универсальное множество и для всех
- универсальное множество и для всех ![]() определены нечеткие множества
определены нечеткие множества ![]() .
Совокупность всех
.
Совокупность всех ![]() называется ядром увеличения нечеткости
называется ядром увеличения нечеткости
![]() .
Результатом действия оператора
.
Результатом действия оператора ![]() на нечеткое множество
на нечеткое множество ![]() будет нечеткое множество следующего
вида
будет нечеткое множество следующего
вида
![]() ,
(3.45)
,
(3.45)
где
![]() - произведение числа на нечеткое
множество.
- произведение числа на нечеткое
множество.
Пример.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда