- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
5.4 Равносильные формулы логики предикатов
Рассматривая
формулы логики предикатов над полем ![]() можно говорить о формулах, равносильных
над данным полем, то есть о таких формулах,
которые принимают одно и то же значение
при замене свободных предметных
переменных предметами и всех переменных
предикатов – определенными.
можно говорить о формулах, равносильных
над данным полем, то есть о таких формулах,
которые принимают одно и то же значение
при замене свободных предметных
переменных предметами и всех переменных
предикатов – определенными.
Пример.
Рассмотрим формулы ![]() и
и ![]() над полями
над полями ![]() и
и ![]() .
.
Пусть
![]() и
и ![]() даны над полем
даны над полем ![]() .
Значениями переменного предиката
.
Значениями переменного предиката ![]() могут быть два определенных предиката
могут быть два определенных предиката
![]() и
и
![]() (см. табл.)
(см. табл.)
Предикаты
над полем ![]()
-
x
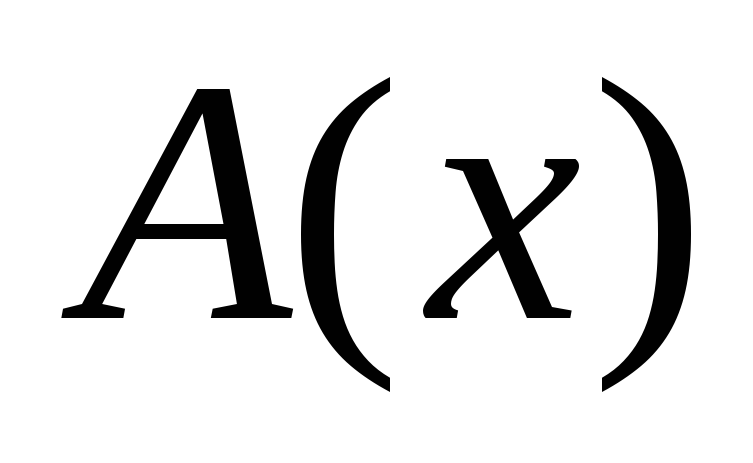
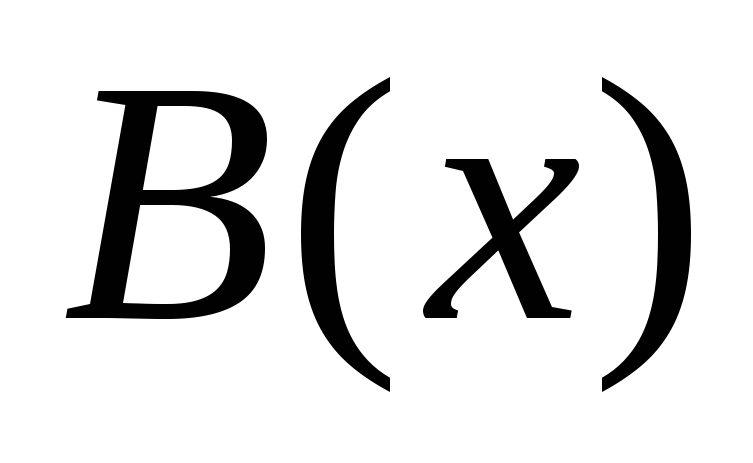

0
1
Равносильность
над полем ![]()
-
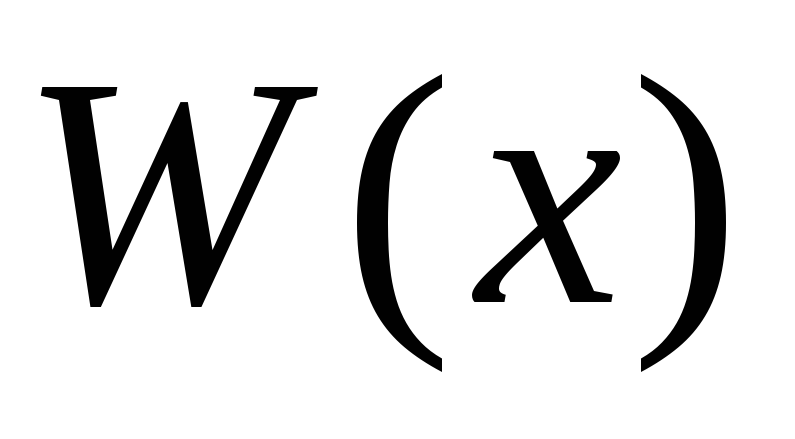
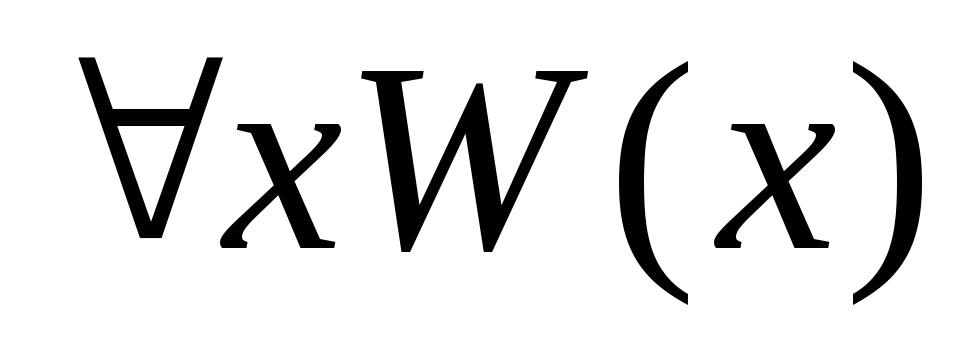
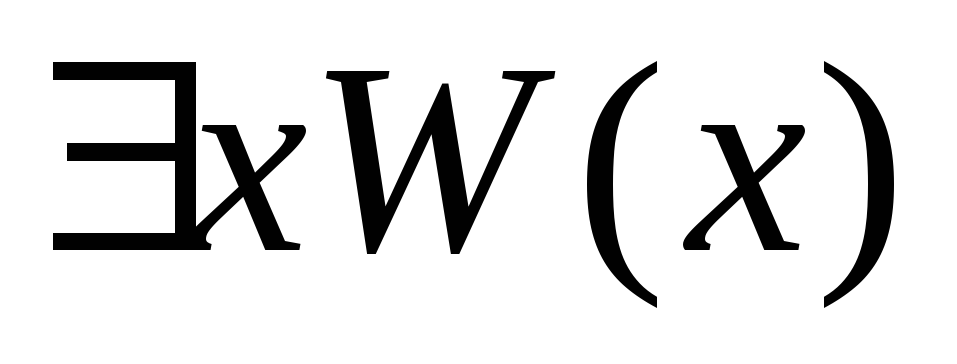
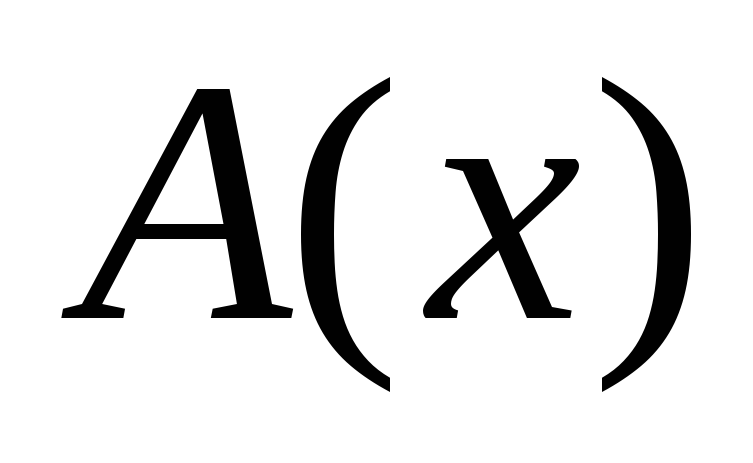
0
0

1
1
Пусть
теперь формулы ![]() и
и ![]() даны над полем
даны над полем ![]() .
В качестве значений переменного предиката
.
В качестве значений переменного предиката
![]() нужно взять определенные предикаты над
полем
нужно взять определенные предикаты над
полем ![]() .
Таких предикатов существует четыре
(см. табл.). Составив истинностную таблицу
формул
.
Таких предикатов существует четыре
(см. табл.). Составив истинностную таблицу
формул ![]() и
и ![]() ,
легко убедиться в них неравносильности
над полем
,
легко убедиться в них неравносильности
над полем ![]() .
.
Предикаты
над ![]() .
.
-
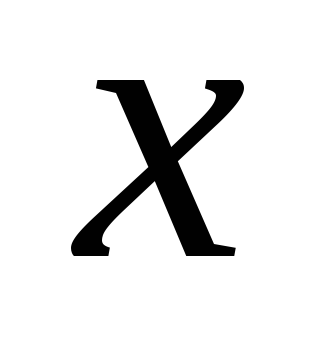
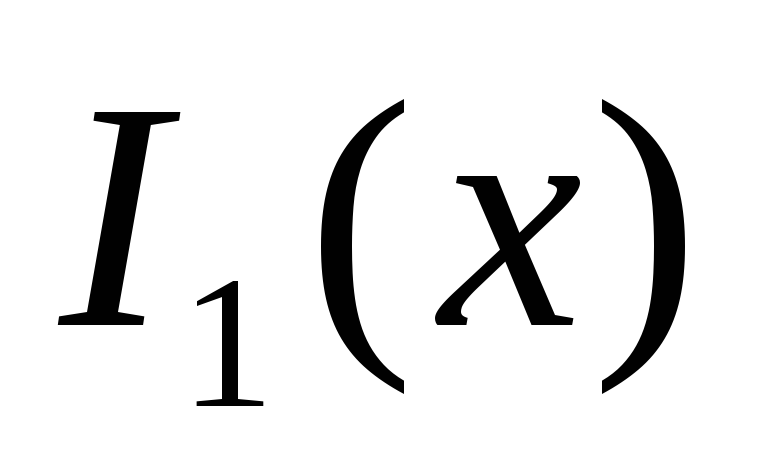
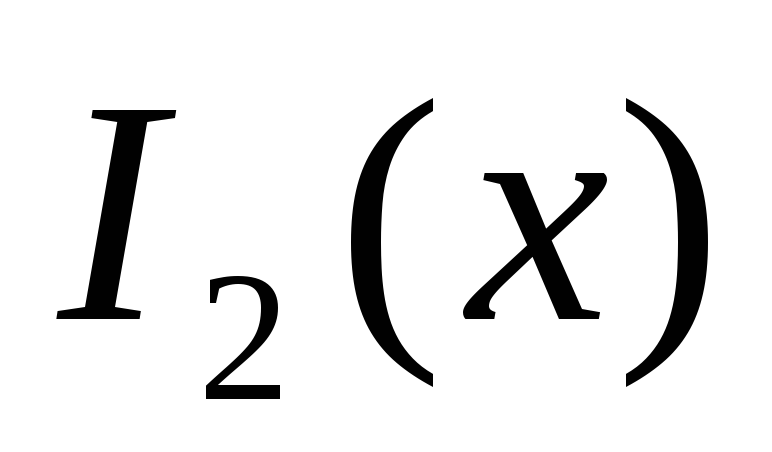
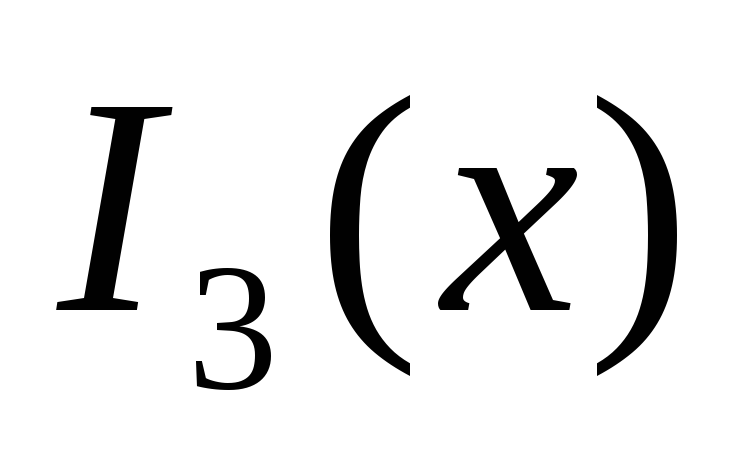
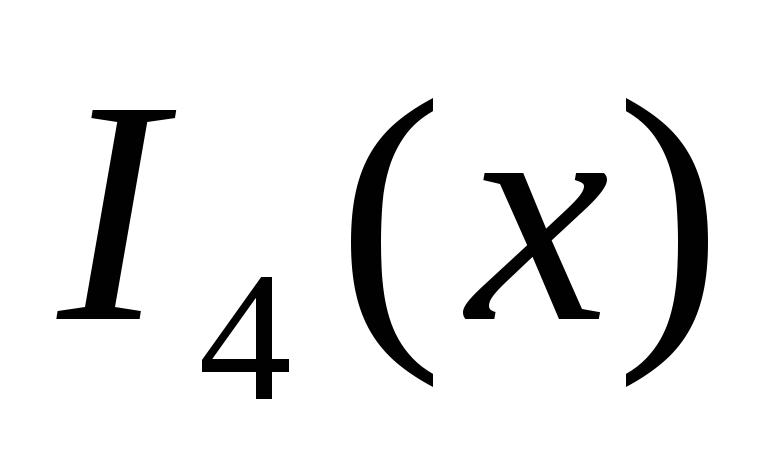

0
0
1
1

0
1
0
1
Неравносильность
над ![]() .
.
-
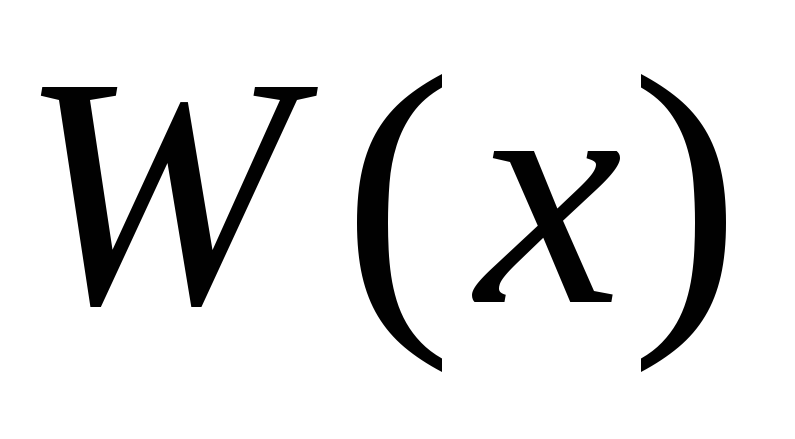
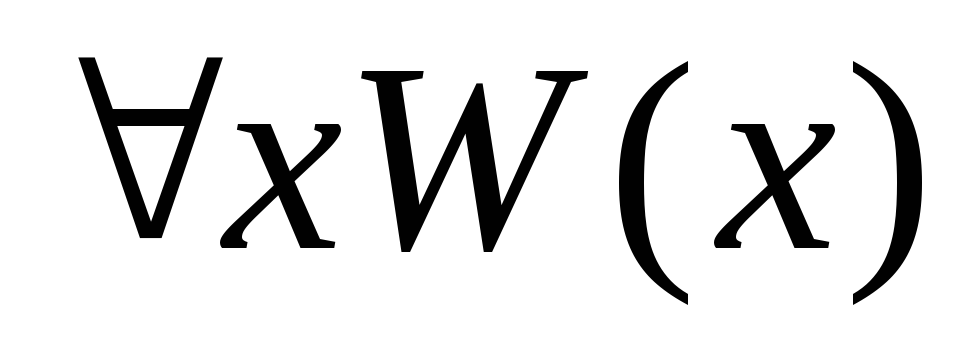
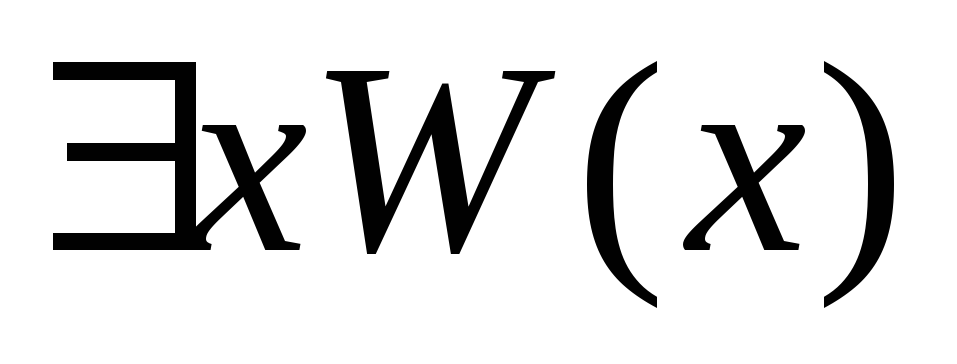
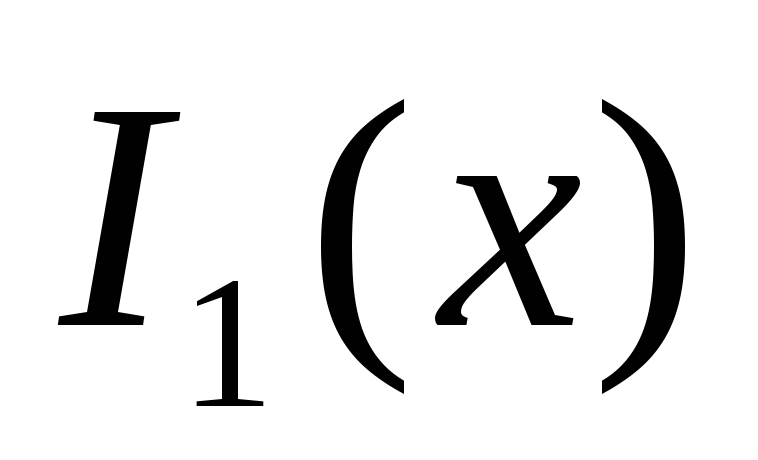
0
0
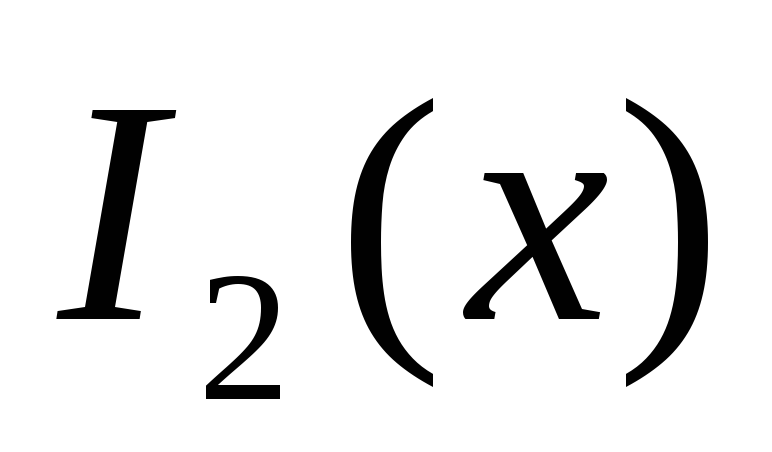
0
1

0
1

1
1
Формулы предикатов называются равносильными, если они равносильны над любым полем. Приведем примеры равносильных формул:
1) И ;
2) И ;
3) И ;
4) И .
Докажем
равносильность первой пары формул.
Пусть ![]() - произвольное поле, а
- произвольное поле, а ![]() - некоторый определенный предикат над
этим полем. Подставим вместо переменного
предиката
- некоторый определенный предикат над
этим полем. Подставим вместо переменного
предиката ![]() определенный предикат
определенный предикат ![]() .
Пусть высказывание
.
Пусть высказывание ![]() истинное, тогда высказывание
истинное, тогда высказывание ![]() ложное. Следовательно, существует
предмет
ложное. Следовательно, существует
предмет ![]() из поля
из поля ![]() ,
что
,
что ![]() ложно,
тогда
ложно,
тогда ![]() - истинно. Значит, высказывание
- истинно. Значит, высказывание ![]() истинно. Аналогичными рассуждениями
получим, что из предположения ложности
высказывания
истинно. Аналогичными рассуждениями
получим, что из предположения ложности
высказывания ![]() следует ложность высказывания
следует ложность высказывания ![]() .
.
Среди
всех формул логики предикатов можно
выделить формулы, истинные над любым
полем, их называют тождественными.
Например, формула ![]() является тождественно-истинной.
является тождественно-истинной.
В общем случае выяснить вопрос, является ли данная формула тождественно-истинной, сложно, так как приходится использовать понятие бесконечности.
5.5 Нечеткая логика
Так же как в основе теории четких множеств лежит четкая логика, в случае нечетких множеств существует нечеткая логика – основа для операций, рассмотренных выше. В случае двузначной четкой логики существуют полные системы, образованные операциями НЕ-И-ИЛИ, НЕ-И и НЕ-ИЛИ. С их помощью можно записать все другие логические операции. В случае нечеткой логики можно создать неограниченное число операций, поэтому нет смысла говорить о записи всех операций с помощью некоторого числа базовых операций, поэтому рассмотрим только наиболее важные из них.
Нечеткие высказывания и операции над ними
Нечеткая истинность. Особое место в нечеткой логике занимает лингвистическая переменная «истинность» относительно некоторого нечеткого высказывания.
Определение.
Нечетким высказыванием ![]() называют предложение, относительно
которого можно судить о степени его
истинности или ложности
называют предложение, относительно
которого можно судить о степени его
истинности или ложности ![]() ,
принимающей значение из интервала [0,1]
,
принимающей значение из интервала [0,1]
В классической логике истинность может принимать только два значения: истинно и ложно. В нечеткой логике истинность размыта. Нечеткая истинность определяется аксиоматически, причем разными авторами по-разному. Интервал [0,1] используется как универсальное множество для задания лингвистической переменной «истинность». Четкая истинность может быть представлена функцией принадлежности следующего вида
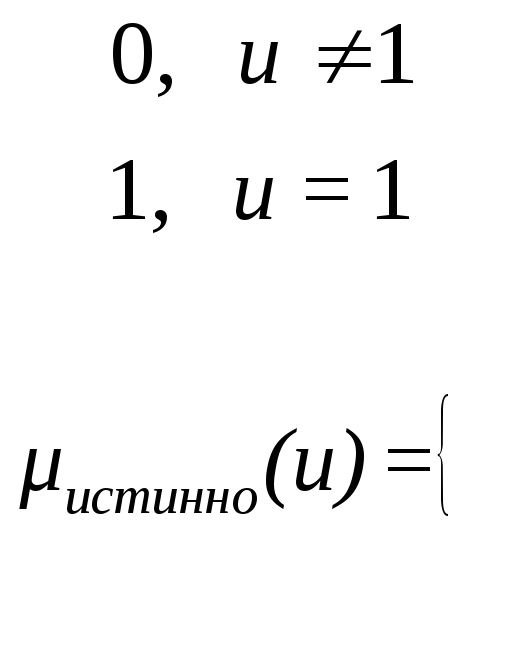 ,
,
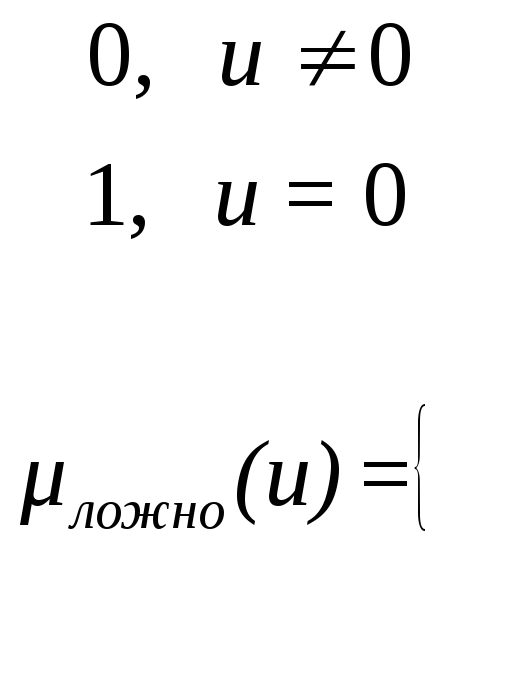 ,
,
где
![]() .
.
Обозначим
нечеткие логические переменные через
![]() и
и ![]() ,
а функции принадлежности, задающие
истинностные значения этих переменных
- через
,
а функции принадлежности, задающие
истинностные значения этих переменных
- через ![]() и
и ![]() ,
,
![]() .
Нечеткие логические операции: конъюнкция
«И» - (
.
Нечеткие логические операции: конъюнкция
«И» - (![]() );
дизъюнкция «ИЛИ» -
);
дизъюнкция «ИЛИ» - ![]() ;
отрицание «НЕ» - (
;
отрицание «НЕ» - (![]() );
импликация (
);
импликация (![]() )
выполняются по следующим правилам.
)
выполняются по следующим правилам.
конъюнкция двух нечетких высказываний
 и
и 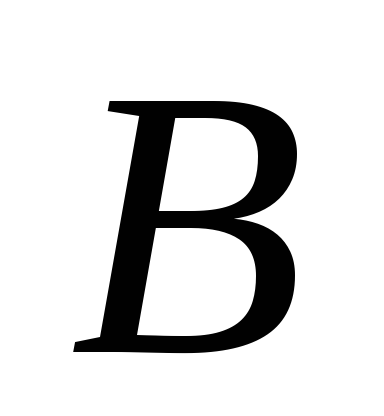 обозначается как
обозначается как 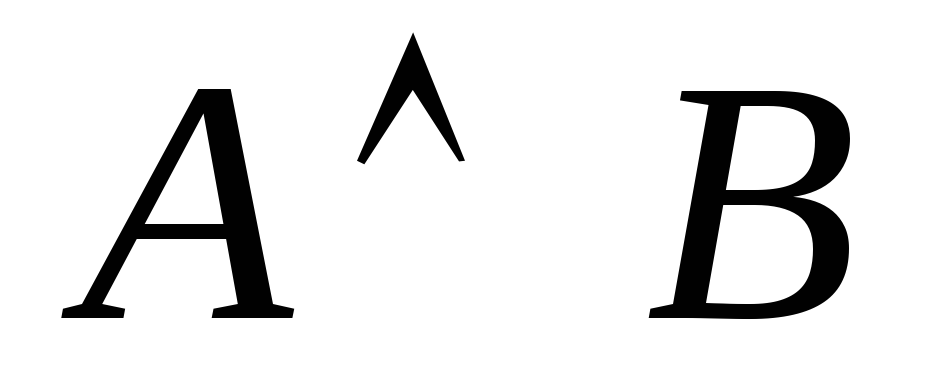 и имеет степень истинности
и имеет степень истинности 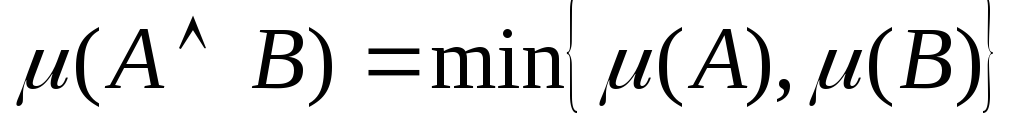 ;
;дизъюнкция двух нечетких высказываний
 и
и  обозначается как
обозначается как 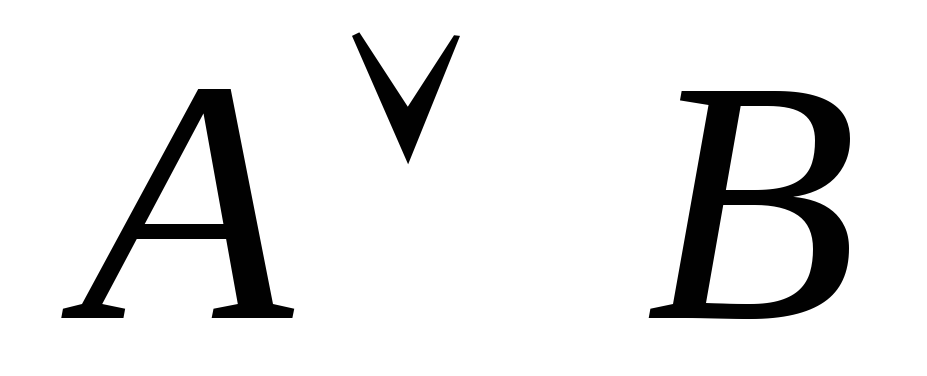 и имеет степень истинности
и имеет степень истинности 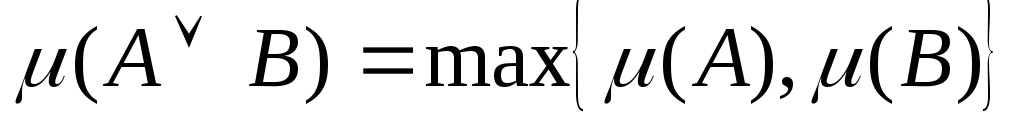 ;
;отрицание нечеткого высказывания
 - есть высказывание
- есть высказывание  степенью истинности
степенью истинности 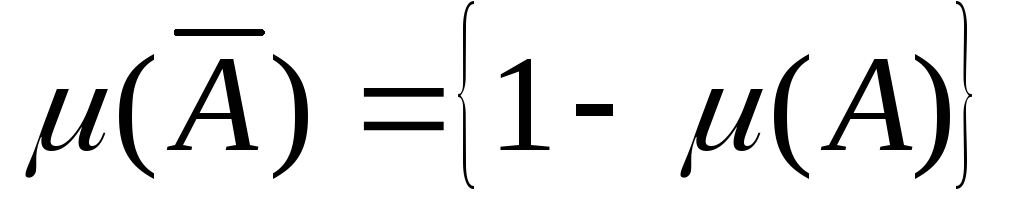 ;
;импликация двух нечетких высказываний есть нечеткое высказывание
 со степенью истинности
со степенью истинности 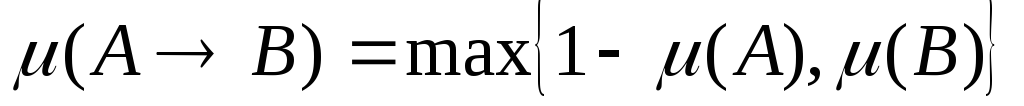 ;
;
Истинность импликации не меньше чем степень ложности ее посылки или степени истинности ее следствия.
Пример.
Пусть нечеткое высказывание ![]() имеет степень истинности
имеет степень истинности ![]() ,
а нечеткое высказывание
,
а нечеткое высказывание ![]() имеет степень истинности
имеет степень истинности ![]() .
Импликация этих высказываний
.
Импликация этих высказываний ![]() будет иметь степень истинности
будет иметь степень истинности
![]()
Эквивалентность двух нечетких высказываний
 и
и  есть нечеткое высказывание
есть нечеткое высказывание  ,
степень истинности, которого определяется,
как
,
степень истинности, которого определяется,
как
![]()
Из
определения эквивалентности следует,
что истинность эквивалентности совпадает
с менее истинной из импликаций ![]() и
и ![]() .
.
Определение.
Два
нечетких высказывания ![]() и
и ![]() называются нечетко близкими, если
степень истинности их эквивалентности
называются нечетко близкими, если
степень истинности их эквивалентности
![]() больше или равна 0.5. В последнем случае
высказывания
больше или равна 0.5. В последнем случае
высказывания ![]() и
и ![]() называют взаимно нечетко индифферентными.
называют взаимно нечетко индифферентными.
Порядок выполнения операций над высказываниями таков: скобки, отрицание, конъюнкция, дизъюнкция, импликация и эквивалентность.
Пример. Вычислить степень истинности составного нечеткого высказывания
![]() ,
если
,
если ![]() ,
,
![]() и
и ![]()