
- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
4 Нечеткие числа
4.1 Понятие нечеткого числа
Нечеткие
числа
– это нечеткие переменные на числовой
оси, другими словами, нечеткое число
определяется как нечеткое множество ![]() на множестве действительных чисел
на множестве действительных чисел ![]() с функцией принадлежности
с функцией принадлежности ![]() ,
где
,
где ![]() .
.
Нечеткое
число называется нормальным,
если ![]() и выпуклым,
если для любых
и выпуклым,
если для любых![]() выполняется
выполняется
![]() .
.
Множество
![]() - уровня нечеткого числа
- уровня нечеткого числа ![]() определяется как четкое множество
определяется как четкое множество
![]() .
.
Подмножество
![]() называется носителем нечеткого числа
называется носителем нечеткого числа
![]() ,
если
,
если
![]() .
.
Нечеткое
число унимодально,
если условие ![]() справедливо только для одной точки
действительной оси.
справедливо только для одной точки
действительной оси.
Выпуклое
нечеткое число называется нечетким
нулем,
если ![]() .
.
Нечеткое
число положительно,
если ![]()
![]() и отрицательно,
если
и отрицательно,
если ![]()
![]() .
.
4.2 Операции над нечеткими числами
Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом:
-
сложение
![]() ,
,
![]() ;
;
-
вычитание
![]() ,
,
![]() ;
;
-
умножение
![]() ,
,
![]() ;
;
-
деление
![]() ,
,
![]() .
.
Использовать
определенные таким образом алгебраические
операции над нечеткими числами
нецелесообразно, ввиду большого объема
вычислений. Поэтому часто используют
представление нечетких чисел в ![]() -
форме, что соответствует описанию левой
(left)
и правой (right)
частей функции принадлежности.
-
форме, что соответствует описанию левой
(left)
и правой (right)
частей функции принадлежности.
Нечеткое
число в ![]() -
форме имеет представление
-
форме имеет представление
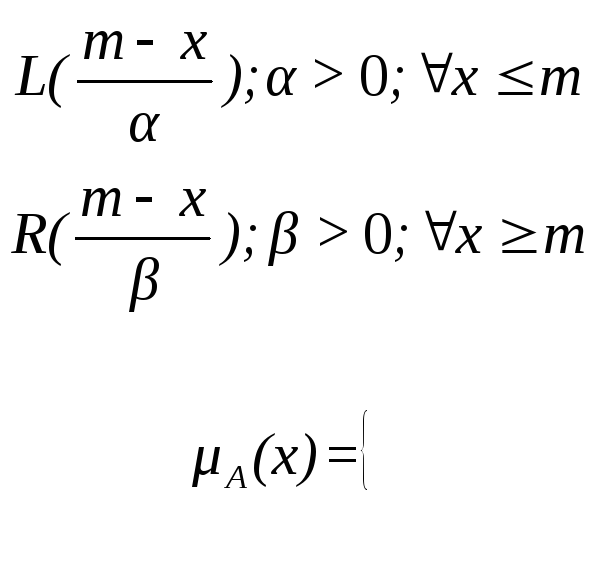
где
![]() и
и ![]() - функции, обладают свойствами:
- функции, обладают свойствами:
![]() ,
,
![]() .
.
Функция
![]() монотонно убывает на промежутке
монотонно убывает на промежутке ![]() .
Здесь
.
Здесь ![]() - среднее значение нечеткого числа,
- среднее значение нечеткого числа, ![]() - отклонение от среднего значения слева,
- отклонение от среднего значения слева,
![]() - отклонение справа. Если
- отклонение справа. Если ![]() =
=![]() =0,
то нечеткое число
=0,
то нечеткое число ![]() переходит в четкое число
переходит в четкое число ![]() .
.
Таким
образом, нечеткое число в ![]() -
форме можно представить в виде тройки
чисел
-
форме можно представить в виде тройки
чисел ![]() .
Тогда арифметические операции над
нечеткими числами можно определить
через операции над соответствующими
им тройками:
.
Тогда арифметические операции над
нечеткими числами можно определить
через операции над соответствующими
им тройками:
- сложение
![]()
- вычитание
![]()
- умножение
![]()
На
практике ![]() -
представление упрощается за счет
применения линейных функций, что приводит
к треугольным нечетким числам, которые
функцию принадлежности следующего вида
-
представление упрощается за счет
применения линейных функций, что приводит
к треугольным нечетким числам, которые
функцию принадлежности следующего вида
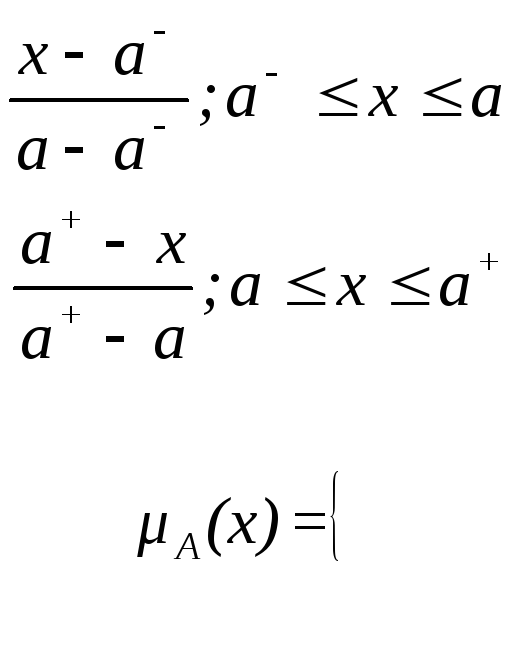 .
.
Кроме того, получили распространение трапециевидные формы функций принадлежности, которые имеют вид
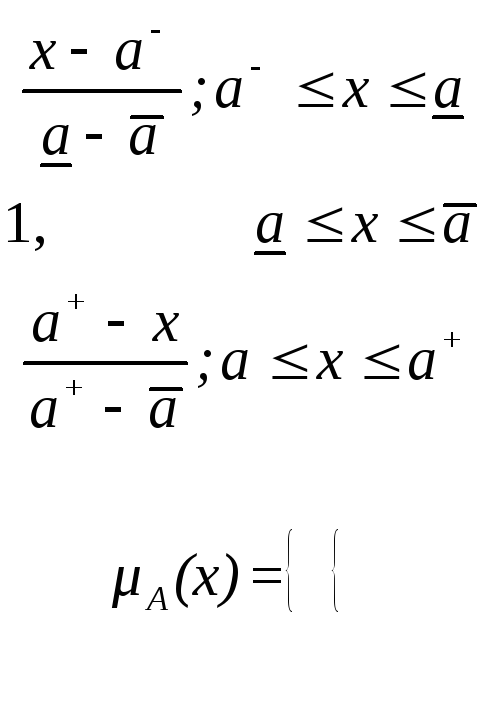 .
.
Решение задач математического моделирования сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над различного рода лингвистическими и другими нечеткими переменными. Для удобства выполнения операций, а также для ввода-вывода и хранения данных, желательно работать с функциями принадлежности стандартного типа.
К сожалению, даже при сведении нечетких чисел до понятия треугольных чисел, остаются нерешенными проблемы противоположного и обратного элементов и свойство дистрибутивности. Еще один существенный недостаток такого подхода. Размытость произведения зависит не только от размытости сомножителей, но и от того, какое место данные нечеткие числа занимают на числовой оси. Например, пусть
А=(1, 2, 3), В=(2, 3, 4), тогда АВ=(2, 6, 12)
и С=(99, 100, 101), Е=(100, 101, 102),
тогда СЕ=(9 900, 10 100, 10 302).
Из этого примера следует, что СЕ более размыто, чем АВ.
Нечеткие
множества, которые приходится применять
в большинстве задач, являются, как
правило, унимодальными и нормальными.
Одним из возможных методов аппроксимации
унимодальных нечетких множеств является
аппроксимация с помощью ![]() -
представлении.
-
представлении.
