
- •2008 Содержание
- •5.8 Нечеткие высказывания и нечеткие выводы… 112
- •6. Построение нечетких систем в диалоговом режиме с помощью Fuzzy Logic Toolbox ……….130
- •1 Обоснование теории нечетких множеств
- •1.1 Введение
- •1.2 Анализ видов неопределенности информации, характерных для процесса управления сложными системами
- •1.3 Человеко-машинные системы
- •1.4 Нечеткие системы
- •1.5 Возможности применения теории нечетких множеств и интервального анализа для описания различных видов неопределенности
- •2. Теория нечетких множеств
- •2.1. Четкие множества
- •2.2 Операции над четкими множествами
- •2.3 Декартово произведение множеств
- •3. Нечеткие множества
- •3.1 Понятие нечеткого множества
- •3.2 Некоторые характеристики нечетких множеств
- •3.3 Нечеткая и лингвистическая переменные
- •3.4 О методах построения функций принадлежности нечетких множеств
- •3.5 Операции над нечеткими множествами
- •4 Нечеткие числа
- •4.1 Понятие нечеткого числа
- •4.2 Операции над нечеткими числами
- •4.3 Нечеткие отношения
- •4.4 Свойства нечетких отношений
- •5 Основы математической логики
- •5.1 Алгебра высказываний
- •5.2 Булевы функции
- •5.3 Логика предикатов
- •5.4 Равносильные формулы логики предикатов
- •1) И ;
- •2) И ;
- •3) И ;
- •4) И .
- •5.5 Нечеткая логика
- •5.6 Нечеткие логические формулы и их свойства
- •5.7 Нечеткие предикаты и кванторы
- •5.8 Нечеткие высказывания и нечеткие выводы
- •5.9 Промышленные применения
- •6. Построение нечетких систем в
- •Диалоговом режиме с помощью
- •Fuzzy Logic Toolbox
- •1. Алгебра высказываний.
5.6 Нечеткие логические формулы и их свойства
Определение.
Нечеткая высказывательная переменная
![]() - это нечеткое высказывание, степень
истинности которого может принимать
значения из интервала [0,1].
- это нечеткое высказывание, степень
истинности которого может принимать
значения из интервала [0,1].
Определение.
Нечеткой логической формулой ![]() называется:
называется:
а) любая нечеткая высказывательная переменная или константа из [0,1];
б)
выражение ![]() ,
полученное из нечетких логических
формул
,
полученное из нечетких логических
формул ![]() и
и ![]() применением к ним любого конечного
числа логических операций.
применением к ним любого конечного
числа логических операций.
В частности, составные нечеткие высказывания также являются логическими формулами, если образующие их нечеткие высказывания рассматривать как нечеткие высказывательные переменные.
Определение.
Степень
равносильности формул ![]() и
и ![]() обозначается, как
обозначается, как ![]() и определяется следующим образом
и определяется следующим образом
![]() =
=![]()
![]() ).
).
Если
степень равносильности нечетких
логических формул ![]() и
и ![]() на всех определенных наборах степеней
истинности высказывательных переменных
больше или равно 0.5, то такие формулы
называются нечетко близкими на этих
наборах и обозначаются как
на всех определенных наборах степеней
истинности высказывательных переменных
больше или равно 0.5, то такие формулы
называются нечетко близкими на этих
наборах и обозначаются как ![]() .
Если
.
Если ![]() ,
то формулы не являются нечетко близкими.
,
то формулы не являются нечетко близкими.
Отметим,
что при ![]() формулы одновременно являются и не
являются нечетко близкими и их называют
индифферентными. Равносильность четких
логических формул является частным
случаем нечеткой близости.
формулы одновременно являются и не
являются нечетко близкими и их называют
индифферентными. Равносильность четких
логических формул является частным
случаем нечеткой близости.
Пример. Определить степень равносильности формул:
![]() и
и
![]() ,
,
где
![]() принимает степени истинности из набора
дискретных значений {0.8,0.6,0.7}, а
принимает степени истинности из набора
дискретных значений {0.8,0.6,0.7}, а ![]() -
из {0.3,0.4}.
-
из {0.3,0.4}.
Выбирая
все возможные наборы степеней истинности
![]() и
и ![]() ,
получим
,
получим
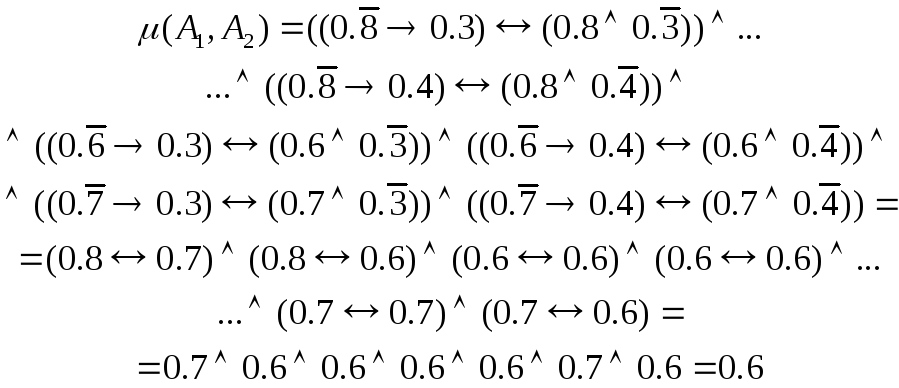
Отсюда
следует, что формулы нечетко близки![]() .
.
Проверить
самостоятельно будут ли эти формулы
нечетко близкими, если ![]() принимает степени истинности из набора
дискретных значений {0.2,0.4}, а
принимает степени истинности из набора
дискретных значений {0.2,0.4}, а ![]() - из {0.6,0.7,0.8}.
- из {0.6,0.7,0.8}.
Определение.
Если
при всех определенных значениях степеней
истинности нечетких переменных ![]() значение степени истинности логической
формулы
значение степени истинности логической
формулы ![]() больше или равно 0.5, то формула является
нечетко истинной на данном наборе
переменных и обозначается через
больше или равно 0.5, то формула является
нечетко истинной на данном наборе
переменных и обозначается через ![]() .
Если значение степени истинности меньше
или равно 0.5, то логическая формула
называется нечетко ложной и обозначается
.
Если значение степени истинности меньше
или равно 0.5, то логическая формула
называется нечетко ложной и обозначается
![]() .
.
Пусть
![]() нечетко истинные и нечетко ложные
формулы на одних и тех же наборах
переменных, тогда справедливы следующие
соотношения:
нечетко истинные и нечетко ложные
формулы на одних и тех же наборах
переменных, тогда справедливы следующие
соотношения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если
![]() произвольные ложные формулы, то
справедливы соотношения:
произвольные ложные формулы, то
справедливы соотношения:
![]() ,
,
![]() ,
,
где
![]() определены на одних и тех же наборах
переменных.
определены на одних и тех же наборах
переменных.
Пример. Простейшие примеры нечетко истинных и нечетко ложных формул
![]() и
и
![]()
Это следует из определения операций отрицания, конъюнкции и дизъюнкции.
Если
одна нечеткая логическая формула имеет
представление ![]() ,
а другая -
,
а другая - ![]() ,
где
,
где ![]() нечеткие формулы от переменных
нечеткие формулы от переменных ![]() ,
то можно утверждать, что такие формулы
нечетко близкие
,
то можно утверждать, что такие формулы
нечетко близкие ![]() .
.
Доказательство:
![]()
продолжить доказательство.
Запишем
соотношения, справедливые для любых
наборов значений истинности нечетких
переменных. Пусть ![]() - нечеткие логические формулы, тогда
имеет место
- нечеткие логические формулы, тогда
имеет место
1.
![]() ,
,
2.
![]() ,
,
3.
![]() ,
,
![]() ,
,
4.
![]() ,
,
![]() ,
,
5.
![]() ,
,
![]() ,
,
6.
![]() ,
,
![]() ,
,
7.
![]() ,
,
![]() ,
,
8.
![]() ,
,
9.
![]() ,
,
10.
![]() ,
,
11.
![]() ,
,
12.
![]() ,
,
![]() ,
,
13.
![]() ,
,
14.
![]() ,
,
15.
![]() ,
,
16.
![]() .
.
Пусть
![]() - константы и
- константы и ![]() ,
тогда имеют место следующие соотношения:
,
тогда имеют место следующие соотношения:
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
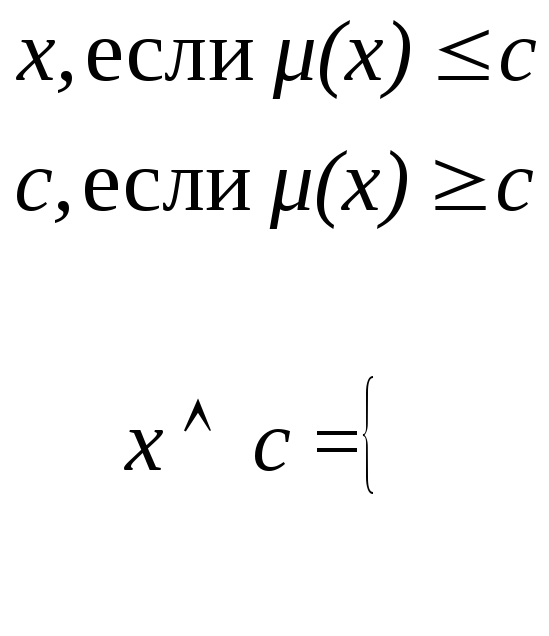 ,
,
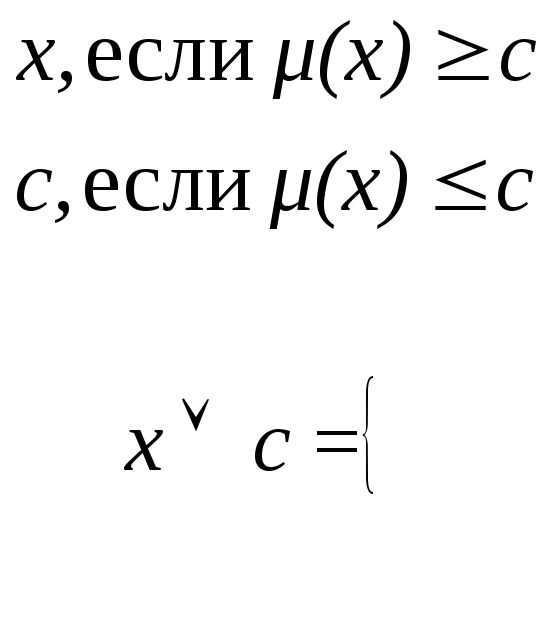 .
.
Для
доказательства каждого из приведенных
выражений необходимо показать, что
степень равносильности ![]() формул больше или равно 0.5. Это возможно
тогда, когда формулы
формул больше или равно 0.5. Это возможно
тогда, когда формулы ![]() принимают одни и те же значения степени
истинности на одинаковых наборах
переменных, либо имеют степень истинности
одновременно меньшую или равную 0.5 или
большую или равную 0.5.
принимают одни и те же значения степени
истинности на одинаковых наборах
переменных, либо имеют степень истинности
одновременно меньшую или равную 0.5 или
большую или равную 0.5.
В
качестве примера докажем формулу (6) ![]() .
Для доказательства обозначим
.
Для доказательства обозначим ![]() и
и ![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Пусть
на всех наборах одновременно выполняется
![]() ,
тогда
,
тогда ![]() ,
а
,
а ![]() .
.
Степень истинности определится как
![]()
Показать
истинность этой формулы при ![]() .
.
В
четкой логике логические операции могут
быть заданы таблицами истинности. В
нечеткой логике количество возможных
значений истинности может быть
бесконечным, поэтому представление в
табличном виде логических операций
невозможно. Однако в табличном виде
можно представить нечеткие логические
операции для ограниченного количества
истинностных значений, например, для
терм-множества {«истинно», «очень
истинно», «не истинно», «более-менее
ложно», «ложно»}. Для трехзначной логике
с нечеткими значениями истинности: ![]() -
«истинно»,
-
«истинно», ![]() - «ложно»,
- «ложно», ![]() - «неизвестно» Л. Заде предложил такие
лингвистические таблицы истинности,
которые легко получить, исходя из выше
приведенных формул.
- «неизвестно» Л. Заде предложил такие
лингвистические таблицы истинности,
которые легко получить, исходя из выше
приведенных формул.
Таблица 17
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя правила выполнения нечетких логических операций, определенных выше, можно расширить таблицу истинности для большого числа термов. Как это сделать рассмотрим на следующем примере.
Пример. Заданы следующие нечеткие истинностные значения:
Истинно = 0/0+0/0.2+0.25/0.4+0.5/0.6+0.9/0.8+1/1;
Более – менее истинно
= 0/0+0/0.2+0.5/0.4+0.7/0.6+0.95/0.8+1/1;
Почти истинно
= 0/0+0.05/0.2+0.4/0.4+0.7/0.6+1/0.8+0.8/1.
Применяя правила выполнения нечетких логических операций, найдем значение выражения «почти истинно ИЛИ истинно»:
Почти
истинно ![]() истинно
истинно
= 0/0+0.05/0.2+0.4/0.4+1/0.8+1/1.
Из сравнения полученного нечеткого множества с нечетким множеством «более – менее истинно», видно, что они почти равны. Значит
Почти
истинно ![]() истинно
истинно
![]() более
– менее истин.
более
– менее истин.
В результате выполнения логических операций часто получаются нечеткие множества, которые не эквивалентны ни одному из ранее введенных нечетких значений истинности. В этом случае необходимо среди нечетких значений истинности найти такое, которое соответствует результату выполнения логической операции в максимальной степени. Другими словами, необходимо провести так называемую лингвистическую аппроксимацию, которая может рассматриваться как аналог аппроксимации эмпирического статистического распределения стандартными функциями распределения случайных величин. В качестве примера рассмотрим предложенные Балдвином лингвистические таблицы истинности для нечетких значений истинности
Таблица 18
-

ложно
ложно
истинно
ложно
истинно
истинно
неопределенно
ложно
неопределенно
истинно
неопределенно
неопределенно
истинно
очень истинно
истинно
более-менее истинно
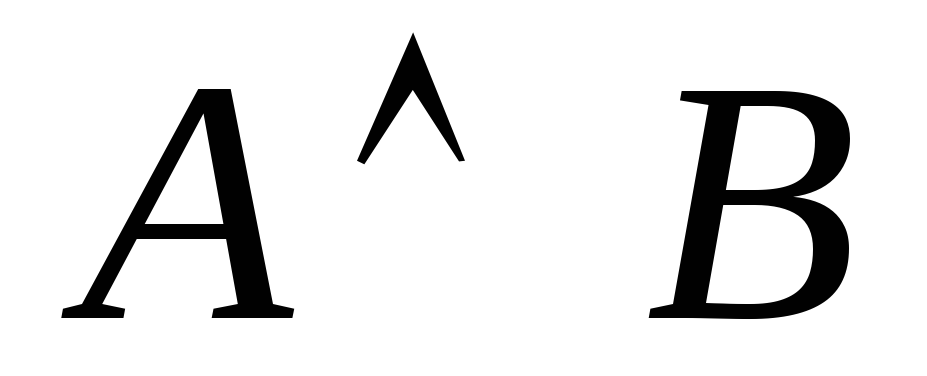
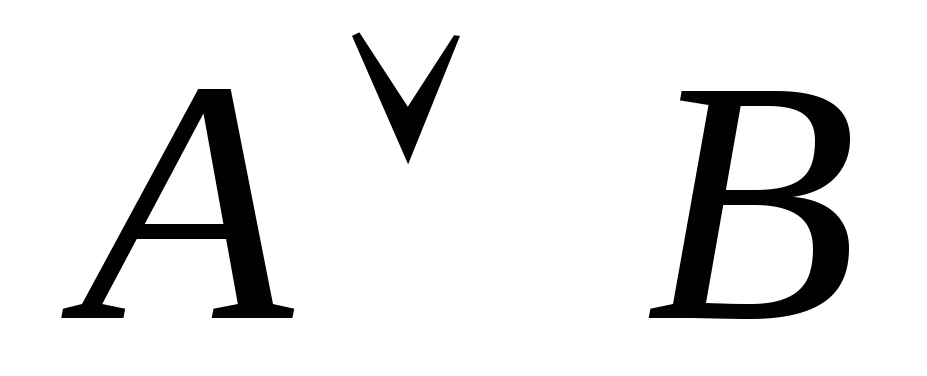
ложно
ложно
ложно
истинно
истинно
истинно
ложно
неопределенно
неопределенно
истинно
неопределенно
неопределенно
истинно
очень истинно
более-менее истинно
истинно
Вначале
рассмотрим расширения НЕ, И, ИЛИ до
нечетких операций. Эти расширения
называются соответственно нечетким
отрицанием называются ![]() -нормой
и
-нормой
и ![]() -
нормой. В нечетком мире число состояний
неограниченно велико, поэтому невозможно
описать эти операции с помощью таблицы
истинности, как в случае двузначной
логики. Поясним эти операции, используя
функции и несколько аксиом.
-
нормой. В нечетком мире число состояний
неограниченно велико, поэтому невозможно
описать эти операции с помощью таблицы
истинности, как в случае двузначной
логики. Поясним эти операции, используя
функции и несколько аксиом.
