
- •2. Нелинейные системы автоматического управления
- •2.1 Общие сведения о нелинейных системах
- •2.2. Математические модели замкнутых нелинейных систем автоматического управления
- •2.3. Исследование нелинейных систем методом фазовой плоскости
- •2.3.1. Основные понятия
- •2.3.2. Классификация фазовых портретов
- •2.3.3. Построение фазовых траекторий
- •2.3.4. Скользящие режимы в нелинейных системах
- •2.3.5. Система с переменной структурой
- •2.4. Метод припасовывания
- •2.5. Метод точечного преобразования
- •2.6.Метод гармонической линеаризации
- •2.6.1. Исходные положения метода гармонической линеаризации
- •2.6.2. Вычисление коэффициентов гармонической линеаризации
- •2.6.3. Алгебраический метод определения симметричных колебаний
- •2.6.4. Частотный метод определения симметричных колебаний
- •2.6.5. Вынужденные колебания в нелинейных системах
- •2.7.Устойчивость процессов в нелинейных системах
- •2.7.1.Основные понятия и определения
- •2.7.2.Теоремы Ляпунова
- •2.7.3. Абсолютная устойчивость
- •2.8. Коррекция нелинейных систем
- •2.8.1. Коррекция нелинейной системы с помощью обратной связи
- •2.8.2. Коррекция нелинейной системы с помощью вибрационного сглаживания
- •3. Случайные процессы в системах автоматического управления
- •3.1. Случайные процессы и их характеристики
- •3.2. Прохождение случайных сигналов через линейную непрерывную систему автоматического управления
- •3.3. Расчёт точности системы при случайных воздействиях
- •3.4. Особенности синтеза систем автоматического управления
- •3.5. Случайные процессы в импульсных системах
- •3.6. Случайные процессы в нелинейных системах
- •4. Элементы современной теории автоматического управления
- •4.1. Оптимальное управление
- •4.2 Интеллектуальные сау
- •4.2.1. Экспертные информационные системы
- •4.2.2. Нейросетевые сау
- •4.2.3. Сау с ассоциативной памятью
- •4.2.4. Системы управления с нечёткой логикой
- •Литература
2.7.2.Теоремы Ляпунова
Кроме определений Ляпуновым были разработаны два метода анализа устойчивости решений дифференциальных уравнений.
Суть первого метода
заключается в замене нелинейной системы
(2.70) линейной (линеаризованной) путем
разложения правых частей уравнений
(2.70) в ряды Тейлора относительно начала
координат
![]() и отбрасывания всех нелинейных членов.
В результате получаются линейные
уравнения (уравнения первого приближения)
и отбрасывания всех нелинейных членов.
В результате получаются линейные
уравнения (уравнения первого приближения)
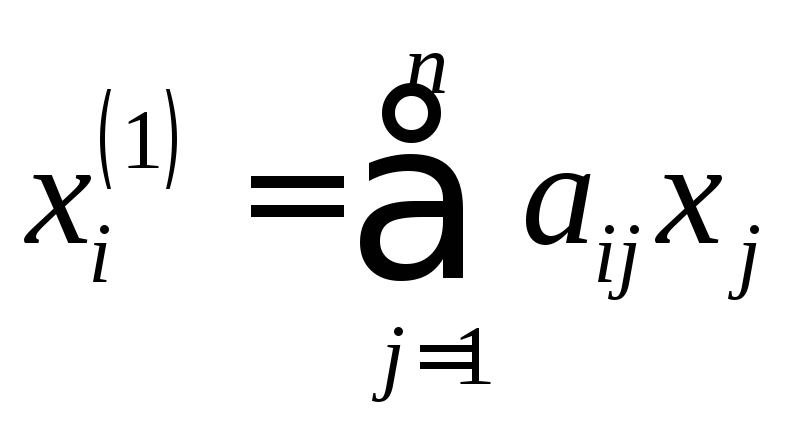 ,
,![]() , (2.71)
, (2.71)
где
![]() − постоянные коэффициенты.
− постоянные коэффициенты.
Ляпуновым доказана следующая основная теорема первого метода, которую приведем в упрощенной форме: если линейная система (2.71) асимптотически устойчива, то положение равновесия нелинейной системы (2.70) будет асимптотически устойчивым в малом, если система (2.71) неустойчива, то положение равновесия (2.70) будет неустойчивым.
По первому методу, исключая так называемые критические случаи, задача анализа устойчивости нелинейной системы сведена к более простой задаче анализа линейной системы. Первый метод Ляпунова не позволяет исследовать устойчивость в большом, целом или абсолютную устойчивость. Для этих целей Ляпуновым был разработан второй метод или прямой метод анализа устойчивости.
Введем в рассмотрение
непрерывную функцию
![]()
![]() переменных, такую, что
переменных, такую, что![]() при
при![]() ,
,![]() ,
т.е. обращающуюся обязательно в ноль в
начале координат.
,
т.е. обращающуюся обязательно в ноль в
начале координат.
Если в некоторой
области переменных
![]() функция
функция![]() или
или![]() ,
то ее называютзнакоопределенной:
соответствен положительно
определенной
или отрицательно
определенной.
Если функция
,
то ее называютзнакоопределенной:
соответствен положительно
определенной
или отрицательно
определенной.
Если функция
![]() сохраняет свой знак, но может обращаться
в ноль не только в начале координат, то
ее называютзнакопостоянной
(положительной
или отрицательной).
Такие функции в дальнейшем будем называть
функциями
Ляпунова.
Примеры функций:
сохраняет свой знак, но может обращаться
в ноль не только в начале координат, то
ее называютзнакопостоянной
(положительной
или отрицательной).
Такие функции в дальнейшем будем называть
функциями
Ляпунова.
Примеры функций:
![]() − положительно
определенная;
− положительно
определенная;![]() − отрицательно
определенная;
− отрицательно
определенная;
![]() − знакопостоянная
функция (положительная).
− знакопостоянная
функция (положительная).
Наконец, функция
![]() называетсязнакопеременной,
если в рассматриваемой области она
меняет свой знак. Например,
называетсязнакопеременной,
если в рассматриваемой области она
меняет свой знак. Например,
![]() .
.
Приведем три основные теоремы Ляпунова второго метода.
1. Если для
системы уравнений (2.70) существует
знакоопределенная функция
![]() ,
производная которой
,
производная которой![]() является знакопостоянной противоположного
знака, то решение
является знакопостоянной противоположного
знака, то решение![]() устойчиво.
устойчиво.
2. Если в предыдущем
случае производная
![]() будет знакоопределенной, но противоположного
знака, то решение
будет знакоопределенной, но противоположного
знака, то решение![]() будет устойчивым асимптотическим.
будет устойчивым асимптотическим.
3. Если для
системы уравнений (2.70) существует функция
![]() ,
производная которой
,
производная которой![]() является знакоопределенной функцией,
причем в любой сколь угодно малой
окрестности начала координат, имеется
область, в которой знаки
является знакоопределенной функцией,
причем в любой сколь угодно малой
окрестности начала координат, имеется
область, в которой знаки![]() и
и![]() совпадают, то решение
совпадают, то решение![]() системы (2.70) неустойчиво.
системы (2.70) неустойчиво.
Отметим, что
приведенные в теоремах условия являются
только лишь достаточными и эффективность
их будет зависеть от выбранной функции
Ляпунова
![]() .
Не существует в общем случае методик
выбора функций Ляпунова, дающих
необходимые и достаточные условия.
.
Не существует в общем случае методик
выбора функций Ляпунова, дающих
необходимые и достаточные условия.
Довольно часто в качестве функций Ляпунова используют квадратичные формы, для которых, используя известные критерии, можно сравнительно легко определять их знак.
2.7.3. Абсолютная устойчивость
Рассмотрим понятие абсолютной устойчивости применительно к структуре нелинейной системы рис. 2.2.
Уравнения,
описывающие поведение системы при
![]() имеют в соответствии с [8] вид
имеют в соответствии с [8] вид
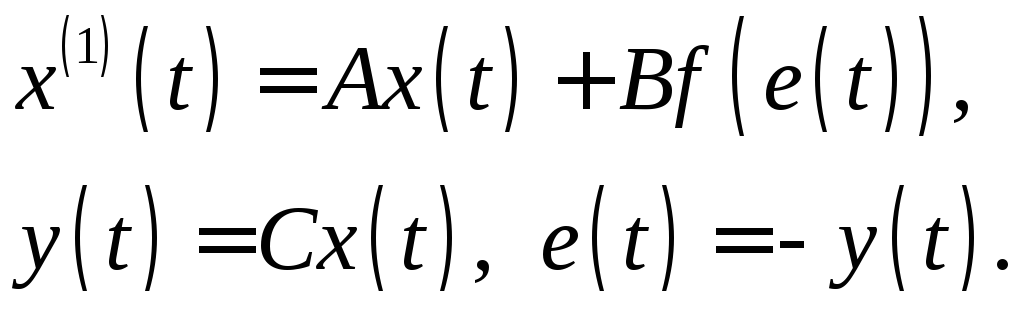 (2.72)
(2.72)
Будем полагать,
что
![]() ,
тогда уравнения имеют тривиальное
решение
,
тогда уравнения имеют тривиальное
решение![]() ,
,![]() ,
,![]() ,
т.е. в системе существует положение
равновесия, устойчивость которого будем
исследовать.
,
т.е. в системе существует положение
равновесия, устойчивость которого будем
исследовать.
Если положение
равновесия системы (2.72) асимптотически
устойчиво в целом при любом виде функции
![]() из заданного класса, то САУ называетсяабсолютно
устойчивой
в этом классе.
из заданного класса, то САУ называетсяабсолютно
устойчивой
в этом классе.
Будем рассматривать
класс функций
![]() ,
удовлетворяющих секторным ограничениям,
т.е. с характеристикой
,
удовлетворяющих секторным ограничениям,
т.е. с характеристикой![]() ,
построенной на плоскости
,
построенной на плоскости![]() ,
которая полностью укладывается в угловом
секторе, образованном двумя прямыми
,
которая полностью укладывается в угловом
секторе, образованном двумя прямыми![]() и
и![]() ,
,![]() .
.
Итак, рассматривается класс нелинейных функций, удовлетворяющих условиям
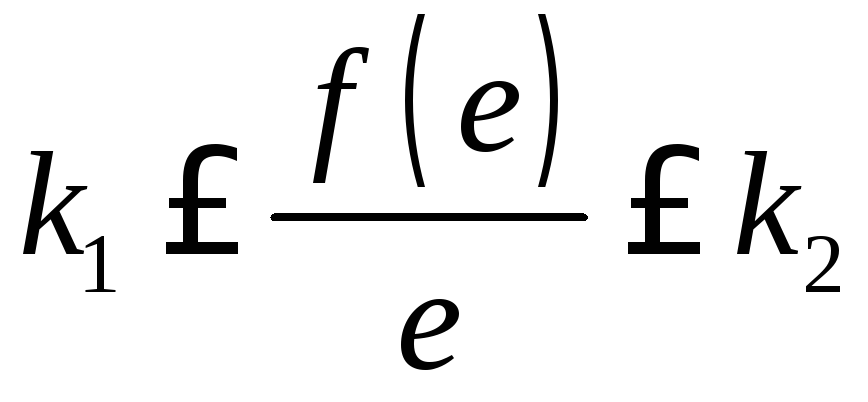 для
для![]() ,
,![]() . (2.73)
. (2.73)
При этом вид функции
![]() неизвестен, а нелинейность будет
относиться к классу
неизвестен, а нелинейность будет
относиться к классу![]() .
Возможны также дополнительные ограничения,
например, функция
.
Возможны также дополнительные ограничения,
например, функция![]() должна быть непрерывной или другие.
должна быть непрерывной или другие.
Из класса (2.73)
выделяют два подкласса:
![]() и
и![]() ,
,![]() .
.
Анализ абсолютной устойчивости возможен с помощью функций Ляпунова, а также частотных критериев абсолютной устойчивости. Рассмотрим последние как наиболее практичные.
Круговой критерий устойчивости.
Для нелинейностей
из класса
![]() достаточным условием абсолютной
устойчивости является выполнение
неравенства
достаточным условием абсолютной
устойчивости является выполнение
неравенства
![]() , (2.74)
, (2.74)
где
![]() ,
,![]() ,
,![]() − АФЧХ
линейной части системы (рис. 2.2).
− АФЧХ
линейной части системы (рис. 2.2).
Неравенство (2.74) определяет область на комплексной плоскости, в которой должна лежать АФЧХ линейной части системы, чтобы нелинейная система была абсолютно устойчива.
Заменяя
в (2.74) знак неравенства на знак равенства,
получим границу этой области. Это будет
уравнение окружности с центром на
вещественной оси в точке
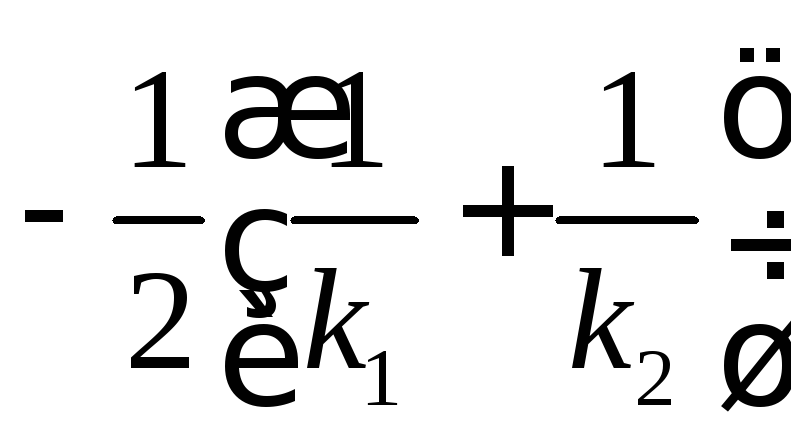 и проходящей через точки
и проходящей через точки![]() и
и![]() на оси
на оси![]() .
Неравенство (2.74) требует, чтобы АФЧХ при
всех
.
Неравенство (2.74) требует, чтобы АФЧХ при
всех![]() располагалась вне круга, ограниченного
этой окружностью. На рис. 2.20 приведены
запретные области (заштрихованные) для
характеристики
располагалась вне круга, ограниченного
этой окружностью. На рис. 2.20 приведены
запретные области (заштрихованные) для
характеристики![]() и характеристики
и характеристики![]() .
.

Рис. 2.20
В [4] даются более
подробные случаи для разных классов
![]() .
.
Вторым распространенным
частотным критерием является критерий
В.М. Попова.
Рассмотрим его формулировку для класса
нелинейных характеристик
![]() :
система будет абсолютно устойчивой для
нелинейностей из класса
:
система будет абсолютно устойчивой для
нелинейностей из класса![]() ,
если через точку
,
если через точку![]() можно провести прямую так, что она не
пересечет модифицированную частотную
характеристику (последняя лежит справа
от прямой).
можно провести прямую так, что она не
пересечет модифицированную частотную
характеристику (последняя лежит справа
от прямой).
В этом критерии
под модифицированной частотной
характеристикой понимается характеристика
![]() ,
где
,
где![]() ,
,![]() .
.
Рис. 2.21, а
удовлетворяет критерию абсолютно
устойчивой системы, а рис. 2.21, б
при заданном
![]() не удовлетворяет этому критерию.
не удовлетворяет этому критерию.

Рис. 2.21
В заключение отметим, что все критерии абсолютной устойчивости, в том числе частотные, дают только лишь достаточные условия абсолютной устойчивости.
