
- •2. Нелинейные системы автоматического управления
- •2.1 Общие сведения о нелинейных системах
- •2.2. Математические модели замкнутых нелинейных систем автоматического управления
- •2.3. Исследование нелинейных систем методом фазовой плоскости
- •2.3.1. Основные понятия
- •2.3.2. Классификация фазовых портретов
- •2.3.3. Построение фазовых траекторий
- •2.3.4. Скользящие режимы в нелинейных системах
- •2.3.5. Система с переменной структурой
- •2.4. Метод припасовывания
- •2.5. Метод точечного преобразования
- •2.6.Метод гармонической линеаризации
- •2.6.1. Исходные положения метода гармонической линеаризации
- •2.6.2. Вычисление коэффициентов гармонической линеаризации
- •2.6.3. Алгебраический метод определения симметричных колебаний
- •2.6.4. Частотный метод определения симметричных колебаний
- •2.6.5. Вынужденные колебания в нелинейных системах
- •2.7.Устойчивость процессов в нелинейных системах
- •2.7.1.Основные понятия и определения
- •2.7.2.Теоремы Ляпунова
- •2.7.3. Абсолютная устойчивость
- •2.8. Коррекция нелинейных систем
- •2.8.1. Коррекция нелинейной системы с помощью обратной связи
- •2.8.2. Коррекция нелинейной системы с помощью вибрационного сглаживания
- •3. Случайные процессы в системах автоматического управления
- •3.1. Случайные процессы и их характеристики
- •3.2. Прохождение случайных сигналов через линейную непрерывную систему автоматического управления
- •3.3. Расчёт точности системы при случайных воздействиях
- •3.4. Особенности синтеза систем автоматического управления
- •3.5. Случайные процессы в импульсных системах
- •3.6. Случайные процессы в нелинейных системах
- •4. Элементы современной теории автоматического управления
- •4.1. Оптимальное управление
- •4.2 Интеллектуальные сау
- •4.2.1. Экспертные информационные системы
- •4.2.2. Нейросетевые сау
- •4.2.3. Сау с ассоциативной памятью
- •4.2.4. Системы управления с нечёткой логикой
- •Литература
2.3.5. Система с переменной структурой
Структура нелинейной САУ изображена на рис. 2.9.

Рис. 2.9
На этом рисунке
нелинейным элементом является логическое
устройство, которое на основе измерения
сигнала
![]() управляет по определенному закону
ключом
управляет по определенному закону
ключом![]() ,
так что передаточная функция разомкнутой
системы может быть либо
,
так что передаточная функция разомкнутой
системы может быть либо![]() ,
либо
,
либо![]() ,
т.е. система в процессе работы меняет
свою структуру. При включении верхнего
звена уравнение замкнутой системы имеет
вид
,
т.е. система в процессе работы меняет
свою структуру. При включении верхнего
звена уравнение замкнутой системы имеет
вид
![]() , (2.27)
, (2.27)
а при включении нижнего звена
![]() . (2.28)
. (2.28)
Характеристическое
уравнение такой замкнутой системы будет
![]() и, если
и, если![]() ,
,![]() ,
имеет два комплексных корня, т.е. система
является нейтральной или находиться
на границе устойчивости. Такая система
является неработоспособной.
,
имеет два комплексных корня, т.е. система
является нейтральной или находиться
на границе устойчивости. Такая система
является неработоспособной.
Обозначим
![]() ,
,![]() ,
тогда уравнения для фазовых траекторий
будут
,
тогда уравнения для фазовых траекторий
будут
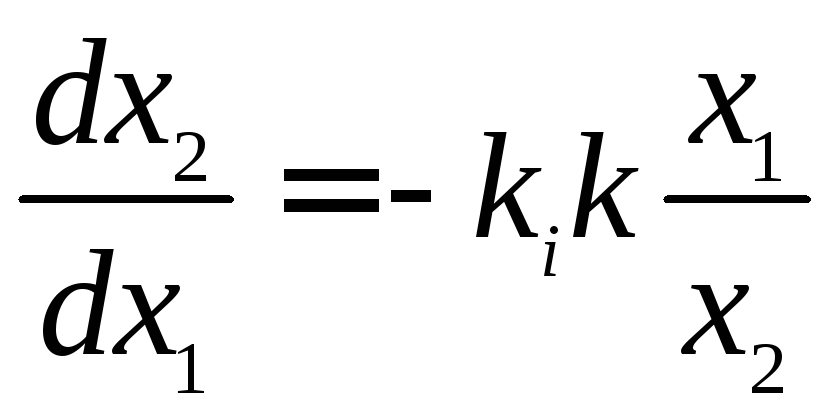 ,
,![]() . (2.29)
. (2.29)
Решая уравнения (2.29), получим на фазовой плоскости семейство эллипсов
![]() ,
,
где
![]() – произвольная постоянная.
– произвольная постоянная.
Путем подбора
![]() ,
,![]() сделаем одни эллипсы сжатыми вдоль оси
сделаем одни эллипсы сжатыми вдоль оси![]() ,
а другие вдоль оси
,
а другие вдоль оси![]() ,
как это изображено на рис. 2.10.
,
как это изображено на рис. 2.10.
Закон переключения
ключа выберем следующий: если
![]() ,
то имеем цепь с коэффициентом
,
то имеем цепь с коэффициентом![]() (рис. 2.10, а), если
(рис. 2.10, а), если![]() ,
то имеем цепь с коэффициентом
,
то имеем цепь с коэффициентом![]() (рис. 2.10, б). Линиями переключения
будут координатные оси фазовой плоскости
(рис. 2.10, б). Линиями переключения
будут координатные оси фазовой плоскости![]() ,
,![]() .
Итак, если изображающая точка находится,
например, в первом квадранте, то с
течением времени она движется вниз
вдоль эллипса до линии переключения
.
Итак, если изображающая точка находится,
например, в первом квадранте, то с
течением времени она движется вниз
вдоль эллипса до линии переключения![]() (рис. 2.10, а) и далее при
(рис. 2.10, а) и далее при![]() вдоль эллипса, сжатого относительно
оси
вдоль эллипса, сжатого относительно
оси![]() и т.д. Таким образом, с течением времени
изображающая точка будет стремиться к
началу координат.
и т.д. Таким образом, с течением времени
изображающая точка будет стремиться к
началу координат.

Рис. 2.10
В рассмотренном
случае процесс будет колебательным.
Однако возможно в такой системе
организовать скользящий режим. Пусть
в структуре рис. 2.9
![]() ,
тогда уравнения для фазовых траекторий
будут
,
тогда уравнения для фазовых траекторий
будут
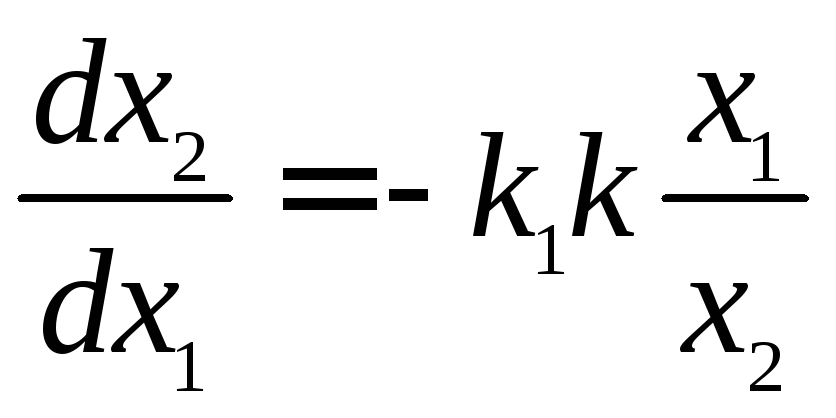 ,
,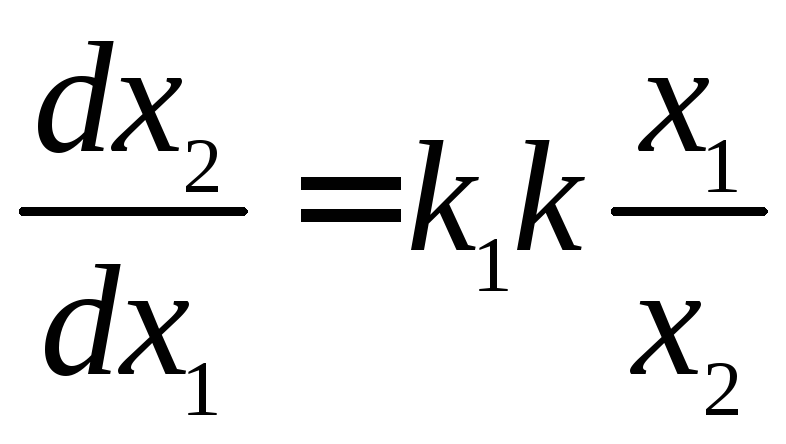 ,
,
первое из которых
при
![]() ,
,![]() описывает эллипсы, а второе при
описывает эллипсы, а второе при![]() ,
,![]() гиперболы на фазовой плоскости. Первый
контур соответствует, как и раньше,
нейтральной системе, а второй – неустойчивой
системе. Переключение организуем
следующим образом: если
гиперболы на фазовой плоскости. Первый
контур соответствует, как и раньше,
нейтральной системе, а второй – неустойчивой
системе. Переключение организуем
следующим образом: если![]() ,
работает верхняя цепь (коэффициент
,
работает верхняя цепь (коэффициент![]() ),
а если
),
а если![]() ,
работает нижняя цепь (коэффициент
,
работает нижняя цепь (коэффициент![]() ).
Таким образом, линиями переключения
будут
).
Таким образом, линиями переключения
будут![]() (ось ординат) и прямая
(ось ординат) и прямая![]() ,
где
,
где![]() – параметр, который можно выбирать.
Линия скольжения в данном случае не
ограничена конечным отрезком, а является
всей прямой
– параметр, который можно выбирать.
Линия скольжения в данном случае не
ограничена конечным отрезком, а является
всей прямой![]() .
Фазовый портрет изображен на рис. 2.11,
где волнистая линия – это линия
переключения.
.
Фазовый портрет изображен на рис. 2.11,
где волнистая линия – это линия
переключения.

Рис. 2.11
2.4. Метод припасовывания
Этот метод
применяется для случая, когда нелинейная
характеристика
![]() в САУ рис. 2.2 представляется в видекусочно-линейной,
т.е. на отдельных участках изменения
переменной
в САУ рис. 2.2 представляется в видекусочно-линейной,
т.е. на отдельных участках изменения
переменной
![]() нелинейная характеристика аппроксимируется
линейной зависимостью. Теоретически
этот подход можно применять для систем
любого порядка при вычислении как
свободных (
нелинейная характеристика аппроксимируется
линейной зависимостью. Теоретически
этот подход можно применять для систем
любого порядка при вычислении как
свободных (![]() ),
так и вынужденных процессов (
),
так и вынужденных процессов (![]() ).
).
Основная идея
подхода следующая. Диапазон изменения
переменной
![]() на входе нелинейности разбивается на
ряд интервалов, так что в
на входе нелинейности разбивается на
ряд интервалов, так что в![]() -ом
интервале
-ом
интервале![]() нелинейная функция
нелинейная функция![]() заменяется линейной
заменяется линейной![]() .
Тогда в
.
Тогда в![]() -ом
интервале уравнения (2.6), (2.8) или (2.9)
становятся линейными и теоретически
можно найти общее решение соответствующих
линейных дифференциальных уравнений
при заданном входе
-ом
интервале уравнения (2.6), (2.8) или (2.9)
становятся линейными и теоретически
можно найти общее решение соответствующих
линейных дифференциальных уравнений
при заданном входе![]() :
:
 (2.30)
(2.30)
где
![]() – произвольные постоянные.
– произвольные постоянные.
Задавая начальные
условия для частного (конкретного
решения)
![]() при условии
при условии![]() и полагая в (2.30)
и полагая в (2.30)![]() ,
находим произвольные постоянные и
соответствующие частные решения
,
находим произвольные постоянные и
соответствующие частные решения![]() ,
которые справедливы только при
,
которые справедливы только при![]() .
.
Далее находим
значение момента времени
![]() ,
при котором
,
при котором![]() ,
либо
,
либо![]() .
При
.
При![]() по выражениям (2.30) вычисляем конечные
значения решения и его производных
по выражениям (2.30) вычисляем конечные
значения решения и его производных![]() ,
которые принимаем за начальные значения
решения в следующем
,
которые принимаем за начальные значения
решения в следующем![]() или
или![]() интервалах. Далее процесс поинтервального
решения повторяется.
интервалах. Далее процесс поинтервального
решения повторяется.
Итак, для каждого
![]() -го
интервала изменения переменных системы
имеем свою линейную модель, которая
дает определенное решение, справедливое
только для
-го
интервала изменения переменных системы
имеем свою линейную модель, которая
дает определенное решение, справедливое
только для![]() -го
интервала. На границах интервалов, там,
где
-го
интервала. На границах интервалов, там,
где![]() ,
производится припасовывание (склеивание,
сшивание) решений: конечные значения
решений для
,
производится припасовывание (склеивание,
сшивание) решений: конечные значения
решений для![]() -го
интервала становятся начальными
значениями искомого решения для
следующего интервала. Отсюда и название
метода –метод
припасовывания решений.
Фактически он уже применялся для
нахождения решений дифференциальных
уравнений для фазовых траекторий в
пункте 2.3.3. Границы интервалов
-го
интервала становятся начальными
значениями искомого решения для
следующего интервала. Отсюда и название
метода –метод
припасовывания решений.
Фактически он уже применялся для
нахождения решений дифференциальных
уравнений для фазовых траекторий в
пункте 2.3.3. Границы интервалов
![]() являются линиями переключения.
являются линиями переключения.
Пример 2.3. Пусть
в нелинейной системе рис. 2.2
![]() ,
а нелинейность имеет вид рис. 2.4, а,
которая описывается уравнением
,
а нелинейность имеет вид рис. 2.4, а,
которая описывается уравнением
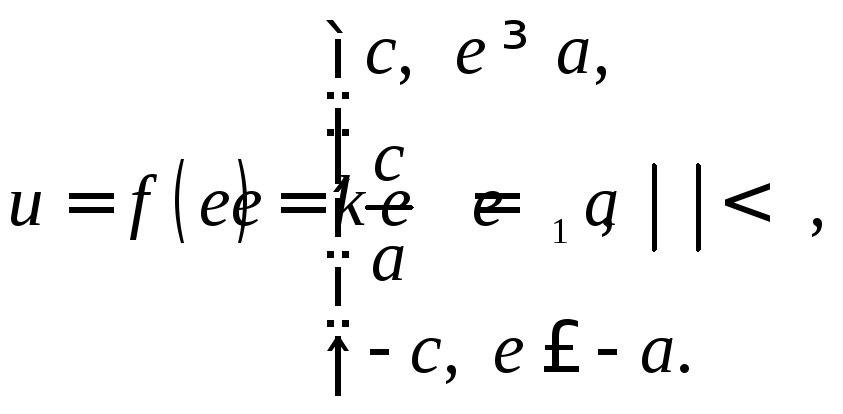 (2.31)
(2.31)
Исходная система нелинейных уравнений будет иметь вид
![]() . (2.32)
. (2.32)
Исследуем процессы
в системе при входном сигнале
![]() .
Тогда из (2.32) с учетом (2.31) получим три
модели системы для трех интервалов:
.
Тогда из (2.32) с учетом (2.31) получим три
модели системы для трех интервалов:
![]()
![]()
![]()
Общее решение в каждом случае будет иметь вид:
![]()
 (2.33)
(2.33)
![]()
Пусть
![]() ,
,![]() ,
тогда из первого уравнения (2.33) найдем
,
тогда из первого уравнения (2.33) найдем![]() и решение будет
и решение будет![]() .
Найдем момент времени
.
Найдем момент времени![]() ,
когда
,
когда![]() .
Это вытекает из решения уравнения
.
Это вытекает из решения уравнения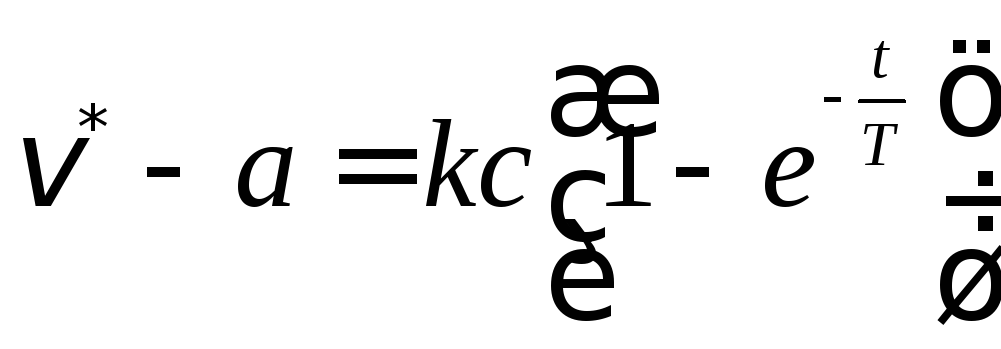 при условии
при условии![]() .
Момент
.
Момент![]() определится по формуле
определится по формуле
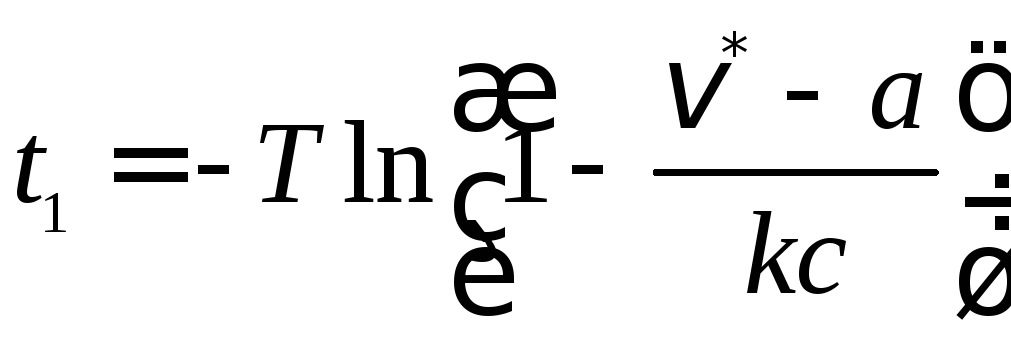 .
.
По первой формуле (2.33) определяем
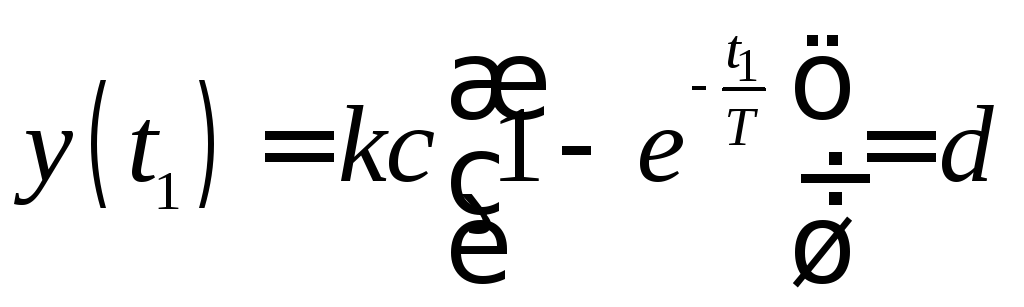 .
.
Конечное значение
процесса
![]() принимаем за начальное для второй
формулы (2.33), тогда получим
принимаем за начальное для второй
формулы (2.33), тогда получим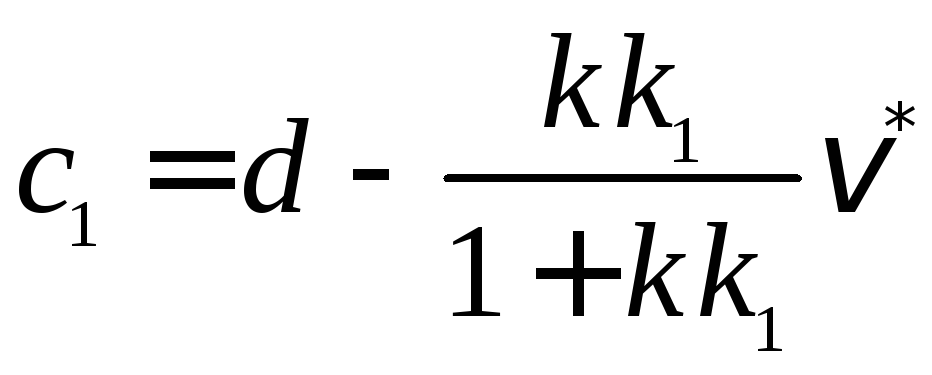 и
и
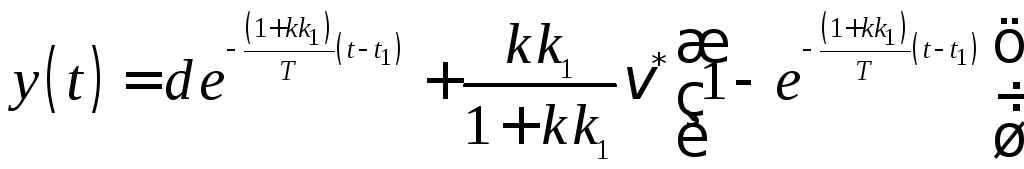 . (2.34)
. (2.34)
Итак, закон изменения
координаты
![]() при
при![]() и
и![]()
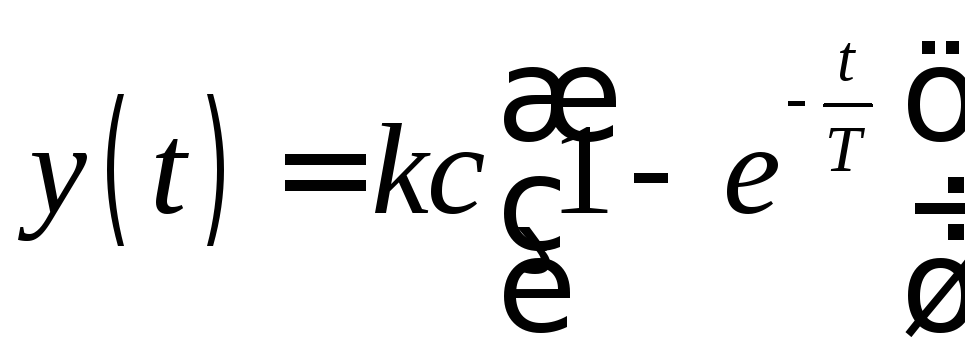 ,
,![]() . (2.35)
. (2.35)
Если же
![]() ,
то при
,
то при![]() выход будет изменяться по закону (2.35),
а далее при
выход будет изменяться по закону (2.35),
а далее при![]() закон изменения будет (2.34).
закон изменения будет (2.34).
При
![]() в первом случае на выходе имеем
установившееся значение
в первом случае на выходе имеем
установившееся значение![]() ,
а во втором
,
а во втором .
.
