2.8. Коррекция нелинейных систем

При синтезе нелинейных систем кроме классической задачи коррекции САУ по точности, устойчивости, качеству решаются специфические задачи: подавление автоколебаний или организация колебаний с определенными значениями амплитуды и частоты. При этом применяются цепи обратной связи, вибрационное сглаживание, другие методы.

2.8.1. Коррекция нелинейной системы с помощью обратной связи

Рассмотрим метод подавления автоколебаний, основанный на введении обратной связи, охватывающей нелинейный элемент и часть линейной системы (рис. 2.22). Предполагается, что НЭ относится к статическому типу.

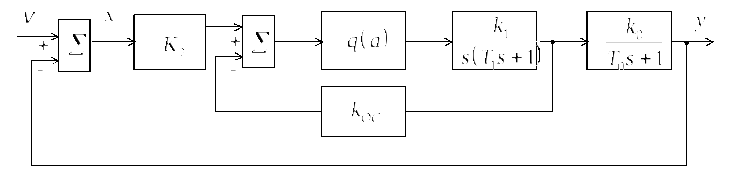
Рис. 2.22

Запишем характеристическое уравнение гармонически линеаризованной замкнутой системы:

, (2.75)

где – гармонически линеаризованный коэффициент усиления нелинейного элемента.

В соответствии с критерием устойчивости Гурвица система третьего порядка будет находиться на границе устойчивости при условии:

. (2.76)

По данному выражению можно построить границу устойчивости системы в области интересующих параметров, задаваясь максимальным значением характеристики нелинейного элемента. Например, для идеального двухпозиционного реле , и тогда максимальное значение, соответствующее границе устойчивости НСАУ, войдет в соотношения:

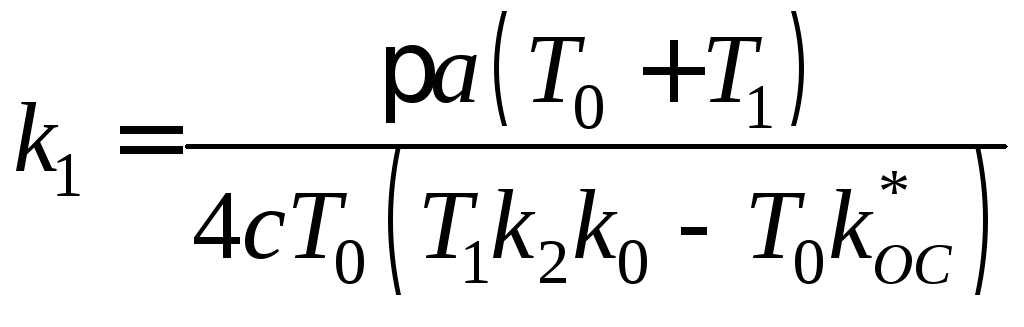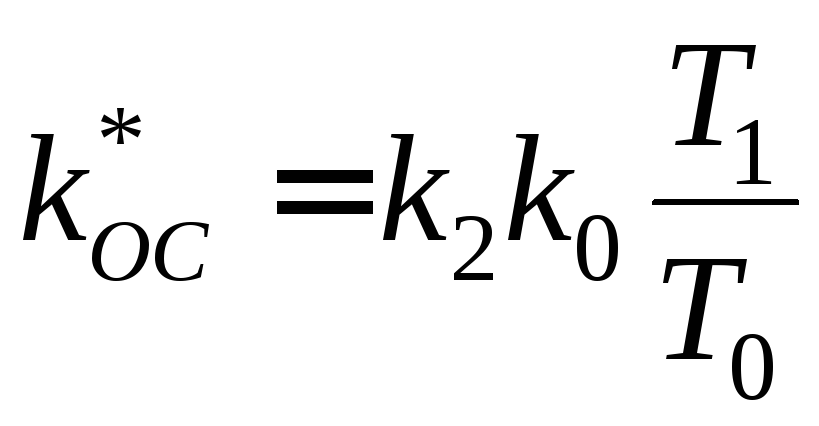,. (2.77)

Из (2.77) при известных значениях, например, находятся предельные значенияи. Для обеспечения устойчивости НСАУ значенияидолжны быть выбраны так, чтобы они попали в область, соответствующую отсутствию автоколебаний.

2.8.2. Коррекция нелинейной системы с помощью вибрационного сглаживания

Вибрационное сглаживание (вибрационная линеаризация) применяется для подавления автоколебаний и устранения влияния нелинейностей типа люфт, зона насыщения, реле и др.

Пусть на вход НЭ (рис. 2.23) подан дополнительный сигнал , причем медленно меняющаяся составляющаяудовлетворяет условию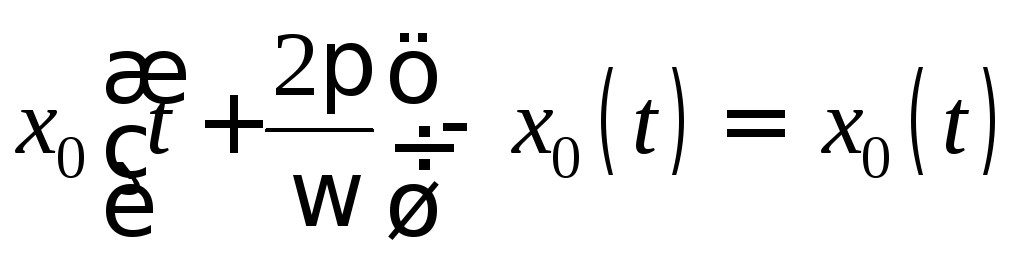, а частотанаходится за полосой пропускания линейного звена.

Рис. 2.23

Сигнал на выходе НЭ содержит две составляющих

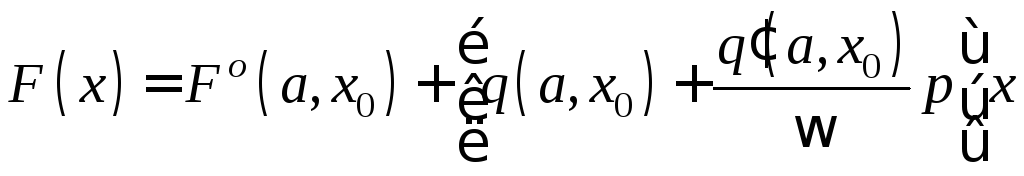, (2.78)

где постоянная составляющая (функция смещения), например, для идеального двухпозиционного реле

. (2.79)

Зависимость (2.79) имеет вид, приведенный на рис. 2.24. При малых значениях – это линейная зависимость, где.

Для указанного НЭ

.

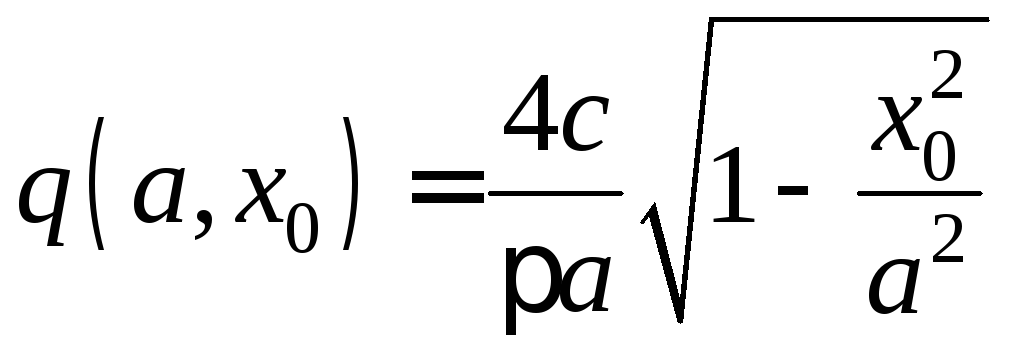
Рис. 2.24

Однако в силу принятых допущений не пропускает гармонику, т.е. колебания локализируются во внутреннем контуре. Так осуществляется вибрационное сглаживание.

При этом частота дополнительного сигнала, как отмечалось ранее, , где– полоса пропускания линейного звена, а амплитудадолжна выбираться из условия. Дополнительный сигнал вводят, применяя специальный генератор синусоидальных колебаний, либо организуя собственные колебания путем введения местной гибкой отрицательной обратной связи.

В зависимости от структуры системы и типа нелинейных элементов применяются и другие способы построения регуляторов.

3. Случайные процессы в системах автоматического управления

3.1. Случайные процессы и их характеристики

Прежде чем дать определение случайного процесса напомним основные понятия из теории случайных величин. Как известно, случайной величиной называется величина, которая в результате опыта может принять то или иное значение, заранее неизвестное. Различают дискретные и непрерывные случайные величины. Основной характеристикой случайной величины является закон распределения, который может быть задан в виде графика или в аналитической форме. При интегральном законе распределения функция распределения , где– вероятность того, что текущее значение случайной величиныменьше некоторого значения. При дифференциальном законе распределения используют плотность вероятности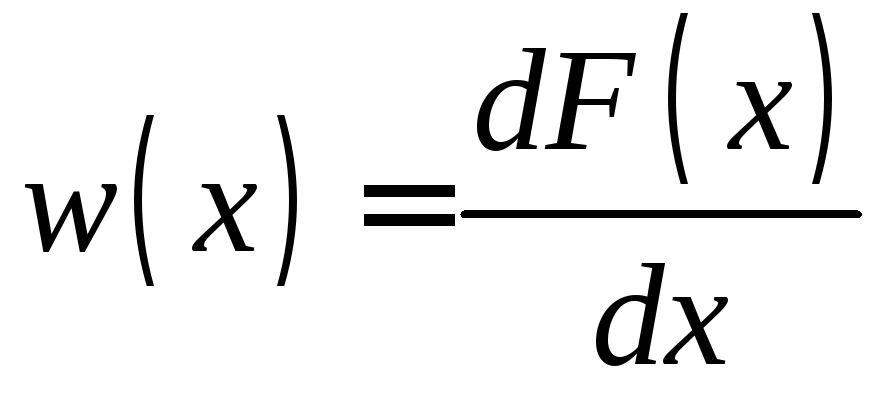. Численными характеристиками случайных величин являются так называемые моменты, из которых наиболее употребительны момент первого порядка – среднее значение (математическое ожидание) случайной величины и центральный момент второго порядка – дисперсия. В случае, если имеется несколько случайных величин (система случайных величин), вводится понятие корреляционного момента.

Обобщением понятия случайной величины является понятие случайной функции, т.е. функции, которая в результате опыта может принять тот или иной вид, неизвестный заранее. Если аргументом функции является время t, то её называют случайным или стохастическим процессом.

Конкретный вид случайного процесса, полученный в результате опыта, называется реализацией случайного процесса и является обычной неслучайной (детерминированной) функцией. С другой стороны в фиксированный момент времени имеем так называемое сечение случайного процесса в виде случайной величины.

Для описания случайных процессов обобщаются естественным образом понятия теории случайных величин. Для некоторого фиксированного момента времени, случайный процесс превращается в случайную величину , для которой можно ввести функцию , называемую одномерным законом распределения случайного процесса . Одномерный закон распределения не является исчерпывающей характеристикой случайного процесса. Он, например, не характеризует корреляцию (связь) между отдельными сечениями случайного процесса. Если взять два разных момента времении, можно ввести двумерный закон распределенияи т.д. В пределах нашего дальнейшего рассмотрения будем ограничиваться в основном одномерным и двумерным законами.

Рассмотрим простейшие характеристики случайного процесса, аналогичные числовым характеристикам случайной величины. Математическое ожидание или среднее по множеству

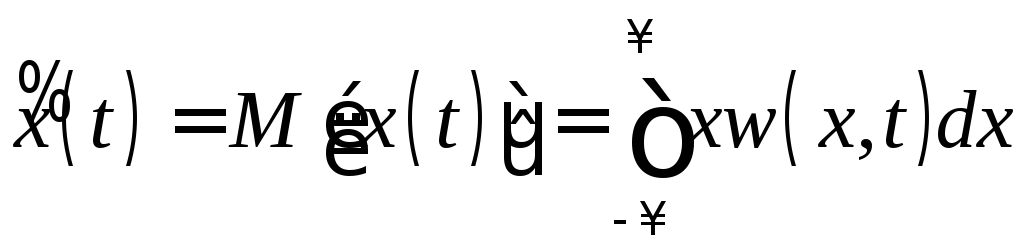(3.1)

и дисперсию

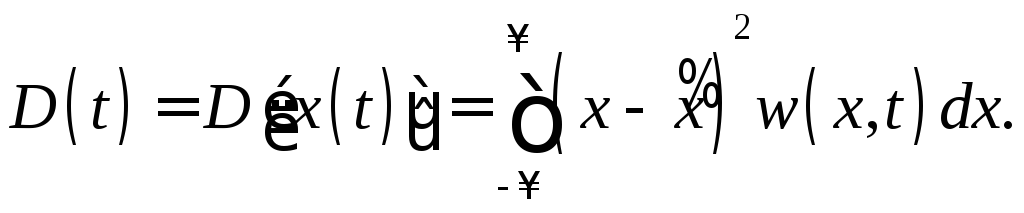(3.2)

Математическое ожидание – это некоторая средняя кривая, вокруг которой группируются отдельные реализации случайного процесса, а дисперсияхарактеризует в каждый момент времени разброс возможных реализаций. Иногда, используется среднеквадратичное отклонение .

Для характеристики внутренней структуры случайного процесса вводится понятие корреляционной (автокорреляционной) функции

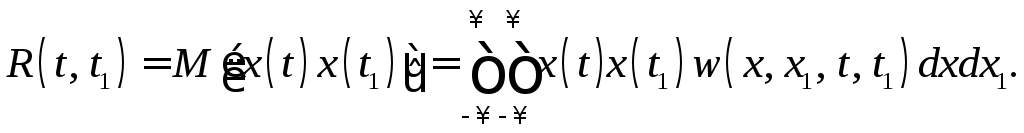(3.3)

Наряду с математическим ожиданием (среднее по множеству) (3.1) вводится ещё одна характеристика случайного процесса – среднее значение случайного процесса для отдельной реализации (среднее по времени)

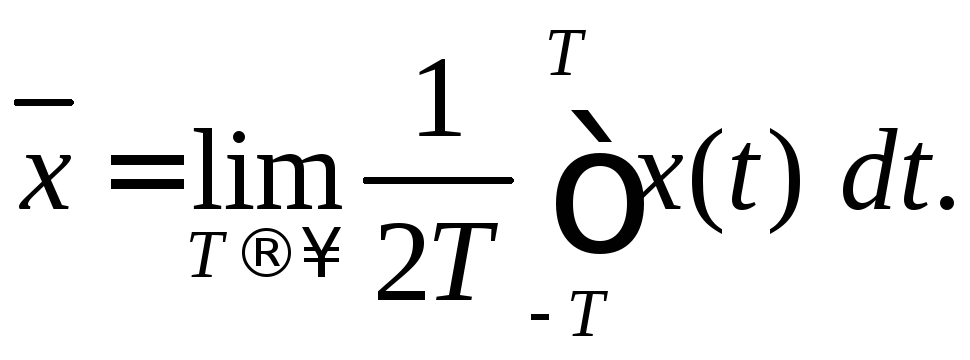(3.4)

Для двух случайных процессов можно также ввести понятие взаимной корреляционной функции по аналогии с (3.3).

Одним из частных случаев случайного процесса, находящих широкое применение на практике, является стационарный случайный процесс – это случайный процесс, вероятностные характеристики, которого не зависят от времени. Итак, для стационарного случайного процесса ,, а корреляционная функциязависит от разности, т.е. является функцией одного аргумента.

Стационарный случайный процесс в какой-то мере аналогичен обычным или установившимся процессам в системах управления.

Стационарные случайные процессы обладают интересным свойством, которое называется эргодической гипотезой. Для стационарного случайного процесса всякое среднее по множеству равно среднему по времени. В частности, например, Это свойство позволяет часто упростить физическое и математическое моделирование систем при случайных воздействиях.

Как известно, при анализе детерминированных сигналов широкое применение находят их спектральные характеристики на базе ряда или интеграла Фурье. Аналогичное понятие можно ввести и для случайных стационарных процессов. Отличие будет заключаться в том, что для случайного процесса амплитуды гармонических составляющих будут случайными, а спектр статического случайного процесса будет описывать распределение дисперсий по различным частотам.

Спектральная плотность стационарного случайного процесса связана с его корреляционной функциейпреобразованиями Фурье:

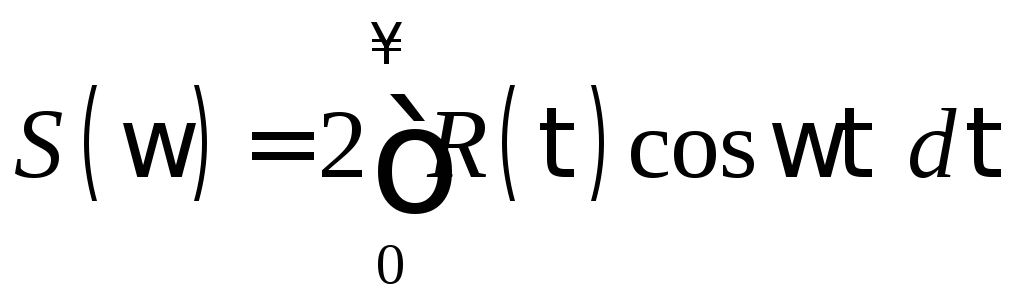, (3.5)

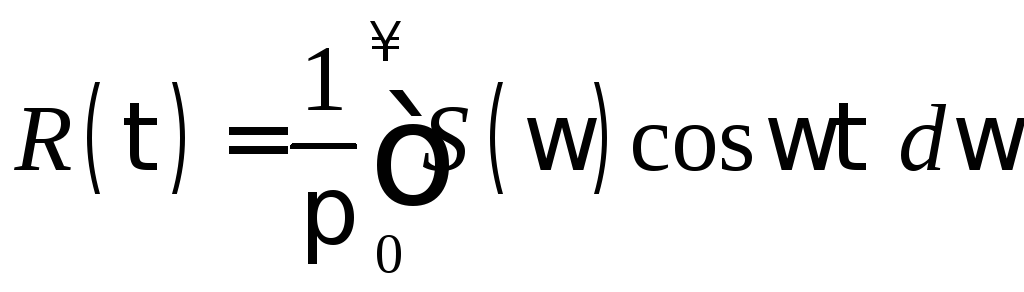, (3.6)

где корреляционную функцию будем трактовать как оригинал, а   как изображение.

Существуют таблицы, связывающие оригиналы и изображения . Например, если, то.

Отметим связь спектральной плотности и корреляционной функции с дисперсией D

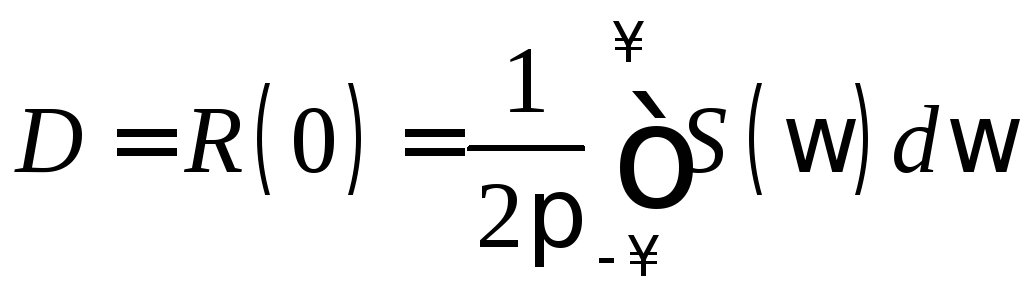. (3.7)

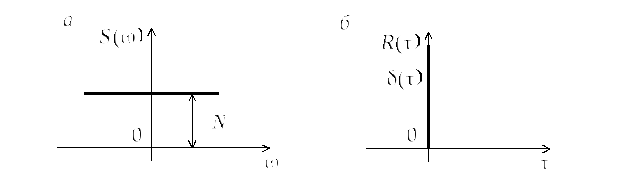
В заключение рассмотрим свойства “белого шума”. Под белым шумом понимают случайный процесс, спектральная плотность которого постоянна при всех частотах от до, т.е.(рис.3.1,а).

Рис. 3.1

Корреляционная функция в соответствии с (3.6)

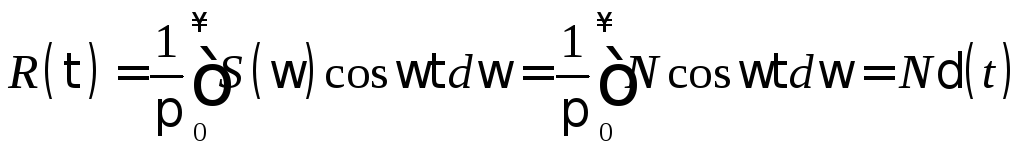. (3.8)

График приведен на рис. 3.1, б.

Пример 3.1. Для стационарного случайного процесса со свойствами белого шума в ограниченной полосе частот от до(рис. 3.2, а) определить дисперсию и корреляционную функцию.

На основании (3.7) .

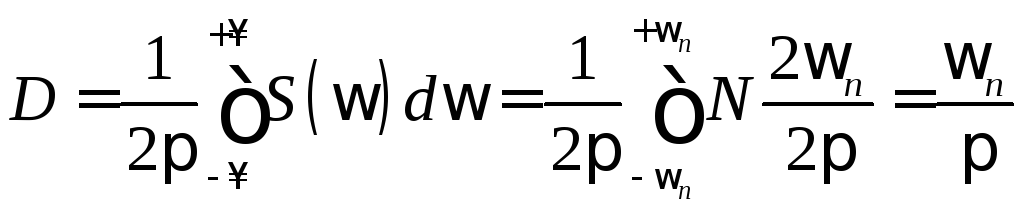Корреляционная функция в силу (3.6) 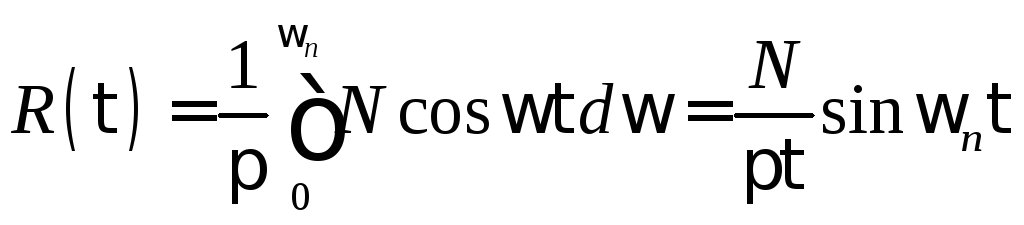. Её график изображён на рис. 3.2, б.

Рис. 3.2

В приводятся графики зависимостейидля различных реализаций случайных процессов.