
- •1.Введение
- •2.Траектория и путь м.Т. Ск-ть м.Т.
- •3.Ускорение м.Т.
- •4.Поступат. И вращат. Движ. Тв. Тела.
- •6. Масса и Импульс тела
- •7.Центр масс
- •8.Закон сохранения импульса
- •9.Движение тела перем. Массы
- •10.Момент силы
- •11.Момент импульса
- •11.Закон сохранения момента импульса
- •13.Момент инерции
- •14.Энергия
- •15.Кинетическая энергия. Работа
- •16.Потенциальные (консервативные) силы. Потенциальная энергия
- •17.Закон сохр. Полной мех. Энергии
- •18.Кинетическая энергия вращательного движения
- •19.Плоское движение. Кинетическая энергия плоского движения
- •20.Неинерциальные системы отсчета
- •21.Колебание. Типы колебаний
- •22.Гармонические колебания
- •23.Метод вект. Диаграмм
- •24.Сложение двух гармонических колебаний
- •25.Упругая сила. Энергия гармонических колебаний
- •26.Потенциальная энергия. Полная энергия гармонич. Колебаний.
- •27.Пружинный маятник. Физический маятник
- •28.Математический маятник. Приведённая длина физического маятника
- •29.Затухающие механические колебания
- •30.Вынужденные механические колебания.
- •31.Упругие волны.Продольные и поперечные волны в упругой среде
- •32.Типы волн и их характеристики. Плоская синусоидальная волна
- •33.Сферическая и стоячие волны
- •34.Фазовая скорость упругих волн в твердой среде
- •35.Энергия упругой волны
- •36.Принцин относительности Галилея или преобразования Галилея
- •37.Специальная теория относительности. Преобразования Лоренца
- •38.Изменение длины тела
- •39.Промежуток времени между событиями
- •40.Основной закон релятивистской динамики
- •41.Релятивистский закон взаимодействия массы и энергии
- •42.Ур-ние Бернулли
- •43.Формула Торричелли. Ламинарный и турбулентный режимы движения вязкой среды
- •44.Статистический, динамический и термодинамический методы исследования.
- •45.Ф-я распределения вероятности
- •46.Распределение Максвелла.Средняя, среднеквадратичная и наивероятная скорости молекул.
- •47.Распределения Больцмана. Барометрическая формула
- •48.Ур-ние состояния идеальных газов
- •49.Число степеней свободы.Внутренняя энергия газа
- •50.Теплоемкость газов
27.Пружинный маятник. Физический маятник
Примером
линейного гармонического осциллятора
м.т., совершающей прямолинейные гармонич.
колеб. под действием упругой силы
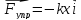 может служить пружинный маятник.
Пружинный маятник – это груз массойm
подвешенный на абс. упругой пружине с
коэф. упругости k,
характеризующим упругие св-ва пружины,
ДУ движения такой системы запишется в
виде
может служить пружинный маятник.
Пружинный маятник – это груз массойm
подвешенный на абс. упругой пружине с
коэф. упругости k,
характеризующим упругие св-ва пружины,
ДУ движения такой системы запишется в
виде
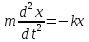 или
или
Решение
этого ДУ явл. ф-я
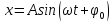 с
циклич. частотой, равной
с
циклич. частотой, равной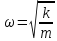 и периодом
и периодом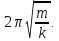
Физич.
маятник – тв. тело, имеющее возможность
качаться под действием силы тяжести
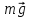 вокруг неподвижно горизонтальной оси
О, не проходящей через центр тяжести
тела, и называемой осью подвеса.
вокруг неподвижно горизонтальной оси
О, не проходящей через центр тяжести
тела, и называемой осью подвеса.
Центр тяжести физ. маятника совпадает с его центром инерции.

В
отсутствие сил трения в оси подвеса ДУ
движения маятника имеет вид
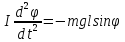 ,
где
,
где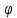 - угол поворота маятника вокруг оси
подвеса из положения равновесия;
- угол поворота маятника вокруг оси
подвеса из положения равновесия;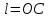 – расст. от центра инерции(масс) маятника
до точки подвеса О.
– расст. от центра инерции(масс) маятника
до точки подвеса О.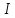 - мом. инерции маятника относит. оси
подвеса;m
– масса маятника.
- мом. инерции маятника относит. оси
подвеса;m
– масса маятника.
При
малых колебаниях физ. маятника
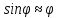 и ур-ние движения физ. маятника принимает
вид
и ур-ние движения физ. маятника принимает
вид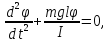 где
где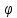 удовлетворяет ДУ гармонич. колебаний.
Таким образом, в отсутствие сил трения
в оси подвеса малые колебания физ.
маятника явл. гармоническими, т.е.
удовлетворяет ДУ гармонич. колебаний.
Таким образом, в отсутствие сил трения
в оси подвеса малые колебания физ.
маятника явл. гармоническими, т.е.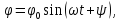 где
где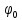 – амплитуда колебаний угла
– амплитуда колебаний угла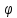 ,
а
,
а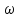 - циклич. частота, равная
- циклич. частота, равная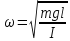 с периодом
с периодом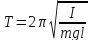 .
.
28.Математический маятник. Приведённая длина физического маятника
Матем. маятник – м.т., подвешенная на невесомой нерастяжимой нити и совершающая колеб. в вертикальной плоскости под действием силы тяжести.
Матем.
маятник представляет собой предельный
случай физ. маятника, вся масса кот.
сосредоточена в его центре инерции так,
что
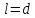 ,
где
,
где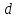 - длина нити матем. маятника.
- длина нити матем. маятника.
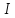 такого
маятника как м.т. относительно оси
подвеса =
такого
маятника как м.т. относительно оси
подвеса =
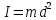 ,
тогда циклич. частота
,
тогда циклич. частота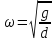 ,
а период малых колеб.
,
а период малых колеб.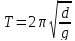 .
.
Для
матем. и физ. маятников для периодов мы
имеем формулу
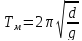
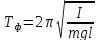
Если
подобрать параметры этих маятников
таким образом, чтобы их периоды совпадали,
тогда будем иметь равенство
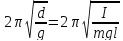 или
или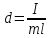
Т.е.
для того, чтобы периоды физ. и матем.
маятников совпадали, необходимо,чтобы
их длины удовлетворяли условию
 ,
где
,
где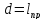 - наз. приведенной длиной физ. маятника.
Точка на прямой, соединяющая точку
подвеса и центром масс и лежащая на
расстоянии приведенной длины от оси
подвеса, наз. центром качания физ.
маятника.
- наз. приведенной длиной физ. маятника.
Точка на прямой, соединяющая точку
подвеса и центром масс и лежащая на
расстоянии приведенной длины от оси
подвеса, наз. центром качания физ.
маятника.
По
теореме Штейнера для момента инерции
физ. маятника мы имеем формулу
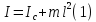 ,
где
,
где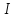 – момент инерции физ. маятника относительно
оси подвеса;
– момент инерции физ. маятника относительно
оси подвеса;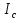 - момент инерции его относительно оси,
проходящей через центр масс, или центр
инерции и || оси инерции относительно
оси подвеса.
- момент инерции его относительно оси,
проходящей через центр масс, или центр
инерции и || оси инерции относительно
оси подвеса.
Разделив
левую и правую часть ур-ния (1) на
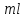 , получим:
, получим: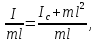 но
но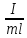 есть
есть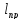 , тогда
, тогда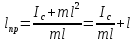 ,
т.е. приведенная длина физ. маятника
всегда больше
,
т.е. приведенная длина физ. маятника
всегда больше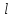 ,
а точка подвеса и центр качанияO’
лежат по разные стороны от центра масс.
Эти точки (подвеса и качания) обладают
тем св-вом, что период колебаний физ.
маятника не изменяется, если поменять
их местами.
,
а точка подвеса и центр качанияO’
лежат по разные стороны от центра масс.
Эти точки (подвеса и качания) обладают
тем св-вом, что период колебаний физ.
маятника не изменяется, если поменять
их местами.
29.Затухающие механические колебания
Затуханием колебаний наз. постепенное ослабление колебаний с теч. времени, обусловленное потерей энергии колеб. сист.
Затухание свободных мех. колеб. вызывается главным образом трением и возбуждением в окружающей среде упругих волн. Закон затухания зависит от св-ств колебательной системы. Системы наз линейной, если параметры, характеризующие существенные в рассматриваемом процессе физ. св-ва системы не изменяются в ходе процесса, напр. пружинный маятник не изменяется в ходе процесса (пруж. маятник, движущийся в вязкой среде, представляет собой лин. сист., если сопротивление среды и упругость пружины не зависят от смещения и скорости маятника).
Наиболее
часто встречающейся силой, приводящей
к затуханию колебания, явл. сила трения
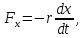 где
где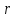 – коэф. трения. Знак “-” потому, что
сила трения и ск-ть направлены в
противоположные стороны.
– коэф. трения. Знак “-” потому, что
сила трения и ск-ть направлены в
противоположные стороны.
Динамическое
ур-ние 2-го закона Ньютона при наличии
силы трения запис. в виде:
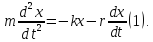
Если
ввести коэф. затухания
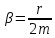 и записать
и записать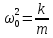 ,
где
,
где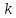 – коэф. упругости пружины,
– коэф. упругости пружины,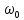 - циклич. частота свободных незатухающих
колебаний той же системы, т.е. в отсутствие
потерь энергии, то ур-ние (1) запишется
в виде:
- циклич. частота свободных незатухающих
колебаний той же системы, т.е. в отсутствие
потерь энергии, то ур-ние (1) запишется
в виде:
Решением
такого ур-ния явл. ф-я
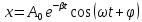 ,
где
,
где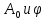 – постоянные, зависящие от нач. условие;
– постоянные, зависящие от нач. условие;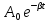 - амплитуда затухающих колеб.
- амплитуда затухающих колеб.
Циклич.
частота затухающих колеб. =
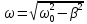 ,
где
,
где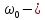 циклич.
частота свободных колебаний;
циклич.
частота свободных колебаний;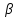 – коэф. затухания.
– коэф. затухания.
Тогда
период затух. колеб.
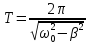 .
.
Рассм.
некоторые физ. величины, кот. хар-ют
затух. колеб. Отношение значений амплитуды
отличающихся друг от друга на период T
и равная
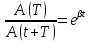 (1) наз.декрементом затухания, а его (2)
(1) наз.декрементом затухания, а его (2)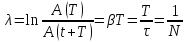 наз. логарифмическим декрементом
затухания, где
наз. логарифмическим декрементом
затухания, где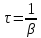 – промежуток времени, в теч. кот. амплитуда
затух. колебаний уменьшается в
– промежуток времени, в теч. кот. амплитуда
затух. колебаний уменьшается в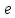 раз
и величина
раз
и величина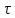 наз. временем релаксации,N-
число колебаний, в теч. которого амплитуда
уменьшается в
наз. временем релаксации,N-
число колебаний, в теч. которого амплитуда
уменьшается в
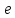 раз.
раз.
Связь
между циклич. частотой
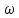 затух. колебаний системы и логарифмическим
декрементом затухания след.:
затух. колебаний системы и логарифмическим
декрементом затухания след.:
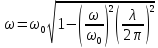
Добротностью
колеб. сист. наз. безразмерная величина
Q,
равная произведению
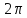 на
отношение энергииE(t)
колебательной системы в произвольный
момент времени t
к убыли этой энергии за промежуток
времени от t
до t+T
, т.е. за один условный период затухающих
колебаний
на
отношение энергииE(t)
колебательной системы в произвольный
момент времени t
к убыли этой энергии за промежуток
времени от t
до t+T
, т.е. за один условный период затухающих
колебаний
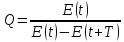
Т.к.
энергия пропорциональна квадрату
амплитуды A(t),
то
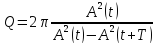
Поскольку
для затухающих колеб.
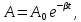 то добротность равна
то добротность равна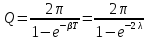
При
малых значениях логарифмического
декремента затухания
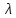 колебания почти не затухающиеT=T0
и значения для Q
принимает вид
колебания почти не затухающиеT=T0
и значения для Q
принимает вид
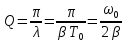 , где
, где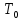 и
и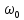 - период и циклич. частота свободных
колебаний.
- период и циклич. частота свободных
колебаний.
