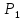- •4. Полярная система координат на плоскости.
- •5. Прямоугольные декартовые координаты пространств.
- •9. Угол между двумя прямыми. Расстояние от точки до прямой.
- •10. Линии второго порядка. Окружность.
- •11.Линии второго порядка.Эллипс
- •12. Линии второго порядка.Гипербола.
- •13 Линии второго порядка. Парабола
- •14 .Основные понятия и определения. Теория матрицы
- •15. Линейные действия над матрицами
- •16.Произведение матриц
- •17.Транспонировние матрицы
- •18. Определители 2-ого и 3-ого порядков.
- •19. Обратная матрица
- •20. Ранг матрицы
- •21. Система линейных уравнений. Основные понятия
- •22.Решение систем линейных уравнений с помощью определителя(теорема Крамера)
- •23. Исследование систем линейных уравнений (теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)
- •24.Матричный метод решения систем линейных уравнений
- •25)Метод Гаусса решения систем линейных уравнений.
- •29.Умножение вектора на число. Свойства линейных операций над векторами.
- •31. Составляющие вектора: на плоскости, по прямой и плоскости, по трем прямым
- •Вопрос32. Разложение вектора по базису
- •Вопрос33.Прямоугольные декартовы координаты в пространстве
- •34. Длина вектора. Линейные операции над векторами в прямоугольных координатах: сумма, разность, умножение на число. Признак коллинеарности двух векторов в прямоугольных координатах.
- •35. Скалярное произведение векторов
- •37.Смешанное произведение 3 векторов.
- •38. Линейная зависимость векторов
- •39.Уравнение поверхности и линии
- •Уравнение плоскости, проходящей через три точки
- •41. Прямая в пространстве (направляющий вектор, каноническое уравнение) .Параметрическое уравнение прямой. Уравнение прямой, проходящей через две данные точки
- •44. Понятие сложной функции. Четные и нечетные функции, переодические функции.Основные элементарные функции.
- •45. Функция натурального аргументы и ее предел.
- •47. Предел функции в точке и на бескон. Определение
- •49. Основныесв-ва пределов функций.
- •50.Замечательные пределы
- •51. Непрерывные ф-ции.Точки разрыва ,их классификация.
12. Линии второго порядка.Гипербола.
Гиперболой назовём геометрическое место точек плоскости, для каждой из которых модуль разности расстояний от двух данных точек этой же плоскости, называемых фокусами ,является постоянной величиной(равной 2a).
Если
оси координат расположены по отношению
к гиперболе так , что фокусы гиперболы
находятся на оси абсцисс на равных
расстояниях от начала координат в точках
F1(-c,0)
и F2(c,0),
то ур-ние гиперболы имеет канонический
вид:
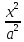 ˗
˗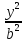 =1
гдеc=
=1
гдеc=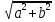 .
.
При этом ОА = а есть действительная полуось ,а ОВ = b есть мнимая полуось гиперболы. Начало координат О ˗ центр гиперболы. Точки А(а,0) и С (-а,0) ,пересечения гиперболы с осью Ох назовём вершинами гиперболы.
Эксцентриситетом
гиперболы назовём отношение фокусного
расстояния 2с к длине действительной
оси 2а,то есть :
 =
= .
.
В виду того, что с > а ,эксцентриситет гиперболы ɛ >1.
Асимптотами
гиперболы назовём прямые :y=
 x
и y=
˗
x
и y=
˗
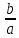 x.
x.
Расстояние некоторой точки М гиперболы до её фокусов F1 и F2 назовём фокальными радиусами-векторами точки М и обозначим соответственно r1 и r2. Точки ,для которых r1 –r2=2a, принадлежат правой ветви гиперболы ,а точки ,для которых r2-r1=2a, принадлежат левой ветви гиперболы.
Фокальные радиусы-векторы точки правой ветви гиперболы вычисляются по формулам : r1 = ɛx +a; r2 = ɛx ˗a; фокальные радиус-векторы точки левой ветви гиперболы вычисляются по формулам : r1 = ˗ɛx ˗a; r2 = ˗ɛx + a.
В частном случае, когда а =b,гиперболу назовём равносторонней, а её каноническое уравнение будет иметь вид :x2 ˗ y2 = a2.
Уравнение
гиперболы в полярных координатах: ƿ =
 , где фокальный параметр p =
, где фокальный параметр p =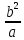 , оно определяет одну ветвь гиперболы.
, оно определяет одну ветвь гиперболы.
Директрисы
– прямые, перпендикулярные к действительной
оси и расположены на расстоянии d
=
 от её центра. Уравнениями директрис
гиперболы являются :x
= ˗
от её центра. Уравнениями директрис
гиперболы являются :x
= ˗
 ,x
=
,x
=
 :
:
Гиперболы
: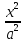 -
- = 1 и
= 1 и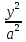 -
-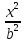 =1 назовём сопряжёнными. У сопряжённых
гипербол общие асимптоты .Действительная
ось одной из них совпадает с мнимой осью
другой, и наоборот.
=1 назовём сопряжёнными. У сопряжённых
гипербол общие асимптоты .Действительная
ось одной из них совпадает с мнимой осью
другой, и наоборот.
Геометрическое место точек, определяемое уравнением второй степени :
xy
= a
(a
≠ 0) ,является равносторонней гиперболой.
Это уравнение обычно записывают в виде
:y
=
 .
.
её
асимптотами являются координаты оси
0х и 0у. Если а >0, то ветви гиперболы
расположенные в первом и третьем
квадрантах , а если а <0, то ветви
гиперболы расположены во втором и
четвёртом квадрантах.
13 Линии второго порядка. Парабола
Парабола – геометрическое место точки плоскости, равноудаленное от данной точки(фокуса) и данной прямой(директрисы), лежащих в той же плоскости.
Каноническое уравнение параболы симметрично относительно оси ОХ и проходит через начало координат(рис 1) имеет вид
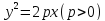
Уравнение
ее директрисы
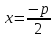 ,
а фокус расположен в т.F(
,
а фокус расположен в т.F(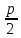 ;0)
на расстоянии
;0)
на расстоянии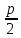 от вершины параболы О(0;0). Ось ОХ назовем
осью параболы, число р – фокальным
параметром параболы. Эксцентриситет
параболы равен 1.
от вершины параболы О(0;0). Ось ОХ назовем
осью параболы, число р – фокальным
параметром параболы. Эксцентриситет
параболы равен 1.
Расстояние т.М параболы до фокуса F назовем фокальным радус-вектором т.М обозначим r
Фокальный радиус-вектор т.М(х; у)равен


14 .Основные понятия и определения. Теория матрицы
Матрицы – прямоугольный массив чисел, записанный в виде строк и столбцов. Строки и столбцы называются ее рядами.
Матричной
записью пользуются во всех областях
знаний. Например, если надо нормы расходов
и видов ресурсов на изготовление единицы
каждого из 3-ех видов продукции
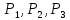 ,
то это удобно написать в виде таблицы
,
то это удобно написать в виде таблицы
|
Ресурсы |
Вид продукции | ||
|
|
|
| |
|
Сырье |
1,4 |
2,4 |
0,8 |
|
Электроэнергия |
1,0 |
0,6 |
1,6 |
|
Оборудование |
2,0 |
1,0 |
3,0 |
|
Труд |
1,7 |
2,3 |
1,5 |

В
случае необходимо приведенное в таблице
число записывать в более компактной
форме, в которой содержится значение
каждого показателя, определяющего его
местоположение. Так число 1,6 означает
затраты электроэнергии на изготовление
единицы продукции вида
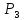 .
Записанный таким образом массив чисел
называетсяматрицы,
а числа в массиве – элементы
матрицы.
.
Записанный таким образом массив чисел
называетсяматрицы,
а числа в массиве – элементы
матрицы.
Матрицы обозначают прописными буквами латинского алфавита: А, В, С … , а их элементы строчными: а, b, с … . Для обозначения каждого из элементов матрицы используют 2-ые индексы: 1-ый означает номер строки, 2-ой – номер столбца.
Так
 означает элемент стоящий вi-той
строке j-том
столбце.
означает элемент стоящий вi-той
строке j-том
столбце.
В общем случае матрицы, состоящие из m строк и n столбцов, записывают в виде
А= (1)
(1)
Иногда
используют сокращенные записи
 ;
(
;
( )
)
Иногда (m*n)читается как «m на n», означает размерность матрицы. В примере приведенном выше размерность матрицы равна 4*3
Если число строк матрицы равна число столбцов матрицы, т.е. m=n,то матрица называется квадратного порядка n, т.е
А= (2)
(2)
Говорят,
что элемент в строке
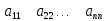 квадратной матрицы (2) образуют ееглавную
диагональ,
а элементы
квадратной матрицы (2) образуют ееглавную
диагональ,
а элементы
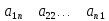 -вторую
(побочную) диагональ.
-вторую
(побочную) диагональ.
Квадратная матрица называется симметричной, если равны ее элементы симметричны относительно главной диагонали. Например:

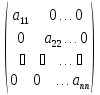
Диагональной матрицей называется квадратная матрица, у которой все элементы, которые не принадлежат главной диагонали, равны 0. Например:

Обозначим
diag( )=
)= (3)
(3)
Если все элементы главной диагонали матрицы (3) равны 1, то матрицу называют единичной(Е).
Е=
Если в квадратной матрице все элементы, лежащие выше или ниже главной диагонали равны 0, то ее называют треугольной. Например:
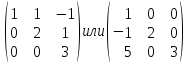
Матрицу называют нулевой, если все ее элементы равны 0
0=
2 матрицы одинаковой размерности называют равными, если равны их элементы, состоящие на соответствующих местах.
Матрицы, состоящие из 1-ой строки – матрицой-строкой, а из 1-ого столбца – матрицой-столбцом.