The Physics of Coronory Blood Flow - M. Zamir

88 3 Basic Lumped Elements

take place more forcefully so that the spring will overshoot its equilibrium length and bounce back.

Which of the two scenarios occurs depends on the rate at which the flow rate diminishes, which in turn depends on the relative values of the inertial and capacitance e ects. Recalling that tL = L/R, tC = RC, if the value of the ratio 4tL/tC is below 1.0, the balloon does not recoil, as seen in the top curve in Fig. 3.3.1. If the value of the ratio is higher than 1.0, the balloon recoils, leading to the oscillations seen in the bottom curve. One particular value of that ratio, namely that corresponding to 4tL/tC = 1.0, is referred to as “critically damped” in the sense that it acts as a separating line between the two types of behaviour, as shown by the middle curve in Fig. 3.4.1.

The free dynamics of a dynamical system do not represent its dynamics under the action of external forces, which is referred to as “forced dynamics”, but they do represent the intrinsic characteristics of the system. An understanding of these characteristics is important because they ultimately determine how the system responds to external forces.

In the dynamics of the coronary circulation, the above scenarios are relevant to the extent that the elements of inductance, resistance, and capacitance, are known to exist in that system. While it is generally believed that these elements are arranged in parallel rather than in series as they are here, and while the dynamics of the coronary circulation is generally forced rather than free, some of the overall conclusions reached here are relevant nevertheless. More specifically, a change in the relative values of R, L, C, that may occur as a result of disease or surgery, may change the intrinsic characteristics of the system and hence its dynamic behaviour. Thus, a narrowing or sti ening of some coronary arteries may change not only the values of R and C and the corresponding resistance and capacitance e ects, but it may cause the system to cross over from one type of dynamic behaviour to another. Similarly, a change in the consistency of blood resulting from the administration of certain drugs which may change the density and viscosity of blood, may not only change the values of L and R but may lead to a change in the dynamic behaviour of the system.

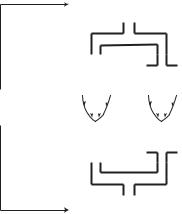
3.4 R1,R2 in Parallel

When elements of the lumped model are in series, as we have seen in this chapter so far, the flow rate through all elements at any moment in time must be the same because of the law of conservation of mass. When the elements are in parallel, however, this is no longer the case, as we saw in Section 2.6 where capacitance and resistance were in parallel. This is because when two elements opposing the flow are in parallel, flow rate through the system is divided in a manner commensurate with the relative opposition presented by each element.

3.4 R1,R2 in Parallel

89

This division of flow is an important property of parallel systems, which is particularly significant in coronary blood flow and in blood flow in general. It allows di erent flow rates to prevail simultaneously within the system, which is not possible when the elements are in series. We shall see in the next chapter that this di erence between series and parallel flow systems provides an important tool in the construction of a lumped model of the coronary circulation. In the remainder of this chapter we explore some basic parallel arrangements to highlight their properties, starting with two di erent resistances in parallel as shown in Fig. 3.4.1. Only elementary properties pertaining particularly to the parallel arrangement are discussed. In each case, the full dynamics of these systems are deferred to subsequent chapters.

p2

p = p2 - p1

R1

R2

p1

Fig. 3.4.1. Two resistances in parallel, represented schematically by fully developed Poiseuille flow in two tubes in parallel under a driving pressure drop Δp. A parallel system allows di erent flow rates to prevail simultaneously within the system, which is not possible when the elements are in series.

The scenario usually considered in this case is one in which the pressure drop Δp is constant, so any change in one or both resistances will a ect only the flow rates. The pressure drops across the two elements will not change because they are both the same under the parallel arrangement and are both equal to the constant value of Δp under this scenario. However, another important scenario to consider is that in which the total flow rate through the system is constant. This condition is likely to arise in the physiological system because of regulatory mechanisms that respond to local oxygen consumption by cardiac tissue, which is related to flow rate rather than to pressure. A change in one or both resistances in this case will a ect not only the individual flow rates through the two elements but also the pressure drop across the system, because the pressure drop must change in order to maintain the

90 3 Basic Lumped Elements

prescribed constant flow rate through the system. Let us consider these two scenarios in more detail.

Under the scenario of constant pressure drop Δp the individual flow rates through the two tubes are given by (Eq. 2.4.3)

q1	=	Δp
			R1
q2	=	Δp		(3.4.1)
			R2

and total flow rate through the system is given by

q = q1 + q2

	R1		+ R2
	=			Δp	(3.4.2)
		R1R2

From these expressions it is clear that if the resistance in one of the two tubes is changed then the flow rate will change in that tube but not in the other. And since total flow rate is the sum of the two then total flow through the system will change too. To illustrate this more clearly, let us consider R2 as being fixed and change the ratio R1/R2. Using Δp and R2 as nondimensionalizing constants, the flow rates can then be put in the following nondimensional forms:

		q1
q1 =
		Δp/R2
=		1		(3.4.3)
		R1/R2

q2 q2 = Δp/R2

= 1

(3.4.4)

q

q = Δp/R2

= 1 +	1	(3.4.5)
	R1/R2

As the ratio R1/R2 changes, these flow rates change as illustrated graphically in Fig. 3.4.2. It is seen that when R1/R2 = 1, flow through each tube has a normalized value of 1.0 and total flow through the system is 2.0. As the value of R1/R2 is decreased from this reference value, flow through R1 is increased

3.4 R1,R2 in Parallel

91

	4
(nondimensionalized)	3.5
	3
	2.5
	2
	1.5			q
rate	1		q2
flow
	0.5		q1
	00	1	2	3	4	5	6
				R1 / R2

Fig. 3.4.2. Normalized flow rates q1, q2 in two resistive tubes in parallel and under a constant driving pressure drop. Total flow rate is q. If R2 is fixed, then a change in the ratio R1/R2 will a ect q1 and q but not q2.

but flow through R2 is unchanged, therefore total flow through the system is increased.

Under the scenario of constant flow rate through the system, writing Eq. 3.4.2 as

R1R2

Δp = q (3.4.6)

R1 + R2

it is clear that a change in any or both of the two resistances will require a commensurate change in Δp in order to maintain the prescribed constant flow rate q. Also, if flow rates are now nondimensionalized in terms of the constant flow rate, we have

q1 q1 = q

=	1	(3.4.7)
	1 + R1/R2

q2 q2 = q

=	R1/R2	(3.4.8)
	1 + R1/R2

92 3 Basic Lumped Elements

(nondimensionalized)	1.2
	1			q
	0.8
				q2
	0.6
rate	0.4
flow	0.2				q1
	00		2	4	6	8	10
					R1 / R2

Fig. 3.4.3. Normalized flow rates q1, q2 in two resistive tubes in parallel and under a condition of constant flow rate q through the system. If R2 is fixed, then a change in the ratio R1/R2 will a ect both q1 and q2 in such a way that total flow through the system (q = q1 + q2) remains unchanged.

q = qq

= 1

(3.4.9)

As before, if R2 is fixed and the ratio R1/R2 is changed, then the change will a ect flow in both tubes in such a way that total flow rate remains constant as prescribed under the present scenario. The results are shown graphically in Fig. 3.4.3.

3.5 R,L in Parallel

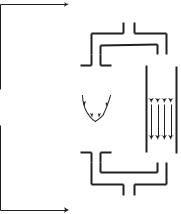
Consider now an element of resistance R and an element of inductance L in parallel under a driving pressure drop Δp as shown in Fig. 3.5.1. Schematically, the two elements in that figure are represented by fully developed Poiseuille flow in one tube, in which the viscous resistance to flow is R, and a hypothetically “ideal” flow in which the viscous resistance is absent but fluid is being accelerated from rest, hence the inertial e ect is present. We shall refer to these briefly as the “resistive tube” and “inductive tube”, respectively.

The pressure drop across the first tube will act to overcome the viscous resistance while across the second tube it will act to accelerate the flow, as

3.5 R,L in Parallel

93

p2

L

p = p2 - p1

R

p1

Fig. 3.5.1. Resistance R and reactance L in parallel, under a pressure drop Δp. Resistance is represented here by fully developed flow in a tube in which the only opposition to flow is the viscous resistance at the tube wall but with no inertial e ect since the flow is fully developed. Reactance is represented schematically by idealized flow in a tube in which the viscous e ect is absent but the fluid is being accelerated from rest, hence the inertial e ect is present.

discussed in more detail in Sections 2.4,5. If the flow rates in the two tubes are denoted by qR and qL, respectively, then these are related to Δp as determined in Sections 2.4,5, namely

Δp = qRR = L

dqL

(3.5.1)

dt

Thus

qR =

Δp

(3.5.2)

R

qL =

1

Δpdt

(3.5.3)

L

and the total flow rate is given by

q = qR + qL

=

Δp

1

(3.5.4)

+

Δpdt

R

L

or

dq

=

1

d(Δp)

+

Δp

(3.5.5)

dt

L

R

dt

If the driving pressure drop Δp is assumed constant, Eq. 3.5.5 reduces to

94	3 Basic Lumped Elements
		dq		=		Δp			(3.5.6)
		dt				L
and its solution is
	q(t) =				Δp		t + A		(3.5.7)
					L

where A is a constant. Also, with Δp constant, Eqs.3.5.2,3 give

qR(t) =	Δp
	R
qL(t) =	Δp	t + B	(3.5.8)
	L

where B is a constant. Since at time t = 0 it is assumed that fluid in the reactance tube is at rest, that is qL(0) = 0, then B = 0 and

qL(t) =				Δp			t		(3.5.9)
				L
The total flow rate through the parallel system is thus given by
q(t) = qR(t) + qL(t)
=	Δp		+			Δp		t	(3.5.10)
	R					L
Comparing Eq. 3.5.7 and Eq. 3.5.10 we see that
A =		Δp							(3.5.11)
			R

and the two equations become identical, as they should. Thus, under the scenario of constant pressure drop, the individual and total flow rates, in nondimensional form, are given by

					(t) =	qR(t)	= 1
	q		R
						Δp/R
					(t) =	qL(t)	=	t
		q	L
						Δp/R	tL
					(t) =	q(t)	= 1 +			t	(3.5.12)
				q
						Δp/R				tL

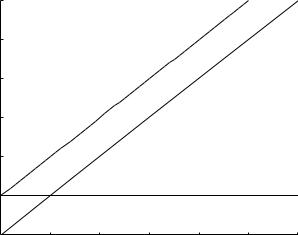
where, as in previous sections, tL = L/R. These are shown graphically in Fig. 3.5.2 from which we see that flow rate through the resistive tube is constant while that through the inductive tube increases linearly and indefinitely with time. The reason for the latter is that in the inductive tube the only

3.5 R,L in Parallel

95

	6
(nondimensionalized)	5				q
	4				qL
	3
	2
rate
flow	1				qR
	00	1	2	3	4	5	6
				t / tL

Fig. 3.5.2. Flow rates qR, qL in a resistive tube and an inductive tube, respectively, in parallel and under a condition of constant pressure drop. Total flow rate is q. In the inductive tube the only opposition to flow is fluid inertia, hence the fluid continues to accelerate under the constant driving force, a scenario which is unrealistic physiologically under normal conditions but may arise under pathological conditions involving a breach in the vascular system through which blood can escape.

opposition to flow is the inertia of the fluid, and in the presence of a constant driving force the fluid continues to accelerate.

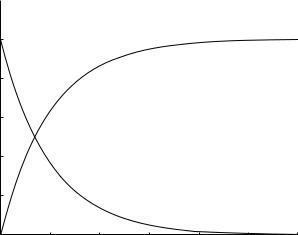
As discussed in the previous section, another scenario of physiological interest is that in which the parallel system in Fig. 3.5.1 is under a condition of constant flow rate rather than constant pressure drop. Thus, setting q constant in Eq. 3.5.5, the equation reduces to

	1 d(Δp)			+	Δp	= 0	(3.5.13)
	R dt				L
with the solution
Δp(t) = Δp(0)e−t/tL							(3.5.14)

where Δp(0) is the value of Δp at time t = 0, which highlights the fact that under the present scenario of constant flow rate the pressure drop driving the flow is not constant. Using this result for the individual flows in Eqs.3.5.2,3, we obtain

96	3 Basic Lumped Elements
	(nondimensionalized)	1			q
		0.8			qL
		0.6
	flow rate	0.4
		0.2			qR
		00		1	2	3	4	5	6
						t / tL

Fig. 3.5.3. Flow rates qR, qL in a resistive tube and an inductive tube, respectively, in parallel and under a condition of constant flow rate q through the system. In the inductive tube the flow rate is increased from an initial value of zero to the value of total flow rate through the parallel system. In the resistive tube there is viscous resistance at any flow rate, thus the flow rate there, starting from total flow rate at time t = 0 (when the inductive flow is zero) drops continuously as time goes on, as more flow, and ultimately all flow, is diverted via the inductive tube.

qR(t) =	Δp(0)	e−t/tL
	R
qL(t) =	Δp(0)		1 − e−t/tL		(3.5.15)
	R

having assumed again that at time t = 0 fluid in the inductive tube is at rest, that is qL(0) = 0. We note that

q(t) = qR(t) + qL(t)
=	Δp(0)	e−t/tL	+	Δp(0)			1 − e−t/tL
	R				R
=	Δp(0)						(3.5.16)
	R

which indicates that total flow rate through the system is constant at all times as it should be (by design) under the present scenario.

Writing these results in nondimensional form, we have

3.6 R,C in Parallel

97

qR(t) qR(t) = Δp(0)/R

= e−t/tL

(3.5.17)

qL(t) qL(t) = Δp(0)/R

= 1 − e−t/tL

(3.5.18)

q(t) q(t) = Δp(0)/R

= 1

(3.5.19)

which are shown graphically in Fig. 3.5.3. We see that as time goes on, under this scenario resistive flow diminishes to zero while inductive flow reaches a constant value equal to total flow. In other words, ultimately the entire flow rate through the parallel system is diverted via the inductive tube. The reason for this, of course, is that in the inductive tube there is no opposition to flow at a constant rate, while in the resistive tube there is viscous resistance at any nonzero flow rate.

3.6 R,C in Parallel

We consider next an element of resistance R and an element of capacitance C in parallel under a driving pressure drop Δp as shown in Fig. 3.6.1, but only briefly, since this configuration was discussed more fully in Section 2.6. Again, the two elements in that figure are represented schematically by fully developed Poiseuille flow in one tube, in which there is viscous resistance to flow, and an expandable “balloon” in which the viscous resistance is absent but a capacitance e ect is present, as discussed at great length in Section 2.6. The pressure drop across the resistance tube will act to overcome the viscous resistance at the tube wall, while across the balloon (p2 inside and p1 outside) it will act to overcome the capacitance e ect of the balloon. More accurately, Δp will act to keep the balloon inflated, and depending on whether and how Δp is changing, it may drive flow into or out of the balloon, as discussed in detail in Section 2.6.

If the flow rate going through the resistance tube is denoted by qR and referred to as “resistive flow”, and that going into the balloon is denoted by qC and referred to as “capacitive flow”, it is important to note that capacitive flow is not a “through-flow” but a flow “into” (or out) of the balloon. The extent of this flow is therefore clearly limited by the capacity of the balloon, that is by the maximum volume to which the balloon can be stretched. Here,