Physics of biomolecules and cells

188	Physics of Bio-Molecules and Cells

Fig. 2.1. Schematic representations of the prototypes of bonding architecture that we consider here. a) Bonds loaded in series. The system fails on breakage of a single bond. b) Bonds loaded in series, but breakage of a bond does not lead to failure of the system (analogy of the unfolding of tandem repeats in multidomain proteins). c) Bonds loaded in parallel. Force is spread evenly across intact bonds. d) A zipper. Bonds are loaded and broken consecutively.

2.2 Impact of cooperativity

We first need to consider the profound impact of cooperativity in multiple bond detachment. By this, we mean some type of strong mechanical coupling exists within a array of bonds that only allows the molecules to pass transition states synchronously. Even though atomic scale excitations remain uncorrelated in time, sti mechanical coupling can create collective modes on long length scales that lead to strong correlations on the time scale for overdamped relaxation of the complex. Such a system behaves like a macro-single bond with a barrier given by the sum of the individual barrier energies. But quite di erent outcomes arise for the series and parallel loading arrangements shown in Figure 2.1. For a simple-ideal bond, we have seen that the lifetime is set by the exponential magnitude of the energy barrier with a di usive relaxation time as the prefactor,

to = tD exp(Eb/kBT ).

(2.1)

With N -identical bonds, cooperative unbinding leads to an enormous increase in the time scale for dissociation as approximated by

to (N ) ≈ N to exp[(N − 1)Eb/kBT ].

(2.2)

E. Evans and P. Williams : Dynamic Force Spectroscopy

189

Fig. 2.2. A system of identical attachments that fail cooperatively when loaded in parallel can be considered as a single bond with a N -fold increase in the barrier compared to a single bond. The force scale of the compound bond remains the same as for a single bond interaction.

(Note: The prefactor N is based on the assumption that molecular damping scales with N .) For identical-cooperative bonds in parallel (cf. Fig. 2.2), location of the transition state xβ and thermal force scale fβ = kBT /xβ remain that for the single bond (see Part I for more details). Hence, the unbinding rate under force f is,

ν→(N ) ≈ [1/to (N )] exp(f /fβ ).

(2.3)

For identical bonds in series, each bond contributes an increment in length along the direction of force on unbinding and thus the thermal force scale is lowered N fold, i.e. fβ /N . Hence, the unbinding rate for cooperative bond

190	Physics of Bio-Molecules and Cells

Fig. 2.3. A system of identical attachments that fail cooperatively when loaded in series can be considered as a single bond with both a barrier and force scale N -times that of the single bond. The increase in force scale makes the series connection weaker under force than the parallel system.

in series,

ν→(N ) ≈ [1/to (N )] exp(N f /fβ )

(2.4)

increases exponentially faster with force than for bonds in parallel. Based on the generic relation for most frequent rupture force f (defined by, 1/rf = −[∂(1/ν→)/∂f ]f =f , from Eq. (1.34) in Part I), equations (2.3) and (2.4) show that it takes much less force for cooperative failure of bonds in series,

f ≈ (fβ /N )[log(rf ) + 2 log(N ) + (N − 1)Eb/kBT ]	(2.5)
than for bonds in parallel, i.e.
f ≈ fβ [log(rf ) + log(N ) + (N − 1)Eb/kBT ]	(2.6)

when either is broken far from equilibrium.

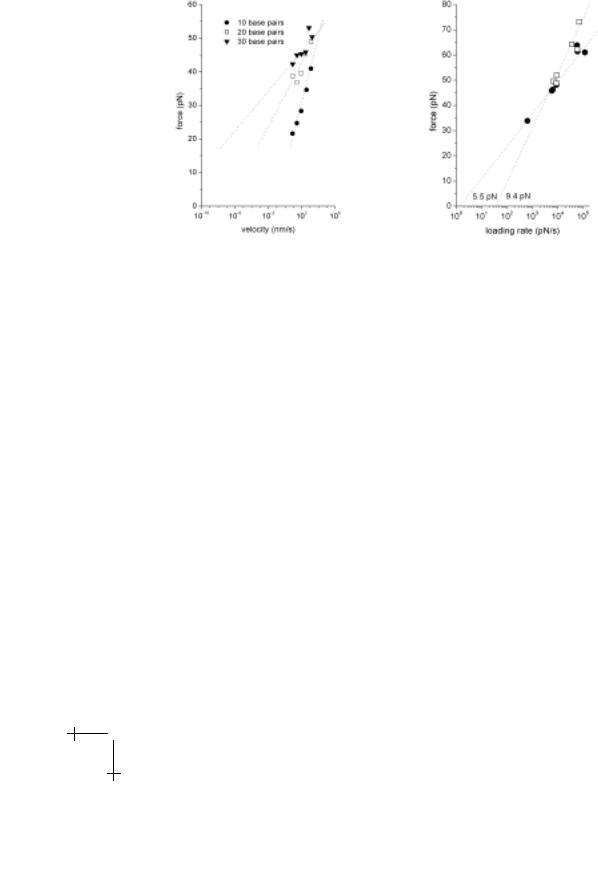
As shown in Figure 2.4, cooperative failure of multiple bonds has been observed in DFS studies of short strands of DNA (oligonucleotides) using the atomic force microscope (AFM). The DNA double helix is held together by the predominately hydrogen-bonding interaction of nucleotides along the strands. Each interaction accounts for a few kBT of energy and the extrapolated dissociation rate appears to increase exponentially with the number of base pairs. Hence, increasing the number of base pairs from 10 to 30 leads to an increase in the lifetime of the duplex from several seconds to many years! Interestingly, recent experiments with RNA (to be published) show

E. Evans and P. Williams : Dynamic Force Spectroscopy

191

Fig. 2.4. Left: DFS study of the rupture of oligonucleotide strands of 10, 20 and 30 base-pair length behaves like cooperative failure of bonds in series (taken from Strunz et al.). The force scale diminishes with increase in length and is approximated by (35/N) pN. The extrapolated o -rate increases exponentially with increasing length. Right: DFS study of RNA duplexes. 12 base pairs produces a force scale of 5.5 pN. It appears that insertion of a 3-base bulge along one of the strands apparently disrupts the cooperativity and e ectively doubles the force scale to 9.4 pN.

identical results but addition of a bulge at the mid-point of the duplex disrupts cooperativity and increases of the force scale. Thus, this type of design could be of use to probe the origin of cooperative unbinding.

2.3 Uncorrelated failure of bonds loaded in series

2.3.1 Markov sequence of random failures

Given the soft compliance of most molecular interfaces in liquids, there is no reason a priori to expect multiple bonds holding two surfaces together to act cooperatively or pass transition states coincidently in time. For example, several selectin interactions hold a white blood cell to an endothelial wall under strong hydrodynamic loading. Whilst each selectin bond is made up of several widely separated atomic scale interactions that may unbind coincidently, there will be no coincidence between detachment at the di erent selectin sites even though the rupture event may occur extremely rapidly. Uncorrelated failure of multiply-bonded attachments is distinctly di erent from that of the cooperative case described in Section 2.2. Like the evolution

192	Physics of Bio-Molecules and Cells

of states in a complex bond (see Sect. 1.3.3 in Part I), the state of bonding amongst multiple bonds in an attachment is treated as a Markov sequence where a hierarchy of master equations predicts the survival of the attachments as a function of time. In the examples to follow, we will consider multiples of simple bonds with a single transition state but will note the approach to treating multiples of complex interactions with additional-inner transition states. The master equations for unbonding a multiple bonds are identical to those in Table 1.1 of Part I except the “level” in an energy landscape is replaced by the number of bonds that remain during the time course of detachment. (Note: for obvious reasons, we will define the system hierarchy so that subscript “u” represents the unbonded state and that “n” represents the transient n-bonded attachment where n = 1 → N .) Temporal evolution of the N -bonded state commences with the rate at which N bonds decrease to N − 1 diminished by the rate at which N − 1 increase to N ,

dSN /dt = −νN →N −1SN (t) + νN ←N −1SN −1(t) and sequentially through intermediate states according to,

dSn/dt = −[νn→n−1 + νn+1←n]Sn(t) + νn+1→n Sn+1(t) + νn←n−1Sn−1(t) ending with complete detachment,

dSu/dt = −ν1←uSu(t) + ν1→uS1(t).

Here unbonding νn→n−1 and rebinding νn←n−1 rates reflect the rates for rupture or formation between populations of “n” and “n − 1” bonds, which will depend on the type of architecture and mechanics of loading bonds in the multiple attachment. Again for simplicity, we will base our discussion on the behaviour of identical bonds, each of which has an unbonding rate under force given by to ν→ = exp(f /fβ ), and assume that under rapid rise in force, detachment occurs far from equilibrium at each step (i.e., ν← 0). Hence, under a force ramp, rf = df /dt, the master equations reduce to,

N bonds

dSN /df ≈ −(1/rf ) νN →N −1(N, f ) SN (f )

.

.

dSn /df ≈ −(1/rf ) νn→n−1(n, f ) Sn(f ) + (1/rf ) νn+1→n(n + 1, f ) Sn+1(f ) (2.7)

.

.

complete detachment

dSu/df ≈ (1/rf ) ν1→u(1, f ) S1(f )

E. Evans and P. Williams : Dynamic Force Spectroscopy

193

where, in general, the rate of transition νn→n−1(n, f ) at any step of detachment can depend on existing number “n” of bonds as well as force. For instance, the statistical rate of failure of “n” equivalent bonds is n-fold that of a single bond, irrespective of the system architecture and loading dynamics. When breakage of one bond does not lead to failure of the attachment, it is essential to specify the manner in which the force is redistributed amongst the remaining bonds.

2.3.2 Multiple-complex bonds

As a footnote to Section 2.3.1 above, the situation becomes much more complicated when the attachments are formed by complex bonds with several levels and transition states. For a multiple attachment of N identical complex bonds, each with M levels (local energy minima) and intervening barriers, evolution of the system involves N × M master equations where survival of the n-bonded state is governed by transport of states between the interior m levels until an unbinding event. Thus, a matrix of functions

Sn,m(t) is needed to describe the likelihood of being in the mth level of the n-bonded state. Even when each bond rupture occurs with no chance of

rebinding, the internal states of complex bonds may still undergo forward and reverse transitions past interior barriers. So for example, steady loading and rupture of N -identical bonds with two transition states are modelled by the following hierarchy,

N bonds

dSN,1/df = −(1/rf ) ν1→2(N, f ) SN,1(f ) + (1/rf ) ν1←2(N, f ) SN,2(f ) dSN,2/df = −(1/rf ) [ν2→u(N, f ) + ν1←2(N, f )] SN,2(f )

+ (1/rf ) ν1→2(N, f ) SN,1(f )

.

.

dSn,1/df = −(1/rf ) ν1→2(n, f ) Sn,1(f ) + (1/rf ) [ν2→u(n + 1, f ) Sn+1,2(f ) + ν1←2(n, f ) Sn,2(f )]

dSn,2/df = −(1/rf ) [ν2→u(n, f ) + ν1←2(n, f )] Sn,2(f )

+ (1/rf ) ν1→2(n, f ) Sn,1(f )

.

.

dS1,1/df = −(1/rf ) ν1→2(1, f ) S1,1(f ) + (1/rf ) [ν2→u(2, f ) S2,2(f ) + ν1←2(1, f ) S1,2(f )]

194	Physics of Bio-Molecules and Cells

dS1,2/df = −(1/rf ) [ν2→u(1, f ) S1,2(f ) + ν1←2(1, f ) S1,2(f )] + (1/rf ) ν1→2(1, f ) S1,1(f )

complete detachment

dSu/df = (1/rf ) ν2→u(1, f ) S1,2(f ).

Again at any stage of detachment, the rates of transition can depend on existing number “n” of bonds as well as force and passage of the final transition state ν2→u(n, f ) is assumed to be terminal for each state of bonding, i.e. ν2←u(n, f ) = 0. Clearly, solving such a system of master equations for many attachments demands tedious numerical computation. But as described Part I, useful analytic approximations (Eqs. (1.18) and (1.19) of Part I) exist for multiple bond attachments which will prescribe e ective rates νn→n−1(f ) for transition of the n-bonded state to n −1 bonds over the course to complete failure. We introduce these approximations where appropriate in our discussion of the di erent bonding architectures illustrated in Figure 2.1.

2.3.3 Multiple-ideal bonds

Beginning with a chain of identical bonds, each bond experiences the same force but the rate of transition from N to N − 1 bonds is proportional to the number of bonds in the chain, to νN →N −1 = N exp(f /fβ ). If an unbinding event breaks the chain, the probability density for failure or force distribution pN (f ) follows from a single master equation:

dSN /df = −(1/rf )(N/to ) exp(f /fβ ) SN (f ) = −pN (f ).

This simply rescales the loading rate to give pN (f ) = N exp{f /fβ − N fβ [exp(f /fβ ) − 1]/(rf to )}/(rf to ) and introduces a log(N ) weakening of the most frequent force for failure, f = fβ [log(rf to /fβ ) − log(N )]. By comparison, a series of bonded “knots” (like folded Ig domains of a long titin protein) behave di erently in that the chain does not fail with an unbonding event. There is an quick drop in force to a new level which arises from the length of unfolded protein inserted in the chain. The system re-equilibrates and the random process “clock” is reset. Force again increases although from a level which is not necessarily zero. Also, as discussed previously in Section 1.4.5 of Part I, adding a large length of unfolded material into the chain can have an important impact on the loading rate. For unravelling a series of knots, therefore, rupture events become separated in time and produce a “saw-tooth pattern” of force with very nonlinear loading characteristics. Each of these force “spikes” can be considered as a distinct test of the knot-bond strength amongst the n remaining knots under anharmonic loading conditions.

E. Evans and P. Williams : Dynamic Force Spectroscopy

195

By comparison, there is little drop in force on breakage of a bond in the case of a zipper (peeling a sequence of bonds). Nearly the same level of force is transferred to the next bond and so on. Again, there are N independent tests of bond strength but starting at randomly-distributed initial loads. Assuming identical bonds under steady loading, the rate of failure for each bond has the same dependence on force and force is proportional to time. Thus, evolution of a zipper can be modelled by the following master equations,

N bonds

dSN /df = −1/(rf to ) exp(f /fβ ) SN (f )

.

.

dSn/df = −1/(rf to ) exp(f /fβ ) Sn(f ) + 1/(rf to ) exp(f /fβ ) Sn+1(f )

.

.

complete detachment

dSu/df = 1/(rf to ) exp(f /fβ ) S1(f ) = pN (f ).

Somewhat more complicated than simultaneously pulling on a series of bonds, the master equations can still be integrated to find the probability density pN (f ) for final detachment of a zipper with N identical bonds. A simple transformation of variables, u ≡ fβ [exp(f /fβ ) − 1]/(rf to ), leads to the Poisson-like result,

pN (f ) uN −1 exp(−u) du/df = {fβ [exp(f /fβ ) − 1]/(rf to )}N −1 p1(f )

where p1(f ) = exp{f /fβ − fβ [exp(f /fβ ) − 1]/(rf to )}/(rf to ) is the probability density for failure of the one bond. As shown below in Figure 2.5, a

zipper of bonds results in a log(N ) strengthening of the most frequent force for complete detachment.

2.3.4 Equivalent single-bond approximation

Although often necessary, solving the system of master equations for mul- tiple-bond attachments is clearly time consuming and requires detailed definitions of many molecular scale parameters. Thus, as for a complex-single bond described in Section 1.4.6 of Part I, we employ analytic approximations for e ective rate of unbinding ν→ in a multilevel system to collapse the master equations for complete detachment of multiple bonds to a rate of failure νN → for an “equivalent single bond”. In this way, the most frequent

196	Physics of Bio-Molecules and Cells

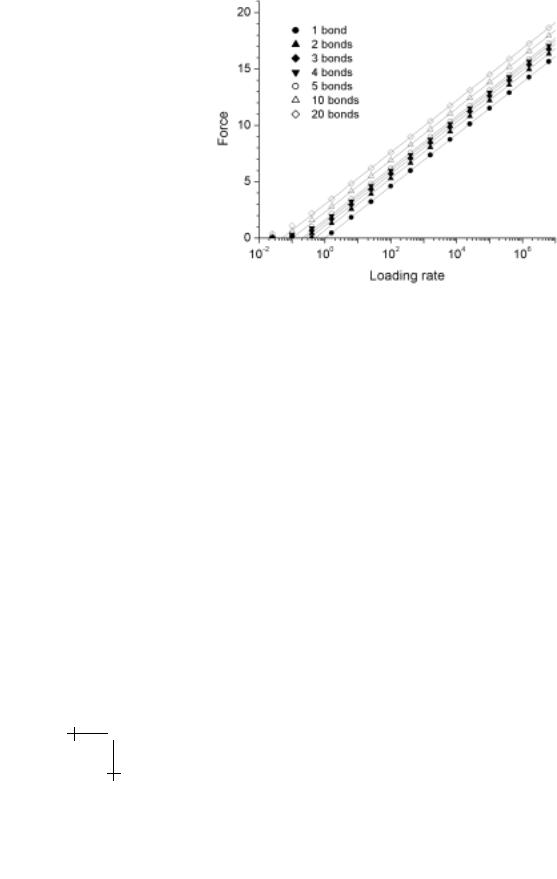
Fig. 2.5. Rupture forces (scaled by fβ ) found by solution to the master equations (symbols) for a zipper of between 2 and 20 bonds. (Loading rate is scaled by fβ /to .) Also shown by solid lines are the forces predicted by the equivalent single attachment model, which closely match the computational results at forces f /fβ > 1.

rupture force or strength of a multibond attachment f can be easily estimated using the generic expression for location of the peak (at ∂pN /∂f = 0) in the probability density for failure of the equivalent single bond (Eq. (1.33) in Part I),

1/rf = −[∂(1/νN →)/∂f ]f =f .

(2.8)

The case of N -identical simple bonds in series (Fig. 2.1a) is trivial. Here, each bond experiences the same force history and any rupture event leads to failure of the attachment. Thus, the rate of failure events is N -fold faster than the rate for one bond (as any one of the N may break). Because of the N -fold scaling of rate, it follows from equation (2.8) that the attachment is weakened slightly as demonstrated earlier, f = fβ [log(rf to /fβ ) −log(N )], compared to a single bond at the same loading rate.

Serial linkages of dissimilar bonds are, however, more subtle. We expect rupture to occur at the weakest bond and naively also expect that strong versus weak should follow the scale set by the energy barriers sustaining the bonds. But surprisingly, thermal force scales for

E. Evans and P. Williams : Dynamic Force Spectroscopy

197

exponentiation of unbinding rates are also important factors in the determination of strong versus weak. This follows from the failure rate defined by the sum of the unbinding rates for each bond. Taking properties (to or Eb, and fβ ) of the bond with the smaller barrier energy for a reference, the combined rate of failure of two bonds in series can be expressed

as, to ν→ ≈ exp(f /fβ ){1 + exp[−∆Eb/kBT + f ∆(1/fβ )]}; ∆Eb > 0 and ∆(1/fβ ) are the di erences in barrier energy and rate-exponentiation scale

of the bond with a higher barrier. Based on the combined rate of failure, the bond with the smaller energy barrier remains the weak bond so long as the inequality, ∆Eb/kBT > f ∆(1/fβ ) holds. However, if the bond with a higher barrier has a greater amplification of rate under force or smaller force scale (i.e., ∆(1/fβ ) > 0), a crossover, ∆Eb/kBT < f ∆(1/fβ ), will occur as the force is increased. Beyond the crossover, the bond with the higher barrier will become the most likely site of failure (i.e., the weak bond). Thus, in a DFS spectrum, an abrupt reduction of slope from a linear regime at low loading rates to the next regime at higher rates signals a switch in site of failure amongst bonds in a series linkage.

In zipper-like failure (Fig. 2.1d), bonds break in sequence but at random times from first to last. Hence, far from equilibrium, the failure of the nth bonded state to n−1 attachments proceeds at a common rate, νn→n−1(f ) = (1/to ) exp(f /fβ ), so given N identical bonds, the approximate rate for breaking all bonds is essentially the reciprocal of the sum of times to break each bond,

1/νN →(f ) = to Σ1→N exp(−f /fβ ) = N to exp(−f /fβ ). (2.9)

Thus, the e ective loading rate for the equivalent single-bond attachment is diminished by N fold and equation (2.8) shows that final separation of a zipper of identical bonds requires a slightly larger force than one bond (see Fig. 2.5),

f ≈ fβ [log(rf to /fβ ) + log(N )].

(2.10)

This approximation is easily verified by calculation of the peak (at ∂pN/∂f = 0) of the zipper probability density described in the previous section. For comparison, imagine that each unbinding event was punctuated by force drops to zero and that the loading rate remained constant. Then, the time needed to unzip N bonds would be nearly N -fold longer, i.e. ΣN f (1)/rf = N (fβ /rf ) log(rf to /fβ ). But when force propagates instantly from one bond to the next, the time for complete detachment is only slightly longer than needed to break a single bond, f (1)/rf + (fβ /rf ) log(N ).