Physics of biomolecules and cells

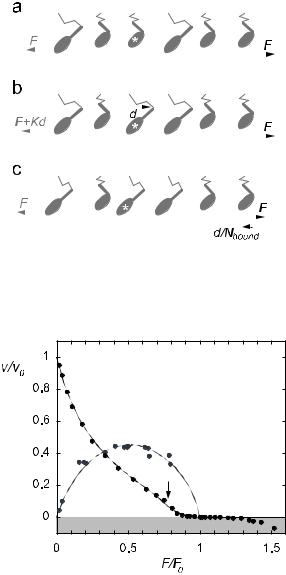
T. Duke: Modelling Motor Protein Systems

117

Fig. 12. a) In mechanical equibrium, the sum of the forces exerted by the motors (grey arrow) opposes the applied load (black arrow). b) If one of the motors binds and undergoes its power-stroke, the force balance is momentarily upset. c) As a consequence, the filaments slide to restore mechanical equilibrium.

Fig. 13. Force-velocity relation (black) and e ciency (grey) of muscle. Experimental data (points) are compared with model predictions (lines).

force-velocity relation of single muscle fibres [46]. In the model, it is caused by the inhibition of the power-stroke at high loads. As already mentioned,

118	Physics of Bio-Molecules and Cells

when 12 Kd2 slightly exceeds ∆µPi , a motor needs the assistance of its team mates to e ect its power-stroke. Close to isometric conditions, the other motors do not advance the filament rapidly enough to help, and sliding breaks down. At still higher loads, almost no power-stroke transitions can occur and the myosin heads simply bind and detach reversibly, without releasing the products of hydrolysis. In doing so they create a high protein friction, so the filaments slide backwards (corresponding to muscle extension) only slowly. This suggest another reason why a strong elastic element may be favourable. It permits the muscle to support a variety of high loads while remaining at an almost constant length and without expending much energy.

2.7 Dynamical instability and biochemical synchronization

The abrupt decline of sliding velocity at high loads actually corresponds to a sudden change of dynamical behaviour. As shown in Figure 14, the filaments no longer slide smoothly at a constant velocity, but move in a stepwise fashion [33]. The transition is a direct consequence of the fact that myosin heads must cooperate with one another in order to execute their power-strokes. At zero load, they are able to do so in an uncorrelated way, with individual molecules binding and detaching at random intervals. Those heads which have been bound for the longest period of time get dragged into a position in which they exert negative force. This balances the positive force exerted by the heads that have just executed their power-stroke. Because of the

Fig. 14. At high load, the dynamics changes from smooth sliding to stepwise motion.

T. Duke: Modelling Motor Protein Systems

119

strain-dependence of ADP release, it is the former subset of heads that has the highest instantaneous detachment rate. Their continual dissociation causes the thin filament to advance su ciently rapidly to ensure that any newly bound heads are always able to execute their power-stroke. Consequently, the sliding is smooth. As the load is raised and the average sliding velocity diminishes, this situation breaks down. The power-stroke transitions of individual motors begin to fail. Nevertheless, if an individual head does succeed in accomplishing a power-stroke, it causes the thin filament to advance by a small amount and reduces the strain of all the other attached heads, thereby facilitating their own power-stroke transitions. Owing to this cooperativity, a large fraction of the bound heads can stroke almost simultaneously, like a rowing crew, causing the thin filament to lurch forward through a distance approximately equal to the length of the power-stroke. Subsequently, the heads detach stochastically and they must rebind in sufficient numbers to be able to coordinate another cascade of power-stroke transitions. Thus the dynamics is quasi-periodic, with a period defined by the cycle time of an individual molecule. This suggests that the isometric condition of muscle may not be a steady state, but rather one in which some sarcomeres are lengthening and others are shortening at any instant of time.

2.8 Transient response of muscle

There is one experiment in which the absence of a steady state in nearisometric conditions would have a clear, observable consequence: the isotonic transient response, in which an isometric muscle fibre is subjected to a sudden decrease in load. The external mechanical stimulus would synchronise the power-stroke transitions of the bound myosin heads throughout the filament. Subsequently, individual sarcomeres would start to shorten in a stepwise fashion but, owing to filament compliance, the coordination of different sarcomeres would gradually be lost. The consequence would be an apparent, damped oscillatory motion of the fibre. This is precisely what is observed in muscle [47, 48].

3 Motors at work: Collective properties of motor proteins

3.1 Dynamical instabilities

One of the fundamental lessons of statistical physics has been that even a very simple system, composed of identical elements with pairwise interactions, can display emergent collective properties. An example is the abrupt condensation of a gas as the temperature falls below a critical value. Such

120	Physics of Bio-Molecules and Cells

phase transitions, in which one type of collective behaviour becomes unstable and another comportment is favoured, are a consequence of cooperativity in the microscopic interactions. A system in which many motor proteins act collectively is considerably more complex than a gas, because the individual entities are not just passive molecules, but active force generators. A collection of motors is a non-equilibrium system, but by analogy with a thermodynamic system we should expect the cooperativity (which is due to mechano-chemical coupling) to induce dynamical instabilities. The transion from smooth sliding to stepwise motion, discussed in the previous section, is one example. In order to explore other examples, we will return to the isothermal ratchet model, whose simple formulation facilitates the analysis of collective e ects.

3.2 Bidirectional movement

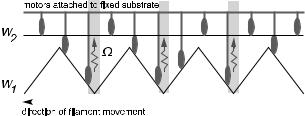
In Section 2, we saw that an individual motor can move unidirectionally along a polar filament, and that its direction of motion is determined by the form of the interaction potentials and by the position dependence of the transition rates between di erent motor states. When a number of motors act together to propel a filament, however, the direction of motion is a team property. The filament might move in either sense, and, in some cases, it might be able to move in both directions [49]. To see how such bidirectionality can arise, it is easiest to consider the hypothetical case of a non-polar filament. The absence of asymmetry in the potentials means that an individual motor is incapable of moving directionally. But as shown in Figure 15, multiple motors can propel a filament in either direction if the reaction rates are strain-dependent, such that detachment can only take place at a localized position near the bottom of a potential well. Suppose that the motors are driving the filament to the left. Then, owing to the detachment of motors which have recently passed through a potential well, there are more bound motors on the right-facing slope of the potential

Fig. 15. A team of motors can propel a filament, even if the interaction between an individual motor and the filament is symmetric.

T. Duke: Modelling Motor Protein Systems

121

than on the left-facing slope (as shown). Sliding down the slope, these motors produce a force which sustains the filament’s leftward movement. An equivalent argument shows that the filament could just as well be driven to the right.

Thus, there are situations in which a team of motors can drive a filament either forwards or backwards. A filament would not travel one way for an indefinite period, however. Stochastic fluctuations in the numbers of motors pushing and pulling would eventually cause an abrupt switch to the alternative steady-state solution [50]. Interestingly, such behaviour has recently been seen in a motility assay, in which the motion of microtubles was observed as they glided over a lawn of Ncd motors absorbed on a surface [51]. Typically, an individual microtubule travelled for several micrometers with its plus end leading, then abruptly reversed direction and travelled for a similar distance in the opposite sense. The speed was approximately the same in each direction and the reversals appeared to occur quite randomly. The particular Ncd molecule used was a mutant with a single amino-acid substitution in the neck region, which links the heads to the coiled-coil tail. The ratchet model suggests that this mutation modifies the e ective interaction potential of the motor with the microtubule, so that it is almost symmetric despite the microtubule’s polarity.

3.3 Critical behaviour

The collective property of bidirectional motion arises because, when a number of motors are pulling one way, they enhance the likelihood that their teammates will join in and pull in the same direction. This only happens, however, only if the rate of stimulated detachment is faster than a critical value. The system has to be su ciently far from equilibrium (which means, in practice, that the concentration of ATP has to be above a critical level).

This critical behaviour may be analysed using a simple model 2-state isothermal ratchet model [12, 49], writing the transition rates as

ω21 = α
ω12(x) = α e(W1 −W2)/kT + Ω(x).	(3.1)

Here Ω(x) is the rate of non-thermal transitions from the bound state; it represents detachment stimulated by chemical reactions, and its value characterizes how far the system is from equilibrium. If the motors and the filament are moving with respect to one other at relative velocity v, the probabilities of occupancy of either state satisfy

∂t P1 + v∂xP1 = −ω12(x)P1 + ω21(x)P2
∂t P2 + v∂xP2 = ω12(x)P1 − ω21(x)P2	(3.2)

122	Physics of Bio-Molecules and Cells

Fig. 16. Force-velocity relation for a team of motors interacting with a symmetric filament.

and P1 + P2 = 1 gives

v∂xP1 = − [ω12(x) + ω21(x)] P1 + ω21(x) .

(3.3)

If the motion is opposed by an external load F , the equation for the balance of forces is

a

N dxP1 ∂xW1 = F + ζv (3.4)

0

where the expression on the left hand side is the active force generated by the motors. Equations (3.3) and (3.4) together specify the force-velocity relation. At low velocities the relation may be written as an expansion which, for the case of the symmetric system discussed above, contains only odd terms

F = −ζv + A(Ω)v + B(Ω)v3 + ...

(3.5)

The force-velocity relation is shown in Figure 16 for di erent values of Ω. At equilbrium, Ω = 0, the cubic coe cient vanishes, B(0) = 0, and the linear

coe cient is negative, representing the protein friction: −A(0) = ζprotein. Thus the filament simply slides passively backwards, as expected

v(Ω = 0) = −	F	·	(3.6)
	ζ + ζprotein

T. Duke: Modelling Motor Protein Systems

123

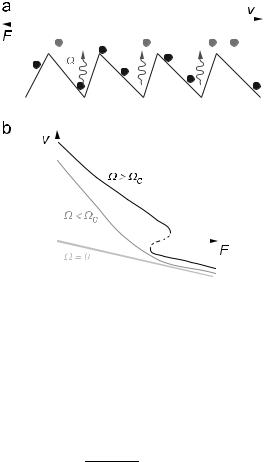
Fig. 17. a) Team of motors interacting with a polar filament. b) Possible forcevelocity relation.

However, when the system is out of equilibrium, the linear coe cient A can become positive; and above a critical value of the stimulated detachment rate, it can exceed the viscous drag coe cient. Thus, for Ω > ΩC, given by A(ΩC) = ζ, equation (3.5) can have a non-zero solution for v in the absence of an applied load F . Spontaneous motion occurs with velocity

			±	A(Ω) − ζ		1/2
	v	(Ω) =					(Ω	−	Ω	)1/2.	(3.7)
				B(Ω)
	±								c

In the vicinity of the critical point, the behaviour is generic and the velocity obeys characteristic power-law relations. For example, when a load is applied, the velocity varies as

v(Ωc) −F 1/3.

(3.8)

Although the occurrence of bidirectionality is especially easy to illustrate for the case of a symmetric ratchet, it is not confined to this situation but is also likely to occur under certain load conditions in asymmetric ratchets [12,49]. A typical case is shown in Figure 17. Crossbridge models can also display regimes in which multiple motors can drive a filament both forwards and backwards [34]. Thus bidirectional motion may be common in naturally occurring motor protein systems, and not just a property of unusual mutants.

124	Physics of Bio-Molecules and Cells

Indeed, bidirectional motion was first reported in an actomyosin motility assay [52].

3.4 Oscillations

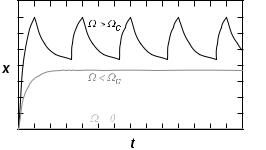
A region of hysteresis in the force-velocity diagram of the type shown in Figure 17 has an interesting implication: if the filament is connected in series with an elastic element, it will oscillate [53]. The motors first drive the filament forwards and as the spring stretches, the increasing load slows the movement down. But before the filament comes to a halt, the forward motion becomes unstable and the system jumps to the other stable branch, for which the velocity is negative. Consequently the motors start to drive the filament backwards. As they do so, the tension in the spring declines and thus so does the speed. But again, before the filament stops, the motion becomes unstable and the system abruptly jumps back to the original branch. As shown in Figure 18 these motor-driven oscillations have a characteristic saw-tooth form. In general, the amplitude of oscillation depends on the degree of hysteresis, which itself depends on the amount by which Ω exceeds ΩC.

Fig. 18. Oscillations induced by a team of motors in series with a spring.

The critical point Ω = ΩC corresponds to a Hopf bifurcation [53]. It is at this point that sinusoidal oscillations with vanishing amplitude, but a welldefined frequency, set in. Their characteristic frequency

ωc	α ζ			1/2
				(3.9)
		K

is the geometric mean of two rates: the typical kinetic rate of the motor α;

and the rate of viscous relaxation of the filament 1/τvisc = K/ζ. Interestingly, the frequency of oscillation can be significantly faster than the cycle

T. Duke: Modelling Motor Protein Systems

125

time of an individual motor. There is, however, an upper limit to the frequency, since the dynamical instability is eliminated if the external spring is stonger than the total e ective elasticity of the motor crossbridges (the elastic constant kxb of a single crossbridge may be estimated in the ratchet model as kxb = U/l2, where U is the height of the potential maximum and l is the period). Thus the maximum attainable frequency is [54]

ωc α N	k		1/2
			·
	ζxb			(3.10)

There are a number of natural motor systems which oscillate. The vibration of insect flight muscle is too rapid to be controlled by nervous impulses on a cycle-by-cycle basis [55], and is thought to be generated by a dynamical instability of the actomyosin system, which might be based on the type of mechanism described here. Normal striated muscle, in unusual chemical conditions of elevated ADP concentration, also displays large scale oscillations with a characteristic saw-tooth profile [56, 57]. Of special interest, however, is the undulation of spermatazoid flagella, which might be caused by an oscillatory instability of teams of axonemal dynein motors. Before examining this possibility, we shall investigate how the force generated by motor proteins can be used to bend cytoskeletal filaments and generate dynamical patterns.

3.5 Dynamic buckling instability

In a gliding motility assay, fluorescently-stained cytoskeletal filaments are observed as they move across a surface on which motor proteins have been absorbed. The filaments usually glide smoothly, but occasionally they encounter defects, which pin them at their leading end [58]. As shown in Figure 19, the filaments then move in an intriguing way: they either whirl around in a spiral, or they writhe like a snake. These two patterns of behaviour are a consequence of a buckling instability, caused by the force that the motors generate along the contour of the filament. Despite the microscopic size of the system, the dynamics can be treated using continuum elasticity theory [58]. In a standard buckling instability (such as that which occurs when a flag-pole is built too tall) the system comes to a new mechanical equilibrium. In the case of the gliding assay, however, the direction of the applied force changes as the filament bends. As a result, the system evolves to a limit-cycle, instead of a fixed point.

Describing the instantaneous configuration of the filament by the curve r˜(s), and writing the gradient of the curve u˜ = ∂sr˜, the equation of motion of the filament is

ζ∂t r˜ = f u˜ + κ∂s3u˜ + T ∂su˜.

(3.11)

126	Physics of Bio-Molecules and Cells

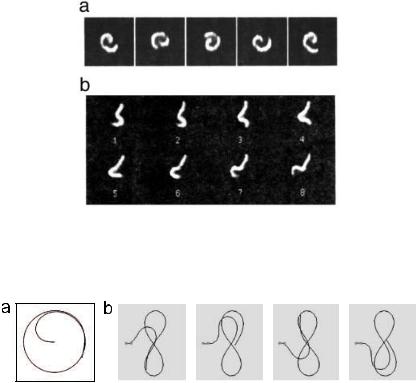
Fig. 19. Dynamical behaviour of cytoskeletal filaments which have been momentarily pinned in motility assays. a) Spiral motion. b) Undulation reminiscent of a flagellum.

Fig. 20. Dynamic buckling instabilities. a) Spiral motion of a filament pinned at one end. b) Figure-of-eight motion of a filament pinned at two positions.

Here, f is the force per unit length that the motors exert along the filament contour, and κ is the bending modulus of the filament. The action of the motors additionaly gives rise to an internal compressive thrust T in the filament, which can be determined by imposing the constraint of fixed contour length. This equation must be supplemented with appropriate boundary conditions.

If the position of the leading end is fixed, but the filament is free to swivel about this point, the asymptotic solution is a spinning spiral pattern, shown in Figure 20a. A simple scaling argument reveals how the radius R of the spiral varies with the driving force per unit length. On the limiting circle, the bending moment is M = κ/R. In the steady state, this must be equal to the torque Γ produced by the external forces (the motor force and the friction). Since the radius of the spiral is the only relevant length scale,