Physics of biomolecules and cells

MODELLING MOTOR PROTEIN SYSTEMS

T. Duke

Abstract

Motor proteins are the cell’s workforce. They are specialized molecules which convert chemical energy to mechanical work, thereby generating force and directional motion. In some situations motor proteins act individually, but more commonly they cooperate in large ensembles to accomplish cellular functions. How do molecular motors work? And how do they work together? This lecture course recounts theoretical approaches to these questions, which complement the experimental investigations of motor protein systems described in Jonathon Howard’s course. The methods of non-equilibrium statistical mechanics permit a general analysis of how chemical energy can most e ectively be used to generate the movement of an individual motor. The class of models known as “isothermal ratchets”, in particular, is a powerful tool for discussing the principles of energy transduction. More specific kinetic models, such as the “swinging lever-arm” model which is based on the known structure and chemistry of the myosin protein, indicate how these molecules are designed to work e ciently together to drive the contraction of muscle. Both classes of model indicate what types of collective e ects can arise when many molecules operate in concert. Cooperative interactions within a team of motor proteins may lead to dynamical instabilities and hysteretic behaviour, which can be exploited to generate oscillations. Physiological processes which may rely on such instabilities include the vibration of insect flight muscle and the undulation of spermatozoid flagella. Motor proteins also play functional roles in sensory systems – hearing being a particularly intriguing example. Hair bundles, which are the mechano-sensors that detect motion in the inner ear, have been found to vibrate spontaneously. Motor proteins appear to play a role either in generating the oscillations, or in maintaining the bundles at the threshold of the oscillatory instability. Poised on the verge of vibrating, they are especially responsive to faint sounds.

c EDP Sciences, Springer-Verlag 2002

98	Physics of Bio-Molecules and Cells

1 Making a move: Principles of energy transduction

1.1 Motor proteins and Carnot engines

Molecular motors’ principal role in biological cells is the generation of force and motion [1–4]. The basis of their function is thus the transduction of chemical energy to mechanical work. When trying to understand how this is achieved, the most important consideration to bear in mind is the tiny size of these molecular machines. Motor proteins live in the Brownian domain [5–14]. Their operation is based on individual chemical reactions, which are accompanied by energy changes that do not greatly exceed the thermal energy. As a result, they function in a highly stochastic way. The consequences are strange. For example, motor proteins cannot be held still in one place, owing to the continual bombardment by molecules in the surrounding solution. Conversely, molecular motors cannot exert a sustained force without the continual consumption of chemical energy.

In this unfamiliar Brownian realm, our knowledge of how macroscopic engines work, based on the laws of classical thermodynamics, is of little help. Molecular motors are not miniature Carnot engines [8, 12]. Nevertheless, the microscopic model of a Carnot engine invented by Feynman [15] serves as a useful starting point, because it introduces the notion of a microscopic ratchet. In our everyday experience, ratchets are devices that are used to rectify motion – to ensure that movement in one sense is permitted and motion in the opposite sense is denied. Feynman asked whether such a device, contructed on the microscopic scale, could be used to rectify the fluctuations caused by Brownian motion. His machine consisted of a rotating vein connected to a cogwheel with saw-teeth, whose movement was restricted by a pawl. He demonstrated that the random percussion of molecules on the vein could drive the cog round, but only on one condition: the cog must be enveloped by molecules at a di erent temperature to those surrounding the vein. Feynman’s thermal ratchet operates exactly like a Carnot engine. It can convert heat to mechanical work provided that a di erence in temperature between cog and vein is maintained. Might a motor protein function the same way? Could a molecular motor use an exothermic chemical reaction to produce heat and raise the temperature of the surroundings, and then use the di erence in temperature to drive a microscopic Carnot engine? The answer is no. At the scale of individual molecules, thermal di usion is far too rapid to permit the maintenance of a temperature gradient. Molecular motors must therefore function isothermally. They must directly transduce chemical energy to mechanical work, without passing through the intermediary of heat.

T. Duke: Modelling Motor Protein Systems

99

1.2 Simple Brownian ratchet

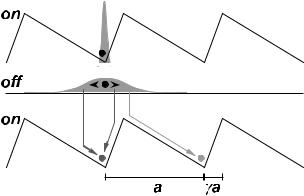
Can microscopic ratchets be employed to rectify Brownian motion at a single, fixed temperature? To demonstrate that they can, it su ces to provide an illustration. Perhaps the simplest Brownian ratchet consists of a particle moving in one dimension in a periodic but asymmetric potential which is switched on and o at regular intervals of time [16–19]. Consider, for example, the saw-tooth potential in Figure 1, characterized by asymmetry factor γ and periodicity a.

Fig. 1. Movement of a Brownian particle in a ratchet potential which is switched on and o at regular intervals of time. The particle, which is localized when the potential is on, starts to di use freely when the potential is turned o and has a Gaussian probability distribution (shown in grey). When the potential is switched back on, the particle slides down the potential gradient. Owing to the asymmetry, there is a higher probability that it hops to the right than to the left.

If the peak of the potential is considerably higher than the thermal energy, the particle tends to be localized at the bottom of one of the wells when the potential is on. But when the potential is switched o , the particle is free to di use by Brownian motion. Suppose that the di usion coe cient is D and that the potential is turned on again after time T . Then if γ2 < DT /a2 < (1 − γ)2, there is quite a high probability that the particle will drop into the next potential well to the right, but only a small chance that it will fall to the left. Thus with continued pulsing of the potential at intervals of time T , the particle moves noisily but, on average, it drifts to the right. The Brownian motion has been rectified. Yet no external force has been applied – the potential is globally flat at all times.

Of course, the laws of thermodynamics have not been violated here; in order to generate directional motion, an external agent has had to do work.

100	Physics of Bio-Molecules and Cells

There is an input of energy each time that the potential is switched on, raising the potential energy of the particle. This energy is subsequently transferred to the environment by viscous dissipation as the particle drifts towards the bottom of the well. Thus the Brownian motion has been rectified at the cost of transforming some mechanical work to heat.

1.3 Polymerization ratchet

We would like to develop a general formalism to study the movement of a Brownian particle in a ratchet potential. An illustrative example which serves as a useful starting point is the process of polymerization of a filament from a large pool of monomers. This is a stochastic process which is driven in the direction of polymer extension by the negative free energy change, ∆G, which occurs each time a monomer is added. If a mechanical force F is applied to the tip of the polymer, however, the growth can be slowed, or even reversed [20, 21]. Because the insertion of a monomer of size a at the tip requires the energy F a, the thermodynamic principle of detailed balance imposes a condition on the rates r± at which monomers bind and unbind at the tip:

r+/r− = e−(F a+∆G)/kT .

(1.1)

The growth velocity v = a(r+ − r−) can be determined if the two rates r+ and r− are known independently. These rates, however, depend on the energy barriers which the system must overcome in order to insert or detach a monomer – barriers which depend on microscopic details of the polymerization process and which are not fixed by thermodynamic laws. Suppose that insertion of a monomer at the end requires passage over a

potential barrier U (F ) which depends on the external force. If U kT , polymerization events are thermally activated with the Arrhenius rate r+ = r0e−U/kT and the growth velocity is

v = r0a e−U (F )/kT	1 − e−(F a+∆G)/kT .	(1.2)

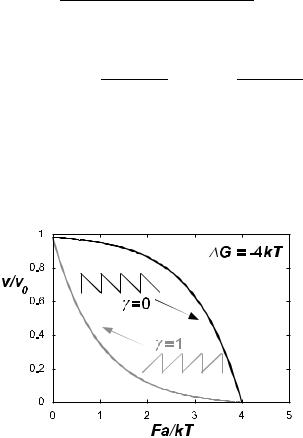
Two important conclusions can be drawn: Thermodynamic laws only determine the stall force for which the velocity vanishes, F0 = −∆G/a; and the form of the force-velocity relationship can vary widely, depending on the unknown function U (F ) which determines the strain-dependence of the polymerization reaction.

Kramers [22] introduced the notion that an individual chemical reaction can be modelled as the stochastic motion of a Brownian particle over a potential barrier. Extending his approach, we see that polymerization in the absence of a force is formally equivalent to stochastic motion in an

T. Duke: Modelling Motor Protein Systems									101

Fig. 2. a) Polymerization of a filament under the constraint of an applied force. b) The stochastic polymerization process may be mapped onto the Brownian motion of a particle in a potential V (x), which is the sum of a periodic potential W (x) and a uniform potential gradient proportional to the polymerization energy ∆G.

e ective energy landscape

V (x) = W (x) −	∆G	x,	(1.3)
	a

where W (x) is a periodic function (which is related to the potential barrier) and x is a position variable along a linear axis (Fig. 2). The polymers of di erent length correspond to the local minima of V (x). A particle moving stochastically in this potential would drift downhill, corresponding to the direction of polymerization. When an opposing force is applied, the total energy of the corresponding particle changes to V (x) + F x. It can be seen that this becomes a periodic function when F = F0 = −∆G/a, at which point there is no net drift of the particle and, correspondingly, polymerization is halted.

The motion of a Brownian particle in a tilted periodic potential, and simulataneously under the influence of an external force F , is most conveniently discussed using the Smoluchowski equation. The probability density P (x, t) of finding the system at position x at time t obeys

∂t P = −∂xJ
J = −	1	[(∂xV + F )P + kT ∂xP ] ,	(1.4)
	ζ

102	Physics of Bio-Molecules and Cells

where J is the current. The stationary solution which satisfies ∂t P stat = 0 corresponds to constant current J and is given by

P stat(x) = e−	kT	A + D 0			x	kT	,	(1.5)
					dye
	V (x)+F x		J			V (y)+F y

where A is a constant of integration and D = kT /ζ is the di usion coe - cient. Normalization (one particle per period) and the condition of periodicity determine both A and the current J . The average velocity v = J a is

v =

a

Da[1 − e−(F a+∆G)/kT ]

,

(1.6)

dx e−

V (x)+F x

x+a

dy e

V (y)+F y

0

kT

x

kT

which is the same as equation (1.2), with an e ective energy barrier

U (F ) = kT ln

e−

−

x

e

−

(1.7)

kT

kT

a

a

0

a dx W

(x)+(F

W (y)+(F

F0 )y

F0)x

x+a dy

and attempt rate r0 = D/a2. If the form W (x) of the energy barrier is known, then the strain-dependence U (F ) can be calculated and the forcevelocity relation determined. For example, if W (x) has minima at x = N a, and sharply peaked maxima at x = (N + γ)a, then U (F ) ≈ U (0) + γaF . Force-velocity relations corresponding to di erent forms of W (x) are shown in Figure 3.

Fig. 3. Growth velocity of a polymer as a function of the restraining force, for two di erent realizations of the periodic potential W (x), whose form is indicated.

T. Duke: Modelling Motor Protein Systems

103

1.4 Isothermal ratchets

The reason for the spontaneous motion of the Brownian particle in the polymerization ratchet is clear; it occurs because of the global tilt of the potential which, in turn, corresponds to the non-equilibrium nature of the polymerization reaction. Yet we have seen, in the preceding example, that directional movement can also occur in a globally flat potential, provided that the potential changes with time. We shall now explore what conditions must be satisfied for such motion to occur. More specifically, we shall focus our attention on a Brownian particle that can exist in a number of di erent states. In each state, the particle experiences a periodic potential Wi(x) = Wi(x + a); and the particle makes stochastic transitions from state i to state j at rate ωij (x). Systems of this type, which generate motion in the absence of an external force, and at a constant temperature, are called

isothermal ratchets [12].

The dynamics of a particle in an isothermal ratchet may be described by generalized Smoluchowski eqations

∂tPi = −∂xJi + j			(ωji Pj − ωij Pi)
Ji = −	1	[(∂xWi + F )Pi + kT ∂xPi]		(1.8)
	ζ

where Pi(x, t) denotes the probability of finding the particle at time t at position x and in state i. The total probability P ≡ i Pi and total current J ≡ i Ji satisfy an ordinary Smoluchowski equation of the type of equation (1.4), but with an e ective potential:

J = −	1	[(∂xVe + F )P + kT ∂xP ] .	(1.9)
	ζ

This can be shown by introducing the local fractions of occupation in conformation i

λi(x) ≡	Pi(x)	,	(1.10)
	P (x)

which describe how P is divided amongst the di erent states. Expressing the total current as

1
J = − i		[(λi∂xWi + kT ∂xλi + λiF )P + kT λi∂xP ]	(1.11)
	ζ
we find		Ve (x) = x dx λi∂xWi.
			(1.12)

i0

104	Physics of Bio-Molecules and Cells

The system generates spontaneous motion (i.e. motion in the absence of the external force F ) if the e ective potential is globally tilted. This tilt can be characterized by the e ective energy di erence per period

a

∆Ge = dx λi∂xWi. (1.13)

i0

In order for ∆Ge to be nonzero, two conditions must be satisfied: (i) the system as a whole, i.e. the potentials Wi(x) and/or the transition rates ωij (x), must be asymmetric with respect to x → −x; (ii) the system must

be out of thermodynamic equilibrium.

If the system is completely symmetric, then so are the functions λi(x) and the integral in equation (1.13) vanishes by symmetry. No spontaneous motion occurs. If the system is in thermodynamic equilibrium, the transition rates satisfy the condition of detailed balance

ωij	= e(Wi −Wj )/kT .	(1.14)
ωji

In this case, the steady state solution is given by the Boltzmann distribution Pistat e−Wi /kT , and the integrand in equation (1.13) is the derivative of the periodic function −kT ln(Σe−Wi /kT ), so ∆Ge = 0. Again, no motion occurs.

To summarize, the two conditions for spontaneous motion in an isothermal ratchet are broken spatial symmetry and broken detailed balance.

1.5 Motor proteins as isothermal ratchets

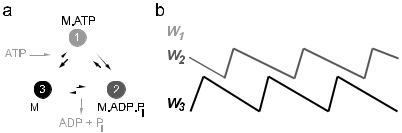
Motor proteins interact with cytoskeletal filaments. Because these are polar polymers, this interaction may be characterized as an asymmetric periodic potential, with the periodicity equal to the monomer size a. Molecular motors also hydrolyse ATP and can therefore exist in a number of distinct chemical states, depending on whether or not nucleotide is bound (and which type of nucleotide is bound). Crucially, the chemical state of the motor modulates the interaction between the motor and the filament. It is therefore natural to model a molecular motor as a particle in an isothermal ratchet. In each state i (identified with the chemical state of the motor) the particle experiences a di erent potential Wi(x) (identified with the motorfilament interaction). A simple illustration is given in Figure 4.

As the hydrolysis reaction proceeds around the cycle, the laws of thermodynamics state that the transition rates satisfy

	ωi→i+1	= e−(Wi −Wi+1 )/kT Θ	i→i+1	(1.15)
	ωi+1→i

T. Duke: Modelling Motor Protein Systems				105

Fig. 4. a) The hydrolysis cycle of a typical molecular motor. The motor passes through a number of distinct chemical states in which a di erent nucleotide (or no nucleotide) is bound. b) The interaction potential between the motor and the cytoskeletal filament depends on the chemical state. In this case the motor in state 1 (with ATP bound) is detached from the filament, and the other two states are bound to the filament.

where

Θi→i+1 = e−∆µi→i+1/kT

(1.16)

and ∆µi→i+1 is the change on chemical potential that would accompany the reaction in free solution.

So we see that the two elements required to generate movement are in place. The polarity of the filaments ensures broken spatial symmetry of the ratchet potentials; and the coupling of the motor-filament interaction to the hydrolysis reaction breaks detailed balance by the factors Θi→i+1, thereby ensuring that the transitions between the ratchet states are not just thermally activated. Note, however, that if the product of the factors around the cycle i Θi→i+1 were equal to unity, global equilibrium would be preserved and no movement would occur. This is not the case in a biological cell because for each traversal of the cycle, one molecule of ATP has been hydrolysed to ADP and Pi. The total free energy change is therefore ∆µATP and i Θi→i+1 = e−∆µATP/kT . The continual manufacture of ATP in the cell maintains the reaction ATP → ADP + Pi out of equilibrium, with ∆µATP ≈ −20 kT . It is the nonequilibrium nature of this reaction which ultimately drives the motor.

1.6 Design principles for e ective motors

We have seen how to generate motion, but what functional form of the potentials and the transition rates would make for an especially e ective motor? Desirable properties of a motor protein such as kinesin, which acts individually to transport substances in the cell, include swiftness of

106

Physics of Bio-Molecules and Cells

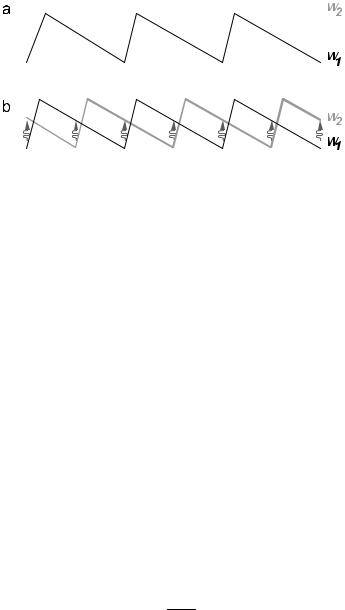
Fig. 5. Examples of two-state isothermal ratchets. In b) the stimulated transitions between the states are localized to the shaded regions.

movement, the ability to resist high loads, and the e cient transduction of chemical energy to mechanical work. Can the formalism that we have developed suggest what principles of design might lead to such properties? We noted that the force-velocity relation can vary widely depending on the shape of the e ective potential, which in turn depends on the detailed functional form of both the periodic ratchet potentials and the transition rates. Nonetheless, we can gain some insight by examining a simple 2-state model.

Consider therefore the system shown in Figure 5a, where the saw-tooth potential W1 (with barrier height W kT ) represents a bound state of the motor, and the flat potential W2 represents a detached state. We assume that the binding rate is constant, ω21 = α, and write the detachment rate as

ω12(x) = αe(W1 −W2 )/kT + Ω

(1.17)

where the first term on the right hand side corresponds to thermal transitions and the rate Ω, which is assumed to dominate, represents transitions that are stimulated by coupling to a non-equilibrium process. The e ective generation of directional movement in this isothermal ratchet requires careful matching of two time scales. First, the particle in the detached state must di use a distance greater than γa, but smaller than a, in the typical time α−1 that it takes to bind. The optimal situation occurs roughly at the midpoint of this range, when

α ≈	kT	·	(1.18)
	γζa2

Second, when in the bound state, the particle must have time to drift to the bottom of the potential well before it detaches again. Taking into account that the force acting on the particle in the bound state is approximately