Physics of biomolecules and cells

T. Duke: Modelling Motor Protein Systems

127

Γ must scale as f R2. Thus the condition M Γ yields the scaling relation

R (κf )1/3 ·

(3.12)

Since the bending modulus of cytoskeletal filaments is known, a simple measurement of the size of the spiral provides a direct measure of the motor protein force.

If the filament is pinned at two separate locations near the leading end, both the position and the vector of the end are fixed. In this case, the solution for short filaments is the serpentine motion that is seen experimentally. However, the asymptotic solution for long filaments is the pattern shown in Figure 20b. While the leading end of the filament writhes from side to side, the back end continually traces out a figure of eight – the curve called the “elastica” [59] which can be obtained by pressing on the ends of a thin elastic rod until both ends meet.

3.6 Undulation of flagella

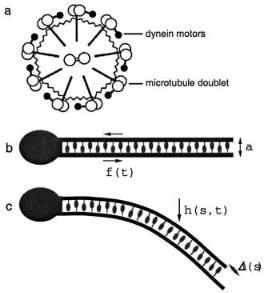
Cilia and spermatzoid flagella share a common structure, called the “axoneme” [60], which is composed of a cylinder of microtubule doublets (Fig. 21a). Dynein motors attached to each doublet interact with the neighbouring doublet around the ring, generating a shear force. Because all of the microtubules are firmly held in place in a basal body (next to the head of a spermatozoan, or at the root of a cilium), the sliding of ajacent microtubule doublets causes to bending of the entire axoneme [61]. Clearly, in order to generate the wavelike undulation of a flagellum, the shear force between a given microtubule doublet must vary with both time and position. Does this require a chemical control mechanism to ensure that the motors on one side of the axoneme work while the motors on the opposite side detach [62]? Or might wave-like motion occur natually as a result of a dynamical instability? The buckling of filaments in a gliding motility assay demonstrates that instabilities can indeed lead to complex periodic movement. In that case, however, the motors exert an external force on the filament. In the axoneme, the motor action is internal. Can a dynamical instability produce undulations in this situation too?

The basic physical properties of the axoneme can be captured by the two-dimensional model shown in Figure 21b, in which a pair of filaments is connected by a set of motor proteins [63]. The rotational symmetry of the axoneme – in which each doublet slides on its neighbour – corresponds to a lack of polarity in the 2-dimensional case. So the motor-mediated interaction between the pair of filaments might be represented as a symmetric isothermal ratchet. As we saw in Section 3.2, this type of system can be bistable, and the total shear force generated between the filaments by the

128	Physics of Bio-Molecules and Cells

Fig. 21. a) Cross-section through an axoneme. b) Model of a flagellum. c) Bending caused when the lower filament slides forwards relative to the upper filament.

team of motors can have either sign. The relative sliding of the filaments in response to this force bends the axoneme, as shown in Figure 21c. Now, this movement is countered by a force derived from the elastic bending of the axoneme. To a first approximation, we can consider the motors to be working against a uniform spring. Then, as discussed in Section 3.4, an oscillatory instability can occur, such the shear force generated by the motors varies periodically.

The simplest model [63] of a flagellum, then, supposes that the force per unit length f generated by the motors is independent of the position s along the axoneme, but varies sinusoidally in time, f = f0 cos ωt. Writing the perpendicular displacement of the axoneme as h(s), the local sliding displacement is ∆(s) = a(∂sh(s) − ∂sh(0)), where a is the distance between the two filaments. This leads to the following equation of motion,

η ∂th = −κ∂s4h − a∂sf,

(3.13)

where κ is the bending modulus and η is the friction coe cient per unit length orthogonal to the axoneme axis (which is approximately equal to the viscosity of the surrounding fluid). To solve for the motion, this equation must be supplemented by two boundary conditions at each end. The

T. Duke: Modelling Motor Protein Systems

129

Fig. 22. Undulation generated by oscillatory motor forces within a flagellum.

solution for the situation correponding to a spermatozoan is shown in Figure 22. A bending wave propagates from the head to the tail, if the head experiences a large viscous drag.

A more general treatment [64] recognizes that the elastic force opposing the action of the motors varies along the axoneme, and that the motor force is therefore also a function of position. Solutions may be obtained by considering the form of the response function relating the local motor force to the local sliding velocity, derived for example from a simple two-state isothermal ratchet model. In this case, the stationary solution is stable when the system is close to equilibrium, but a dynamical instability occurs at a critical value of the control parameter Ω. The dynamical mode that is selected, and the characteristic frequency of the movement, both depend upon the length of the axoneme. Long flagella propogate a bending wave, similar to that shown in Figure 22. Shorter axonemes simply flex from side to side, at a frequency which is governed by equation (3.9), with an e ective spring constant K ≈ κL3 and an e ective friction ζ ≈ η L. The critical frequency is then

ωc ≈	ακ		1/2 1		,	(3.14)
	η			L2

which increases rapidly as the length of the axoneme decreases.

4 Sense and sensitivity: Mechano-sensation in hearing

4.1 System performance

The performance of our senses is remarkable, and none more so than hearing. The faintest sounds that we can hear impart no more energy, per cycle, than the thermal motion. At the same time, the ear can cope with loud noises that carry more than twelve orders of magnitude more energy. And, of course, it can analyze frequency: two tones that di er by a few percent can be resolved. Just how this astonishing feat is achieved has been a puzzle for over a century, but recent research is beginning to penetrate the mystery.

130	Physics of Bio-Molecules and Cells

The key to the ear’s acuity is an active system of sound detection [65]. The ear is powered. That this was likely to be the case was first realized by Gold [66], more than fifty years ago. He pointed to a problem with the theory of hearing propounded by Helmholtz [67], who had argued that the ear uses a set of inertial resonators to capture the energy of sound waves. Given that the cochlea is filled with fluid, and the likely size of the resonators is a few microns at most, the strong damping precludes a sharp resonant response. Gold proposed that the ear must work like a regenerative radio receiver, and add in energy at the very frequency it is trying to detect. It was clear to him that such a mechanism must be very delicate, however, as it would require a positive feedback of exactly the right magnitude to cancel the damping. Any less and the ear would be insensitive; any more and it would ring spontaneously.

It was not until the 1970s that the idea of an active cochlea began to be taken seriously. At that time, the first successful measurements on a living ear revealed it to respond far more sensitively than the dead cochlea [68, 69]. Subsequently it was discovered that the ear can spontaneously emit sounds [70]. A microphone placed in the ear cannal usually records a faint hum, but occasionally shrill whistles can be detected as well. Clearly, something within the cochlea is oscillating. In this section, we shall explore how active oscillators can help the ear to hear, and discuss whether motor proteins might be an important component of the active system.

4.2 Mechano-sensors: Hair bundles

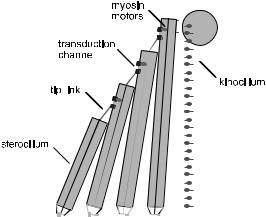
A hair bundle is an appendage measuring a few microns high that sticks up above the surface of every hair cell [71] (see Fig. 23). It consists of a number of stereocilia (each composed of a bundle of actin filaments) which slope up against each other to form a pyramidal structure. Each stereocilium is connected to its neighbour by a fine filament, called a “tip link”. Shear flow in the cochlea fluid causes the whole bundle to deflect, with each stereocilium pivoting at its base, so that the tip links get stretched. Each tip link connects directly to a tension-gated transduction channel in the cell membrane, which admits potassium ions. So the deflection leads to a change in the ionic current that, it turn alters the cell potential. The hair bundle is therefore a transducer which provides a very direct conversion of a mechanical stimulus to an electrical signal.

In the 1980s it was discovered that hair bundles can oscillate spontaneously [72]. This behaviour had been very di cult to reproduce, however, until recently when it bacame possible to control of the extracellular ionic concentrations, so that they resemble the conditions in vivo [73]. In this situation, oscillations occur quite readily. It appears that calcium ions, which are present at low concentration in the fluid surrounding the bundle,

T. Duke: Modelling Motor Protein Systems

131

Fig. 23. Hair bundle of a non-mammalian vertebrate.

and which are also admitted by the transduction channel, are crucial to the active process.

Hair bundles also contain molecular motors. Attached to the transduction channel are a number of myosin-1C motors. They are believed to play a role in adapting the hair bundle to varying cellular conditions, by maintaining the proper tension in the tip links [74]. But they might also be more directly involved in generating bundle oscillations. The hair bundles of nonmammalian vertebrates also incorporate a “kinocilium”, which has the same architecture as an axoneme. The dynein motors within this structure might also play an active part in the hair bundle response.

4.3 Active amplification

There is considerable evidence, then, that hair bundles contain a forcegenerating dynamical system that can generate spontaneous oscillations at a characteristic frequency ωC. In general, the behaviour of such a nonlinear dynamical system may be described by a control parameter C. Above a critical value, C > Cc, the system is stable; for C < Cc it oscillates spontaneously. At the critical point C = Cc, which is a Hopf bifurcation, the system has remarkable response properties. Because the behaviour close to critical points is generic, we can calculate these properties without a detailed knowledge of the physical process that gives rise to the dynamical instability [75–77].

132 Physics of Bio-Molecules and Cells

If a stimulus force f (t) is applied at frequency ω, the hair bundle dis-

placement x(t) has a principal component at that same˜frequency. So writ-
ing the complex Fourier coe cients at frequency ω as f			and x˜, the reponse
may be expressed as a systematic expansion
˜	2	x˜ + ...,	(4.1)
f = A x˜ + B |x˜|

where A(ω, C) and B(ω, C) are two complex functions. For a system that undergoes a Hopf bifurcation, the first nonlinear term is cubic. The bifurcation point is characterized by the fact that A vanishes for the critical frequency, A(ωc, Cc) = 0.

Suppose that the system is poised right at the critical point, C = Cc. Then the response to a stimulus at the critical frequency, ω = ωC has amplitude

		˜ 1/3
	|x˜| ≈	|f |	1/3	·	(4.2)
		|B|

This is a highly compressive response, which boosts weak signals much more than strong signals. Indeed, the gain

	r =	|x˜|		1	(4.3)
		˜		˜ 2/3
		|f |		|f |

becomes arbitrarily large for small forces. The critical Hopf oscillator acts as a nonlinear amplifier.

If the stimulus frequency di ers from the critical frequency, the linear term in equation (4.1) is non-zero and can be expressed to first order as A(ω, Cc) A1 (ω − ωc). When this term exceeds the cubic term in equation (4.1), active amplification is lost and the response becomes linear

		˜
	x˜	|f |	·	(4.4)
		|(ω − ωc)A|
	| |

The bandwidth of active amplication ∆ therefore depends on the level of the stimulus:

	∆		|B|1/3	f˜ 2/3.	(4.5)
		≈	|A1| |
				|

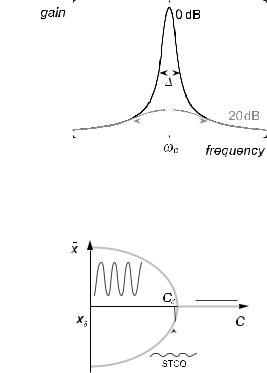
The resonant response of a critical Hopf oscillator is summarized in Figure 24. The active system acts as a sharply tuned high-gain amplifier for weak stimuli, and as a low-gain filter for strong stimuli. These main features are displayed by the response of the basilar membrane in the mammalian cochlea [78].

T. Duke: Modelling Motor Protein Systems							133

Fig. 24. Hopf resonance. The gain and the sharpness of response are much greater for a weak stimulus (black), than for a stimulus of ten times greater amplitude (grey).

Fig. 25. The working point of the self-tuned system is just on the oscillating side of the bifurcation, yielding self-tuned critical oscillations (STCO).

4.4 Self-tuned criticality

The Hopf resonance is perfectly suited to the ear’s needs. It permits frequency descrimination; it boosts faint sounds; and the strongly compressive response provides a huge dynamic range – the twelve orders of magnitude of sound energy that we can comfortably hear give rise to hair bundle displacements that vary by only a factor of one hundred. To profit from the nonlinear amplification, however, each oscillator has to be very close to its critical point. Clearly some kind of regulation mechanism is required to ensure that this is the case.

A feedback mechanism that links the reponse of the system to the control parameter can permit the system to operate automatically close to the bifurcation point, whatever its characteristic frequency [76] (Fig. 25). Suppose that some mechanism causes the control parameter to decrease as long as the system does not oscillate. After some time, critical conditions will be

134	Physics of Bio-Molecules and Cells

reached and spontaneous oscillations will ensue. The onset of oscillations triggers an increase of the control parameter which tends to restore stability. Hence the system converges to an operating point close to the bifurcation point. The following simple feedback, which changes C in response to deflections x, illustrates the general idea:

1	∂t C =	1		x2	− 1	(4.6)
C		τ		δ2

where δ is a small amplitude. If no external force is applied, this feedback, after a relaxation time τ , tunes the control parameter to a value Cδ (just less than Cc) for which spontaneous oscillations with |x˜| δ occur. These small-amplitude oscillations are referred to as self-tuned critical oscillations. Maintained on the threshold of vibrations by this control mechanism, a hair bundle is exquisitely sensitive to purturbation by periodic stimuli at its characteristic frequency.

4.5 Motor-driven oscillations

What is the physical basis of the dynamical system that generates the oscillations? Because motor proteins are specialized to produce motility, they are an obvious candidate. One possibility is that the kinocilium is the motile element of non-mammalian hair bundles [76]. We have already seen that an axoneme can flex at a frequency that depends on its length, equation (3.9). So in this case, the characteristic frequency of a hair bundle would depend on its architecture. Tall bundles would oscillate at lower frequencies than short bundles. This agrees with what is known about the tonotopic organization of hair cells in the cochlea [79]. It is also plausible that it is the myosin-1C motors joined to the transduction channels, rather than the dynein motors in the kinocilium that cause the oscillations. In either case, the characteristic frequency of the bundle can be significantly faster than the cycle rate of individual motors.

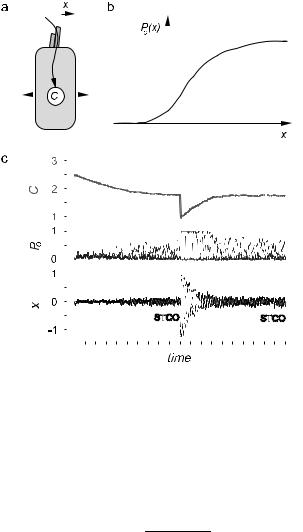
How could self-tuning to the critical point be realized in this system? One possibility is that the influx of calcium ions through the transduction channel down-regulates the motor activity (Fig. 26a) [76]. In this case, the Ca2+ concentration plays the role of the control parameter C. Assuming that ion pumps in the cell membrane constantly pump Ca2+ out of the cell, C obeys the dynamical equation

∂tC = −	C	+ J Po(x),	(4.7)
	τion

where τion is the ionic relaxation time and J is the Ca2+ current through an open transduction channel. The probability Po(x) that a channel is open

T. Duke: Modelling Motor Protein Systems

135

Fig. 26. Self-tuning mechanism. a) Calcium flux through the hair cell. b) Channel open probability P (x). c) The bundle settles down to self-tuned critical oscillations after a relaxation time τion, whether the Ca2+ concentration C is intially

too high or too low.

depends on the hair bundle displacement, as shown in Figure 26b. the typical sigmoidal relation, of the form

1

Po(x) = 1 + Ae−x/δ

This is

(4.8)

that is expected if the channel makes rapid stochastic transitions between an open and a closed state, gated by the tension in the tip link. The coe cient A is large, so that when the bundle is still, there is only a slight probability that the channel is open. However, owing to the curvature of Po(x) at x = 0, the mean probability of the channel being open increases if the bundle becomes unstable and starts to oscillate. Equation (4.7) then implies that C rises. If the Ca2+ ions down-regulate the motors, for example by decreasing the rate Ω at which they detach, the system moves back towards

136	Physics of Bio-Molecules and Cells

the quiescent regime. This feedback control is a robust way of generating self-tuned critical oscillations, as illustrated in Figure 26c.

4.6 Channel compliance and relaxation oscillations

An alternative mechanism by which oscillations might be generated is suggested by recent micromanipulation experiments on hair bundles [80]. When the tip of a bundle is abruptly displaced by a small amount, the bundle reacts by generating the force in the opposite direction. Indeed, the instantaneous force-displacement relation of the bundle (i.e. the relation obtained before adaptation processes mediated by motors or calcium have an a ect) displays a region of negative slope (Fig. 27a).

Fig. 27. a) Two-state transduction channel with a lever arm. b) The forcedisplacement relation has a region of instability owing to the channel compliance. c) The action of the myosin-1C motors can push the system around the arrowed curve, generating relaxation oscillations.