Physics of biomolecules and cells

T. Duke: Modelling Motor Protein Systems			107
W/a, this condition may be written
Ω <	W	·	(1.19)
	ζa2

Thus this very simple isothermal ratchet generates spontaneous motion only if the chemical transition rates are adjusted to match the dynamical parameters of the system. Moreover, it cannot support a significant load, despite the high value of the force that is generated in the bound state. This happens because the particle in the detached state slips backwards very readily. Indeed, the motor will stall if it slips a distance of order γa when it is detached, as it will then fail to di use beyond the peak of the potential W1. Taking into account that the slip velocity is F/ζ and the time spent detached is α−1, with α specified by equation (1.18), the stall force is

F0 ≈	kT	·	(1.20)
	a

The force that the motor can support is determined by the thermal energy and not by the chemical energy available to pump the transitions between states. In summary, this simple 2-state ratchet would be a very poor design for a motor: it is quite awkward to get it to operate at all; and when it does work, it is puny and wasteful of energy.

A system which provides a vastly improved performance [12,23] is shown in Figure 5b. In this case, the potential W2 has a similar saw-tooth form to W1, but is shifted by half the lattice constant. In addition, both transitions are assumed to be stimulated at a position-dependent rate Ω(x), which is significant only when the particle is close to the bottom of a well. The advantages of this system are clear. The particle in state 1 moves down the long slope of the potential W1 to the bottom of the well, whereupon it makes a stimulated transition to state 2. It then moves down the slope of W2, reverting to state 1 when it reaches the bottom. There is now no need to match the kinetic rates with the dynamical parameters to generate e ective movement. And because the particle always experiences a potential gradient, the stall force is now determined by the barrier height, F0 ≈ W/a, rather than the thermal energy. From equation (1.16), it can be seen that in order to stimulate the transitions from the bottom of the wells, the magnitude of the chemical energy change ∆µij that accompanies each change of state must exceed the potential energy change, which is equal to half the barrier height. If |∆µ12| = |∆µ21| ≈ W/2, little energy is dissipated as heat during the transitions and the maximal mechanical e ciency of the system can be close to unity. In this case, the stall force is governed by the chemical potential ∆µATP = ∆µ12 + ∆µ21 that is available to power the motor,

F0 ≈ −	∆µATP	·	(1.21)
	a

108	Physics of Bio-Molecules and Cells

The principles of e ective energy transduction outlined above appear to be used by actual molecular motors. It is believed, for example, that kinesin moves along microtubules by advancing its two motor domains in a coordinated, “hand-over-hand” fashion [24, 25]. Such cooperation would require a switch-like mechanism, whereby the binding of one domain induces a chemical change in the other, stimulating it to detach. This model corresponds quite closely to the type of isothermal ratchet we have just discussed, where the potential W1 represents the kinesin-microtubule interaction with one of the motor domains bound, and W2 the interaction with the other domain bound. Suppose that the domains can only bind at localized binding sites, situated at the minima of the potentials, and that binding causes the stimulated detachment of the other head. Then the transitions between the two potentials are localized, as in Figure 5. The ratchet generates directional movement very e ectively and can support a high load. Another molecular motor that makes use of localized transitions to ensure a high e ciency of operation is the F1 component of ATP synthase. In this case, three motor domains work together in a highly coordinated way to generate rotational motion [26]. At any one time, each domain is at a di erent stage of the hydrolysis cycle: one has ATP bound, one has ADP bound and the third has no nucleotide bound. This motor can be modeled as a three-state ratchet [27] in which the potentials have o set minima, and transitions between states are controlled by a molecular switch so that they take place only at particular angles of rotation.

More generally, position-dependence of the transition rates can be associated with strain-dependence of the chemical reactions, and a shift in the position of the potential minima between two states can be associated with a conformational change of the motor domain. In the next section we shall explore these concepts in the context of the interaction between myosin and actin.

2 Pulling together: Mechano-chemical model of actomyosin

2.1 Swinging lever-arm model

Isothermal ratchets are a convenient formalism for discussing the generic behaviour of motor proteins. However, for specific motor systems, for which structural and chemical information is available, models based on chemical kinetics can be more appropriate since they may more immediately be related to experimental data. Such is the case for actomyosin. The resulting models [28–34] are termed crossbridge models, reflecting the fact that the myosin head forms a transient bridge between the thick and thin filaments in a muscle fibre.

T. Duke: Modelling Motor Protein Systems

109

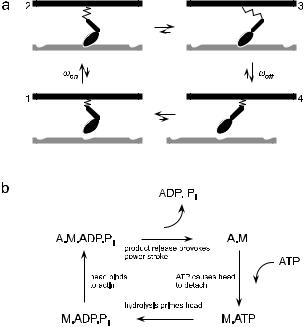
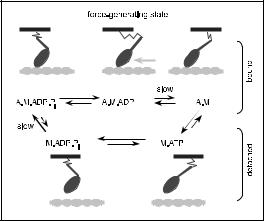
Early electron micrographs of crossbridges bound to the thin filament indicated that there were two, structurally distinct, attached states [35]. Recent crystallographic studies [36], together with micromanipulation experiments [37,38], have refined this view, strongly suggesting that the distal portion of the myosin head acts as a lever arm to amplify small changes in structure occurring at the nucleotide binding site. This has led to the swinging lever-arm model [39], which is shown in Figure 6a.

Fig. 6. Swinging-lever arm model of the mechano-chemical cycle of actomyosin.

The basic assumption is that the myosin head can undergo a structural change, provoked by chemical reactions at the nucleotide binding site, which alters the orientation of the lever arm. Biochemical techniques [40] have elucidated the nucleotide reactions which are coupled to the structural change and which modulate the myosin-actin interaction (Fig. 6b). The hydrolysis cycle proceeds in four steps: (1) ATP hydrolysis occurs when the myosin is detached. Energy is not liberated at this stage but is used instead to prime the lever arm. (2) The head binds to the thin filament. (3) The products of hydrolysis, Pi and ADP are released, provoking a significant rotation of the lever arm. The large change in free energy which accompanies product release is not liberated as heat, but is stored in an elastic element

110	Physics of Bio-Molecules and Cells

which connects the myosin head to the thick filament. Because the head is now in a state that generates a shear force between the thick and the thin filament, this transition between bound states is often referred to as the power-stroke. If the force is not compensated by an applied load, the filaments will slide relative to one another. (4) Finally, a new molecule of ATP binds to the myosin head, destabilising its interaction with the actin filament. The myosin detaches, completing the cycle.

In the cell, the concentration of ATP is maintained well above its equilibrium value, so that the actomyosin cycle proceeds only in the forward direction (the free energy of hydrolysis is approximately 20kBT , so the probability of cycling backwards is e−20 ≈ 10−9 in the absence of an external load). As successive hydrolysis reactions occur, the mysoin acts as an “oar” which “rows” along the thin filament.

2.2 Mechano-chemical coupling

Kinetic models of myosin action may be based on this 4-state cycle, but care must be taken to ensure consistency with the laws of thermodynamics. Each state i can be considered to be internally at equilibrium, and may therefore be characterised by a Gibbs free energy Gi which includes contributions from the myosin-actin interaction and the nucleotide-myosin interaction. In contrast to ratchet models, the motor domain is taken to be immobilized when it is bound to the actin binding site. Nevertheless, the crossbridge is assumed to be compliant, so that the thin filament can still move relative to the thick filament. Then the free energy of the actomyosin complex Gi depends on the relative displacement x of the thin and the thick filaments, owing to the mechanical deformation of the myosin molecule. In a given state, the actomyosin undergoes Brownian motion in the potential Gi(x) and the instantaneous force exerted on the thin filament by the myosin head is equal to the gradient of the potential, Fi = ∂xGi.

For each transition between a pair of states, the principle of detailed balance dictates that the ratio of forward and reverse rates is related to the di erence of the free energies:

ωij	= e−(Gj −Gi )/kT .	(2.1)
ωji

In transitions involving a bound state, Gj −Gi will, in general, depend on the relative displacement of the thick and thin filaments, so either the forward or the reverse transition rate (or both) must be strain-dependent. Put another way, the kinetic rates depend on the force experienced by the myosin molecule. This mechano-chemical coupling [30] is the key to understanding motor protein action. Thermodynamics provides strong constraints on theoretical models. The relations between kinetic rates must be associated

T. Duke: Modelling Motor Protein Systems

111

'P

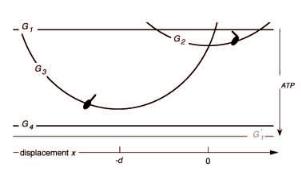
Fig. 7. Free energies of actomyosin states in the swinging lever-arm model.

with the mechanical properties of the molecules. However, there remains considerable freedom to choose the functional form of individual rates.

In most mechano-chemical models of actomyosin, the dependence of free energy on position is simplified and given a physical interpretation by supposing that the myosin molecule contains a linear elastic element. Thus two parameters characterise the mechanical properties of a crossbridge: the distance d that the distal end of the lever moves when the myosin makes a transition between the two attached states; and the spring constant K. The force exerted by the myosin head in each state is then Kx and K(x + d), respectively, where x is the shear displacement between the two filaments. The values of the structural parameters are di cult to measure experimentally, but recent data suggests that d ≈ 5 nm and K ≈ 1 pN/nm [41].

The corresponding free energies Gi are indicated in Figure 7. Note that traversal of the cycle in the clockwise direction is tightly coupled to the hydrolysis of one molecule of ATP so, although the actomyosin returns to the same state, the free energy of the whole system has changed by ∆µATP.

2.3 Equivalent isothermal ratchet

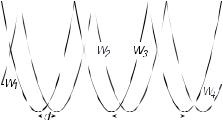
Although crossbridge and isothermal ratchet models are not entirely equivalent, it is possible to construct a ratchet model which strongly resembles a crossbridge description. As an example, we outline an isothermal ratchet which would generate approximately the same dynamics as the swinging lever arm model. The ratchet model involves transitions between four different potentials Wi, which represent the actomyosin interaction, as shown in Figure 8. Potentials W1 and W4 represent detached states and are therefore flat. The potentials W2 and W3, which represent the two bound states,

112		Physics of Bio-Molecules and Cells

Fig. 8. 4-state ratchet equivalent to the swinging lever-arm model.

are each symmetric and periodic, with period l equal to the distance between the binding sites on the thin filament (l = 34 nm for actin). The minima of W2 are shifted by d relative to those of W3, and the curvature of both potentials is ∂x2W = K. Transitions between these states are stimulated by chemical reactions occurring at the nucleotide binding site. Indeed, the assumption of tight-coupling in the swinging lever-arm model implies that the transition rates are governed by equations (1.15) and (1.16). Although the individual periodic potentials Wi of this ratchet are symmetric, the system as a whole is asymmetric if d < l/2, thereby satisfying one of the conditions for movement. The second condition is that the transitions between the potentials Wi violate detailed balance, i.e. that the product of the factors Θij

is not equal to unity. Since ΠΘij = exp(−∆µATP/kT ), this is assured if the nucleotide hydrolysis reaction is maintained out of equilibrium.

This 4-state model di ers from the swinging lever-arm model in only one respect: the ratchet potentials Wi corresponding to the bound states are periodic and have multiple minima, whereas the free energies Gi of the bound states in the crossbridge picture are assumed to have a single minimum (whose location varies according to which site on the thin filament the myosin head is bound). Whether this di erence is significant is a question of time scale. If transitions between states occur more rapidly than di usion over the potential barrier, then the two models di er only in insubstantial detail.

2.4 Many motors working together

Many millions of myosin molecules work together to drive muscle contraction. A hundred or so myosin molecules interact with each thin filament, a few thousand filaments make up each sarcomere, and a single myofibril fibre is typically composed of thousands of sarcomeres in series. A single muscle fibre is then formed by a bundle of a few thousand myofibrils. In order to

T. Duke: Modelling Motor Protein Systems											113

Fig. 9. Protein friction.

understand muscle contraction, therefore, we need to construct a statistical mechanical model, based on the mechano-chemical cycle of an individual myosin molecule that has been outlined above. How do many motors act together to drive a single thin filament? Clearly they can combine their e orts to generate a large force. But they can also get in each other’s way and hinder sliding. We shall explore this potential problem first, and see how proteins can create friction [42].

Consider a set of N proteins, each of which independently binds to a filament at rate ωon and detaches at rate ωo , as shown in Figure 9. For the moment, we will assume that these proteins are not motors (and so do not undergo a conformational change when bound) but that, like myosin, they form crossbridges of elasticity K. Suppose that an external force F is applied to the filament, causing it to move with steady velocity v. The mean fraction of proteins that is bound at any one time is r = ωon/(ωon + ωo ), and the probability that each of these proteins has strain x is p(x) = (v/ωo ) exp(−xωo /v). When a protein detaches, the elastic energy 12 Kx2 is dissipated as heat. The total dissipation rate due to the proteins is therefore N rωo 12 K<x2> = ζproteinv2, where

	ζprotein =	N rK	(2.2)
		ωo

is the e ective friction coe cient associated with the proteins. Unless the number of bound proteins is very small, or the detachment rate is very rapid, this protein friction is considerably larger than the viscous drag exerted on the filament by the surrounding fluid.

Now suppose that the N proteins are myosin molecules, each of which is executing its mechano-chemical cycle. Let us make a simple assumption about the kinetics, and suppose that the rate-limiting steps are the binding to (2→3) and detachment (4→1) from the filament, and that these occur at strain-independent rates ωon and ωo . The fraction r of motors bound to the filament is then fixed. It is convenient to characterize the properties of an individual motor by a unitary velocity vunit = ωond and a unitary force Funit = Kd. When the filament is loaded with an external force F , its

114	Physics of Bio-Molecules and Cells

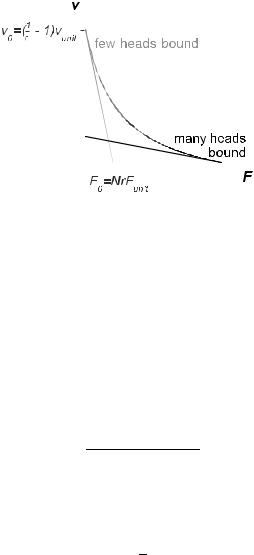
Fig. 10. For strain-independent transition rates, the force-velocity relation is linear. Rapid sliding and a high stall load can be combined if the fraction of bound motors increases with the load (curve).

equation of motion is Fmot = F +ζv, where Fmot is the total force generated by the motors. It is clear that when v = 0, each bound motor generates force Funit, so that the stall force is

F0 = N rFunit.

(2.3)

Since the system is linear, the force-velocity relation must be a straight line

with slope equal to the total e ective friction ζprotein + ζ. Thus, the velocity at zero load is

v0 =	vunit	(2.4)
	r/(1 − r) + τviscωon

where τvisc = ζ/N rK is the viscous relaxation time of the system. If the viscous relaxation is rapid compared to chemical reaction times, as is the

case in a sarcomere,

1	− 1 .
v0 ≈ vunit r		(2.5)

Then, as indicated in Figure 10, a small fraction of bound motors (r 1) produces rapid sliding in unloaded conditions, but provides only a low stall force. If, on the other hand, the majority of motors are bound (r ≈ 1), the sliding is slow, but the stall force is high. Neither situation is ideal for muscle contraction, where a combination of rapidity and strength is required. However, this combination can be achieved by regulating the

T. Duke: Modelling Motor Protein Systems

115

fraction of bound motors r according to the load. What is required is some kind of control mechanism whereby few motors are bound at zero load, but more are recruited as the load increases.

2.5 Designed to work

How can regulation of the fraction of bound motors be accomplished? The observation that the two products of hydrolysis are not released simultaneously provides a clue. Phosphate is released first, and this provokes the power-stroke of the lever arm. Subsequently ADP is released more slowly, and this makes way for the immediate binding of a new ATP molecule, which precipitates detachment of the head from the actin filament. Thus the detachment step (4 → 1) is really controlled by the rate of ADP release. Now, we might expect that the departure of any ligand from the nucleotide binding site would result in a small change of conformation there, which gets amplified by the lever arm. Thus ADP release might cause the distal end of the lever arm to shift by a modest amount δ, as indicated in the more complete model of the actomyosin cycle [33] shown in Figure 11. Mechanochemistry would then make the rate of ADP release strain-dependent. If a muscle fibre is loaded isometrically so that the filaments are prevented from sliding, each bound motor will be strained, exerting approximately

the unitary force Funit = Kd. As a result, the small movement of the lever arm accompanying ADP release will involve an amount of mechanical work

equal to Funitδ. This slows down the reaction by a factor exp(−Kdδ/kBT ), compared to the unstrained situation at zero load. The delayed detachment

Fig. 11. Model of the actomyosin cycle.

116	Physics of Bio-Molecules and Cells

augments the fraction of motors bound to the thin filament, helping to support the high load.

It thus appears that the lever-arm structure of myosin serves a dual function. The large swing of the arm on phosphate release is designed to generate force. And the smaller shift on ADP release is designed to endow muscle with a “continuous automatic transmission”, by adjusting the number of motors appropriately to the load. This second shift need not very big (δ ≈ 1 nm), which may explain why it has not been observed for skeletal-muscle myosin. Movement of the lever on ADP release has, however, been detected in a number of other myosins [43, 44].

There is a second aspect of the structural design of myosin, which concerns the strength of its elastic element. Clearly this should not be too weak, or a motor would produce only a feeble unitary force Funit. However, it should not be too strong either, since the power-stroke would be inhibited if the mechanical work required to move the lever arm, 12 Kd2, exceeded the free energy change that accompanies phosphate release, ∆µPi . In fact, it appears that the molecular design of myosin pushes this limit as far as possible, choosing a value of 12 Kd2 that slightly exceeds ∆µPi . This is slightly surprising, because it means that an individual myosin molecule would be ine ective, not having enough energy to power its stroke. But a team of motors working together is actually more e cient in this case, for the following reason: when a myosin head binds to the filament, it cannot immediately execute its power-stroke, but the transition is postponed until filament sliding (due to the action of other motors) has strained the motor and reduced the work accompanying the power-stroke to ∆µPi . Consequently, all of the energy of phosphate release gets stored in the elastic element, and none gets wasted as heat.

2.6 Force-velocity relation

Although muscle contraction is clearly a dynamical process, individual pairs of thick and thin filaments may be treated as though they are in “quasimechanical equilibrium”. This is because the viscous relaxation time is short compared to the time scale of chemical reactions, so that each time an individual motor changes state, the filaments quickly readjust their position as shown in Figure 12.

A simple stochastic simulation algorithm can therefore be used to determine the sliding velocity for a given load [33]. The resulting force-velocity relation is shown in Figure 13. The shape of the curve is concave [45], owing to the regulation of the fraction of bound motors discussed above. However, another interesting feature is apparent. As the load approaches the stall force (or “isometric tension”), the velocity drops abruptly to zero. Precisely this type of behaviour is seen in the experimentally determined