Physics of biomolecules and cells

T. Duke: Modelling Motor Protein Systems

137

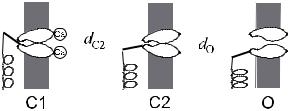
One potential explanation of this behaviour is channel compliance [80, 81]. Suppose that the transduction channel has a lever arm, similar to that of a myosin molecule, which amplifies the small movements associated with the opening and closing of the channel (Fig. 27b). Then when the hair bundle is pushed a distance x the positive direction, adjacent stereocilia are sheared by y = γx, where γ is a geometric factor that depends on the bundle height. The increased tension Ttl in the tiplinks causes the channels to open. Indeed, assuming that the channel kinetics is rapid enough for there to be an equilibrium between open and closed states, the open probability Po is

Po =	1	,	(4.9)
	1 + Ae−Ktlyd/kT

where Ktl is the elastic constant of the tip link, d is the swing of the lever arm and A is a dimensionless constant whose value depends on the free energy di erence of the two channel states. The associated movement of the lever arm diminishes the tension in the tip links, so that

Ttl = Ktl(y − dPo).

(4.10)

The total reactive force of the bundle has contributions from both the tip links and the deformation of the stereocilia pivots,

F = N (γTtl + Kspx),

(4.11)

where N is the total number of stereocilia and Ksp is the e ective Young modulus due to a single sterocilium. The force-displacement relation resulting from equations (4.9–4.11) has a region of negative slope if

Ktld2 > 4kT .

(4.12)

In this situation, there is a range of applied forces for which the bundle is bistable. If the position of the adaptation motors is fixed, the hair bundle will settle at one or other of the stable positions. However, this state of a airs can be upset if calcium down-regulates the motors, as suggested above. Suppose, for example, that the bundle is at the fixed point with the higher value of x, for which there is a high probability that the transduction channels are open. The Ca2+ ions entering through the channel bind to the motors, causing a fraction of them to detach; the diminishing force exerted by the motors causes the tension in the tip links to fall, and the bundle to move backwards. As indicated in Figure 27a, the fixed point vanishes at a critical value of the motor force, and the system then abruptly jumps to the other fixed point. At this lower value of x, the channels are mostly closed. The resulting drop in calcium concentration augments the number of bound motors, increasing the tension in the tip links until the lower fixed

138		Physics of Bio-Molecules and Cells

Fig. 28. Three-state channel, in which one of the closed states is stabilized by calcium.

point becomes unstable, whereupon the hair bundle jumps back to its initial position.

This dynamics, whereby the myosin-1C motors shift the bundle from one stable fixed point to another, results in relaxation oscillations with a characteristic form, shown in Figure 27c. Oscillations of this type have been observed in an in vitro system [73, 80]. It is not clear, however, whether this mechanism forms the basis of the active amplier. There is no obvious way that the system could be regulated to the critical point at which the oscillations have vanishing amplitude.

4.7 Channel-driven oscillations

There is a second adpatation process that modifies the transduction current, which is much faster than the mechanism mediated by the myosin-1C motors [74, 82]. It depends on the concentration of calcium ions outside the cell and is believed to be caused by Ca2+ ions binding to the transduction channels and favouring their closure. Thus, a more appropriate model of the channel might incorporate three states, as shown in Figure 28, in which one of the closed states is stabilized by the binding of Ca2+. The dynamics of calcium, which enters through the transduction channels and is continually pumped out of the cell, as described by equation (4.7), provides a fast feedback. By shifting the channel states and modifying the contribution of the channel compliance, it modifies the force-displacement relation. If the feedback is strong enough, the region of negative sti ness is eliminated and the system has a single fixed point [83]. However, this fixed point may be either stable or unstable and, in the latter case, the bundle executes limit cycle oscillations. Thus the interaction of the calcium with the channel is able to generate a Hopf bifurcation. With their long lever arms, the channels e ectively act like molecular motors, driven by calcium rather than by ATP.

T. Duke: Modelling Motor Protein Systems

139

The characteristic frequency of oscillation depends on two time scales

	ωc ≈	1		1/2
				,	(4.13)
		τmechτion

where τion is the relaxation time of the calcium concentration and τmech is the viscous relaxation time of the bundle. It scales as

ωc	L3τion			1/2	(4.14)
				,
		N

and thus depends strongly on the architecture of the bundle.

Crucially, the stability of the fixed point is determined by the location of the myosin-1C motors. If these motors generate a large force, the hair bundle oscillates; if they generate a small force, the bundle is quiescent. This suggests that the function of the myosin-1C motors is to tune the system to the critical point [83]. Down-regulation of the motors by Ca2+ entering through the channels when the bundle oscillates could fulfil this function.

Thus, the two adaptation mechanisms that have been identified for hair cells can together generate self-tuned critical oscillations. Calcium acting on the channels creates a dynamical instability and the molecular motors, acting on a slower time scale, adjust the system to the immediate vicinity of the critical point.

4.8 Hearing at the noise limit

Hair bundles are subject to noise from a number of sources. In addition to the Brownian forces of the molecules in the surrounding fluid, the stochastic nature of the force-generating system adds further randomness to the system. How can the bundle detect a weak signal in the presence of this noise?

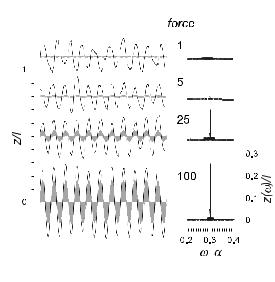
As a consequence of the stochasticity, the self-tuned critical oscillations are irregular, as illustrated in Figure 26c. The response of a self-tuned hair bundle to a sinusoidal force with a frequency approximately equal to the bundle’s characteristic frequency [76] is illustrated in Figure 29. For weak stimuli, the amplitude of the oscillation does not increase with the amplitude of the applied force; this is because the small response to the stimulus is masked by the noisy, spontaneous motion. Instead, the phase of the hair-bundle oscillation becomes more regular; as it does so, a peak emerges from the Fourier spectrum at the driving frequency. The height of the peak grows as the cube root of the stimulus amplitude, following the generic behaviour at a Hopf bifurcation specified by equation (4.2).

This suggests how a hair bundle can achieve its remarkable sensitivity to weak stimuli [76]. By profiting from the periodicity of a sinusoidal input,

140

Physics of Bio-Molecules and Cells

Fig. 29. Detection in the presence of noise. Response to sinusoidal forces of di erent magnitude (left), and Fourier transform of the response (right). The response of an equivalent passive system in the absence of noise is indicated in grey.

and measuring phase-locking rather than the amplitude of response, the mechano-sensor can detect forces considerably weaker than those exerted by a single molecular motor (if the bundle were a simple, passive structure, its response to such forces would be smaller than its Brownian motion). An important implication of this detection mechanism is that the signal must be encoded by the interval between spikes elicited in the auditory nerve. Paradoxically, the stochastic noise serves a useful purpose. It ensures that the self-tuned critical oscillations of the hair bundle are incoherent, so that the pattern of spontaneous firing in the nerve is irregular. Against this background, the regular response to a periodic stimulus can easily be detected. Another beneficial feature of noise arises from the fact that weak stimuli do not increase the amplitude of oscillation above the spontaneous amplitude. Thus the Ca2+ concentration remains constant, the hair bundle stays in the critical regime, and active amplification can be sustained indefinitely.

The active system of detection, in which motor proteins play a key role, explains how the ear can detect sound waves whose energy per cycle is similar to that of the thermal noise.

My understanding of motor protein systems has benefited from conversations with numerous colleagues, including S. Block, L. Bourdieu, S. Camalet, J. Howard, A.J. Hudspeth, A.F. Huxley, S. Leibler, M. Magnasco, P. Martin, and A. Vilfan. I am especially indepted

T. Duke: Modelling Motor Protein Systems

141

to F. J¨ulicher and J. Prost, on whose research much of this course is based. The Royal Society provided funding. Last but not least, I thank the organisers and participants of the School who made the summer at Les Houches such an enjoyable experience.

References

[1]T. Kreis and R. Vale, Cytoskeletal Motor Proteins (Oxford University Press, New York, 1993).

[2]B. Alberts, D. Bray, J. Lewis, M. Ra , K. Roberts and J.D. Watson, Molecular Biology of the Cell (Garland, New York, 1994).

[3]D. Bray, Cell Movements (Garland, New York, 2001).

[4]J. Howard, Mechanics of Motor Proteins and the Cytoskeleton (Sinauer, Sunderland Massachusetts, 2001).

[5]M.O. Magnasco, Phys. Rev. Lett. 71 (1993) 1477.

[6]J. Prost, J.F. Chauwin, L. Peliti and A. Ajdari, Phys. Rev. Lett. 72 (1994) 2652.

[7]R.D. Astumian and M. Bier, Phys. Rev. Lett. 72 (1994) 1766.

[8]M.O. Magnasco, Phys. Rev. Lett. 72 (1994) 2656.

[9]C.S. Peskin and G.F. Oster, Biophys. J. 68 (1995) 202.

[10]T.A.J. Duke and S. Leibler, Biophys. J. 71 (1996) 1235.

[11]I. Der`enyi and T. Vicsek, Proc. Natl. Acad. Sci. USA 93 (1996) 6775.

[12]F. J¨ulicher, A. Ajdari and J. Prost, Rev. Mod. Phys. 69 (1997) 1269.

[13]R.D. Astumian, Science 276 (1997) 917.

[14]M.E. Fisher and A.B. Kolomeisky, Proc. Natl. Acad. Sci. USA 96 (1999) 6597.

[15]R.P. Feynman, R.B. Leighton and M. Sands, The Feynman lectures on physics, vol. I, chap. 46 (Addison-Wesley, Reading MA, 1966).

[16]A. Ajdari and J. Prost, C.R. Acad. Sci. Paris II 315 (1992) 1635.

[17]J. Rousselet, L. Salome, A. Ajdari and J. Prost, Nature 370 (1994) 446.

[18]L.P. Faucheux, L.S. Bourdieu, P.D. Kaplan and A.J. Libchaber, Phys. Rev. Lett. 74 (1995) 1504.

[19]J.S. Bader, R.W. Hammond, S.A. Henck, M.W. Deem, G.A. McDermott, J.M. Bustillo, J.W. Simpson, G.T. Mulhern and J.M. Rothberg, Proc. Natl. Acad. Sci. USA 96 (2000) 13165.

[20]C.S. Peskin, G.M. Odell and G.F. Oster, Biophys. J. 65 (1993) 316.

[21]M. Dogterom and B. Yurke, Science 278 (1997) 856.

[22]H.A. Kramers, Physica 7 (1940) 284.

[23]A. Parmeggiani, F. J¨ulicher, A. Ajdari and J. Prost, Phys. Rev. E 60 (1999) 2127.

[24]W.O. Hancock and J. Howard, Proc. Natl. Acad. Sci. USA 96 (1999) 13147.

[25]K. Visscher, M.J. Schnitzer and S.M. Block, Nature 400 (1999) 184.

[26]P.D. Boyer, Annu. Rev. Biochem. 66 (1997) 717.

[27]H. Wang and G. Oster, Nature 396 (1998) 279.

[28]H.E. Huxley, Science 164 (1969) 1356.

[29]A.F. Huxley and R.M. Simmons, Nature 233 (1971) 533.

[30]T.L. Hill, Prog. Biophys. Mol. Biol. 28 (1974) 267.

[31]E. Eisenberg, T. Hill and Y. Chen, Biophys. J. 29 (1980) 195.

[32]S. Leibler and D.A. Huse, J. Cell Biol. 121 (1993) 1357.

[33]T.A.J. Duke, Proc. Natl. Acad. Sci. USA 96 (1999) 2770.

142	Physics of Bio-Molecules and Cells

[34]A. Vilfan, E. Frey and F. Schwabl, Euro. Phys. Lett. 45 (1999) 283.

[35]M.K. Reedy, K.C. Holmes and R.T. Tregear, Nature 328 (1987) 536.

[36]I. Rayment, H.M. Holden, M. Whittaker, C.B. Yohn, M. Lorenz, K.C. Holmes and R.A. Milligan, Science 261 (1993) 58.

[37]J.T. Finer, R.M. Simmons and J.A. Spudich, Nature 368 (1994) 113.

[38]J.E. Molloy, J.E. Burns, J. Kendrick-Jones, R.T. Tregear and D.C.S. White, Nature 378 (1995) 209.

[39]K.C. Holmes, Curr. Biol. 7 (1997) R112-R118.

[40]R.W. Lymn and E.W. Taylor, Biochem. 10 (1971) 4617.

[41]C. Veigel, M.L. Bartoo, D.C. White, J.C. Sparrow and J.E. Molloy, Biophys. J. 75 (1998) 1424.

[42]K. Tawada and K. Sekimoto, J. Theor. Biol. 150 (1991) 193.

[43]M. Whittaker, E.M. Wilson-Kubalek, J.E. Smith, L. Faust, R.A. Milligan and H.L. Sweeney, Nature 378 (1995) 748.

[44]C. Veigel, L.M. Coluccio, J.D. Jontes, J.C. Sparrow, R.A. Milligan and J.E. Molloy, Nature 398 (1999) 530.

[45]A.V. Hill, Proc. R. Soc. B 126 (1938) 136.

[46]K.A.P. Edman, J. Physiol. 404 (1988) 301.

[47]R.J. Podolsky, Nature 188 (1960) 666.

[48]K.A.P. Edman and N.A. Curtin, J. Physiol. 534 (2001) 553.

[49]F. J¨ulicher and J. Prost, Phys. Rev. Lett. 75 (1995) 2618.

[50]M. Badoual, F. J¨ulicher and J. Prost, Proc. Natl. Acad. Sci. USA 99 (2002) 6696.

[51]S.A. Endow and H. Higuchi, Nature 406 (2000) 913.

[52]D. Riveline, A. Ott, F. J¨ulicher, O. Cardoso, S. Magnusdottir, J.L. Viovy and J. Prost, Eur. Biophys. J. 27 (1998) 403.

[53]F. J¨ulicher and J. Prost, Phys. Rev. Lett. 78 (1997) 4510.

[54]F. J¨ulicher, C.R. Acad. Sci. Paris Serie IV 2 (2001) 849.

[55]J.W.S. Pringle, in R.T. Tregear, Insect Flight Muscles (North-Holland, Amsterdam 1977).

[56]K. Yasuda, Y. Shindo and S. Ishiwata, Biophys. J. 70 (1996) 1823.

[57]H. Fujita and S. Ishiwata, Biophys. J. 75 (1998) 1439.

[58]L. Bourdieu, T.A.J. Duke, M.B. Elowitz, D.A. Winkelmann, S. Leibler and A. Libchaber Phys. Rev. Lett. 75 (1995) 176.

[59] A.E.H. Love, A	Treatise on the Mathematical Theory of Elasticity (Dover,
New York, 1944).

[60]I.R. Gibbons, J. Cell Biol. 91 (1981) 107s.

[61]C.J. Brokaw, Science 178 (1972) 455.

[62]M. Murase, The Dynamics of Cell Motility (Wiley, New York, 1992).

[63]S. Camalet, F. J¨ulicher and J. Prost, Phys. Rev. Lett. 82 (1999) 1590.

[64]S. Camalet and F. J¨ulicher, New J. Phys. 2 (2000) 1.

[65]P.J. Dallos, J. Neurosci. 12 (1992) 4575.

[66]T. Gold, Proc. R. Soc. B 135 (1948) 462.

[67]H.L.F. Helmholtz, On the Sensations of Tone (Dover, New York, 1954).

[68]W.S. Rhode, J. Acoust. Soc. Am. 49 (1971) 1218.

[69]P.M. Sellick, R. Patuzzi and B.M. Johnstone, J. Acoust. Soc. Am. 72 (1982) 131.

[70]D.T. Kemp, J. Arch. Otorhinolaryngol. 224 (1979) 37.

T. Duke: Modelling Motor Protein Systems

143

[71]A.J. Hudspeth and V.S. Markin, Physics Today 2 (1994) 22.

[72]A.C. Crawford and R. Fettiplace, J. Physiol. 364 (1985) 359.

[73]P. Martin and A.J. Hudpeth, Proc. Natl. Acad. Sci. USA 96 (1999) 14306.

[74]J.R. Holt and D.P. Corey, Proc. Natl. Acad. Sci. USA 97 (2000) 11730.

[75]Y. Choe, M.O. Magnasco and A.J. Hudspeth, Proc. Natl. Acad. Sci. USA 95 (1998) 15321.

[76]S. Camalet, T.A.J. Duke, F. J¨ulicher and J. Prost, Proc. Natl. Acad. Sci. USA 97 (2000) 3138.

[77]V.M. Eguiluz, M. Ospeck, Y. Choe, A.J. Hudspeth and M.O. Magnasco, Phys. Rev. Lett. 84 (2000) 5232.

[78]L. Robles and M.A. Ruggero, Physiol. Rev. 81 (2001) 1305.

[79]L.G. Tilney and J.C. Saunders, J. Cell Biol. 96 (1983) 807.

[80]P. Martin, A.D. Mehta and A.J. Hudpeth, Proc. Natl. Acad. Sci. USA 97 (2000) 12026.

[81]J. Howard and A.J. Hudpeth, Neuron 1 (1988) 189.

[82]D.P. Corey and A.J. Hudspeth, J. Neurosci. 3 (1893) 962.

[83]A. Vilfan and T. Duke (to be published).

COURSE 4

DYNAMIC FORCE SPECTROSCOPY

E. EVANS AND P. WILLIAMS

Physics and Pathology, University of

British Columbia, Vancouver, Canada

V6T 2A6; Biomedical Engineering,

Boston University, Boston, MA

02215, USA

Pharmaceutical Sciences, University of Nottingham, Nottingham, UK

Contents
Part 1: E. Evans and P. Williams		147
1 Dynamic force spectroscopy. I. Single bonds		147
1.1	Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	147
	1.1.1 Intrinsic dependence of bond strength on time frame
	for breakage . . . . . . . . . . . . . . . . . . . . . . . . . . .	148
	1.1.2 Biomolecular complexity and role for dynamic force
	spectroscopy . . . . . . . . . . . . . . . . . . . . . . . . . .	148
	1.1.3 Biochemical and mechanical perspectives of bond strength . 150
	1.1.4 Relevant scales for length, force, energy, and time . . . . . .	153
1.2	Brownian kinetics in condensed liquids: Old-time physics . . . . .	154
	1.2.1 Two-state transitions in a liquid . . . . . . . . . . . . . . .	155
	1.2.2 Kinetics of first-order reactions in solution . . . . . . . . . .	156
1.3 Link between force – time – and bond chemistry . . . . . . . . . .		158
	1.3.1 Dissociation of a simple bond under force . . . . . . . . . .	158
	1.3.2 Dissociation of a complex bond under force: Stationary rate
	approximation . . . . . . . . . . . . . . . . . . . . . . . . .	159
	1.3.3 Evolution of states in complex bonds . . . . . . . . . . . . .	163

1.4Testing bond strength and the method of dynamic force spectroscopy164

1.4.1 Probe mechanics and bond loading dynamics . . . . . . . . 165 1.4.2 Stochastic process of bond failure under rising force . . . . 168 1.4.3 Distributions of bond lifetime and rupture force . . . . . . . 169

1.4.4Crossover from near equilibrium to far from equilibrium

unbonding . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172

1.4.5E ect of soft-polymer linkages on dynamic strengths of bonds175

1.4.6Failure of a complex bond and unexpected transitions

		in strength . . . . . . . . . . . . . . . . . . . . . . . . . . .	177
1.5	Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		185
Part 2: P. Williams and E. Evans			186
2 Dynamic force spectroscopy. II. Multiple bonds			187
2.1	Hidden mechanics in detachment of multiple bonds . . . . . . . . .		187
2.2	Impact of cooperativity . . . . . . . . . . . . . . . . . . . . . . . .		188
2.3	Uncorrelated failure of bonds loaded in series . . . . . . . . . . . .		191
	2.3.1 Markov sequence of random failures . . . . . . . . . . . . .		191
	2.3.2	Multiple-complex bonds . . . . . . . . . . . . . . . . . . . .	193
	2.3.3	Multiple-ideal bonds . . . . . . . . . . . . . . . . . . . . . .	194
	2.3.4	Equivalent single-bond approximation . . . . . . . . . . . .	195
2.4	Uncorrelated failure of bonds loaded in parallel . . . . . . . . . . .		198
	2.4.1 Markov sequence of random failures . . . . . . . . . . . . .		198
	2.4.2	Equivalent single-bond approximation . . . . . . . . . . . .	198
2.5	Poisson statistics and bond formation . . . . . . . . . . . . . . . .		199
2.6	Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .		203

DYNAMIC FORCE SPECTROSCOPY

E. Evans1 and P. Williams2

Part 1: E. Evans and P. Williams

1 Dynamic force spectroscopy. I. Single bonds

1.1 Introduction

Weak-noncovalent interactions govern structural cohesion and mediate most of life’s functions from the outer membrane surface to the interior nucleus of a cell. On laboratory time scales, the energy landscape of a weak bond is fully explored by Brownian-thermal excitations, and energy barriers along its dissociation pathway(s) become encoded in a rate of unbonding that can range from 1/µs to 1/year. When pulled apart with a ramps of force, the dissociation kinetics become transformed into a dynamic spectrum of unbonding force as a function of the steepness of the force ramps (loading rates). Expressed on a logarithmic scale in loading rate, the spectrum of breakage forces begins first with a crossover from near equilibrium to far from equilibrium unbonding and then rises through ascending regimes of strength. These regimes expose the prominent energy barriers traversed along the dissociation pathway. Labelled as dynamic force spectroscopy [7, 10], this approach is being used to probe the inner world of biomolecular interactions [7, 8, 13, 14, 23, 24, 26, 30] and reveals energy barriers that are di cult or impossible to access by solution assays of nearequilibrium kinetics. These hidden barriers are crucial for specialized dynamic functions of molecules.

In this first chapter of our tutorial, we begin with an outline of the physics needed to understand the impact of force on lifetime of a single bond. Then deriving prescriptions for rate of transition under force, we analyze the stochastic process of unbonding in a probe experiment and

1Physics and Pathology, University of British Columbia, Vancouver, Canada V6T 2A6; Biomedical Engineering, Boston University, Boston, MA 02215, USA.

2Pharmaceutical Sciences, University of Nottingham, Nottingham, UK.

c EDP Sciences, Springer-Verlag 2002