Дегтяренко Введение в физику неупорядоченных конденсированных 2011

=

=

=

=

=

=

=

=

=

=

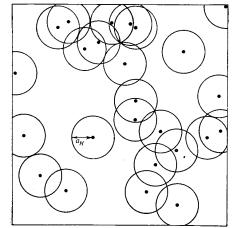
РисK=PKNTK=Примесные центры в полупроводнике=

=

Если нет заметной химической тенденции к сегрегации приJ месей или к образованию кластеров при кристаллизации образцаI= то примеси будут случайно распределяться по узлам решеткиI=как в= любом сильно разбавленном сплавеK= Для электронов проводимоJ стиI=однакоI=роль=«размера»=примесного атома играет эффективный= боровский радиус= аeI= отвечающий низшему примесному уровнюK= Этот= = радиус может в= NM =или= NMM =раз превышать постоянную реJ

шетки исходного кристаллаK=Соответственно концентрацию примеJ сей в= NMJ4= –= NMJO= атK =B =следует считать очень= «большой»I =так как=

здесь оказывается несправедливым предположение о независимоJ сти электронных процессовI=протекающих на отдельных примесяхK=

=

=

=

=

=

=

=

9N=

=

РАЗДЕЛ=4= МОДЕЛИ И МЕТРИКА КОНТИНУАЛЬНОГО=

БЕСПОРЯДКА=

=

4.N.=Континуальные модели=

=

Атомная структура конденсированной среды часто приводит= к осложнениям в математической теории неупорядоченных системK= Такие важные физические характеристики системыI= как электронJ ная плотность и масса ядраI= сконцентрированы в очень малых обJ ластяхK=Поэтому их трудно описать при помощи линейных комбиJ наций гладкихI= делокализованных функцийK= В ряде случаев на= практике выясняетсяI= что= «глубокие»= внутренние свойства атомов= не так уж важныK= Эффекты упорядоченияI= беспорядка замещения= или топологического беспорядка возникают скорее благодаря маJ лым вариациям плотности заряда во всем объеме материалаI=нежеJ ли за счет больших и сильно локализованных ее изменений в преJ делах атомных остововK=

Таким образомI=при построении феноменологических теорий= часто бывает удобно воспользоваться континуальным представлеJ ниемI=игнорируя атомную структуру веществаK==

РазумеетсяI= именно так следует поступатьI= рассматривая исJ тинно макроскопические процессыI= например распространение= звука в океане или прохождение света звезд через атмосферу и раJ диоволн в ионосфереK= Материал рассматривается при этом как неJ прерывная средаI=состав которой определяет локальную плотностьI= упругостьI= коэффициент отраженияI= диэлектрическую проницаеJ мость и тK =дKI =тK =еK =параметрыI =фигурирующие в волновом уравнеJ нииK=Такой подход оправданI=так как здесь имеют место==возмущеJ

нияI=длина волны которых значительно превышает типичное расJ стояние между атомамиK==

Сдругой стороныI=в приложении к тепловым колебаниям или=

кдвижению электронов в неупорядоченной конденсированной= среде континуальная трактовка редко бывает оправданаK= Тем не=

менееI= математическое сходство этих задач с соответствующими=

9O=

=

задачами макроскопической физики наводит на мысль о томI= что= небесполезными могут оказаться и моделиI=в которых флуктуации= плотности или вариации локального кристаллического порядка= рассматриваются просто как физические причины изменений Jло кального потенциалаI=плотностиI=скорости фононов и тK=дK=

Тем не менееI=иногда удается в простой форме отразить влиJ яние довольно сложных структурных характеристик беспорядкаK= РассмотримI= напримерI= эффективную потенциальную энергию= электрона в жидком металлеK= Эта функция характеризует многоJ электронную системуI=иI=строго говоряI=соответствующий потенциJ ал нельзя представить в виде простой суперпозиции атомных Jпо тенциалов:= он может зависеть от многоатомных характеристик= структуры жидкостиI= например от средней локальной концентраJ ции атомовK=

Аналогичные соображения можно использовать и для опреJ деления эффективной потенциальной энергии носителей заряда= вблизи края зоны в аморфном полупроводнике или для вычисления= локальных упругих постоянных в стеклеK=

Вкратце остановимся на статистических характеристиках= случайной функции= xEoF в пространстве=o одноI=двух или трех изJ

мерений и покажемI= чем обусловлены некоторые		геометрические=
ее свойстваK= Пусть= o есть вектор координат на		плоскостиK= Тогда=
функция= xEoF определяет высоту случайной поверхностиK=
=	4.O.=Однородные случайные поля==
	=
Случайное поле= xEoF можно определитьI= только задавая его=
статистические	характеристикиK= Введем различные функции расJ
пределения для	величин= xEoF K= ТакI= функция= m (xI o) определяет=

плотность вероятности найти случайную величину= x в интервале= x ® x + dx точке= oK= В силу предполагаемой однородности расJ

сматриваемого поля эта функция не должна зависеть от=oK== Предположим для простотыI= что любая постоянная компоJ

нента поляI= например среднее значение потенциалаI= исключена из=

9P=

=

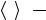
рассмотренияI= тK= еK= среднее значение= x равно нулюK= Это среднее=

значение можно представить:=

NF в виде интеграла по большомуI=но конечному объему=sI=в= котором определен вектор=oX=

OF в виде интеграла по статистическому ансамблю очень= большого числа одинаковых объемовX=в таком ансамбле величина= x в любой точке пространства принимает все возможные свои знаJ

ченияK==

Утверждение о равенстве двух указанных интегралов осноJ вывается на существовании эргодической гипотезы:=

x = N	r r	E4KNF=
	× òxEoF × do = òx× mExF × dx K=
s

На первый взглядI= функцией= m (x) может быть любая полоJ

жительная функцияI=удовлетворяющая условию нормировки=EинтеJ грал от нее по всему объему должен быть равен единицеFK==

Однако этого еще недостаточно для адекватной характериJ стики случайного поляK= Говоря математическим языкомI= статистиJ ческие характеристики случайного поля можно полностью опредеJ

r

литьI= только задавая функционалm (xI o)I= представляющий собой=

предельный случай=s-точечной функции распределения при= s ® ¥ K== Надо ввести двухточечныеI= трехточечные и K=т дK= функции= распределения:=в общем случае=sJточечная функция распределения=

r r r

ms (xNI oNX xO I oO XKxs I os ) определяет вероятность тогоI=что= x приJ

нимает значение= xN в точке= oN I= xO =J=в точке= oO и тK=дK=Только в неJ физическом случае патологически разрывного поля можно предпоJ ложитьI= что величины= x в= «соседних»=точках распределены незаJ

висимоK==

Функции распределения должны удовлетворять ряду соотJ ношений:==

94=

=

-интегрируя величину= ms по любой пространственной переJ менной=EнапримерI= oN F=или усредняя ее по всему ансамблю полеJ вой переменной= xN I==должны получить функцию= ms-N X==

-значения случайного поля= xN и= xO в двух точках= oN и= oO =

при= o = oN - oO ® ¥ должны быть статистически независимыX=

-если поле не только однородноI=но и изотропноI=то двухтоJ

чечная функция распределения заметно упрощается:=она непреJ

rr

менно должна иметь вид:= mO ExNI oNXxO I oO F º mO ExNIxOX oF X=

- неявно принятое предположение о кусочной непрерывности=

функции= x(o) приводит к томуI=что величины= xN и= xO		стремятся к=
одному и тому же значениюI=когда= oN стремится к= oO K=
Таким образомI=имеем:=
ur	ìdExN - xO F × mExF====при===o ® MI
mO ExNI xOX oF ® í		====E4KOF=
	îmExO F × mExNF====при===o ® ¥K

С учетом этих ограничений функция= mO I= описывая распредеJ ление двух величин= xN и= xO I=зависит от трех переменных и ее трудJ но выразить в простом видеK =Здесь опять теория беспорядка замеJ щения в решетке указывает нам подходящий способ описания Jос новных характеристик функции= mO K= Введем автокорреляционную= функцию поля следующим образом:=

	ur	= òòxNG ×xO × mO ExNIxOX oFdxN × dxO K====E4KPF=
GEoF =	xGEMF ×xEoF
	xO	ò	x O	× m ExF × dx
				N

В выражениях такого типа удобно рассматривать=x как комJ плексную переменнуюI= вещественность которой в дальнейшем= легко будет обеспечить с помощью тривиальных дополнительных=

условийK=Как видноI=функция= G(o) будет монотонно уменьшаться= при увеличении=oI=изменяясь в следующих пределах:=

9R=

=

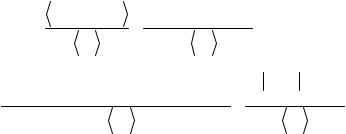
		ìN====при===o ® MI	===============================E4K4F=
	GEoF ® í
		îM===при===o ® ¥K
Здесь ясно видна аналогия с параметром порядка и с полной=
корреляционной функциейK= Длина= i будет			определять типичный=
пространственный	размер	любой= топологической черты поля =
x(o) I=будь то=«пик»=или=«долина»K=
Однородность	поля=	x(o) можно	интерпретировать как=

трансляционную инвариантность в статистическом смыслеK= Для= описания такого поля естественно воспользоваться плоскими волJ

rur

нами= eiqo I= для которых волновые векторы=q выбираются такI=чтоJ бы удовлетворить соответствующим граничным условиям в больJ шом объеме= sK= Для любого компонента данного= ансамбля случайJ ных полей=Eлюбой реализацииF=можно ввести представление Фурье:=

ur	rur
xEoF = åXEqF ×eiq o K=
r
q
Комплексная амплитуда= XEqF	явно определяется		обратным=
	ur	rur	ur

интегральным преобразованием:===== XEqF =s -NòxEoF ×e-iqod o K=

Вычислим теперь автокорреляционную функциюK= Пользуясь= эргодической гипотезойI= можем выполнить следующие стандартJ ные преобразования:=

	r	r r r
GEoF =	xG (M )× x(o )	= òxG × x(o + o¢ do¢)	=
	xO	s xO

G

r

r

r r

r r r

)r

r

O

r

r

ò å X

i×(-qo¢+q¢(o +o¢ )

×e

i×q×o

(q )×X

q(¢

×e)

do¢

å X (q

¢ )

r r

¢

r

q Iq

=

q

xO

s

xO

=E4KRF=

K

Этот результат совершенно аналогичен ранее полученному и= справедлив для любого члена ансамбляK= Определим спектральную= плотность поля=Eили спектр мощностиF=равенством:=

9S=

=

r	r O		E4KSF=
b (q )=	X(q¢ )	K=

Основную роль для дальнейшего играет теорема Винера = – =

Хинчина:= для любого случайного поля спектральная плотность= есть фуръе-образ автокорреляционной функцииK=

Зная общие свойства функции= G(o)I= можем сделать опредеJ

ленные выводы и о соответствующих свойствах= b (q) K= Последняя=

функция должна быть положительно определеннойX= для изотропJ ного поля она может зависеть только от волнового числа=qI=а не от=

направления	в обратном пространствеK= Исходя из условий= E4KSF= и=
пользуясь	стандартными приемами	исследования интегралов=

ФурьеI= можно показатьI= что= b (q) стремится к нулюI =когда число=

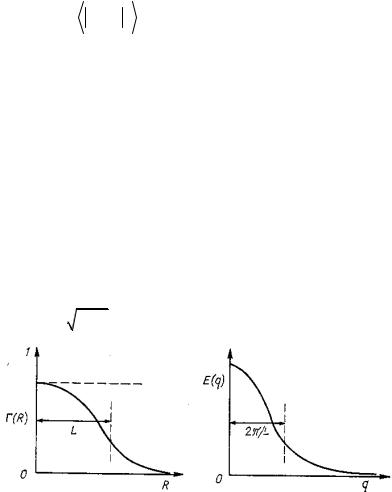
q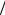Op становится больше обратной длины корреляции= i-N =EрисK4KNF= ОчевидноI= спектральная плотность составляет необходимый элеJ мент описания любого случайного поляK= В какой мере она достаJ точна для этой цели?=Перепишем равенство=E4KSF=в виде:=

r

X(q )=

=

=

=

=

=

=

=

=

=

=

r	ij(q)	K=	E4KTF=
b q	( ×e)

а=======================================================б=

РисK=4KNK=Автокорреляционная функция=EаFI=спектральная= плотность=EбF=

=

Видно теперьI=что это равенство определяет амплитуду кажJ дой= EкомплекснойF= фурье-компонента поляK= Если бы были известJ

9T=

=

ны еще и все фазы = j(q) I =то= = поле= x(o) определялось бы одноJ

значноK= Можно думатьI= что случайный характер поля проявляется= как раз в статистических свойствах фаз различных компонент= ФурьеI=фигурирующих в формуле=E4KTFK=

=

4.P.=Гауссовы случайные поля==

=

Простейшее предположениеI=которое можно сделать относиJ тельно фазовых переменных= f(q) I= состоит в их статистической=

независимости для различных величин= qI= изменяющихся в интерJ вале= -p до= p K= Это предположение точно совпадает с концепцией= спектрального беспорядка в решеткеI= использованной ранее для= описания спиновых волн и фононовK=Однако там речь шла о динаJ мических модахI= можно было предположитьI= что взаимодействие= между ними невеликоK= В данном случае непрерывное случайное= поле представляет собой=статическую характеристику беспорядкаI= «замерзшего»=в системе в процессе ее образованияX= представление= о спектральном беспорядке здесь уже не обязательноK= Более тогоI= заметимI=что фазовый угол= f(q) в действительности может выстуJ

пать в роли измеряемой на опыте локальной характеристики поляK= ДействительноI=эта величина зависит от объема образца и от некоJ торых незаданных граничных условийI=определяющих квантование= q в данном объемеK= Искусственность упомянутого требования осоJ бенно подчеркивается тем обстоятельствомI= что фазовая переменJ ная= f(-q) должна быть равна= f(q) для каждого значения= qI=коль=

скоро требуемI=чтобы функция= x(o) была вещественнойK=

Преимущество этого метода реализуются в построении каноJ нической формы случайного поляI= статистические свойства котоJ рого определены для всех порядков функций распределенияK=

ДействительноI=распределение= x само по себе очень простоеK= Из выражений==

98=

=

r	r r	r
	iqo
x(o) = åX(q )×e		I==== X(q )=
r
q

r	ij(q)	===
b q	( ×e)

в=EпроизвольнойF= точке= o=Z=M=получаем для вещественной величиJ

ны= x :=

x =	å		ë	û	E4K8F=
	q	O ×cos éf(q )ù ×X(q )I=
где фазы= f(q)			распределены случайно в интервале от= -p		до= p K=

Поскольку число членов этой суммы стремится к бесконечностиI= выражение=E4K8F=удовлетворяет условиям применимости=центральJ

ной предельной теоремы теории вероятностиK=

Указанное здесь условие необходимоI= но еще недостаточно= для тогоI= чтобы была справедлива центральная предельная теореJ маK=Нужно ещеI=чтобы дисперсия каждого слагаемого была ограниJ ченнойI= а сумма этих дисперсий неограниченно возрастала при= стремлении числа членов суммы к бесконечностиK=

В теории вероятностей показываетсяI =что в этом случае пеJ ременная= x подчиняется стандартному нормальному или гауссову=

	распределению:=	N		(		)
	m (x )=		×exp		-xO L Op O		I=	E4K9F=
		p × Op
	N
	где= p O есть дисперсия случайного поляI=тK=еK p O º xO							= åb (q )K=
								q
	Таким образомI= рассматриваемое						случайное	поле определяJ

ется величиной= p и видом автокорреляционной функции= G(o)I= в=

данном случае не приходится обращаться к спектральному предJ ставлениюK=

Многоточечные распределения и более высокие моменты= случайного поля также можно явно вычислить с помощью станJ дартных методов теории вероятностейK==

ТакI=напримерI=двухточечное распределение должно бытьI=по= сути делаI= не чем инымI= как совместным распределением Гаусса=

для переменных с корреляционной функцией= G(o)I=тK=eK=

99=

=

			N		æ		x O + x	O	O - Ox x	GEoF	ö
					ç		N		N O		÷
	mO ExNXxO X oF =			×exp	ç	-					÷ KE4KNMF=
		(Op )p O éN- GO EoFùN O					(Op )pO éN- GO EoFù
					ç						÷
	ë		û		è				ë	û	ø

Из выражения=E4KNMF=видноI=что функция= mO удовлетворяет условию=

ur	ìdExN - xO F × mExF====при===o ® M	K=
mO ExNI xOX oF ® í
	îmExO F × mExNF====при===o ® ¥

Поскольку многие физические свойства системI= обусловленJ ные случайными полямиI= зависят от этой функцииI= то формула= E4KNMF=оказывается очень полезнойK=

Однако условие спектрального беспорядка для гауссовой= статистики очень=искусственноK=Возникает вопросI=при каких друJ гих общих условиях будут справедливы соотношения=E4K9F=и=E4KNMFK= В соответствии с центральной предельной теоремой это возJ

можно в случаеI=когда функцию= x(o) удается представить в виде=

суммы большого числа независимых случайных переменных=EприJ мер смK=на рисK4KOFK=

В качестве примера применения этого правила к стационарJ ной случайной функции времени можно привести теорему КэмпJ беллаK=Дробовой шум тока в электрической цепи можно записать в= виде суммы функций отклика= c (t ):=

¥

f EtF = å c Et - t à F I===========================E4KNNF=

à =-¥

где времена прихода электронов=tà случайны и независимыK=ТеореJ ма Кэмпбелла гласитI= что распределение= fEtF= переходит в гауссово=

распределениеI= если		скорость		прихода электронов неограниченно=
возрастаетK==
АналогичноI= в		трехмерном случае поле должно быть предJ
ставлено в	виде суперпозиции= «потенциалов»I= центрированных					в=
случайных	точках=	o à	с	объемной	плотностью= kI= тK=	еK=
r	r r

xEoF = åvEo - o à F K=

à

NMM=

=