Дегтяренко Введение в физику неупорядоченных конденсированных 2011

yl+NEMF = yl Exl FX

N

¶yl +N

N

¶yl

K=

ESKOMF=

×

-

×

= dl

¶x

¶x

yl +N

x=M yl

x=xl

Подставляя выражение= ESKN9F= в условия= ESKOMFI= получаем лиJ нейные уравнения для последовательных амплитуд возбуждения== Eul Iul¢FX Eul+NIul¢+NF K==

В матричной форме эти уравнения имеют вид:=

é

cosEcx

FX

N

×sinEcx

F

ù

æu

ö

ê

l

c

ú

æu

ö

+N

l

ç l

÷

= ê

ú

×ç l

÷ K==ESKONF=

èul¢+N ø

ê-csinEcx F + d

cosEcx

FX

cosEcx

F +

dl

×sinEcx

F

ú

èul¢ø

l

l

l

ú

ê

l

l

c

ë

û

Если отвлечься от физического смысла возбуждения= r à I= то=

полученное выражение имеет такую же формуI=что и соотношение= ESKNSFK=Для упорядоченной системы все матрицы переноса= T были= быI=как и в формуле= ESKN8FI=одинаковы для всех узловK=Для наших= неупорядоченных моделей элементы матриц= T надо определять= статистическиI= задавая функцию распределения случайных переJ менных=x и/или=dK=

RK=Рассмотренная модель есть достаточно частный случайK=ЛюJ бую одномерную потенциальную энергию=s (x) можно представить в=

виде одномерной последовательности=«атомных потенциалов»= vl (x) I=

разделенных участками=Eможет бытьI=бесконечно узкимиFI=на которых= потенциальная энергия равна нулю= EрисK= SKNFK= Таким образомI= матеJ матическая задача сводится к исследованию возбужденийI= распроJ странение которых вдоль цепочки описывается уравнениями типа= ESKNSFX= при этом элементы матрицы= T à суть случайные переменJ

ныеK= Метод матрицы переноса=ESKNSF= можно использовать для люJ бых теоретических моделей возбуждений в одномерной цепочкеK= СлучайI= когда возбуждение= r имеет только две компонентыI =обJ ладает достаточной общностьюK= Он описывает большинство модеJ лей колебательных или электронных возбуждений в цепочке=

NON=

=

«сплава»=или=«жидкости»=EрисKSKOFK=Эти физические задачи матемаJ тически сводятся к изучению результатов преобразования двухJ мерного вектора= r при последовательном умножении его на матJ рицы= T à =J=матрицы=O=×=O=со случайными элементамиK==

=

=

=

=

=

=

=

=

=

=

=

=

=

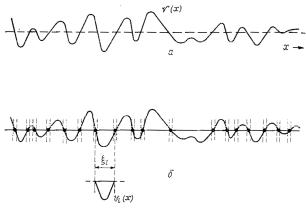
РисKSKOK=Непрерывная случайная потенциальная энергия=s (x)=EаFI=ее=

разбиение в=нулевых точках=Eсо случайными расстояниями=x между= нимиF= на одномерную цепочку случайных ячеистых= «потенциалов»= vl (бF=

=

ЗаметимI= что в двухJ= и трехмерном случаях все рассмотренJ ные выше обобщения оказываются несправедливыми из-за J воз можности обхода некоторого узлаK=

=

S.P.=Фазовое представление=

=

При изучении спектральных свойств системы нас интересуJ ют= стационарные= возбужденные состоянияI= волновые функции= которых удовлетворяют заданным граничным условиям на концах= цепочкиK=При этом циклические граничные условияI=когда цепочка= как бы соединяется в замкнутую петлюI= оказываются неудобными= для неупорядоченных системK=

NOO=

=

Более естественно считатьI= напримерI= что крайние атомы= неподвижны= EилиI= при рассмотрении электронного спектраI= что= волновые функции обращаются в нуль на концах цепочкиF=такI=что= амплитуды= uM = и= uk равны нулюK =Это можно рассматривать как= частный случай более общего условияI= согласно которому при= l = M и= l = k = степень возбуждения= zl =EтK=еK=отношение двух комJ понент= rl FI= должна принимать наперед заданные значения= zM и= zk =соответственноK=Из общей теории задач на собственные значеJ ния известноI=что если число=k достаточно великоI=то точные знаJ чения= zM и= zk I= как бы их ни выбралиI= мало влияют на спектрK= СледовательноI= можно без особой ошибки использовать простыеI= хотя и несколько нефизические условия= zM = M и= zk = M K==

С геометрической точки зрения эти условия означаютI= что=

при= l = M и= l = k	двухмерный вектор= rl									должен располагаться в=
заданном направленииK==
Рассматривая только=стационарное состояниеI=можно не обJ
ращать внимания на величины последовательных амплитуд Jвоз
бужденияI=а сосредоточиться лишь на исследовании фазы:=
					ì	u
					ïO~rctgE	l		F	для ESKNSFX
q º O~rctg	(	z	l	=	ï	ul-N				=	ESKOOF=
l				)	í	ul
					ïO~rctgE		F		для	ESKONFK
						¢
					ï
					î	ul

Фаза меняется вдоль цепочки от ячейки к ячейкеI= удовлетвоJ ряя при этом граничным условиям:=

	æ q		M	ö	æ q		k	ö
	tg ç			÷	= tg ç			÷	= M K====================ESKOPF=
		O				O
	è			ø	è			ø

Умножение на матрицу переноса= Τl эквивалентно вращению= вектора= rl K=Пользуясь соотношением=ESKNSFI=можно найти изменеJ ние фазы:=

ql +N - ql = hl Eql +NI lF ==================ESKO4F=

NOP=

=

через элементы матрицы= Tl иI= если аккуратно следовать алгебраиJ ческим формулам=ESKNTF=и=ESKOOFI=то можноI=начав с заданного знаJ чения= qM = M на одном конце цепочкиI=вычислить величину= qk =на= другом концеI=последовательно суммируя выражения=ESKO4FK=

Вообще говоряI= определенный таким путем конечный фазоJ

вый угол не будет удовлетворять граничному	условию= ESKOPF= на=
конце цепочкиK= Однако всякая матрица переноса	зависит	еще =от
спектральной переменной= lK= Последняя может входить в = Τl		либо=

явноI=как в формуле=ESKNSFI=либо по определению переменной=l=как=

энергия=«свободного электрона»= cO =в формуле=ESKONFK= Иначе говоJ ряI=конечную фазу надо написать в виде= qk ElF I=указывая на завиJ симость ее от= lK= Тогда спектр стационарных состояний системы= дается набором значений= lk I=удовлетворяющих условию=

qk ElF = Opk I= ESKORF=

где= k = –= целое числоK= Лишь для этих значений= l= можно одновреJ менно удовлетворить оба граничных условия=ESKOPFK=

Можно доказать общее положение:= если собственное значеJ

ние матрицы переноса вещественныI= то в спектре идеальной цеJ почки имеется=«запрещенная зона»K=

НапримерI= для регулярной модели Кронига= – Пенни можно= получить неравенство=

cosEc × x F +	N	×	dM	×sinEc × x	F >N I=	ESKOSF=
M	O		c	M
					утверждению:= в	одномерной цеJ
которое соответствует			обычному

почке дельта-функций с мощностью= dM I разнесенных на расстояJ

ния xM I= не существует стационарных состояний с энергией= cO =

(показать самостоятельноFK=

РазумеетсяI= здесь элементы матрицыI= переноса содержат пеJ риодическую функцию спектральной переменной= c K=СледовательJ

ноI= областиI= в которых удовлетворяется условие=ESKOSFI= выступают= как промежутки между различными= разрешенными зонамиK= Из=

NO4=

=

условия=ESKOSF=явствует такжеI=что эти запрещенные зоны сужаются= по мере роста= c K=

=

S.4.=Запрещенные зоны в спектрах== неупорядоченных цепочек=

=

Неупорядоченная цепочка= математически характеризуется= случайной последовательностью неодинаковых матриц переноса= T à I= произведение которых= ESKNTF= описывает распространение возJ

буждения= вдоль цепочкиK= Для каждой такой цепочки при помощи= численных расчетов можно= найти стационарные состоянияI= удоJ влетворяющие граничным условиям вида= ESKOPFK= Однако главная= задача состоит в отыскании спектрального распределения для анJ самбля цепочекI =в котором различные типы матриц переноса расJ пределены случайно с какими-то заранее заданными вероятностяJ миK=

NK= Наиболее прост пример случайного бинарного сплаваI= в=

котором матрицы переноса= TA и= TB =распределены вдоль цепочки= случайным образом с относительными концентрациями= cA =и= cB K=

OK=Все типы одномерного=«пространственного»=беспорядка=–= «одномерное стекло»I=«одномерная жидкость»=и тK=дK=–=можно опиJ сать единым образомI=последовательно выбирая матрицы переноса=

из множества= {T(x )}I= в котором задана функция	распределения=
m (x) межатомных расстояний= xK= НапримерI= теория	электронных=

состояний в= «одномерном жидком= металле»= основывается на изуJ чении цепочкиI=матрицы переноса для которой даются выраженияJ ми аналогичными=ESKONFK=При этом элементы матриц зависят от выJ бора чисел= x à на каждом шагеK=

Как отмечалосьI= в	спектре= периодической= цепочки имеется=
запрещенная зонаI= если	собственные значения матрицы переноса=
вещественныK= Пусть условие возникновения запрещенной зоны=
EORF= выполняетсяI= когда	спектральная переменная= c= принадлежит=

NOR=

=

области= L(x) (c )K=Для различных значений параметра= x I=(илиI=моJ

жет бытьI=для разных типов атомовF=указанные области будут разJ нымиK=

Допустим далееI =что все эти области в какой-то мере переJ

крываются:= существует область= { ( )I= общая для всех= (x) ( )==

l

L

l

L

при любых физически возможных значениях=x=Eили для всех сортов= атомов в сплавеFK= Тогда на каждом шаге вдоль любой неупорядоJ

ченной цепочкиI= построенной из матриц= {T(x )}I= возбуждениеI= коJ

торому отвечает спектральная переменная= lI= лежащая в области=

{

L(l )I=будет наталкиваться на матрицы перехода с=вещественными= собственными значениямиK= При этом вектор возбуждения=«застреJ

{

вает»K=Таким образомI= область= L(l ) оказывается запрещенной зоJ

ной в спектре любой цепочкиK=

В общем случае может быть доказана теорема:= любой облаJ

сти спектраI= которой отвечают запрещенные зоны в спектрах= как беспримесной цепочки типа I=Атак и беспримесной цепочки= типа ВI= соответствует и запрещенная зона в спектре решеткиI= построенной из произвольной смеси атомов А и ВK==

НапримерI= частоты колебаний изотопически неупорядоченJ ного сплаваI =представляющего собой смесь легких= EMF =и тяжелых= атомов= ENF= с массами соответственно= jM и= jN K= НапримерI= для= беспримесных цепочек из атомов типа=EMFI=фононный спектр имеет= вид:=

wO º l = O(ФjM )× (N - cos ObM K= ) ESKOTF=

Здесь константа Ф= выражается через силовые постоянныеI= а= величине= ObM =можно сопоставить волновой вектор возбуждения=qK=

Максимальная частота= w	=в этой зоне равна= éO(Ф j	ùN)O I=она=
m~x	ë	M û

лежит выше соответствующего предельного значения для бесприJ

NOS=

=

месной цепочки атомов с массами= jN K=Тогда из доказанной выше=

теоремы следует толькоI=что в смешанной цепочке запрещены чаJ стоты колебанийI= превышающие оба эти предельные значенияK= Иначе говоряI= не существует нормальных колебаний с частотойI= превышающей максимальную частоту колебаний периодической= цепочкиI=составленной из самых легких атомов смесиK=

Эта общая теорема применима и к=жидкости Кронига=–=ПенJ ниI= в которой одинаковые дельтообразные пики потенциальной= энергии= di = dM отстоят друг от друга на разных расстояниях= xi K=

ОказываетсяI= однакоI= что если отношение масс достаточно= великоI=то для некоторых волновых чисел возникают дополнительJ ные узкие запрещенные зоны в спектре фононовK=ДопустимI=прежJ де всегоI =что концентрация тяжелых атомов столь высока I =что= априорная= вероятность встретить длинную непрерывную последоJ вательность легких атомов очень малаK= Исключим произвольно из= статистического ансамбля все цепочкиI=в которых подряд располоJ жены более=E p -NF=атома массы= jM K=ТогдаI=любую неупорядоченJ ную цепочку можно рассматривать как случайную совокупность=

элементовI= выбранных из множества отрезков= {A(s )}= переменной=

длиныI=каждый из которых содержит один атом массы= jN =и=Es=JNF=

Z=MI=NI=OI=K=K=KI=EрJNF=атомов массы= jM K=Пусть= T(s ) (l )=–=матрица пеJ

реноса для такого отрезкаI=тогда в периодической цепочке из таких=

отрезков возникнет запрещенная зона= L(s ) (l )K Теорема утверждаJ етI= что в неупорядоченной цепочке также возникнет запрещенная=

{

зона в области= L(l )I= которая является общей для всех областей=

L(s ) (l )=при= N £ s £ p K СледовательноI=запрещенная зона в спектре=

рассмотренного ограниченного ансамбля неупорядоченных цепоJ чек может иметь вид как на рисKSKPK=

NOT=

=

=

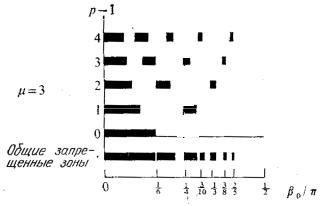
РисK=SKPK=Общие запрещенные зоны для сплавовI=не содержаJ щих более четырех легких атомовK=Отношение масс=–= jNjM = 4 =

=

Для совершенно неупорядоченной цепочкиI=в которой нельзя= полностью исключить вероятность обнаружения бесконечной поJ следовательности атомов только с массой= jM I= каждая из этих заJ прещенных зон должна быть в принципе бесконечно узкойK=Однако= более детальный анализ показываетI= что выше каждой исключенJ ной особой частоты лежит некоторая область настоящих уровнейI= соответствующих связанным=примесным модамK=Эти моды порожJ даются= «островками»= легких атомовI= отделенных друг от друга= «морем»=тяжелых атомовK=Островок из=р=легких атомов обладает=р= различными модамиK =Каждая из них уширяется в узкую зону за = счет взаимодействия=Eчерез тяжелые атомыF=с другими подобными= островками в цепочкеK=Результирующий колебательный спектр сиJ стемы представляет собой просто сумму всех таких вкладовK=ОднаJ коI= так как вероятность обнаружить цепочку с очень длинной Jне прерывной последовательностью легких атомов очень малаI= то= наблюдению доступно лишь несколько модI= лежащих непосредJ ственно под особой частотойK=Таким образомI=плотность состояний= в этой точке меняется почти скачком=EрисK=SK4FK=

NO8=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

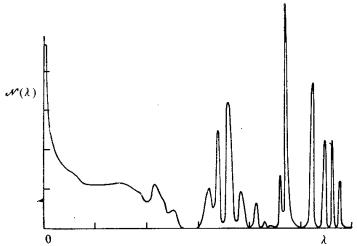
РисK= SK4K= Спектр неупорядоченной цепочки при отношении= масс атомов в сплавеI=равном трем=

=

Физическая интерпретация этого явления в рамках представJ ления об=«островках»=примеси наводит на мысльI=что похожие эфJ фекты можно наблюдать и в энергетическом спектре электронов в= неупорядоченных одномерных сплавахI=компоненты которых резко= различныK=НапримерI=в модели Кронига=– Пенни это означаетI=что= «силы»= дельта-функций= dl должны быть достаточно большими и =

достаточно сильно отличающимися друг от другаK==

=

S.R.=Плотность состояний=

=

Фазовое представление лежит в основе математической теоJ рии= плотности состояний= N (l) = = для возбуждений в цепочкеK= По=

определению= N (l)dl есть число дозволенных состояний= E«уровJ

ней»F=в интервале=ElI=l=H=dlF=в расчете на единичную ячейку цепочJ киK=Сама функция= N (l) определяется как пределI=к которому стреJ

NO9=

=

мится распределение уровней для одной цепочки при=k®=¥ или=Eв= неудобных случаяхF=как среднее по ансамблю таких цепочекK=

	Как отмечалосьI= новое					стационарное состояние		возникает=
	всякий разI=когда фаза= qk (l)					удовлетворяет условию=ESKORFK=Тогда=
	по определению=		N
	N (l )dl =	lim		×[qk El + dlF - qk ElF]I=				ESKO8JNF=
	или==	k ®¥ Opk
			N		¶qk ElF
	N (l )dl =	lim		×			K=	ESKO8JOF=
		k ®¥ Opk				¶l

Чтобы избавиться от вычисления производной от функцииI= которая может и не быть непрерывнойI= удобно ввести= интегральJ

ную плотность состоянийW=

l				N
D ElF = ò	¢	¢	= lim		× qk ElF I=	ESKO9F=
	N El Fdl

-¥

k ®¥ Opk

qk E-¥F = M K=

=

=

=

=

=

=

=

=

=

=

=

РисKSKRK= Интегральная плотность состояний в неупорядоJ ченной цепочкеI= в которой силовые постоянные распределены по= экспоненциальному закону=

=

NPM=

=