Дегтяренко Введение в физику неупорядоченных конденсированных 2011

Дайсон рассмотрел	модельI= в	которой силовые постоянные=
FlIl +N I= фигурирующие в	уравнении	колебанийI= подчиняются эксJ

поненциальному или гауссову распределениюK= В этом случае для=

интегральной плотности состояний удается получить аналитичеJ

ское решениеK =Для простоты изложения опустим выкладкиK =В реJ зультате получается плотность состояний = с«хвостом»I= простираJ ющимся в областьI =которая в упорядоченной системе была бы заJ

прещена=EрисK=SKRFK==

=

S.S.=Приближение локальной плотности=

=

Если функция распределения= m (x) непрерывно зависит от=

параметра беспорядка=xI=то спектр возбуждений можно найти приJ ближенноK= Если степень беспорядка не слишком великаI= то спектр= бесконечной цепочкиI= по-видимомуI= можно рассматривать как= сумму независимых вкладов от различных коротких отрезков Jце почкиI=концентрации компонентов сплава в которых различныK=ТаJ ким образомI= концепция=«островков»I= уже позволившая дать качеJ ственную трактовку происхождения особых частот и запрещенных= областей энергии в бинарном сплавеI=обобщается на предмет полуJ количественного описания полного спектраK=

Пусть требуется вычислить= EинтегральнуюF= плотность соJ стояний= a(λF= для неупорядоченной цепочкиI= в которой= среднее=

межатомное расстояние равно= x¥ K= В самом грубом приближении= можно взять плотность состояний для=регулярной=цепочки с таким= же межатомным расстояниемI=тK=еK=принять:=

D (l) »DM (lX x¥ ) K= ESKPMF=

Не следует думатьI=что такая оценка бесполезнаK=НапримерI=в= случае жидкости Кронига= – Пенни это приближение подскажет= намI=где искать главные=«разрешенные»=зоны и где могут быть заJ прещенные области энергииK==

Выберем теперь случайным образом конечный отрезок расJ сматриваемой цепочкиI= состоящий из= i= ячеекK= Если среднее межJ

NPN=

=

атомное расстояние в нем равно = xi I= то функция= DM (lX xi ) дает=

нам плотность состояний в идеальной цепочке с таким межатомJ ным расстояниемK= Будем далее рассматривать цепочку как послеJ довательность отрезков идеальной цепочкиK=Пусть длины этих отJ резков одинаковы и равны=iI=но средние межатомные расстояния в=

них= xi случайно изменяются от отрезка к отрезкуI= и вероятность=

реализации того или иного значенияxi задается функцией распреJ

деления= mi (		i ) K= Полученная			таким путем плотность				состояний=
	x
для всей совокупности отрезков называется=приближением локальJ
ной плотности:=
Di (l)= òmi (				i )×DM (lX		i )× d		i K=	ESKPNF=
			x		x		x
Эта аппроксимация дает						гораздо более точные			результатыI=

чем простая формула=ESKPMFK=Если функция= m (x) достаточно регуJ лярнаI=а длина=i=не слишком малаI=то функция распределения расJ

стояний= xi

удовлетворяет

центральной

предельной

теореме= и

стремится к гауссовой форме:=

ïì i (

i -

¥

O ïü )

i (

i

)

N

x

x

í

ý

I=

ESKPOF=

m

x

=

Opi × s

× exp

ï

-

OsO

ï

î

þ

где= sO есть средний квадрат флуктуации межатомного расстояния= при переходе от отрезка к отрезкуK==

Точная форма функции= DM (lXx) I= фигурирующей в формуле=

ESKPMFI=зависит от конкретных свойств данной физической системыK= Особенно интересныI= однакоI= те области спектраI= которые лежат= вблизи точекI= соответствующих краям зон в идеальной цепочкеK= Согласно теории функцийI= эти края зон должны совпадать =сосоJ

бенностями Ван ХоваK=

Рассмотрим простую задачу для плотности числа колебаний= в регулярной решетке с периодом= aK= Пусть= g – жесткость связей=

атомовI= имеющих массу= jK= Спектр колебаний определяется выраJ жением:=

NPO=

=

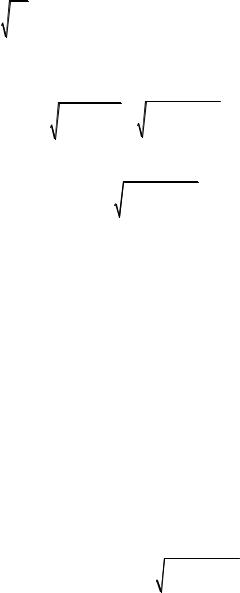
w = O

g

sin

ka

или== k =

O

~rcsin

w

K=

М

O

a

w

Тогда==

M

wMa

ka

dw =

cos

dk K=

O

O

Но так какK= cos

ka

O ka

(

O

)

M

=

N - sin

O

= N -

w L w

I=то можно сказатьI=

что=

O

O dw

N

= dk I=

a wM

N - (w L wM

O

)

т.еK=находим якобиан перехода от интегрирования по пространству=

æ dk ö

= k (w )K=

K к интегрированию по=w: ç

÷

è d w

ø

=

=

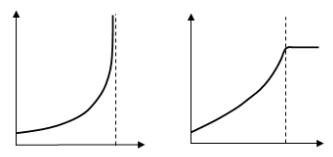
РисK=SKSK==Графики плотности числа состояний и интегральJ ной плотности состояний в одномерных системах=

=

=

Особенность Ван-Хова=EрисKSKSF:=

k EwF =	O		N		=
	a ×wM		N- (w L wM
				O	)

NPP=

=

(корневой характер плотности числа состояний в одномерных сиJ стемахI=в двухмерных системах=–==логарифмическая особенностьFK=

ИтакI= в одномерной регулярной решетке интегральная плотJ ность состояний вблизи потолка первой зоны приближается к едиJ нице по закону==

D (l ):N - (l		M	- l N O) ===для= =l= Y l		M	X			ESKPPF=
M						==
DM (l ):1===для= =l= [ lMK
Однако при	изменении			межатомного			расстояния=		i = точка=
								x

lM I=соответствующая потолку указанной зоныI= должна сдвигаться=

по какому-нибудь закону типа=
lС (xi )= l¥ + a(xi - x¥ )+ KKK I=	ESKP4F=

здесь= l¥ = – =потолок данной зоны для среднего= Eпо всей цепочкеF =

межатомного расстояния= x¥ I=а коэффициент= a определяется конJ

кретными параметрами моделиK= ПредположимI= что отклонения буJ дут малыI=поэтому оставим только линейный членK=

Подставляя соотношения=ESKPOF=–=ESKP4F=в формулу=ESKPNFI=поJ лучаем выражение для интегральной плотности состояний в неупоJ рядоченной цепочкеK=ИтакI==

ì		- l	N O	I l Y l
ïN- (l	M		)			M I=
DM (l )= í		NI		l	[l
ï						M
î

ì

N O

i (

n

)

ïN - él¥

+ a(xi - x¥ - lù)

lI x

í

ë

û I=

D%

=

ï

N

î

D%i

(l ): òe

-xO é

N O ù

êN - a + bx(

ú dx)I=

ë

û

где====== xO =

i

(

-

O I====== a = l

- l I== b = a

Os

K========ESKPRF=

x

i

x

¥

Os

¥

)

i

Под интегралом в= ESKPRF= стоит произведение двух функций:= плавной и с острым пикомK= Для интегрирования используем метод=

NP4=

=

перевала= –== в точке максимума плавная функция= fl (x) заменяется=

на= fl (A) и выносится за интегралI=а резкая функция интегрируетсяK=

НапримерI= достаточно далеко							в запрещенной			области энерJ
гии= Eвыше= l¥ F= обнаруживается							экспоненциально			затухающий=
хвост плотности состоянийI=описываемый выражением вида=
			(l-l¥ O)			(l-l¥		O)
-					-				×i
			bO			OsOaO				ESKPSF=
D (l ):N- e					=N - e				K=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
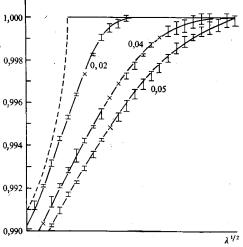
РисK= SKTK= Сравнение					интегральной плотности					состояний =в

модели= «жидкости»= Кронига= –= = ПенниI= вычисленной в приближеJ нии локальной плотности и путем расчета по методу МонтеJ Карло=

=

В действительности модель=«одномерной жидкости»=вряд ли= заслуживает столь утонченного расчетаI=хотя следует отметитьI=что= результаты таких вычислений совпадают с численными расчетами= по методу Монте-Карло=EрисK=SKTF=в пределах ошибкиK==

Таким образомI= метод приближения локальной плотности= очень полезен как эвристическийI= полуколичественный подход к=

NPR=

=

расчету спектра неупорядоченной системыK= Вместе с тем данный= подход по-видимому не может служить исходной точкой для строJ го определенного ряда последовательных приближенийI=сходящихJ ся к истинной плотности состоянийK=Это приближение совершенно= не годится для исследования= «патологических»= характеристик= спектра вроде особых запрещенных областей энергии в модели биJ нарного сплаваK=

=

S.T.=Квазиклассические электроны= в случайном потенциальном рельефе=

=

В случае=плотного газа=центров=Eисточников=слабого=рассеяJ нияF= потенциальная энергия электрона в поле каждого центра хаJ рактеризуется радиусом действия= rp K=Последний достаточно велик=

для тогоI= чтобы охватить много атомных сфер радиуса= rs I= однако=

глубина ямы здесь недостаточна для образования связанного J со стояния электронаK= Полная потенциальная энергия теперь предJ ставляет собой результат суперпозициимногих= перекрывающихся= вкладовI= и потому ведет себя подобно= гауссову случайному полюK= Будем считатьI=что среднее значение потенциальной энергии элекJ

r

трона в отдельном атоме равно нулю=–= V (o) = M K=ТогдаI=как и в=

разделе= «континуальный беспорядок»I= можно рассматривать велиJ

r

чину= V (o) как непрерывную случайную функциюI=значения котоJ

рой распределены с вероятностью=

N

ì

V

O

ü

P

(

V

=

exp

ï-

ï

=

ESKPTF=

OpW

ý

)

í

OW

O

ï

ï

î

þ

r

относительно единого начала отсчета энергии V (o) = M K=

Исходя из формы атомных потенциальных ям= vErrF I= можно= найти ширину распределенияI= W K Она получается из соотношения:=

NPS=

=

WO = u O	r	r r
	º k òu* (o)× u(o)× do K=		ESKP8F=

Вид потенциальной энергии электрона в поле отдельного= атома определяет также и автокорреляционную функцию:=

r		r r	r
	)=	uG (o + o¢)× u(o¢)		ESKP9F=
Г (o		u O	I=

с помощью которой можно найти бинарную функцию распределения=

N

æ

ö

mO ExNX xO X oF =

×exp

ç

-

xNO + xOO - OxNxOGEoF ÷

ESK4MF=

O é

O

N O

ç

(Op )p

O

éN - G

O

EoF

ù

÷

(Op )p

EoF

ù

ç

÷

ëN - G

û

è

ë

û

ø

r

и другие статистические характеристики поля= V (o)K==

В выражении= ESKP9F=для нас

существенно

тоI= что

функция=

r

GEoF удовлетворяет обычным предельным соотношениям и харакJ

теризуется=длиной корреляции=
i : rp :N gc I=	ESK4MF=

которая= i по порядку величины сравнима =с«радиусом действия»= каждого отдельного атомаK= Того же порядка будет и минимальная= длина волныI= соответствующая= спектральной области= M= Y= q= Y= qc = волновых чисел в фурье-представлении потенциальной энергииK=

Рассмотрим теперь электрон с энергией=bI=перемещающийJ

r

ся в случайном поле= V (o)K Если= b ? W I=то электрон всегда проJ

летает над горбами потенциального рельефаK=В этих условиях можJ но с достаточной точностью решить уравнение ШредингераI= расJ сматривая=s==как возмущениеI=искажающее волновые функции своJ бодных электроновK= Этот подходI= однакоI= неправомерен при более=

r

низких энергияхI= когда в некоторых областях величина= V (o) моJ

жет фактически превосходить= bK=Если рассматривать электрон как= классическую=частицуI=то при движении его на=«высоте»=b=над=«реJ

r

льефом»= V (o) он не сможет проникнуть под вершиныI=оказавшиJ

NPT=

=

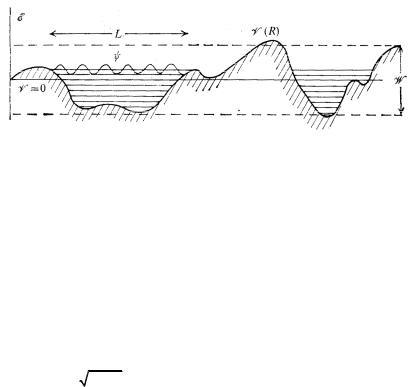
еся выше занимаемого им уровня= EрисK =SK8FK =Таким образомI =при=

решении уравнения= Шредингера важную роль будет играть= топоJ

r

графия= случайной функции= V (o)I= и результаты его решения = в

классическом предельном случае должныI= по принципу соответJ ствияI=согласовываться с ходом классических траекторийK=

РисK= SK8K= Квазиклассический электрон в случайном потенJ циале не способен проникнуть сквозь потенциальные барьеры=

=

Если на каждом отрезке классической траектории укладываJ ется много длин волн электронаI= то можно воспользоваться= кваJ зиклассическим приближением= для решения уравнения ШредингеJ

раK= В	рамках разумных допущений относительно						вида функции=
r	можно показатьI= что характерный размер= «топографических=
GEoF
		r	есть длина корреляции= iK= В типичной= «долине»= с=
деталей»= V (o)
«энергетической			глубиной»= W		квазиклассическое		приближение=
оправданоI= когда= i= превосходит					характерную	длину волны =де
Бройля= D »		h		I= тK= еKI= если воспользоваться		атомными единиJ
		OmW
цами= (h = m = e = N)I=когда выполняется неравенство==
	W iO ?N K=						ESK4NF=

В указанных условиях плотность состояний электрона с хоJ рошей точностью дается= приближением Томаса= –= ФермиW= в той= областиI=где потенциальная энергия электрона есть=sK=

NP8=

=

Плотность числа состояний= электронов выражается следуJ ющим образом:=

k (bIV ) : (b -V NO)K=

СоответственноI= интегральная плотность состояний= выраJ жается следующим образом:=

D (bIV	=)	N		éO(b -V	ùP) O K=	ESK4OF=
		Pp	O ë		û
Учтем теперьI=	что			значения=	V	распределены с вероятностью=

P (V )K= Поэтому интегральная плотность состояний с энергиейI= не= превышающей=bI=для системы в целом должна быть равна=

	N		b	éO(b - V ùP)		O × m (V )× d V K=
D EbF =			ò				ESK4PF=
		O
	Pp			ë	û
			-¥

СоответственноI= в квазиклассическом ность состояний электрона в случайном

ется выражением:=

b

kqc EbF = p-R L O × W-N × ò (b - V NL)O

-¥

	предельном		случае плотJ
			r
	гауссовом поле= V (o) даJ
	× expE-	V 2	F × d V K==ESK44F=
		OWO

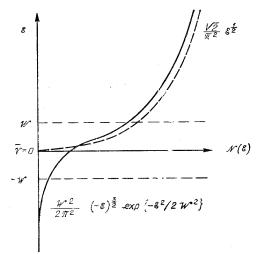
Поведение этой величины как функции энергии= Eее можно= выразить аналитически с помощью функции параболического циJ линдраF=изображено на рисK=SK9=сплошной кривойK=В области высоJ ких энергий= b ?W она приближается к обычной зависимостиI= характерной для свободных электронов=Eштриховая криваяFK=

kqc EbF »		O		× bN O K=							ESK4RF=
		pO
Однако при энергиях ниже уровняI= принятого нами за нулеJ
войI= плотность состояний не обращается в нульX= асимптотическиI=
при= b = -W I=она описывается выражением:=
		WO				-PL O	æ	V O ö
k	EbF »				×(-b	)	×exp ç -			÷ K=	ESK4SF=
			O
qc		Op					ç	OW	O ÷
							è		ø

NP9=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

=

РисK= SK9K= Плотность состояний в приближении Томаса= –= Ферми для гауссова случайного потенциала=

=

Иначе говоряI= у плотности состояний появляется модифиJ цированный гауссов= хвостI= отвечающий электронным уровням =в глубоких потенциальных ямахK=

В этом приближении кинетические характеристики электроJ

нов в рассматриваемой системе	определяются главным	образом=
темI= что классический электрон	не способен проникнуть	внутрь=
	r
любой областиI=в которой потенциальная энергия= V (o) превосхоJ

дит=bK==

Интуитивно ясноI= что при переходе от низких энергий к боJ лее высоким топология=«дозволенных»=областей должна изменятьJ сяK=Представим себе=«рельеф»I=заливаемый водойK=Для малых энерJ гий= b заполнены лишь самые глубокие минимумыI= образующие= изолированные= «пруды»= или= «озера»= EрисKSKNMFK= При таких значеJ ниях энергииI=следовательноI=все классические или квазиклассичеJ ские электроны будут= локализованыK= Однако с подъемом уровня=

N4M=

=