
Дегтяренко Введение в физику неупорядоченных конденсированных 2011
.pdfрой= «структуры»= средыK= Поэтому удобнее представить данные по= дифракции именно в этой формеI= чем производить сначала преобJ разование к функции= g (o) I=заданной в пространстве координатI=а= затем обратноK=
=
NNN=
=
РАЗДЕЛ=S= ВОЗБУЖДЕНИЯ В НЕУПОРЯДОЧЕННЫХ=
СИСТЕМАХ=
=
S.N.=Возбуждения в неупорядоченных системах=
Рассмотрим характерные колебательныеI= магнитные и элекJ тронные возбуждения в таких системахK= В описании этих возбужJ дений имеется много общих математических чертK=
NK == Фононная системаK ПустьI= напримерI= конфигурация сиJ стемы соответствует минимуму потенциальной энергииI=причем=à-й= атом располагается в точке= o à K=Как и в обычной теории колебаний=
решеткиI= допустимI= что при малом смещении этого атома= u à возJ
никают возвращающие силыI= линейные по относительным смещеJ ниям соседних атомовK= Тогда классические уравнения движения= для таких смещений запишутся в виде:=
KK |
r |
|
r |
ESKNF= |
|
j à ×u |
à = -åF àl¢ ×ul¢ K= |
|
|
l¢ |
|
Здесь= j à есть масса=à-го атомаI=тензор= F àl¢ описывает сиJ
лыI=возникающие в узле= o à при смещении атома в узле= olD K=
В периодической решетке одинаковых атомов силовые поJ
стоянные обладают трансляционной симметрией:= |
|
|
r |
r |
|
F àl¢ = F(oà |
- ol¢ )K= |
ESKOF= |
Тогда все=k уравнений=ESKNF=становятся эквивалентнымиI=пеJ реходя одно в другое при сдвиге решеткиK=Это свойство симметрии= позволяет упростить рассматриваемую систему уравнений с помоJ щью преобразования ФурьеK= В результате получаются фононные= моды кристаллаK =В неупорядоченных системахI =где различные коJ эффициенты могут быть случайными переменнымиI= такой общей= симметрии нетI=и уравнение=ESKNF=надлежит решать другими спосоJ бамиK=
NNO=
=
Простейший пример составляет случай идеального изотопиJ ческого беспорядкаI= когда массы= j à в эквивалентных узлах реJ
шетки не одинаковыK=ОчевидноI=это есть лишь очень частный слуJ чай беспорядка замещенияI= вместе с тем такой подход часто Jис пользуетсяI=чтобы описать влияние различия масс на динамику реJ шетки сплава замещенияK= В принципе надо было бы включить = в рассмотрение и корреляцииI= связанные с ближним и дальним поJ рядком в пространственном распределении различных типов атоJ мовK= Однако большое внимание уделяется и модели бинарного= сплаваI=в которой атомы типов=А и=В с массами= j A = и= j B распреJ делены в правильной решетке случайным образом K =Интересуясь в= основном спектром нормальных колебанийI= допустимI= что все= смещения= u à изменяются во времени с одной и той же частотой=wK=
Тогда систему=ESKNF=можно переписать в виде=
(F àà |
- wO × j à )×u à + å F àl¢ ×ul¢ |
= M K= |
ESKPF= |
|
l¢¹ à |
|
|
ОчевидноI= при наличии изотопического беспорядка |
изменяJ |
||
ются лишь |
диагональные элементы |
матрицыI= соответствующей= |
|
уравнениям=ESKPFK=Однако в настоящем сплаве=«химические»=разлиJ чия между компонентами приводят и к изменению силовых постоJ янныхI= что ведет к нарушению условия симметрии= ESKOFK= В этом= случае нельзя пренебречь и недиагональным беспорядкомK=
В общем случае= Eв жидкости или газеF =положения равновеJ сияI=характеризуемые векторами= o à I= не соответствуют периодичеJ
ской решеткеK= В такой системе не только все компоненты тензора= сил= F àl суть случайные величиныI=но даже само понятие= «близоJ
сти»= узла= à к данному узлу=l можно определить лишь статистичеJ скиK= Именно поэтому так трудно построить теорию возбуждений =в топологически неупорядоченных системахK=
OK=Магнитная системаK Благодаря известной аналогии между= фононами и магнонами сразу ясноI= что уравненияI= описывающие= отклонения спиновI=можно записать по образцу системы= ESKPFK=
NNP=
=

НапримерI= для спинового гамильтониана в условиях ферромагнеJ тизма можно записать=
pl Ez F £ p K= |
ESK4F= |
Воспользуемся гейзенберговским представлением и запишем= уравнения движения для каждого из операторов спиновых отклоJ нений=
p ±l = p E zFl ± i × p E yFl =
в следующем виде:=
ih |
¶p àE-F |
= -Oå |
égP ( àIl |
)× p àE-F × plE zF - g^ ( |
àIl )× pl E-F × p àE zF ù K= |
|
¶t |
||||||
|
l ¹ à |
ë |
|
û |
||
|
|
|
|
|
||
|
Если допуститьI=что все величины= p(à-) |
изменяются с одинаJ |
||||
ковой частотой= w и что система почти упорядочена= Eусловие= SK4FI = то получим систему уравнений=
éì |
|
|
ü |
ù |
|
|
|
|
ï |
|
( àIl |
ï |
- hwú × p Eà-F - Op å |
ég^ ( àIl |
)× plE-F ù |
= M KESKRF= |
|
êíOp å gP |
ý) |
|||||||
êï |
l ¹ à |
|
ï |
ú |
l¹ à |
ë |
û |
|
ëî |
|
þ |
û |
|
|
|
||
Эта система уравнений аналогична по структуре системе=ESKPFK=
PK= Электронная системаK Вполне естественноI= что похожие= уравнения получаются и при описании электронных состояний= конденсированной среды в модели= сильно связанных электроновK= Пусть потенциальная энергия электрона в изолированном=à-м атоме=
есть= v à (rr) K= В |
этом поле существуют атомные уровни энергии= |
b(àa) I= которым |
соответствуют различные= атомные орбитали= |
y(àa) (rr )K= Допустим далееI= что потенциальная энергия электрона в=
рассматриваемой системе дается просто суммой энергийI=которыми=
он обладал бы в системе отдельных атомах:=
r
r (rr ): åv à (rr - o à )K============================ESKSF=
à
NN4=
=
Тогда естественно предположитьI=что решение уравнения ШрединJ гера==
ì |
O |
|
|
ü |
|
|
|
|
|
|
ï- |
h |
×ÑO +r |
( |
rr ïY rr |
= E × Y rr |
= |
( |
) |
ESKTF= |
|
|
||||||||||
í |
Om |
|
)ý |
( |
) |
|
|
|||
ï |
|
|
ï |
|
|
|
|
|
|
|
î |
|
|
|
þ |
|
|
|
|
|
|
можно представить в виде линейной комбинации атомных орбитаJ лей=EЛКАОF:=
r |
EaF |
EaF |
r |
r |
ESK8F= |
|
Y(r )= åu à |
×y à |
(r - o à )K= |
||||
|
àIa |
|
|
|
|
|
Подставляя |
разложение= ESK8F= в уравнение= ESKTF= и используя= |
|||||
|
|
|
EaF |
r |
r |
и= |
свойства атомных орбиталейy à |
(r - o à )= Eортогональность |
|||||
нормированностьFI= получаем |
систему |
линейных уравнений |
для= |
|||
определения коэффициентов=uK= |
|
|
|
|
||
Для больших систем различные интегралы перекрытияI= вхоJ дящие в эти уравненияI=сложны и неопределенныK=Они могут быть= вычислены из первых принципов только численными методами = с использованием принципа минимизации полной энергии системыK= Иногда используют упрощенную форму указанных уравнений:=
(b(àa) - E)×u(àa) + åås àl(ab) ×ul(b) = M K= |
ESK9F= |
l¹ à b |
|
Здесь матричные элементы= s àl(ab) модельного гамильтониаJ
на подбираются эмпирически с таким расчетомI= чтобы воспроизвеJ сти структуру электронных зон в данном кристаллеK= Отметим еще= раз близкую аналогию между полученными уравнениями и системой= ESKPFK==
== ИтакI== можно сказатьI=что уравнения=ESKPFI=ESKRFI= ESK9F=имеют= один и тот же вид:=
(b à - l)×u à + ås àl ×ul = M =============================ESKNMF=
l ¹ à
(здесь=a=–=фиксированоI=рассматриваем одну энергетическую зонуFI= где переменная= u à соответствует амплитуде возбуждения на= à-м=
NNR=
=
узлеI= а переменная=lI= характеризующая спектр возбужденийI= соотJ ветствует:=
J=либо квадрату частоты колебаний= wO I== J=либо энергии=hw магнона или экситонаI==
J=либо собственному значению энергии= b=электронного гаJ мильтониана всей системыK==
Статистические характеристики диагональных элементов= b à =
и недиагональных элементов= s àl можно установитьI= сопоставляя=
системы уравнений=ESKPFI=ESKRF=или=ESK9FK=В задаче о колебаниях реJ шетки такое сопоставление дает=
b à ® j -à NF àà I==s àl ® j -à NF àl K= |
ESKNNF= |
Если=«исходные»=узлы образуют периодическую решеткуI=то= естественно заменить индекс= à= вектором решетки= o à K= В упорядоJ
ченной системе энергия= b à = не зависела бы от= àI= а величины= s àl =
удовлетворяли бы условию трансляционной симметрии= ESKOFK= При= этом уравнения=E9F=можно было бы сразу решитьI=пользуясь теореJ
мой Блоха= u à = åwEqF ×eiqo à K= Совершив преобразования ФурьеI=
получим:=
é |
|
à |
|
å) |
|
( |
r |
ê( |
e |
- l + |
s |
h |
|||
ê |
|
|
|
||||
ë |
|
|
|
h¹M |
|
|
|
×)e |
rr ù |
r |
|
|
iqh |
ú |
ESKNOF= |
||
|
× w(q )= M K======== |
|||
úû
Параметр= l здесь оказывается собственным значением матJ рицы в правой части выраженияK==
При рассмотрении колебаний решетки это является обычной=
динамической матрицей для квадратов частот= éw(q )ùO |
= нормальJ |
|
ë |
û |
|
ных колебаний с волновым вектором=qK==
В простейшей модели металла с сильной связьюI=когда кажJ дому узлу соответствует один атомный уровень энергииI= получим= типичную зону разрешенных состояний с энергиями=
NNS=
=
r |
r |
rr |
|
iqh |
K====================ESKNPF= |
||
l(q )= bM + ås (h )× e |
|
||
h¹M
r
Если=«интеграл перекрытия»=s (h )=отличен от нуля лишь для=
ближайших= z= соседей данного узла= Eон тогда равен= sFI= то центру= зоны соответствует энергия= bM I=а полная ширина зоны дается выJ ражением=
OB = Ozs I=================================ESKN4F=
где В=–=ширина зоныK=
Энергия электрона в зоне достигает минимума и максимуJ мов соответственно в центре=Eq=Z=MF=и на границах зоны БриллюJ энаK=Параметр В удобно использовать в качестве энергетического= масштаба системыW= он характеризует величину взаимодействия= между соседними узлами решеткиK==
РазумеетсяI= сделанные замечания совершенно тривиальны с= точки зрения обычной физики твердого телаI=а модель электронной= или фононной зоныI= записанная в виде= ESKNPFI= очень далека от= настоящих системK==
Однако в теории неупорядоченных систем зачастую только= такие простые модели и удается рассматривать с известным успеJ хомK=
=
S.O.=Возбуждения в одномерных системах==
=
Рассмотрим возбуждения в неупорядоченной одномерной= цепочкеK==
NK Диагональный беспорядок уровней энергии= e à и недиаJ
гональный беспорядок матричных элементов= s àl потенциальной=
энергии могут быть связаны с двумя причинами:==
- во-первыхI=могут иметь место физические или химические= различия между компонентами периодически расположенных ячеJ ек периодической цепочкиX=
NNT=
=
- во-вторыхI=возможны флуктуации относительных расстоJ яний= x à между атомными центрами в цепочкеI=а беспорядок полуJ
чается как следствие этих флуктуацииK==
OK Наиболее серьезное ограничение полезности одномерных= моделей с теоретической точки зрения связано с обязательной тоJ пологической их упорядоченностьюK=Это означаетI=напримерI=что= «индекс узла»=à=в уравнениях=ESKNMF=всегда эквивалентен=«вектору»= периодической решеткиI=в которой среднее межатомное расстояние= такое жеI=как и в настоящей системеK==
Говоря математическим языкомI= нет возможности отлиJ
чить беспорядок замещения в=«одномерном сплаве»=от эффектовI= связанных со случайным характером расстояний между атомами= в=«одномерном стекле»= или=«одномерной жидкости»K Физические=
допущенияI=лежащие в основе моделиI=влияют лишь на статистичеJ ские характеристики величинI= фигурирующих в качестве диагоJ нальных и недиагональных элементов в уравнениях=ESKNMFK=
PK= Неизбежность последовательности атомов=Eв случае одноJ мерной моделиF=позволяет сформулировать==другой поход к поиску= метода решения уравнений=ESKNMFK=
Мы не сильно потеряем в общностиI= если допустимI= что веJ личины= s àl отличны от нуля лишь для ближайших соседейK=Тогда=
система=ESKNMF=принимает вид:= |
|
(el - l)ul +slIl+Nul+N +slIl-Nul -N = M K= |
ESKNRF= |
Введем матрицу переносаI= которая генерирует |
последоваJ |
тельные дифференциальные уравнения вида=ESKNMFK= |
|
æ ul |
ö |
|
é |
|
M |
= |
ê |
|
s |
||
ç |
÷ |
|
ê |
|
lIl -N |
èul+N ø |
|
ê |
- |
|
|
|
s |
||||
|
|
|
ë |
|
lIl +N |
|
N |
úù |
æul -N ö |
r |
$ |
r |
||
- |
el - l ú ×ç |
ul |
÷ |
==или=rl+N = Tl ×rl K= = ESKNSF= |
||||
|
ú |
è |
ø |
|
|
|
||
|
|
|
|
|||||
|
|
|
|
|
||||
|
slIl +N û |
|
|
|
|
|
|
|
NN8=
=
r |
æ |
u |
ö |
=–==вектор амплитуд двух соседних ячеек= |
Здесь= rl +N º çu l |
÷ |
|||
|
è |
l+N ø |
|
|
r |
æul -N ö |
= – = =амплитуды в предыдущей паре узJ |
||
lIl +N I =а вектор= rl º ç |
u |
÷ |
||
|
è |
l |
ø |
|
ловK=
r
Отсюда следуетI=что возбуждение= rl в= l -м узле порождается= соответствующим возбуждением в предыдущем узлеI=умноженным=
на матрицу переноса= T$l-N K= В простейшем случае= T$l =–=это матрица= O=×=OI=компоненты которой даются выражением=ESKNSFK==
Таким образомI=матрица переноса однозначно связана с кажJ дой ячейкой решеткиK= Распространение возбуждения вдоль цепочJ ки можно изобразить в виде матричного произведения последоваJ тельности соответствующих матрицK= Пользуясь соотношением= ESKNSFI=получаем:=
r |
$ |
D |
-N |
$ |
$ |
r |
ESKNTF= |
|
rl+l¢ = Tl+l¢ |
×Tl+l¢-O ×KKKTl¢ ×rl¢ K= |
|||||||
Для упорядоченной |
системыI= в |
которой все матрицы переJ |
||||||
носа одинаковыI=можно записать= |
|
|
|
|||||
|
r |
é$ù l |
|
r |
|
|
|
|
rl+l¢ = |
ëTû |
|
×rl¢ K=================================================ESKN8F= |
|||||
Влияние беспорядка сводится к томуI=что матрицы переноJ са меняются от ячейки к ячейке за счет случайных вариаций элеJ
ментов матрицы=ESKNSFK=Другими словамиI=матрица переноса= T$ есть= случайная функция номера узла= l X=функция распределения ее знаJ чений определяется физическими особенностями данной моделиK==
Рассмотрим более конкретную задачу о движении электроJ на в поле одномерного случайного потенциалаI=имея в виду беспоJ рядок замещенияI=можно построить модель сплава Кронига=–=ПенJ ни=EрисK=SKNI=аFK=Узлам решетки в этой модели приписываются дельJ тообразные потенциалы с различными=«силами»= dl K=
NN9=
=
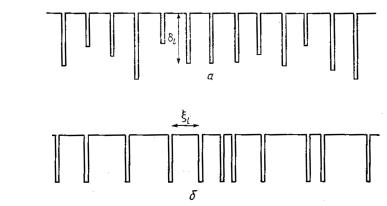
Можно |
ввести и |
|
модель |
жидкости |
Кронига= –= Пенни= |
||
(рисKSKNIбFI= в |
которой случайной переменной служит расстояние= = |
||||||
между соседними дельта-функциями xN K== |
|
|
|||||
В обоих случаях обычная теория модели |
Кронига= –= Пенни= |
||||||
для периодической цепочки подсказывает намI= что решение уравJ |
|||||||
нения Шредингера при |
энергии= b = cO строится из |
волновых= |
|||||
функций свободного электрона с волновыми числами= ±c K= |
|
||||||
Пусть |
координата= x |
принадлежит= l-му= «открытому |
промеJ |
||||
жутку»= E M £ x £ xl FK= Тогда |
указанную |
функцию можно записать =в |
|||||
виде:= |
|
|
ul¢ |
|
|
|
|
|
|
|
|
|
|
||
yl ExF = ul × cosEc × xF + |
|
×sinEc × xF K= |
|
ESKN9F= |
|||
|
|
||||||
|
|
|
c |
|
|
|
|
=
=
 =
=
=
==
=
=
=
=
=
=
=
 =
=
=
РисKSKNK= = Модели Кронига= –= ПенниW= а= –= «сплав»X= б= –= «жидJ кость»=
=
Коэффициенты здесь пока произвольныK= Однако функцию=
ESKN9F= по |
прохождении |
через сингулярность= dl надо= «сшить»= с= |
волновой |
функцией= yl+N |
из соседнего промежуткаK =Условия сшиJ |
вания при таком переходе имеют вид:=
NOM=
=
