Дегтяренко Введение в физику неупорядоченных конденсированных 2011

T.9.=Роль размеров системы=

Ранее подчеркивалосьI=что понятие порога протекания имеет= смысл лишь в бесконечной системеK= В конечной системе порог= протекания меняется от образца к образцуI=т.еK=является величиной= случайнойK= ОднакоI= значенияI= которые принимает эта случайная= величинаI= с подавляющей вероятностью попадают в некоторую= область с шириной= d(η) I= которая называется= критической облаJ

стьюK=При увеличении числа узлов в системе= h ширина этой облаJ сти уменьшается по степенному законуI= так что при= h ® ¥ порог=

протекания приобретает четкий смыслI= превращаясь из случайной= величины в величину достовернуюK==

Рассмотрим эксперимент с экранной сеткойI= имеющей разJ меры=i=×=iI=схема которого изображена на рисKTKONK= ДопустимI=что= сделано много опытовI=использующих разные случайные последоJ вательности блокируемых узловI= результатом которых явился= набор порогов протеканияK=НапомнимI=что конфигурации блокироJ ванных узловI= полученные в разных опытахI= совершенно не похоJ жи друг на другаK==

Удобный способ рассуждения состоит в следующемK=ВообраJ зим= бесконечную экранную сетку с заданной долей= x неблокироJ ванных узловK==

ПредставимI= что на разные участки этой сетки накладываетJ ся:=квадратI=имеющий размеры=i=×=iI=и изучается протекание с леJ вой стороны этого квадрата на правую по неблокированным узламI= оказавшимся внутри этого квадрата=EрисKTKONFK=Накладывая квадрат= на разные участки бесконечной сеткиI=можно перебрать результаты= разных опытов с конечной сеткойK==

В бесконечной экранной сетке протекание возникает точно= при=x=Z=xcI=ноI=как можно увидетьI=это совершенно не означаетI=что= при=x=[=xc обязательно есть протекание в квадрате=i=×=iK==

При= x= [= xc в бесконечной системе существует бесконечный= кластерK=Изобразим его скелет в виде рыболовной сетиI=показанной= на рисKTKONK= Для дальнейшего крайне важно соотношение между=

NTN=

=

радиусом корреляции=o и длиной квадрата=iK=Примем сначалаI=что= i значительно превосходит=oK=Тогда=EсмK=рисKTKONF=внутри квадрата= находится много ячеек сети бесконечного кластераI= который обесJ печивает протекание между сторонами квадратаK=Эти ячейки могут= иметь разные размерыI =в сети бесконечного кластера могут быть = большие дырыI= но если в квадрате в среднем должно быть много= ячеекI=то вероятность тогоI=что в кластере имеется дыра размером в= целый квадратI= ничтожно малаK= Поэтому делается следующий выJ

вод:= ENF= Если= x= [= xcI= то порог протекания квадрата не может= находиться в области значений= xI= удовлетворяющей сильному неJ равенству=i=[[=oExFK=Эта область должна быть выше порогаK=

Согласно формуле=ETK8F=при стремлении=x к=xc радиус корреJ ляции неограниченно возрастает и при каком-то значении= x неизJ бежно сравнивается с=iK=Теперь о протекании внутри квадрата ниJ чего определенного сказать нельзяK= Все зависит от конкретной= конфигурации блокированных узлов внутри негоK==

=

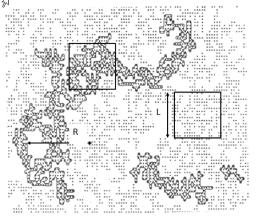
РисK= TKONK= Большие кластерыI= заданные компьютером на= квадратной решетке при=p=Z=MIRPI=т.еK=ниже порога протекания по=

узлам= E pcp = MIR9F K= Эти кластеры соединены в основном одноJ

кратно=

=

NTO=

=

Пусть теперь= x= Y= xc и радиус корреляции значительно меньJ шеI=чем=iK=При=x=Y=xc и радиус корреляции представляет собой макJ симальную длину конечных кластеровK=Если= o= YY= iI =то не сущеJ ствует такого кластераI=который мог бы связать стороны квадратаK==

Поэтому делается еще один определенный выводK==

EOF= Если=x=Y=xcI=то порог протекания квадрата тоже не моJ жет находиться в области значений=xI=удовлетворяющей сильному=

неравенству=i=?=oExFK=Эта область должна быть ниже порогаK=

Если=x=Y=xc=I=но величина=x очень близка к=xcI=то радиус корJ реляции становится большеI= чем= iK =В этом случае о протекании в= квадрате нельзя сказать ничего определенногоK= В бесконечной сиJ стеме существуют конечные кластеры размераI=большегоI=чем=iI=но= внутри них есть дыры такого же размераI=и все зависит от конкретJ ной конфигурации блокированных узлов внутри квадратаK==

Теперь можно оценить размер критической области в котоJ рой могут находиться значения порога протекания квадрата=i=×=iK= Согласно выводам=ENF и=EOF эта область должна определяться услоJ вием=i ≤=oK=Как видно из рисK=TKOMI=чем больше=iI=тем уже эта обJ ласть и тем теснее она прижата к порогу протекания для бесконечJ ной системыK=Ширина области==определяется условием=o(δF=Z=iK=С=

помощью формулы=ETK8F=получаем= l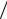dn =Z=i или==

d = (l L i NL)n .	ETK9F
Внутри критической областиI=т.еK=при=|x=–=xc|=пороги протекаJ
ния квадратов с длиной= i распределены	однородноK= Точка= x= Z= xc=

внутри этой области ничем не выделенаK=ДействительноI=это точкаI= в которой наступает протекание в бесконечной системеK=Но устаноJ витьI=есть такое протекание или нетI=работая с квадратом конечноJ го размераI=невозможноK=Если=i=Y=oI=то накладывая квадрат на разJ ные участки бесконечной сеткиI=нельзя сказатьI=существуют в этой= сетке только конечные кластеры или они уже слились и образуют =

бесконечный кластерK= Изучение протекания в квадрате конечного= размера позволяет лишь определить ширину критической областиK==

NTP=

=

В этом разделе обсуждались лишь плоские задачиK= Однако= все сказанное полностью переносится на задачи объемныеK= ШириJ на критической области для объемных задач также определяется= формулой=ETK9FK= Небольшая разница возникаетI= если выразить шиJ рину δ не через размер системы= iI= а через полное число узлов= h K=

Дело в томI =что= h = (i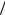a d)I= где= a= – =период решеткиI =d= –= размерJ ность пространстваK=Поэтому согласно=ETK9F==

d(h )= ` I======================================ETKNMF=

hNL n

где= `= –= численный коэффициентI= который не может быть опредеJ лен из столь простых соображенийK= Именно с помощью этой форJ мулыI= в результате исследования найденной на ЭВМ зависимости=

d(h) I=был впервые определен индекс радиуса корреляции плоской=

задачиK=ОказалосьI=что= nO Z=NIPPK=Eчисло=O=–=индекс двухмерной сиJ стемыKF=Для трехмерных задач индекс= n иной:= nP =Z=MI8=÷=MI9K==

=

T.NM.=Электропроводность вблизи порога протекания=

=

Рассмотрим двухмерные или трехмерные сетки с блокироJ ванными узламиK= Как говорилось в начале главыI= электропроводJ ность таких сеток отлична от нуля при=x=[=xc и обращается в нуль= на пороге протекания=xcK=Экспериментальные данныеI=а также данJ ныеI= полученные с помощью расчета на ЭВМI= показываютI= что= удельная электропроводность сеток обращается в нуль по закону==

s(x )= sM (x - xc t I===============================ETKNNF=)

где множитель= sM по порядку величины равен удельной электроJ проводности сетки без блокированных узловK=Величина=t называетJ

ся=критическим индексом электропроводности и является предмеJ

том очень тщательного изученияI= преимущественно с помощью= расчетов на ЭВМK=EВ одном из последних расчетовI=напримерI=исJ пользовалась квадратная сеткаI= имеющая= 8MM= ×= 8MM= узловKF= УстаJ

NT4=

=

новленоI=что для двухмерных сеток= tO =Z=NKPI=а для трехмерных== tP =

Z=NKS=÷=NKTK==

Сеточная модель бесконечного кластера позволяет вывести= формулу=ETKNNF=и связать индекс=t с индексом радиуса корреляцииK= Электрический ток течет только по бесконечному кластеруI=причем= именно по его скелетуK=В мертвых концахI=прикрепленных к скелеJ ту лишь с одной стороныI=тока нетK=Если сделать электрический ток= достаточно сильнымI= так чтобы проволокаI= по которой он течетI= светиласьI= то в темноте скелет бесконечного кластера можно= наблюдать визуально освещенные каналы на темном фонеK= Вдали= от порога вся сетка светится более или менее равномерноI= вблизи= порога расстояние между освещенными каналами увеличивается иI= наконецI= на самом пороге свечение совсем прекращается=–=ток чеJ рез систему прервалсяK==

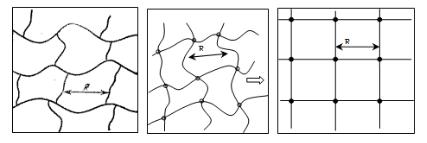
Вычислим удельную электропроводность скелета бесконечJ ного кластераK=Следует иметь в видуI=что это вычисление не может= претендовать на правильный учет численных множителейK= Оно= позволяет лишь получить зависимость= s от=x=–=xcK=Эта зависимость= не изменитсяI=если мысленно заменить неправильную и нерегулярJ ную сеть идеальной сеткой с I=периодомравным= oK=

=

РисK=TKOOK=К оценке проводимости скелета бесконечного кластера=

=

Рассмотрим сначала плоский случай=EрисKTKOOFK=Удельное соJ противление равно сопротивлению квадрата с единичной длинойK= Число проволочекI= пересекающих этот квадратI=равно=NLoI= где= o= –= расстояние между проволочкамиI= которое выражается формулой= ETKTFK=Обозначим сопротивление одной проволочкиI=имеющей едиJ

NTR=

=

ничную длинуI= через= rM K= Все проволочки включены параллельноK= СледовательноI=удельное сопротивление=

r = NLrMo = rM × o I=

а удельная электропроводность==

s = r-N = r-MN × o-N K========================ETKNOF==

Подставляя=ETK8FI=получим==

s = sO (x - xc n )I=========================ETKNPF=

где= sO = r-MN ×l -N K==

В трехмерном случае нужно вычислить удельное сопротивJ ление проволочного каркасаI= изображающегоI= напримерI= простую= кубическую решетку с периодом=o=Eот типа решетки зависит лишь= численный коэффициентFK= Удельное сопротивление равно сопроJ тивлению кубика с единичной длиной ребраK= Число параллельно= соединенных проволочекI= проходящих через грань такого кубикаI= равно=NLoOK=Поэтому удельное сопротивление==

r =

rM

= r

M

× oO

==============================ETKN4F=

(NL o O)

и удельная электропроводность равна:=

On)I=========================ETKNRF=

s = r-N × o

-O = s

P

(x - x

M

c

где= s

P

= r-N ×l-O K==

M

Следует обратить внимание на тоI= что удельная электропроJ

водность= s в

двухмерном

и

трехмерном случаях имеет разную=

размерностьK= В

двухмерном

случае

она

измеряется в

–N

ОмI =а в=

трехмерном=–=в Ом–N·см–NK==

Множители= sO и= sP по порядку величины представляют соJ бой удельные электропроводности двухмерной и трехмерной сеток= без блокированных узловK=ДействительноI= как видно из формул= ETKNOF= и=ETKN4FI= удельная электропроводность= sExF превращается в =

sO или в= sP при=o=Z=lI=т.еK=когда сетка бесконечного кластера совJ

NTS=

=

падает с исходной сеткойI=на которой ставится задачаK=Таким обраJ зомI=величина= sM в формуле=ETKNNF=в двухмерном случае равна= sO I= а в трехмерном=–= sP K==

Сравнивая формулы= ETKNOF= и= ETKNPF= с формулой= ETKNNFI= полуJ чаемI= что в двухмерном случае= t = n I= а в трехмерном= t = On K= ИсJ

пользуя= nO =NIP и= nP = MIS ¸ MI9 I= получим= tO =NIP I= tP =NIS ¸NI8 I=

что очень близко к приведенным выше даннымK= Это совпадение= свидетельствует в пользу модели Шкловского=–=де ЖенаK==

=

T.NN.=Мощность скелета бесконечного кластера= вблизи порога протекания.=Роль мертвых концов=

Как и электропроводностьI= функция= mExFI= представляющая= долю узловI=принадлежащих бесконечному кластеруI=обращается в= нуль при= x= Z= xcK= Исследования показалиI= что вблизи порога эта= функция имеет вид==

mExF = aEx - xc Fb I==================================ETKNSF=

где=a=–=численный коэффициент порядка единицыI=а= b =–=еще один=

критический	индексK= УстановленоI= что для двухмерных задач=
bO = MIN4 I= а	для	трехмерных= bP = MI4 K= Эти результаты получены=
главным образом		с помощью ЭВМK==

Вфункцию=mExF=дают вклад все узлы бесконечного кластера=–=

ипринадлежащие скелетуI= и принадлежащие мертвым концамK= С= помощью модели бесконечного кластера можно определитьI=каких=

узлов большеK=Допустим сначалаI= что мертвых концов совсем нетI=

ивычислим вклад в=mExF=от скелета бесконечного кластераK==

Вдвухмерном случае на каждую ячейку бесконечного кластеJ ра приходится порядка=oLa узловI= принадлежащих скелетуI= где=a= –= период решетки=Eкак и в предыдущем разделеI=здесь делается оценJ каI=не претендующая на установление численных коэффициентовFK=

Площадь ячейки порядка= oO иI=следовательноI=полное число всех=

NTT=

=

узлов в ячейке порядка= oO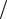aO K =Отсюда следуетI =что доля узловI = принадлежащих скелету бесконечного кластераI==

mск (x ): oa : (x - xc n )K=============================ETKNTF=

Здесь знак=«~»=означает равенство по порядку величины=Eбез= учета численных коэффициентов порядка единицыFK==

В трехмерном случае на каждую ячейку бесконечного клаJ стера тоже приходится= EoLaF= узловI= принадлежащих скелетуI= но= полное число узлов в ячейке порядка=EoLaFPK=Поэтому в трехмерном= случае==

mск (x ): (

a

)O : (x - xc

On) K==========================ETKN8F=

o

Сравнивая

формулы= ETKNTF= и= ETKN8F= с

формулами= ETKNPF= и=

ETKNRFI=можно видетьI=что доля узловI=принадлежащих скелету бесJ

конечного

кластераI= по

порядку

величины

совпадает

с функцией=

s(x )s

M

=

(x - x

t K==)

c

Сравнивая=ETKNTF=и=ETKN8F=с формулой=ETKNSFI=видимI=что==

mск (x)

nO -bO

mск (x)

OnP -bP

: (x - x

)

=========и========

: (x - x

c

)

=

m (x )

c

m (x )

в двухмерном случае и трехмерном случаях соответственноK==

ВспомнимI=

что=

nO =NIP I=

а= nP » MI9 K= СледовательноI=

nO -bO =NIO I=~= OnP - bP »NI 4 K=Таким образомI=и в двухмерномI=и в=

трехмерном случаях отношение= mск (x)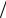m (x) быстро стремится к=

нулю при=x →=xcK=Это значитI=что узлыI=образующие скелет бескоJ нечного кластераI= составляют ничтожную долю от полного числа= узловI= принадлежащих бесконечному кластеруK= Основная= «масса»=

бесконечного кластера сосредоточена в мертвых концахи соверJ

шенно бесполезна с точки зрения электропроводностиK= Поэтому= вблизи порога протекания= s(x)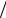sM = m (x)K= Однако именно мертJ

вые концы определяют спонтанную намагниченность ферромагнеJ тика с примесями вблизи порога протеканияK=

NT8=

=

РАЗДЕЛ=8= ТЕОРИЯ ПРЫЖКОВОЙ ПРОВОДИМОСТИ==

=

Прыжковой проводимостью называют перенос тока за счет=

перескоков носителей между локализованными состояниямиK= Это=

явление можно наблюдать в полупроводниках с примесями и= в

аморфных

телахI=

в

которых

она

существует

в

большом=

температурном

интервале= EM= ÷= NM= КFI= в

полупроводниках

этот=

температурный

интервал= –= EM= ÷= N= КFK= Обычно

рассматриваются=

четыре

температурных

интервала

для

проводимо=

полупроводниковK=

зоной= Dbg =

NK= В

чистом

полупроводнике

с запрещенной

-

DEg

удельная

электропроводимость= = = =

s » s

Ohq I= что

означает=

×e

N

заброс через зонуK=

M

OK= При комнатной температуре и более низких температурах===

ET= YY= Dbg F =эта часть не проявляетсяI =и на первое место выходит=

наличие

примесейI=

которые

создают

локальные

уровни=

в

запрещенной

зонеK=

Отдельный

атом

можно

характеризовать=

энергией

ионизации=

= и

размером

волновой

функции

внешнего=

электрона==

bG =NPKS ×

æ

m*

ö

× N

I======== аG = MIRP´NM-8 ´ eæ

m

ö I=

B

ç m

÷

e

Б

14243

ç

*

÷

è

ø

aM

è m

ø

Б

где= e »NM ¸NR I= m* » MINme K=

мала= kd (aB* )P =NI=

Если

концентрация

примесей

то=

примесное состояние сохраняет свою индивидуальностьK=

æ

-b

O

ö

s » sOM

exp ç

÷ I=

hq

è

ø

где= bO ~ MIN¸ MIMN эВ=Eсотни градусовFK=

NT9=

=

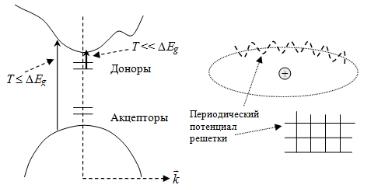
Проводимость	таких	слаболегированных	= систе
осуществляется за счет	заброса	электрона в зону проводимости=
(рисK8KNFK=
=

РисK8KNK= Проводимость за		счет заброса		=
			электронов в зону=
проводимости=
=		q= YY= bO
PK= При	температурах=		такие	процессы=

«вымораживаются»=и существенным становится вклад от прыжков=

	электронов	по	примесямI= за				счет малого	конечного перекрытия=
	волновых функций примесных состояний=EрисK8KOFK=
				æ	b	ö
	Здесь= s = sP exp			ç -	P	÷ I=где сомножитель= sP			очень сильно=
					q
			M	è		ø		M
	зависит от концентрации примесей=kdK=
	Следует		помнитьI=		что необходимым условием прыжка=
	является наличие свободных мест на донорах= Eдва электрона на=
	узле= –	невыгодноFK		=При			низких температурах		это можно =
	обеспечить		только				компенсацией	полупроводникаI= т.еK=

присутствием некоторой части неосновных примесей= EнапримерI= акцепторовFK==

N8M=

=