3. Вычисление работы.

Задача1. Какую работу надо совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки в 1 Н она растягивается на 1 см?

Решение. Работа переменной силы X = f (x) , действующей в направлении оси Ox на отрезке [a,b], вычисляется по формуле

b

A=∫ f (x)dx .

				a
x	Согласно закону Гука, сила X				Н, растягивающая пружину на
	м, равна X =kx .			Коэффициент пропорциональности k найдем
из		условия: если		x =0,01 м,	то X =1 H , следовательно,
k =		1	=100 и X =100x . Тогда
		0,01
		0,04				00,04 =0,08 Дж .
			A= ∫100xdx =50x2
				0

§ 5. Несобственные интегралы

Мы находили определенные интегралы на конечном отрезке и от непрерывной функции. Если одно из этих условий нарушается, то говорить об определенном интеграле уже нельзя. Такие интегралы называются несобственными. Несобственные интегралы бывают двух видов.

1. Интегралы с бесконечными пределами.

Пусть функция f (x) непрерывна на промежутке [a,+∞). Ин-

+∞

теграл ∫ f (x)dx называется несобственным интегралом первого

a

рода. По определению считаем, что

1 Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах: учеб. пособие для вузов: в 2 ч. 5-е изд., испр. Ч. 1.

М.: Высш. шк., 1996. С. 262.

— 152 —

+∞		b
∫ f (x)dx = lim		∫ f (x)dx .
a	b→+∞	a

Если этот предел существует и конечен, то говорят, что интеграл сходится; если предел равен бесконечности или не существует, то говорят, что интеграл расходится.

b +∞

Аналогично определяются интегралы ∫ f (x)dx и ∫ f (x)dx .

−∞ −∞

Пример 1. Найти площадь фигу-

	ры, ограниченной линиями y =	1	,
		x
	y =0 и x =1 .

Решение. Речь здесь идет о площади неограниченной фигуры (на рисунке график изображен пунктиром). Очевидно, искомая площадь может быть найдена с помощью несобствен-

+∞ 1

ного интеграла ∫1 x dx . Имеем

+∞	1		b	dx
∫		dx = lim	∫		= lim ln x		1+∞ =+∞.
	x			x
1		b→+∞	1		b→+∞

Предел равен бесконечности, интеграл расходится и площадь «бесконечна».

Пример 2. Найти площадь фигуры, ограниченной линиями

	y =	1	, y =0 и x =1 .
		x2		1
	Решение. Кривая y =				на рисунке изображена сплошной ли-
				x2

нией. Имеем

— 153 —

+∞ 1				b	dx			1		+∞
∫			dx = lim	∫			= lim −			=−0+1=1.
	x	2			x	2		x
1			b→+∞	1			b→+∞			1

Получен удивительный результат: площадь неограниченной фигуры оказалась конечной!

2. Интегралы от неограниченных функций.

Пусть функция f (x) имеет бесконечный разрыв во внутренней точке c отрезка [a,b] и непрерывна во всех остальных точках отрезка. Считаем по определению

b c−ε b

∫ f (x)dx =lim ∫ f (x)dx+lim ∫ f (x)dx .
a	ε→0	a	δ→0	c+δ

Этот интеграл называется несобственным интегралом второго рода. Если оба предела в правой части равенства конечны, то интеграл сходится, в противном случае — расходится.

3

dx

Пример.

Вычислить несобственный интеграл ∫

или до-

x−2

1

казать его расходимость.

Решение.

Функция

1

непрерывна во всех точках отрезка

x−2

[1,3], а в точке x =2 имеет бесконечный разрыв. Имеем:

3

dx

2−ε

dx

3

dx

12−ε +

∫

=lim

∫

+lim ∫

=limln

x−2

x−2

x−2

1

ε→0

1

δ→0 2+δ x−2

ε→0

+lim ln

x−2

3

==lim(ln ε−ln1)+lim(ln1−ln δ)=−∞+∞.

δ→0

2+δ

ε→0

δ→0

Поскольку оба предела равны бесконечности, то интеграл расходится.

— 154 —

ÉãÄÇÄ 4. èйзьнаЦ й газЦвзйе икйЙкДееакйЗДзаа

§ 1. Предварительные замечания

Как известно из средней школы, уравнение прямой на плоскости задается так:

ax+by +c =0 ,

где x и y — переменные, a, b и с — некоторые числа, причем

a и b не равны нулю одновременно. Всякую прямую можно построить по двум ее точкам. Если a ≠0 и b ≠0 , то вначале можно

взять x =0 , тогда y =−bc , затем взять y =0 , тогда x =−ac . Таким

	c			c
образом, получается две точки — 0;−			и −		;0 , через которые
				a
	b

и проходит данная прямая.

Если одно из чисел, a или b , оказывается равным нулю, то получается горизонтальная или вертикальная прямая, построить которую еще легче.

Предположим теперь, что задано неравенство ax+by +c ≤0 .

Какое множество на плоскости задает это неравенство? Очевидно, что точка (x0 ; y0 ) принадлежит данному множеству, если ее

координаты удовлетворяют неравенству. Можно показать, что неравенству удовлетворяют точки полуплоскости, границей которой служит прямая ax+by +c =0 . Пусть, например, требуется постро-

ить полуплоскость, заданную неравенством 2x−3y−6≤0 . Вначале строим граничную прямую через точки (0;−2) и (3;0). Эта

прямая не проходит через начало координат. Для выбора одной из двух полуплоскостей, определяемых этой прямой, подставим координаты начала в исходное неравенство. Получим

— 155 —

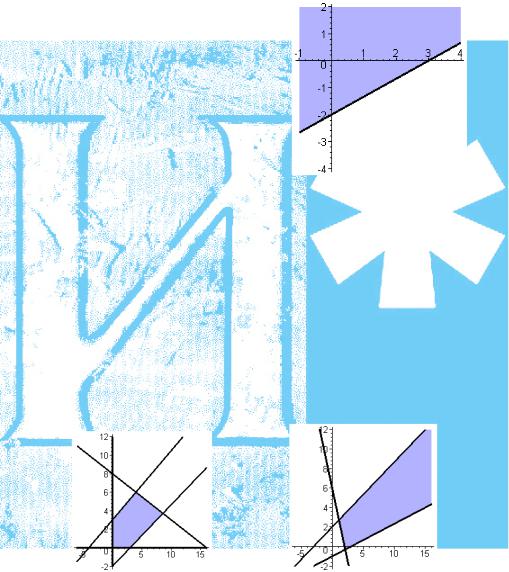
2 0−3 0−6≤0 −6≤0 .

Неравенство верно, поэтому начало координат (точка (0;0)) при-

надлежит искомой полуплоскости. Значит, неравенство задает именно ту полуплоскость, в которой лежит начало координат (см. рис.).

Пусть теперь задано не одно неравенство, а система неравенств. Поскольку каждое неравенство определяет полуплоскость, то система будет определять пересечение полуплоско-

стей. Пересечение полуплоскостей может оказаться ограниченным (тогда мы будем его назвать многоугольником), неограниченным (многоугольная область), или пустым. Рассмотрим пример.

Найти и изобразить на декартовой плоскости множества точек, являющихся решениями следующих систем:

x+2y ≤16
2x−3y ≤6	3x+y ≥6
(а) 3x−4y ≥−12	; (в) 2x−3y ≥−6 .
x ≥0	3x−9 y ≤9
y ≥0

Искомые множества показаны на рисунках.

— 156 —

В первом случае получается многоугольник, т. е. ограниченное множество, во втором — неограниченная область.

Уравнение ax +by +cz +d =0 , где a, b и c не равны нулю од-

новременно, задает плоскость в пространстве R3 . Можно показать, что соответствующее неравенство ax +by +cz +d ≥0 (или

ax+by +cz +d ≤0 ) задает полупространство. Повторяя приведен-

ные выше рассуждения, мы приходим к выводу, что решением системы линейных неравенств с тремя неизвестными может быть либо многогранник, либо многогранная область (неограниченная), либо пустое множество.

Говорят, что уравнение a1x1 +a2 x2 +...+an xn =b задает в про-

странстве Rn гиперплоскость. Решением системы линейных неравенств с n неизвестными будет либо многогранник в n –мерном пространстве, либо многогранная область, либо пустое множество.

Пусть X1, X2 , X3 ,..., Xm — множество точек n –мерного про-

странства. Выпуклой линейной комбинацией этих точек называется точка

m

X =c1 X1 +c2 X2 +...+cm Xm =∑ci Xi ,

i=1

где ci ≥0 и c1 +c2 +...+cm =1 .

Рассмотрим примеры.

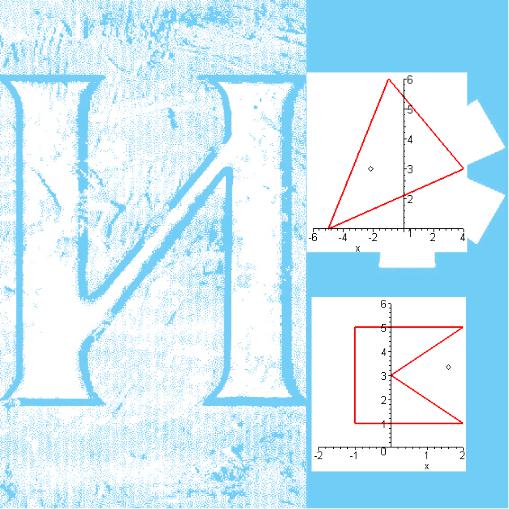
1. Найти выпуклую линейную комби-

1

X1

2

X2 , если X1

и X2 —

нацию

X =

+

3

3

точки

декартовой

плоскости,

причем

X1(1;2)

и X2 (4;−2) .

Решение. По правилам действий с век-

торами

1

2

1

2

X =

X1 +

X

2 =

(1;2)+

(4;−2)=

3

3

3

3

— 157 —

		1		2		8		−4			9		−2			2
	=		;		+		;			=		;			= 3;−		.
		3		3		3		3			3		3			3

Отметим, что полученная точка лежит внутри
																																																						отрезка X1; X2
(см. рис.).
2.										Найти																		выпуклую																			линейную							комбинацию
Y =		1		Y		+				1	Y +						1			Y					, если Y (−1;6) , Y (−5;1)																										и Y (4;3) .
	3															6
					1			2				2											3										1														2						3
Решение. По правилам действий с
векторами
Y =		1		(−1;6)+											1				(−5;1)+													1		(4;3)=
	3																															6
														2
			1										5						1								4			1									13
= −					;2 + −											;							+						;			= −													;3 .
			3										2						2								6			2											6
Эта									линейная																	комбинация																			лежит
внутри треугольника с вершинами в за-
данных точках.
3. Найти выпуклую линейную ком-
бинацию												Z =						1				Z +						1	Z				+				1		Z				+				1	Z		+	1	Z		, если	точки
																											3								12											24					24
																2								1							2										3								4				5
Z1, Z2					, Z3 , Z4 и Z5																					—				вершины																пяти-
угольника												Z1(2;5) ,																Z2 (2;1) ,														Z3 (0;3) ,
Z4 (−1;5) и Z5 (−1;1) .
Решение. По правилам действий с
векторами
	Z =						1		(2;5)+												1			(2;1)+									1				(0;3)+
						2																											12
																			3																												.
					1			(						)									1 (										)				19						10
+				24				−1;5								+							24			−1;1 =																;			3
																																					12

Полученная линейная комбинация не лежит внутри пятиугольника с вершинами в заданных точках.

— 158 —