Значит, вероятность пересечения независимых событий равна произведению их вероятностей.
Пример 4. Вероятность попадания в цель при сбрасывании одной бомбы равна p = 0,1. Найти вероятность попадания в цель хотя бы одной бомбы, если бомбометание производят 10 самолетов, каждый из которых сбрасывает одну бомбу.
Пусть событие B представляет собой попадание хотя бы одной бомбы в цель. Противоположное событие ¬B состоит в непопадании ни одной бомбы в цель. В данном примере попадания в цель разных бомб можно считать независимыми событиями, т. к. каждый самолет действует независимо от других. На основании выведенной формулы вероятность того, что ни одна бомба не попадет в цель составляет
P(¬B)=(1− p)10 .
Для определения искомой вероятности P(B) теперь следует использовать соотношение
P(B) = 1 – P(¬B).
Следовательно,
P(B)=1−(1−0,1)10 ≈0,63 .
Непосредственное вычисление этой вероятности весьма сложно.
§ 9. Формула полной вероятности и формула Байеса
Пусть события A1, A2 , ... , An составляют полную группу несо-
вместных событий, вероятности которых известны. Пусть также нас интересует событие B, для которого известны все условные ве-
— 206 —
роятности P(B | Ai ) (i =1,2,3,..., n). Нужно найти вероятность со-
бытия B.
Поскольку события Ai образуют полную группу, то их объеди-
нение — достоверное событие. Событие B может появиться только с одним из Ai , т. к. события Ai несовместны. Но в этом случае и
события BA1, BA2 , ... , BAn также несовместны, и можно применить аксиому сложения
Значит, вероятность события B равна сумме вероятностей событий A1, A2 , ... , An , умноженных на соответствующие условные
вероятности события B. Эта формула называется формулой полной вероятности.
Пример. На заводе, изготовляющем гайки, первая машина производит 30%, вторая 45% и третья 25% всех изделий. Брак в их продукции составляет 5, 7 и 4% соответственно. Какова вероятность того, что случайно выбранная гайка окажется дефектной?
Обозначим через A событие, состоящее в том, что случайно выбранная гайка окажется дефектной, а через B1, B2 , B3 — события,
состоящие в том, что эта гайка произведена соответственно первой, второй и третьей машинами. Здесь применима формула полной вероятности. Используя условие задачи, получаем
Пусть теперь нас интересует вопрос, какова вероятность того, что гайка, оказавшаяся дефектной, сделана первой (второй, третьей) машиной. Иначе говоря, надо найти вероятность события B1
(B2 , B3 ) при условии, что произошло событие A.
— 207 —
P(A)
На основании теоремы об умножении вероятностей
P(ABi )=P(A)P(Bi | A)=P(Bi )P(A | Bi ).
Отсюда следует, что
P(Bi | A)= P(Bi )P(A | Bi ).
Подставляя сюда выражение P(A) из формулы полной вероятности, получаем
P(Bi | A)=
P(Bi )P(A | Bi )
.
P(Bi )P(A | B1 )+ ... +P(Bn )P(A | Bn )
Эта формула называется формулой Байеса, и наша задача решается так:
P(B | A)=
0,3 0,05
=
150
≈0,265 .
1
0,0565
565
§ 10. Повторение опытов
Рассмотрим сложный опыт, состоящий из нескольких простых опытов, в каждом из которых может появиться или не появиться некоторое событие A. Предположим, что простые опыты независимы, т. е. вероятность P(A) = p в каждом опыте не зависит от результатов других опытов.
Пусть произведено n опытов. Найдем вероятность того, что событие A произойдет m раз (m≤n). Для этого необходимо, чтобы появилась одна из последовательностей событий B1 , B2 ,..., Bn , в которых m из событий B1 , B2 ,..., Bn , совпадают с A, а n−m — с противоположным событием ¬A. Поскольку в этих последовательностях не учитывается порядок следования Bi , то их число равно числу подмножеств из n элементов по m, т. е. числу
— 208 —
Cm =
n!
.
(n−m)!m!
n
В силу независимости опытов вероятность каждой такой последовательности по теореме умножения для независимых событий
равна pmqn−m , где q = 1 – p. В силу несовместности всех возмож-
ных последовательностей искомая вероятность равна сумме вероятностей всех последовательностей, состоящих из m событий A и
n−m событий ¬A, т. е. сумме Cnm слагаемых, равных pmqn−m :
P
=Cm pmqn−m =
n!
pmqn−m .
(1)
m,n
n
m!(n−m)!
Введем вспомогательную переменную u и отметим, что величина
Pm,num =Cnm pmqn−mum
представляет собой общий член разложения функции (q+ pu)n по формуле бинома Ньютона. Значит, вероятность Pm,n является коэффициентом при um в разложении функции
ϕn (u)=(q + pu)n
(2)
по степеням u.
Функция ϕn (u) называется производящей функцией для вероятностей Pm,n . Элементарными событиями в данном случае служат
все конечные последовательности {B1, B2 ,..., Bn }, где каждое Bi
представляет собой событие A или противоположное событие ¬A. Полем событий T служит алгебра всех возможных объединений этих элементарных событий, дополненная невозможным событием.
Вероятность каждого элементарного события равна pmqn−m , где
m— число событий Bi в последовательности {B1, B2 ,..., Bn }, сов-
—209 —
падающих с A. Вероятность любого события определяется сумма вероятностей входящих в него элементарных событий. ответствие между числами m = 0, 1, ..., n и вероятностями Pm,n
как Сона-
зывается биномиальным распределением.
Формулы (1) и (2) можно обобщить на случай, когда вероятность события A имеет различные значения в разных опытах. Если эти опыты независимы и вероятность события A в k-м опыте равна
pk , qk =1− pk (k =1,2,...,n), то вместо (1) аналогичным способом получается формула
Pm,n =∑pi1 ...pim qim+1 ...qin ,
(3)
где сумма распространена на все возможные разделения чисел 1, 2, ..., n на две группы, одна из которых содержит m чисел
(i1,i2 , ... ,im ), а другая n−m чисел (im+1,im+2 , ... ,in ). Число таких разделений равно Cnm .
В этом случае вероятность Pm,n представляет собой коэффициент при um в разложении по степеням u производящей функции
n
ϕn (u)=∏(qi + piu).
1
Во многих практических задачах приходится определять вероятность того, что интересующее нас событие A появится при n
опытах не менее чем k раз (k ≤n).
Сложное событие — появление события A не менее k раз — представляет собой объединение n – k + 1 несовместных событий: появление A ровно k раз, появление A ровно k + 1 раз и т. д., появление A ровно n раз. Значит, искомая вероятность Rk,n того, что
при n опытах событие A появится не менее k раз, равна
n
Rk ,n =Pk ,n +Pk+1,n + ... +Pn,n =∑Pi,n . i=k
— 210 —
Эту вероятность также можно вычислить, определив сначала вероятность противоположного события, т. е. вероятность того, что событие A появится меньше чем k раз, и вычтя ее из единицы:
k−1
Rk ,n =1−P0,n −P1,n − ... - Pk -1,n =1−∑Pi,n . 0
Чаще всего приходится вычислять вероятность того, что некое событие появится хотя бы один раз. Очевидно, что здесь при любом n ≥2 лучше пользоваться предыдущей формулой, т. к. сумма в ней
содержит только одно слагаемое P0,n . В результате получим
R1,n =1−P0,n =1−q1q2...qn .
(4)
В частном случае постоянных условий опыта q1 =q2 = ... =q и формула (4) принимает вид
R1,n =1−qn .
êЦбыеЦ
В разделе представлены начальные понятия теории вероятности, знакомство с которыми является необходимым для студентов гуманитарных направлений.
Çйикйлх Сгь лДейикйЗЦкда
1.Что больше, A53 , или C53 ?
2.Что такое элементарное событие?
3.Приведите пример совместных событий и несовместных событий.
4.Что значит «зависимые события» и «независимые события»?
5.Каким условиям должна удовлетворять группа событий, чтобы к ней можно было применить формулу полной вероятности?
—211 —
бДдгыуЦзаЦ
Одной из основных целей курса математики для гуманитариев является развитие мышления. Известно, что математика воспитывает такой склад ума, который всегда требует критического отношения и логического обоснования любого взгляда на то, или иное явление. Поэтому считается, что главным в курсе математики должно быть не конкретное изучение основ науки как таковой, а общеинтеллектуальное развитие. Однако если заглянуть в Государственный образовательный стандарт высшего профессионального образования (для гуманитарных направлений), то мы увидим там как раз конкретные разделы математики. В данном пособии мы предлагаем студентам познакомиться с наиболее важными (на наш взгляд) из этих разделов. Таковыми являются: основы теории множеств, основы математической логики, основы теории отношений, матрицы и операции над ними и основы теории вероятностей. Каждый из названных разделов, помимо указанной выше цели развития мышления, вполне может потребоваться в профессиональной деятельности выпускника гуманитарного направления.
— 212 —
икДднадме
РАЗДЕЛ I
1. Элементы теории множеств
Задача 1. Даны два числовых множества
A={1, 3, 5, 7} и B ={−2, 0, 3, 5}.
Найти: 1) A B; 2) A∩B; 3) A−B; 4) B−A; 5) A ∆ B.
Решение.
1) По определению объединения множеств, в него должны входить элементы из A, элементы из B, а также общие для A и B эле-
менты. Поэтому A B ={−2, 0, 1, 3, 5, 7}.
2) По определению пересечения множеств, оно содержит только общие для рассматриваемых множеств элементы. Поэтому
A∩B ={3, 5}.
3) По определению, разность двух множеств состоит только из тех элементов первого множества, которые не принадлежат второму. Поэтому, чтобы найти разность A и B, нужно удалить из A об-
щие для A и B элементы, т. е. A−B ={1, 7}.
4)Аналогично получаем B−A={−2, 0}.
5)Симметрическая разность двух множеств A и B — это объединение разностей A−B и B−A , поэтому A ∆ B ={−2, 0, 1, 7}.
Задача 2. Задать с помощью характеристического свойства: а) множество всех натуральных чисел, меньших 10; б) множество всех нечетных чисел;
в) множество всех чисел, больших –1 и меньших либо равных 5.
Решение.
Используя правило записи множества через характеристическое свойство, а также элементарные математические символы, изучаемые в младших классах, получаем:
а) {x N : x <10} (читается так: множество натуральных чисел икс, таких, что икс меньше десяти);
— 213 —
б) {x : x =2n−1, n N} (множество таких иксов, что икс равен два эн минус единица, где эн — натуральное число);
в) {x R : −1<x ≤5} (множество действительных чисел икс,
таких, что икс больше минус единицы и меньше либо равен пяти). Разумеется, после минимальной тренировки уже не потребуется предварительно проговаривать символическую запись на русском
языке (или на любом другом).
Задача 3. Задать следующие множества способом перечисления их элементов:
а) M ={x N : x <6};
б) M ={x Z : −4<x <2}.
Решение.
а) Это множество натуральных чисел, меньших 6, поэтому
M ={1, 2, 3, 4, 5}.
б) Это множество целых чисел, больших –4 и меньших 2, по-
этому M ={−3, −2, −1, 0, 1}.
Задача 4. Определить отношения между множествами:
а) N, R, Z и Q;
б) прямоугольников и параллелограммов; в) студентов ТюмГУ и студентов факультета ГМУ.
Решение.
а) Здесь даны множества N (натуральных чисел), R (действительных чисел), Z (целых чисел) и Q (рациональных чисел). Всякое натуральное число является целым, но не наоборот; всякое целое число является рациональным, но не наоборот; всякое рациональ-
ное число (т. е. всякая дробь вида mn , где n — натуральное, а m —
целое) является действительным, но не наоборот (например, 2 — действительное число, но не рациональное, т. к. его нельзя запи-
сать в виде дроби mn ). Поэтому ясно, что эти множества удовле-
творяют соотношению
— 214 —
N Z Q R .
б) Как известно из курса геометрии 7 класса, всякий прямоугольник — параллелограмм, но не всякий параллелограмм — прямоугольник, поэтому множество прямоугольников есть часть (подмножество) множества параллелограммов.
в) Очевидно, множество студентов факультета ГМУ является частью множества студентов ТюмГУ.
Задача 5. Пусть R — универсальное множество. Найти дополнения (до универсального) следующих множеств:
а) M1 =(−∞; 3];
б) M2 ={x R : −4≤x<2};
в) Q.
Решение.
Дополнение данного множества до универсального — это разность между универсальным и данным множествами, поэтому получаем:
а) ¬M1 =R−M1 =(3; +∞);
б) ¬M 2 =R−M 2 =(−∞; −4) [2; +∞);
в) ¬Q =R−Q , т. е. множество иррациональных чисел.
Задача 6. Пусть универсальное множество U — множество сотрудников некой организации; A — множество всех сотрудников данной организации старше 45 лет; B — множество сотрудников, имеющих стаж работы в данной организации менее 5 лет; C — множество начальников.
Описать словами (указать характеристическое свойство) следующие множества:
1) ¬C;
2) C −A;
3) A∩(C −B).
Решение.
1) Поскольку дополнение множества — это разность между универсальным и данным множествами, то ¬C — множество сотрудников, не являющихся начальниками.
2) C −A — это начальники, но не старше 45 лет (перспективные кадры!).
— 215 —
3) A∩(C −B) — начальники старше 45 лет, имеющие стаж ра-
боты в данной организации не менее 5 лет (неперспективные). Задача 7. Изобразить с помощью диаграммы Венна следующие
множества:
1) ¬A−B;
2) A∩B ∩C.
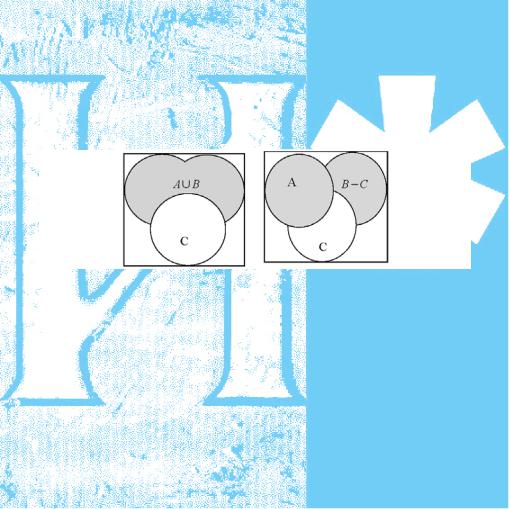
Решение. В данном случае следует рисовать круги, изображающие множества на диаграмме, в стандартной позиции.
1)На рис. 1 искомое множество изображено более темным цве-
том.
2)На рис. 2 центральная область является пересечением трех заданных множеств.
Задача 8. Проиллюстрировать с помощью диаграмм справедливость равенства
(A B)−B =A−B .
Решение. Чтобы показать справедливость этого соотношения, мы должны нарисовать две диаграммы: первая для левой части равенства, вторая — для правой. Если в результате получатся одинаковые результирующие множества, то соотношение верно.
Легко видеть, что именно так и будет. В первом случае вначале A и B объединяются, а затем из объединения выбрасывается B —
— 216 —
остается серп A. Во втором случае из круга A удаляется часть, принадлежащая B — остается вновь серп A.
Задача 9. Определить, в каком случае выполняется соотноше-
ние A B = A∩B.
Решение. Объединение двух множеств, это гантель, а пересечение их — лунка. В общем случае, лунка является частью гантели ( (A∩B) (A B) ). Чтобы они совпали, очевидно, требуется, что-
бы совпали круги A и B. Таким образом, должно быть A=B . Задача 10. Верно ли равенство
Результат операций для левой и правой частей формулы обозначен темным цветом. Очевидно, что равенство неверно.
2. Элементы математической логики
Задача 1. В следующих сложных высказываниях обозначить буквами элементарные составляющие и определить, какие из сложных высказываний имеют одинаковую структуру:
а) если одно из слагаемых делится на 3 и сумма делится на 3, то и второе слагаемое делится на 3;
б) если одно слагаемое делится на 3 и второе слагаемое не делится на 3, то сумма не делится на 3;
в) если число рациональное или иррациональное, то оно вещественное;
г) если a =0 или b =0 , то ab =0 ;
— 217 —
д) если число не является вещественным, то оно не является рациональным и не является иррациональным;
е) если ab ≠0 , то a ≠0 и b ≠0 ; ж) если a ≠0 и b ≠0 , то ab ≠0 .
Решение. Обозначим в высказывании (а): p — «одно из слагаемых делится на 3», q — «сумма делится на 3», r — «второе слагаемое делится на 3». Тогда получится формализованная запись p q r .
В высказывании (б) обозначим: p — «одно слагаемое делится на 3», q — «второе слагаемое делится на 3», r — «сумма делится на 3». Получается — p¬q ¬r .
Для остальных высказываний имеем: (в) p q r ;
(г) p q r ;
(д) ¬p ¬q¬r ; (е) ¬p ¬q¬r ; (ж) ¬p¬q ¬r .
Можно выделить следующие группы высказываний, имеющих одинаковую структуру:
1группа — (а);
2группа — (б);
3группа — (в) и (г);
4группа — (д) и (е);
5группа — (ж).
Задача 2. Найти значения следующих сложных высказываний, если известно, что p = Л, q = И, r = И:
а) p (q r) ;
б) p q¬r ;
в) p ∆ (q r) ;
г) p q ¬q r .
Решение. Чтобы ответить на вопросы задачи, надо использовать определения логических операций, учитывая порядок действий.
а) Вначале выполняется операция в скобках q r . По опреде-
лению, конъюнкция двух простых высказываний истинна только в том случае, когда истинны обе ее составляющие. В нашем случае
— 218 —
q =И , r =И , поэтому q r =И . Так как p =Л , то конъюнкция
Л И = Л . Значение первой формулы — ложь.
б) Подставим логические значения в формулу, получим Л И¬И . Согласно порядку действий, вначале выполняется отрицание, затем конъюнкция и, наконец, импликация. Найдем логическое значение этого высказывания.
Л И¬И ≡ Л И Л ≡ Л Л ≡И .
Таким образом, значение высказывания (б) — истина.
в) Подставляем логические значения переменных в формулу Л ∆ (И И) . Выполним указанные действия
Л ∆ (И И) ≡Л ∆ И ≡И . Значение высказывания (в) — истина.
г) Подставим логические значения переменных и преобразуем формулу
Л И ¬И И ≡И Л И ≡И Л ≡Л .
Здесь также получилась ложь.
Задача 3. Известно, что импликация p q истинна, а эквиваленция p q ложна. Что можно сказать о значении импликации q p ?
Решение. По определению, импликация двух высказываний истинна в трех вариантах сочетания значений ее составляющих:
И— И, Л — И, Л — Л. Эквиваленция двух простых высказываний ложна в двух вариантах сочетания значений ее составляющих:
И— Л и Л — И. Поскольку «простые высказывания» в этих формулах одни и те же (p и q), то остается выбрать общий вариант сочетания логических значений, это будет Л — И. Тогда импликация q p ≡И Л ложна.
Задача 4. Упростить запись следующих формул:
а) (((p q)¬r) ((q r) (p q)));
б) (p (q (r (¬r q)))).
— 219 —
Решение. Руководствуемся тремя правилами упрощения (см. лекционный курс). Следует убрать лишние скобки, но так, чтобы не нарушать порядок действий, а также опустить знаки конъюнкции. Приведем поэтапное преобразование формулы.
(((p q)¬r) ((q r) (p q)))≡
((p q)¬r) ((q r) (p q))≡
(p q)¬r q r (p q)≡
(p q)¬r q r (p q).
Вформуле (б) можно убрать лишь одни внешние скобки и знак конъюнкции. Получим
p(q (r (¬r q))).
Задача 5. Составить таблицы истинности для формул:
а) ¬p p ∆ q ;
б) pq ¬p q ;
в) p(q r) p¬q .
Решение. В первой формуле содержится две переменные и связывающие их три логические операции, поэтому таблица будет со-
держать 4 строчки ( 22 =4 ) и 5 столбцов (по одному на каждую переменную и на каждую операцию). Таблица заполняется последовательно слева направо и сверху вниз. Вначале заполняются столбцы, соответствующие переменным p и q, затем, согласно определениям логических операций, остальные столбцы. Для большей наглядности будем вместо букв И и Л писать знаки + и −.
p
q
¬p
p ∆ q
¬p p ∆ q
+
+
–
+
+
–
+
+
–
–
+
–
–
+
+
–
–
+
–
–
— 220 —
В последнем столбце этой таблицы получены логические значения формулы (а).
Аналогичным образом заполним таблицу для формулы (б). В ней будет 4 строки и 6 столбцов, т. к. операций уже не три, а четыре.
p
q
pq
¬p
¬p q
pq ¬p q
+
+
+
+
–
+
–
+
–
+
+
+
+
–
–
–
–
+
–
–
–
+
+
+
Заметим, что все значения в правом столбце — истина, значит, формула (б) тождественно истинная.
В третьей таблице будет уже 8 строк (т. к. переменных — три) и 8 столбцов.
p
q
r
q r
p (q r)
¬q
p¬q
p (q r) p¬q
–
+
+
+
+
+
–
–
–
+
+
+
–
–
–
+
+
–
+
+
+
+
+
+
+
+
–
+
+
–
–
–
+
–
–
–
–
+
+
–
–
+
–
+
–
–
–
+
–
–
+
+
–
+
–
+
–
–
–
–
–
+
–
+
Задача 6. Доказать равносильность путем преобразований на основании законов логики высказываний:
а) p (q r)≡ pq r ;
б) pq p¬q¬pq¬p¬q ≡È .
Решение. Проведем тождественные преобразования в виде цепочки действий (см. лекции), причем левые части формул приведем к правым.
— 221 —
Формула (а):
p (q r)≡ p ¬q r(18) ≡
¬p ¬q r(18)≡¬(pq) r(16)≡ pq r(18) .
Что и требовалось доказать. Формула (б):
pq p¬q ¬pq ¬p¬q ≡ p(q ¬q) ¬p(q ¬q)(6)
≡ pÈ ¬pÈ(10)≡È (p ¬p)(2,6)≡ÈÈ(10)≡È(8) .
Что и требовалось.
Задача 7. Используя законы де Моргана, преобразовать следующие формулы так, чтобы знак отрицания был отнесен к отдельным переменным:
а) ¬(¬p q);
б) ¬(pq ¬r);
в) ¬(p(q ¬r)).
Решение. Имеем
а) ¬(¬p q)≡ p¬q ;
б) ¬(pq ¬r)≡¬(pq)r ≡(¬p ¬q)r ;
в) ¬(p(q ¬r))≡¬p ¬(q ¬r)≡¬p ¬qr .
Задача 8. Дать обоснованные ответы на вопрос: следует ли из посылок заключение?
Посылки
Заключение
1.
Если число оканчивается нулем, то оно
делится на 5
Число делится на 5
2.
Число оканчивается нулем
1.
Если число оканчивается нулем, то оно
делится на 5
Число не делится на 5
2.
Число не оканчивается нулем
1.
Если число оканчивается нулем, то оно
Число оканчивается ну-
делится на 5
лем
2.
Число делится на 5
— 222 —
Посылки
1.Если число оканчивается нулем, то оно делится на 5
2.Число не делится на 5
1.Если число целое, то оно рациональное
2.Если число — несократимая дробь, то оно не целое
1.Если число — дробь, то оно рациональное
2.Если число целое, то оно рациональное
1.Если посылки истинны и рассуждение правильное, то и заключение истинно
2.Заключение ложно
Заключение
Число не оканчивается нулем
Если число — несократимая дробь, то оно не рациональное
Если число целое, то оно дробь
Посылки ложны или рассуждение неправильное
Решение. Формализуем данные логические следования.
а) Пусть p — «число оканчивается нулем», q — «число делится на 5». Тогда логическое следование имеет вид
p q, p . q
Структура логического следования совпадает с правилом заключения, значит, логическое следование верно.
б) Используя предыдущие обозначения, имеем
p q,¬p .
¬q
Структура логического следования не совпадает ни с одним из приведенных в курсе лекций правил вывода, поэтому для доказательства его правильности можно, например, составить таблицу
истинности для формулы (p q)¬p ¬q .
p
q
p q
¬p
(p q)¬p
¬q
(p q)¬p ¬q
+
+
+
–
–
–
+
–
+
+
+
+
–
–
+
–
–
–
–
+
+
–
–
+
+
+
+
+
— 223 —
Поскольку формула не является тождественно истинной, то логическое следование неверно.
в) Структура логического следования имеет вид p q, q
p
и не совпадает ни с одним из правил вывода. Для доказательства можно вновь составить таблицу истинности формулы
(p q)q p . Эта формула не тождественно истинна, значит, ло-
гическое следование неверно.
г) Структура логического следования имеет вид
pq,¬q ¬p
исовпадает с правилом отрицания. Значит, логическое следование имеет место.
д) Структура логического следования имеет в данном случае
вид
p q,r ¬p
r¬q
ине совпадает ни с одним из правил вывода. Соответствующая логическая формула тождественно истинной не является, следовательно, правило неверно.
е) Структура логического следования имеет вид
p q, r q
r p
и не совпадает ни с одним из правил вывода. Формула также не тождественно истинна, значит, следование не имеет места.
ж) Структура логического следования имеет вид pq r,¬r
¬p¬q
— 224 —
и не совпадает ни
с одним из правил
вывода. Формула
(pq r)¬r ¬p¬q
тождественно истинна,
поэтому логическое
следование верно.
Задача 9. Записать логической формулой следующее сложное высказывание (эта задача взята из книги Г. И. Москиновой1 ):
«Если фирма приглашает на работу крупного специалиста в области новых технологий, то она считает их привлекательными и разворачивает работы по изменению технологии производства своего традиционного продукта или начинает разработку нового продукта. Конкурирующая фирма пригласила на работу крупного специалиста в области новых технологий. Следовательно, она разворачивает работы по изменению технологии производства выпускаемого продукта или разработке нового продукта».
Уточнить справедливость данного высказывания. Решение. Введем обозначения простых высказываний:
p — фирма продолжает выпуск существующего продукта; q — фирма ориентирована на существующий рынок;
r — фирма разворачивает работу по изменению технологии производства своего традиционного продукта;
s — фирма начинает разработку нового продукта.
С учетом принятых обозначений высказывание примет вид
p q(r s), p . r s
Эта схема похожа на правило заключения. Формально отличие заключается только в том, что заключение не содержит q. Однако
конъюнкция q(r s) истинна только тогда, когда истинны оба высказывания q и r s . Истинность q следует из контекста, стало быть, истинна и дизъюнкция r s . Таким образом, данное высказывание истинно при истинности q.
1 Москинова Г. И. Дискретная математика. Математика для менеджера в примерах и упражнениях: учеб. пособие. М.: Логос, 2000. 240 с.
— 225 —
Задача 10. Доказать логическое следование:
а) (p q r,¬p¬q) r ; б) (p q r,¬p) q r .
Решение. Применим правило доказательства логического следования. Для этого составим таблицу, в первом столбце которой будем записывать либо посылку, либо следствие из посылок на основании законов логики высказываний или правил вывода.
а)
p q r
посылка
(p q) r
закон 5 (из 1)
¬p¬q
посылка
¬(p q)
закон 17 (из 3)
r
УД (2; 4)
В последней строчке таблицы получена правая часть формулы. На этом доказательство считается законченным.
б)
p q r
посылка
p (q r)
закон 5 (из 1)
¬p
посылка
q r
УД (2; 3)
Что и требовалось.
Задача 11. Записать область истинности предиката P(x): «x — простое число», определенного на множестве
M ={1,2,3,4,5,6,7,8,9}.
Решение. Простым называется натуральное число, делящееся (нацело) только на единицу и на себя. Таким образом, область истинности предиката P(x):
D(P)={2,3,5,7}.
— 226 —
Задача 12. Бинарное отношение (двуместный предикат) P(x,y): «x делит y» определено на множестве M 2 , где M ={1,2,3,4,5,6}.
Составить прямоугольную таблицу, задающую этот предикат и определить его область истинности.
1
2
3
4
5
6
1
+
+
+
+
+
+
2
–
+
–
+
–
+
3
–
–
+
–
–
+
4
–
–
–
+
–
–
5
–
–
–
–
+
–
6
–
–
–
–
–
+
Решение. Составим таблицу, в которой x расположен в строчках, а y — в столбцах. Знак «+» обозначает истину, знак «–» — ложь.
Область истинности этого предиката есть множество
,(1,6),(2,2),
(1,1),(1,2),(1,3),(1,4),(1,5)
D(P)=
4),(2,6),(3,3),(3,6),(4,
.
(2,
4),(5,5),(6,6)
Задача 13. Изобразить на диаграммах области истинности следующих предикатов:
а) A(x) B(x) ; (б) A(x) B(x) ; в) ¬A(x) B(x) .
Решение. Используем понятия теории множеств для интерпретации условия данной задачи. Поскольку конъюнкция истинна, когда истинны все ее составляющие, то требуется показать на диаграмме общую область множеств A и B. Это соответствует понятию пересечения. Значит, область истинности предиката A(x) B(x)
можно изобразить как пересечение множеств A и B на диаграмме Венна.
Вторая область истинности определяется из смысла истинностного значения импликации. Импликация ложна только в том случае, когда истинна посылка и ложно заключение. В нашей интер-
— 227 —
претации точка прямоугольника не должна находиться в круге A и, одновременно, не в круге B, т. е. область истинности предиката A(x) B(x) — часть прямоугольника, кроме серпа A.
В силу истинностного значения эквиваленции, левая и правая части третьего соотношения должны иметь одинаковые логические значения. Отсюда следует, что либо одновременно A(x) — истинно, B(x) — ложно, либо, наоборот, A(x) — ложно, B(x) — истинно. Значит, область истинности предиката ¬A(x) B(x) — объединение
двух серпов A и B.
На рисунках показаны области истинности предикатов для случаев (а) и (б).
Задача 14. Предикаты A(x) и B(x) определены на некотором множестве M. В каком отношении должны находиться области истинности A и B этих предикатов, чтобы:
а) A(x) B(x) принимал значение И:
1)для некоторых x из M;
2)для всех x из A;
3)для всех x из B;
4)ни для одного x из M.
б) A(x) B(x) принимал значение И:
1)для всех x из M;
2)ни для одного x из M.
Решение.
а) Предикат A(x) B(x) принимает значение И на пересечении
областей истинности предикатов A(x) и B(x), поэтому:
— 228 —
•для первого случая нужно, чтобы пересечение областей истинности предикатов A(x) и B(x) было непусто, но и не совпадало со всем M (это значит, что круги A и B пересекаются либо в лунке, либо A входит в B ( A≠M ), либо B входит в A ( B ≠M ));
•для второго случая нужно, чтобы область истинности B(x) совпадала с пересечением A(x)∩B(x) , т. е. круг B входит в круг A;
•для третьего случая необходимо, чтобы области истинности предикатов A(x) и B(x) имели пустое пересечение, т. е. круги A и B не имеют общих точек.
б) Область истинности предиката A(x) B(x) — часть прямо-
угольника, за исключением серпа A, поэтому:
•для первого случая — область истинности A(x) должна быть пустой;
•для второго случая — область истинности A(x) совпадает с M, а область истинности B(x) — пустая.
Задача 15. Записать предикатной формулой высказывание «У любого человека есть мать».
Решение. Используем два предиката «P(x): x — человек» и «Q(x, y): y — мать x». Тогда высказывание запишется с помощью кванторов общности и существования
(P(x)) (Q(x, y)) .
Задача 16. Пусть R(x, y) предикат порядка « x≥ y », определенный на множестве
M ={0,1,2,3,4,5,6,7,8,9}.
Рассмотреть различные варианты навешивания кванторов на переменные этого предиката. Определить истинность полученных выражений.
Решение. Существует 8 вариантов навешивания кванторов на переменные. Рассмотрим последовательно каждый из них.
1) ( x)( y)R(x, y) — «для всякого x и всякого y имеет место
R(x,y)», или, иначе, «любое число из M больше или равно любого числа из M». Легко видеть, что это выражение ложно.
— 229 —
2) ( y)( x)R(x, y) . Это высказывание отличается от преды-
дущего только порядком следования одноименных кванторов, поэтому имеет тот же смысл и то же истинностное значение.
3)( x)( y)R(x, y) — «для любого x существует y такой, что
x≥ y », или, иначе, «всякое число из M больше либо равно некоторого числа из M». Это выражение истинно.
4)( y)( x)R(x, y) — «существует y такой, что для любого x
xбольше либо равен y», или, иначе, «существует такое число в M, что все остальные числа из M больше либо равны ему». Это высказывание истинно.
5) ( x)( y)[x ≥ y] — «существует x такой, что для всякого y x≥ y » или «существует в M число, которое больше или равно всех остальных чисел из M». Это высказывание, очевидно, истинно.
6) ( y)( x)[x ≥ y] — «для всякого y существует x такой, что x≥ y », или, иначе, «для всякого числа из M существует число из
M, большее либо равное первому». Это высказывание также истинно.
7) ( x)( y)[x ≥ y] — «существует такой x, что найдется y, ко-
торый меньше либо равен x», или, иначе, «найдутся такие два числа x и y из M, что одно из них (x) больше либо равно другому». Это высказывание верно.
8) ( y)( x)[x ≥ y]. Это высказывание отличается от предыду-
щего только порядком следования одноименных кванторов, поэтому имеет тот же смысл и то же истинностное значение.
3. Матрицы
Задача 1. Найти матрицы 3A+2B и 2A−3B , если
1
2 3
0
−1 2
A=
, B =
.
0
−1 2
1
1 3
Решение. Прежде всего, убеждаемся, что матрицы A и B имеют одинаковые размеры 2×3 .
— 230 —
Согласно определению умножения матрицы на число, имеем
1
2
3 3
6
9
3A=3
=
и
0
−1 2 0
−3 6
0
−1
2 0
−2 4
2B =2
1
=
2
.
1
3 2
6
Далее, находим сумму
3 6 9 0 −2 4 3 4 13
3A+2B =
+
=
.
0 −3 6 2 2 6 2 −1 12
Аналогично
2A−3B =2A+(−3)B =
1 2
3
0 −1 2
=2
+
(−3)
=
0 −1 2
1 1 3
2 2 3
0 3
−6
2
7
0
=
+
=
−5
.
0
−1 2 −3 −3
−9 −3
−5
Задача 2. Найти A и A′, если
1
2
A=
.
−3
4
Решение. Найдем транспонированную матрицу для A, т. е. поменяем в A местами строки и столбцы
1 −3 A′= .
2 4
Поскольку A квадратная матрица, то A′ также квадратная матрица и того же порядка, поэтому можно найти сумму A+ A′. Имеем
1 2 1
−3
2 −1
A+A′=
+
4
=
.
−3 4 2
−1 8
— 231 —
Задача3. Найти произведения AA′ и A′A для матрициз задачи 2.
Решение. Матрицы A и
A′
квадратные (2-го порядка), значит,
согласованы. Произведения AA′ и A′A найти можно.
1
2 1 −3
AA′=
4
=
−3 4 2
1 1+2 2
1 (−3)+2 4
5 5
=
=
.
(−3) 1+4 2 (−3) (−3)+4 4 5 25
1
−3 1
2
A′A=
=
2
4 −3
4
1 1+(−3) (−3) 1 2+(−3) 4 10
−10
=
2 2+4 4
=
.
2 1+4 (−3)
−10 20
Задача 4. Не находя произведения
C = AB и
D =BA , выяс-
нить, будут ли иметь одинаковые размеры матрицы C и D, если
1
A=(2 3 4), B = -2 .
3
Решение. Матрицы A и B согласованы, т. к. количество столбцов матрицы A равно количеству строк матрицы B (равно 3). В результате умножения согласованных матриц получается матрица, у которой количество строк равно количеству строк первой матрицы, а количество столбцов равно количеству столбцов второй матрицы. Таким образом, AB будет иметь одну строку и один столбец (число!).
Матрицы B и A также согласованы, в результате их перемножения получится квадратная матрица 3-го порядка.
Ответ. Матрицы C и D имеют разные размеры.
— 232 —
Задача 5. Найти C = AB и D =BA по условию предыдущей задачи.
Решение. Имеем
1
C =(2 3 4) −2 =(2 1+3 (−2)+4 3)=8,3
1
D = −2 (2 3 4)=3
1 2
1 3
1 4
2
3
4
−6
= (−2) 2 (−2) 3 (−2) 4 = −4
−8 .
3 2
3 3
3 4
6
9
12
Задача 6. Найти A2 и A3 по условию задачи 3.
Решение.
A2 = A A
1
2 1
2
=
=
−3
4 −3 4
1 1+2 (−3)
1 2
+2 4
−5 10
=
=
,
(−3) 1+4 (−3)
(−3) 2+4 4 −15
10
−5
10
1
2
A3 = A2 A =
=
−15
10 −3
4
(−5) 1+10 (−3) (−5) 2+10 4 −35 30
= = .
(−15) 1+10 (−3) (−15) 2+10 4 −45 10
Задача 7. Найти определители матриц A, A2 и A3 из предыдущей задачи.
— 233 —
Решение. Используем правило вычисления определителя второго порядка.
A
=
1
2
=1 4−2 (−3) =4+6=10,
−3
4
A2
=
−5
10
=(−5) 10−10 (−15) =
−15
10
=−50+150=100,
3
−35
30
A
=
−45
10
=(−35) 10−30 (−45) =
=−350+1350 =1000.
Заметим, что
A2
=
A
2 и
A3
=
A
3 .
Задача
8.
Найти
определители матриц A и A′, если
1
0
2
A= −1 2
3 .
4
0
1
Решение. Воспользуемся правилом вычисления определителя 3-го порядка.
Конечно, A = A′ , т. к. определитель квадратной матрицы не
изменяется при ее транспонировании.
Задача 9. Найти определитель четвертого порядка,
2
1
−1
3
4
0
2
−1
,
−3
2
1
1
0
1
1
1
разложив его по элементам какой-либо строки или столбца. Решение. Заметим, что во втором столбце есть нулевой эле-
мент, а также элементы, равные 1. Значит, разложить определитель выгодно по элементам именно этого столбца. Как известно, определитель не изменится, если ко всем элементам некоторой строки прибавить соответствующие элементы любой другой строки, умноженные на любое число. Умножим первую строку на –2 и прибавим к третьей, затем умножим первую строку на –1 и прибавим к последней. В результате во втором столбце определителя будут находиться все нули, а первый элемент — единица, т. е.
2
1
−1
3
2
1
−1
3
4
0
2
−1
=
4
0
2
−1
.
−3 2
1
1
−7
0
3
−5
0
1
1
1
−2
0
2
−2
Теперь разложение определителя по элементам второго столбца осуществляется особенно просто:
2
1
−1
3
4
2
−1
4
0
2
−1
=1 (−1)1+2
−7
3
−5
=
−7
0
3
−5
−2
0
2
−2
−2
2
−2
— 235 —
=−(−24+20+14−6+40−28) =−16.
Задача 10. Найти обратную матрицу для
3
5
A=
.
2
4
Решение. Вначале проверим, обратима ли матрица A, для чего вычислим ее определитель. Поскольку
A
=
3
5
=12−10=2≠0 ,
2
4
то матрица обратима. Используем первый способ нахождения обратной матрицы (через присоединенную), т. к. в нашем случае легко отыскать алгебраические дополнения элементов.
Транспонированная матрица
3
2
Находим матрицу ал-
A′=
.
5
4
гебраических дополнений (присоединенную).
A
Aji
4
−5
=
=
.
−2
3
А
=2 , получаем
Разделив все элементы последней матрицы на
обратную матрицу
5
2
−
2
A−1 =
.
3
−1
Проверка.
2
5
2
−
1 0
−1
2
3 5
A A
=
=
=E ,
2
4
3
0
1
−1
2
таким образом, вычисления правильны.
— 236 —
Задача 11. Найти обратную матрицу двумя способами:
2 способ. Метод Жордана–Гаусса подробно изложен в курсе лекций. Приведенные здесь матрицы служат для контроля правильности вычислений.
1
1
2
−3
0
0
2 4
−6 1
0
0
2
1
1 0
−1 0
1
0 → 0 −2
2
−
1
0 →
2
0 2
−3 0
0
1
2
−3
0
0
0
1
— 237 —
1
0
0
1
0 −1
1 0
−1 0
1 0
2
1
1
3
3
→
0 1
−1
−
0
→
0
1
0
−
−1 →
4
2
4
2
1
1
0 0
1 1
−1 −
0
0
1
−1
−1
2
2
Обратная матрица, конечно же, получилась та же самая.
4. Отношения
Задача 1. Выписать все элементы декартова произведения M ={2, 4} {1, 2, 3}. Каковы здесь область определения и множе-
ство значений?
Решение. По определению, декартово произведение двух множеств — это множество всех упорядоченных пар элементов, таких, что первый элемент пары принадлежит первому множеству, а второй элемент — второму множеству. Таким образом, получаем
M ={(2;1),(2, 2),(2,3),(4,1),(4, 2),(4,3)}.
Область определения здесь {2, 4}, а множество значений
{1, 2, 3}.
Задача 2. Найти область определения и множество значений следующих отношений:
а) M ={(x; y) 2 : x2 = y2 }; б) T ={(x; y) 2 : y >x2 }.
Решение. Чтобы ответить на вопрос задачи, надо определить, каким может быть x и каким может быть y в данных отношениях.
а) Левая и правая части соотношения x2 = y2 могут быть толь-
ко неотрицательными числами, но x и y, очевидно, любые числа. Поэтому D(M ) = и E(M ) = .
— 238 —
б) Предположим вначале, что отношение задается не неравенством y >x2 , а равенством y =x2 , тогда график отношения пред-
ставляет собой обыкновенную «школьную» параболу. Известно из школы, что область определения параболы — множество всех чисел , а множество значений — множество неотрицательных чисел + {0}. Поскольку у нас требуется, чтобы y было больше
x, то графиком отношения будет часть плоскости, расположенная выше параболы (сама парабола в это множество не входит, т. к. y строго больше x). Тогда D(T ) = (множество всех чисел),
E(T ) =+ (множество всех положительных чисел).
Задача 3. Построить графики отношений, найти области определения и множества значений:
а) x + y =2 ; б) x = y2 .
Решение.
а) Вначале раскроем модули (школьный материал). Получим
x+y, при x ≥0 и
−x+ y, при x <0 и x + y =
−x− y, при x <0 и
x−y, при x ≥0 и
y ≥0
y ≥0 y <0 .
y <0
Каждый из четырех полученных вариантов в фигурных скобках соответствует какой-либо четверти координатной плоскости. Значит, надо построить в каждой координатной четверти линии, задаваемые полученными уравнениями. Так, например, в первой четверти следует построить линию x + y =2 , во второй — линию
−x+y =2 и т. д. В итоге получается график отношения, изображенный на рисунке.
— 239 —
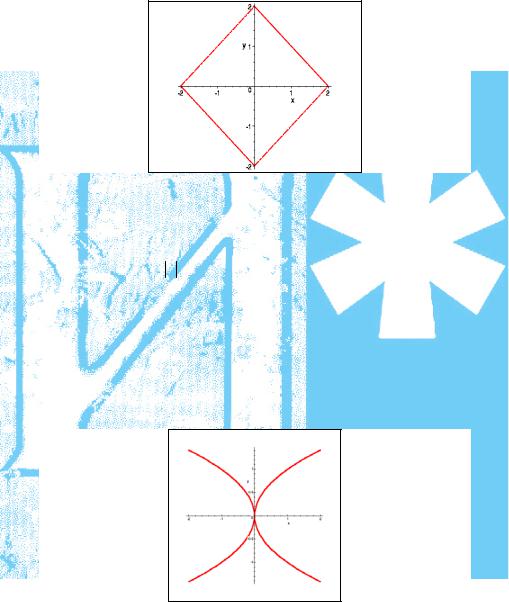
Область определения и область изменения этого отношения одинаковы D =E =[−2; 2] , что хорошо видно и по рисунку.
б) Раскроем модуль
x −y2
2
, при x ≥0
x−y
=
2
, при x <0.
−x−y
Первый из вариантов соответствует правой координатной полуплоскости, второй вариант — левой. Таким образом, получаем
2
, при x ≥0
y
x =
2
, при x <0.
−y
Строим график.
— 240 —
Область определения и множество значений этого отношения — все действительные числа.
Задача 4. Дано множество M ={1, 2, 3, 4, 5}. Составить матри-
цы отношений R и T, если R — «быть делителем», T — «иметь общий делитель, отличный от единицы».
Решение. Отношение
R ={(x, y) M 2 : x−делитель} выполняется для пар
(1,1),(1,2),(1,3),(1,4),(1,5), .
(2,2),(2,4),(3,3),(4,4),(5,5)
Каждой из этих пар в матрице отношения должна соответствовать единица, остальным парам — нуль. Получаем матрицу
1
2
3
4
5
1
1
1
1
1
1
2
0
1
0
1
0
.
3
0
0
1
0
0
4
0
0
0
1
0
5
0
0
0
0
1
Отношение
2
T =(x, y) M
: x и y имеют общий вид
делитель, отличный от 1
выполняются для пар {(2,2),(2, 4),(3,3),(4,4),(5,5)}. Матрица отношения имеет вид
— 241 —
1
2
3
4
5
1
0
0
0
0
0
2
0
1
0
1
0
.
3
0
0
1
0
0
4
0
0
0
1
0
5
0
0
0
0
1
Задача 5. Отношения заданы на множестве элементов структуры, изображенной на рисунке.
Выписать пары элементов, для которых данные отношения выполняются.
а) T — быть непосредственно связанным с; б) S — быть начальником;
в) F — быть непосредственным начальником.
Решение.
а) Отношение T выполняется лишь для тех пар элементов, которые непосредственно связаны между собой отрезком.
б) Данный элемент находится в отношении S с другим элементом, если существует восходящая ломаная линия, соединяющая
данный элемент с другим. Например, (k,b) S , а (k,c) S .
в) Упорядоченная пара элементов принадлежит отношению F, если они непосредственно связаны отрезком, причем первый эле-
мент пары лежит ниже. Например, ( f ,c) F , а (c, f ) F . Легко видеть, что отношение F является частью T.
— 242 —
Задача 6. Отношения A и B заданы на четырехэлементных множествах матрицами. Найти матричную запись отношений A B, A∩B и AB и построить их графы, если
1 0 0 1
0 1 0 0
0 1 1 1
0 1 1 0
A=
, B =
.
0 0 1 0
0 0 1 1
1 0 1 0
0 0 0 1
Решение. Используем правила булевой арифметики и определения указанных отношений. Имеем
1+0
0+1
0+0 1+0 1 1 0 1
+0
1+1
1+1
0
1+0 0 1 1 1
A B =
+0
0+0
1+1
0
=
,
0
+1 0 0 1 1
0+0
1+0
0
1+0
+1 1 0 1 1
1 0
0 1
0 0 1 0 0 0
0
0
1 1
1
0 0
1 1 1 0 0 1
0
A∩B =
1 1
=
0
1
,
0 0 0 0
0 1 0
0
0
0
1 0 0 0
1 0 0 1 0
0
0
1
0
1
4
AB =
∑(ain bnj )
= 0 1
1
1 .
0
1
n=1
0
1
1
1
0
1
— 243 —
Теперь построим графы полученных отношений.
1
2
1
2
1
2
3
4
3
4
3
4
Задача 7. Пусть B — отношение «быть братом», C — отношение «быть сестрой». Описать отношения:
а) B C ; б) B ∩C .
Решение.
а) Объединение двух данных отношений означает «быть братом или сестрой».
б) Пересечение этих отношений должно бы значить «быть братом и сестрой». Очевидно, такое отношение на множестве людей невозможно, т. е. в данном случае B∩C = (пустое отношение).
Задача 8. Являются ли отношения A B, A∩B и AB задачи 6
рефлексивными?
Решение. Отношение P рефлексивно, если для всякого элемента x множества (на котором отношение определено) выполнено xPx. Для матрицы такого отношения это означает наличие всех единиц на главной диагонали. Для графа — наличие петель у всех вершин. Легко видеть, что этим равносильным условиям удовлетворяет только первое отношение — A B .
Задача 9. Являются ли отношения «быть одногодком» и «быть квадратным корнем» рефлексивными, симметричными и транзитивными?
Решение. Отношение «быть одногодком» является симметричным, т. к. если x одногодок y, то y одногодок x; транзитивным, т. к. если x одногодок y, y одногодок z, то x одногодок z; рефлексивным, т. к. x, очевидно, одногодок x.
Отношение «быть квадратным корнем» не будет ни рефлексивным ( 2 ≠2 ), ни симметричным (т. к. из условия 4 =2 не сле-
— 244 —
дует 2 =4 ), ни транзитивным (т. к. из 2 = 4 и 4= 16 не выте-
кает, что 2= 16 ).
Задача 10. Записать матрицу для отношения, заданного на трехэлементном множестве, если это отношение:
а) только рефлексивно; б) только симметрично.
Решение.
а) Если отношение только рефлексивно, то всякий элемент множества находится в этом отношении только с самим собой, поэтому матрица должна содержать единицы только на главной диагонали.
б) Если отношение только симметрично, то: 1) в матрице имеется непустое количество единиц; 2) матрица симметрична относительно главной диагонали.
Теперь запишем матрицы
1
0
0
0
1
0
а) 0 1
0 ;
б) 1 0 1 .
0
1
0
1
0
0
Задача 11. Определить свойства отношений:
а) F — «быть меньше» на множестве всех действительных чисел;
б) T — «проживать в одном доме» на множестве людей;
в) S — «быть начальником» на множестве элементов структуры (задача 5).
Решение.
а) F ={(x, y): x < y}. Это отношение не рефлексивно, т. к.
x <x
не выполнено; антирефлексивно; не симметрично, т. к. из
x< y
не следует y <x ; асимметрично, т. к. из двух соотношений
x< y и y <x по крайней мере одно не выполнено; не антисимметрично; транзитивно, т. к. из x< y и y <z следует x <z .
Таким образом, это отношение строгого порядка.
— 245 —
б) T ={(x, y): x живет в одном доме с y}. Это отношение реф-
лексивно, т. к. xTx верно для любого x; не антирефлексивно; симметрично, т. к. из xTy следует yTx ; не асимметрично; не анти-
симметрично, т. к. xTy и yTx имеет место и для x≠ y ; транзитивно, т. к. если xTy и yTz , то xTz . Таким образом, это отношение эквивалентности.
в) S ={(x, y): x начальник y}. Отношение не рефлексивно, т. к.
бессмысленно выражение x начальник x; антирефлексивно; не симметрично, т. к. если x начальник y, то y не начальник x; асимметрично, т. к. из двух соотношений xSy и ySx , по крайней мере,
одно не выполнено; транзитивно, т. к. если x начальник y и y начальник z, то x начальник z.
Задача 12. Являются ли следующие отношения отношениями эквивалентности:
а) отношение подобия на множестве всех плоских треугольников;
б) отношение «быть супругом» на множестве всех людей; в) отношение параллельности на множестве всех прямых в про-
странстве?
Решение. Чтобы ответить на эти вопросы, надо проверить для указанных отношений выполнение трех свойств: рефлексивности, симметричности и транзитивности.
а) Всякий треугольник подобен сам себе, поэтому рефлексивность выполняется; если треугольник ABC подобен треугольнику MNK, то треугольник MNK подобен треугольнику ABC, поэтому симметричность выполняется; легко видеть, что выполняется и транзитивность. Отношение подобия есть отношение эквивалентности.
б) Рефлексивность не выполнена, т. к. выражение «x супруг x» бессмысленно; если x супруг y, то верно, что y супруг x, поэтому симметричность выполняется; если x супруг y, а y супруг z, то неверно, что x супруг z — транзитивность не выполняется. Отношение «быть супругом» не является отношением эквивалентности.
— 246 —
в) Всякая прямая параллельна самой себе, поэтому рефлексивность выполнена; если прямая x параллельна прямой y, то и прямая y параллельна прямой x, поэтому симметричность также выполнена; транзитивность, в свою очередь, тоже выполняется, значит, отношение параллельности прямых является отношением эквивалентности.
РАЗДЕЛ II
1. Предел и непрерывность
Задача 1. Является ли последовательность an =3nn++21 моно-
тонной?
Решение. Найдем «следующий» член последовательности, т. е. an+1 . Чтобы это сделать, надо подставить в формулу n-го члена n + 1
Теперь найдем разность an+1 −an и исследуем ее знак для про-
извольных n N . Легко понять, что если эта разность имеет один и тот же знак для всех возможных n, то последовательность монотонна. Имеем
a
−a
=
3n+4
−
3n+1
=
5
.
n+1
n
n+3
n+2
(n+3)(n+2)
Числитель — положительное число, а знаменатель — произведение натуральных чисел, значит, вся дробь также положительна. Отсюда следует, что an+1 >an для всех n, т. е. последовательность
монотонна (возрастает).
Задача 2. Показать, что предел последовательности an =3n+1 n+2
равен 3.
— 247 —
Решение. Рассмотрим
a −3
=
3n+1
−3
=
−
5
=
5
. За-
n
n+2
n+2
n+2
дадим некое сколь угодно малое положительное число ε
и опреде-
лим, при каких n выполняется неравенство
an −3
<ε. Имеем
a −3
=
5
<ε n>
5−2ε
.
n
n+2
ε
5−2ε
Значит, если взять номер n0
(квадратными скобками
=
ε
обозначается целая часть числа), то для всех n >n0 an будет нахо-
диться на расстоянии менее ε от числа 3, что и означает lim an =3 .
Задача 3. Найти следующие пределы функций:
n→∞
а) lim
x2 −9
; б) lim
2x4 −x2
; в) lim
x−1−2
.
x2 −x−6
x2
−2x−15
x→3
x→∞ 3x2 +x+3
x→5
Решение.
а) При подстановке значения x =3 получается неопределен-
0
ность вида . Разложив числитель и знаменатель на множители
0
и, сократив, получим
lim
x2 −9
=lim
(x−3)(x+3)
=lim
x+3
=lim
3+3
=
6
.
x2 −x−6
(x−3)(x+2)
x+2
3+2
5
x→3
x→3
x→3
x→3
б) При подстановке x =∞ получается неопределенность вида
∞
. Найдем старшую степень x (четвертая) и разделим почленно
∞
числитель и знаменатель на x4 . Получаем
— 248 —
2x4 −x2
2−
1
2−0
∞
x2
lim
=
=lim
=lim
=∞.
1
3
+0+0
x→∞ 3x2 +x+3
∞ x→∞ 1
x→∞ 0
+
+
x2
x3
x4
Теперь вновь подставим вместо
x
∞. В числителе остается
2−б м , а в знаменателе — сумма бесконечно малых. Результат:
предел равен бесконечности.
в) При подстановке x =5 вновь получается неопределенность
0
вида . Чтобы ее раскрыть, домножим числитель и знаменатель
0
на выражение, сопряженное числителю, затем разложим на множители и сократим. Имеем
x−1−2
0
( x−1−2)( x−1+2)
lim
=
=lim
=
x2 −2x−15
0
(x2 −2x−15)(
x−1+2)
x→5
x→5
lim
x−1−4
=lim
x−5
=
2
−2x−15)(
x−1+2)
x−5
)(
x+3
)
( x−1+2)
x→5
x→5 (
(x
lim
x−5
=lim
1
=
1
.
(x+3)( x−1+2)
32
x→5 (x−5)(x+3)( x−1+2)
x→5
Задача 4. Найти следующие пределы функций:
а) lim
tgx2
; б)
lim
2x
; в)
limsin
1
; г) lim
sin 2x
.
x→0
1−cos x
x→0
3
1+x −1
x→0
x
x→0
(
)
ln 1+x
Решение.
0
а) При подстановке возникает неопределенность вида .
0
Воспользуемся формулами тригонометрии, затем эквивалентностью бесконечно малых. Имеем
— 249 —
lim
tgx2
=lim
tgx2
=lim
x2
=lim
2x2
=2 .
1−cos x
2 x
x
2
x2
x→0
x→0
2sin
x→0
x→0
2
2
2
б) Здесь также неопределенность вида
0
0
. Домножим числи-
тель и знаменатель дроби на выражение
3 (1−x)2 +3 (1−x)+1,
чтобы в знаменателе получилась разность кубов, затем сократим.
2x
2x
3 (1−x)2 +3
(1−x)+1
lim
=lim
(
)
=
(
)(
)
x→0 3 1+x −1
x→0
3
3 (1−x)2
1−x −1
+3 (1−x)+1
(
3
(1−x)2
)
(
3 (1−x)2
)
2x
+3 (1−x)+1
2
+3 (1−x)+1
lim
=lim
=−2 .
1−x−1
−1
x→0
x→0
в) Аргумент синуса при x →0 неограниченно возрастает, синус
при этом не стремится ни к какому пределу; limsin 1 — не суще-
x→0 x
ствует.
0
г) Для раскрытия неопределенности воспользуемся экви-
0
валентностью бесконечно малых. Имеем
lim
sin 2x
=lim
2x
=2 .
x
x→0 ln (1+x)
x→0
3
x
x+5
2x
Задача 5. Найти пределы: а) lim 1+
x
; б) lim
.
x→∞
x→∞ x−2
Решение.
а) Здесь имеется неопределенность вида (1∞). Воспользуемся вторым замечательным пределом. Имеем
— 250 —
x
x 3
3
3
x
1
1
=lim e
3
=e
3
lim 1+
.
x
=lim 1+
x
=lim 1+
x
x→∞
x→∞
x→∞
x→∞
3
3
б) Та же неопределенность и тот же способ вычисления предела. Имеем
x+5 2x lim x→∞ x−2
x−2+7
2x
7
2x
=lim
=lim 1+
=
x−2
x−2
x→∞
x→∞
x−2 14x
x−2
7
1
14x
=lim e x−2 =e14 .
=lim 1+
x−2
x→∞
x→∞
7
Задача
6. Определить
порядок
бесконечно
малой
α(x)= sin 2x
при
x →0
по
сравнению с бесконечно
малой
β(x) = x (x >0).
Решение.
Найдем
lim
sin 2x
. Здесь
неопределенность вида
x→0
x
0
раскрывается после тригонометрических преобразований.
0
Имеем
lim
sin 2x
=lim
2x
=lim
2
=∞.
x
x
x
x→0
x→0
x→0
Задача 7. Показать, что функция y = x−x 2 имеет разрыв в точ-
ке x =2 .
— 251 —
Решение. Найдем односторонние пределы функции в точке x =2 . Имеем
lim
x
= lim
2
=−∞,
x→2− x−2
x→2−−0
lim
x
= lim
2
=+∞.
x→2+ x−2
x→2++0
Односторонние пределы равны бесконечности разных знаков,
поэтому функция
y =
x
в точке
x =2
имеет разрыв второго
x−2
рода.
Задача 8. Исследовать функцию
y
=
x2
−9
arctg
1
на не-
x−3
x−2
прерывность.
Решение. Вначале находим область определения этой функции
D( y)=(−∞;2) (2;3) (3;+∞).
Подозрительными «на разрыв» точками являются точки x =2 и
в) Эту функцию нельзя продифференцировать по таблице, поэтому применим специальный прием. Прологарифмируем равенст-
во y =xx2 по основанию e (это возможно, т. к. обе его части положительны). Получим
ln y =ln xx2 ln y =x2 ln x .
Теперь продифференцируем последнее равенство по x и получим
1y y′=2x ln x+x2 1x .
Откуда y′= y(2xln x+x)=xx2 (2ln x+1)x =xx2+1 (2ln x+1).
— 253 —
Задача 2. Найти производную
dy
из уравнения
dx
y2 +xy +x2 =0.
(*)
Решение. Говорят, что уравнение ( ) задает функцию
y(x) не-
явно. Мы считаем, что эта функция дифференцируема. Продифференцируем равенство ( ) по x и получим
2 yy′+ y +xy′+2x =0 .
Из этого равенства легко выразить производную y′. Действительно, после элементарных действий приходим к соотношению
y′=−2yy++2xx .
Задача 3. Окружность единичного радиуса задана параметрическими уравнениями
y =sin t
, t R .x =cost
Найти производную y′x = ddxy .
Решение. Распишем дифференциалы в последней формуле и получим
y′
=
dy
=
yt′dt
=
yt′
=
cost
=−ctg t .
dx
x′dt
x′
x
−sin t
t
t
Задача 4. Найти dy и d 2 y , если y =x(ln x−1).
Решение. Используя определение дифференциала, получаем
dy = y′dx =(x(ln x−1))′dx =(ln x−1+1)dx =ln xdx , d 2 y =d (dx)= y′′(dx)2 =(dxx)2 .
— 254 —
Задача 5. Найти промежутки монотонности и экстремумы
функции y =
x
.
ln x
Решение.
Функция определена при x (0;1) (1;∞). Следует
определить критические точки производной и ее промежутки знакопостоянства. Имеем
y′=
ln x−1
; y′=0 x =e ; x =1 — точка разрыва второго ро-
ln2 x
да; y′<0 при x (0;1) и x (1;e), y′>0 при x (e;∞).
Вывод. Функция убывает при x (0;1) и при x (1;e)
и воз-
растает при x (e;∞); x =e — точка минимума, y(e)=e .
Задача 6. Найти асимптоты кривой y =2x−
cos x
.
x
Решение. Область определения D( y)=(−∞;0) (0;∞),
значит,
в точке x =0 может быть вертикальная асимптота. Найдем односторонние пределы. Имеем
cos x
cos x
lim 2x−
=+∞,
lim 2x−
=−∞.
x
x→0−
x
x→0+
Действительно,
асимптота
x =0 есть. Находим наклонные
асимптоты. Имеем
2x−
cos x
cos x
k = lim
x
= lim 2
−
=2 ,
1
x→−∞
x
x→−∞
x2
cos x
b1 = lim 2x−
−2x =0 ;
x
x→−∞
2x−
cos x
cos x
k2
x
= lim
= lim 2
−
x2
=2
,
x
x→+∞
x→+∞
— 255 —
cos x
b2
= lim 2x−
−2x =0 .
x
x→+∞
Поскольку коэффициенты получились попарно одинаковыми, то имеется одна наклонная асимптота для обеих ветвей графика y =2x .
Вывод. Кривая имеет одну вертикальную асимптоту (x =0) и одну наклонную асимптоту ( y =2x) .
Задача 7. Найти промежутки выпуклости и вогнутости, а также точки перегиба кривой y =xex .
Решение. Область определения функции — вся числовая прямая. Найдем вторую производную
y′′=(xex )′′=ex (2+x),
иприравняв ее к нулю, получим единственную критическую точку
x=−2 . Легко видеть, что y′′<0 при x <−2 и y′′>0 при x >−2 .
Значит, при x <−2 график выпуклый, при x >−2 — вогнутый, а
2
точка −2;−
— точка перегиба.
e2
Задача 8. Найти область определения следующих функций:
а) u = x2 + y2 −1 ; б) z =
x
; в) u =arcsin(x+y) .
y
Решение.
а) x2 +y2 −1≥0 x2 +y2 ≥1. Область вне круга (вместе с ок-
ружностью) с центром в начале координат и радиусом 1.
б) Область, включающая первую и третью четверти, без оси Ox и начала координат.
в) −1≤x+ y ≤1. Полоса между двумя прямыми: y =−1−x и y =1−x .
Задача 9. Найти дифференциал функции z =arctg xx−+ yy .
— 256 —
Решение. Используем формулу dz =
∂z
dx+
∂z
dy . Вначале
∂x
∂y
найдем
частные производные:
∂z
=
y
,
∂x
x2 +y2
Затем
подставим
их
в
формулу
∂z
x
=−
.
∂y
x2 +y2
иполучим
∂z
∂z
y
x
dz
=
dx+
dy =
dx−
dy .
∂x
∂y
x2 +y2
x2 +y2
Задача
10.
Найти
экстремумы
функции
z =x2 +xy +y2 −3x−6y .
Решение.
Найдем
частные производные:
∂z
=2x+y−3 ,
∂z
∂x
=x+2 y−6 . Теперь отыщем критические точки,
согласно не-
∂y
обходимому условию
2x+ y−3=0
x =0
+2 y−6=0
x
y =3.
Находим значение дискриминанта ∆= AC −B2 в точке (0;3).
∂2 z
=2
,
∂2 z
=2
,
∂2 z
=1 ∆= AC −B2
=2 2−1=3>0
и
∂x2
∂y2
∂x∂y
A>0 .
Значит, в точке (0;3) функция имеет минимум z(0;3)=−9 .
3. Интеграл
Задача 1. Найти следующие интегралы:
а) ∫
dx
; б) ∫x cos(x2 )dx ; в) ∫
xdx
; г)
∫ 1−x2 dx .
x ln x
2
x −1
Решение (все интегралы в этой задаче не табличные):
— 257 —
а) Заметим, что d (ln x)=
dx
, поэтому интеграл можно перепи-
x
d (ln x)
dt
сать в виде ∫
, т. е. он сводится к табличному ∫
. Итак,
ln x
t
∫xdxln x =∫d (lnlnxx)=ln ln x +C .
б) «Задвинем»
x за знак дифференциала, используя равенство
xdx =
1
d (x2 ) и
получим ∫xcos(x2 )dx =∫cos(x2 )
1
d (x2 )=
2
2
=12 ∫cos(x2 )d (x2 ). Последний интеграл табличный. В результате получаем ∫xcos(x2 )dx =12 sin(x2 )+C .
в) Заметим, что xdx =12 d (x2 )=12 d (x2 −1). Это позволяет све-
сти интеграл к табличному.
Имеем
∫
xdx
1
∫
d (x2 −1)
=
=
2
−1
2
2
1
x
x
−1
=
ln
x2 −1
+C .
2
u = 1−x2 ,
г) Применим метод «по
частям».
Обозначим
dv =dx . Тогда v = x и du =−
xdx
, и формула «по частям» дает
1−x2
∫ 1−x2 dx =x 1−x2 +∫
x2dx
.
1−x2
Последний интеграл представим следующим образом:
— 258 —
x2dx
1−x2 −1
=−∫ 1−x2 dx+∫
dx
∫
=−∫
.
1−x2
1−x2
1−x2
Таким образом, приходим к равенству
∫ 1−x2 dx =x 1−x2 +arcsin x−∫
1−x2 dx .
Остается выразить из этого равенства искомый интеграл. Имеем
∫ 1−x2 dx =
1
x 1−x2 +
1
arcsin x+C .
2
2
Задача 2. Найти интегралы:
а) ∫sin xdx ; б) ∫
x4 −2x2 +2
dx ;
в) ∫
dx
.
2x−3
4sin x+3cos x+5
Решение.
а) Введем новую переменную t = x ; тогда x =t2 и dx =2tdt . Поэтому подынтегральное выражение примет вид 2t sin tdt . Полученный интеграл находим методом «по частям», при этом u =2t ,
dv =sin tdt . Имеем
∫2t sin tdt =2sin t −2t cost +C =2sin
x −2 x cos
x +C .
б) Вначале поделим уголком числитель на знаменатель, чтобы
выделить целую часть. Получим
x4 −2x2 +2
=
x3
+
3x2
+
x
+
3
+
41
.
2x−3
2
4
8
16
16
(2x−3)
Теперь можно почленно проинтегрировать полученную сумму. Имеем
x
3
3x
2
x
3
41
+
+
+
+
dx =
∫
2
4
8 16 16
(2x−3)
— 259 —
= x4 + x3 + x2 +3x + 41 ln 2x−3 +C . 8 4 16 16 32
в) Тригонометрическую подынтегральную функцию сведем к рациональной дроби путем так называемой универсальной подстановки:
t =tg
x
,
sin x =
2t
, cos x
=
1−t2
,
x =2arctgt ,
dx =
2dt
.
2
1+t2
1+t2
1+t2
В результате этих замен получим интеграл
∫
2dt
=∫
dt
=−
1
+C =−
1
+C .
2t
2
+8t +8
(t +2)
2
t +2
tg
x
+2
2
Задача 3. Найти интегралы:
3x−1
а) ∫
x+2
dx ; б) ∫
dx .
2
2x2 −10x+16
x
−4x+13
Решение.
а) Заметим, что в числителе многочлен первой, а в знаменателе — второй степени, поэтому вначале находим дифференциал знаменателя. Имеем
d (x2 −4x +13)=(2x−4)dx .
Теперь распишем интеграл следующим образом:
∫
x+2
dx =
1
∫
2(x +2)
dx =
x
2
−4x +13
2
2
x
−4x +13
=
1
∫
2x−4+8
dx =
1
∫
2x−4
dx+
1
∫
8
dx =
2
2
2
2
2
−4x+13
x −4x+13
x −4x+13
2
x
=
1
∫
d
(x2 −4x+13)
+4∫
dx
=
2
2
−
4x+13
x
2
x
−4x+4+9
— 260 —
=1 ln x2 −4x+13 +4∫ dx = 2 (x−2)2 +32
=12 ln x2 −4x+13 +43 arctg x−3 2 +C .
б) Применим аналогичный метод. Имеем
d (2x2 −10x +16)=
=(4x−10)dx . Преобразуем интеграл.
4x−10
26
∫
3x−1
dx =
3
∫
+
3
dx =
2x2 −10x+16
4
2x2 −10x+16
=
3
∫
d (2x2 −10x+16)
+
13
∫
dx
=
4
2x2 −10x+16
2
2x2 −10x+16
=
3
2x2 −10x +16 +
13
∫
dx
=
2
2 2
x2 −5x+
25
+
7
4
4
=
3
2x2 −10x +16
+
13
∫
dx
=
2
2
2
5
2
7
x−
2
+
4
3
2x2
13
5
x2 −5x+8
=
−10x +16 +
ln
x−
+
+C .
2
2
2
2
3
Задача
4. Вычислить
интегралы:
а) ∫x2 x3 dx ;
2
2
x2 −3x+1
б) ∫
dx .
x
1
— 261 —
Решение.
а) Воспользуемся таблицей и формулой Ньютона–Лейбница.
3
3
7
9
3
x2
∫x2
x3 dx =∫x2 dx
=
=
9
2
2
2
2
3
2
( 39 −
29 )=
2
2
32
2
x9
(92 3 −24
2)=18 3 −
.
=
2 =
9
9
9
9
б) Путем преобразования подынтегрального выражения, сведем интеграл к табличным.
2
x2 −3x+1
2
2
2 dx
∫
dx =∫xdx−3∫dx+∫
=
x
x
1
1
1
1
x2
2
2
2
1
=
−3x
+ln x
=2
−
−6+3+ln 2−0=
2
1
1
2
1
=ln 2−32 .
Задача 5. Вычислить следующие интегралы: а)
1
б) ∫x arctg xdx .
−1
Решение.
d (x2 )
1
xdx
1
1
1
arctg x2
1
π
а) ∫
=
∫
=
=
.
1+x
4
2
1+x
4
2
8
0
0
0
б) Применяем метод «по частям».
∫1 xdx
0 1+x4 ;
— 262 —
u =arctgx , du =
dx
,
dv =xdx
,
v =
x2
,
1+x2
2
тогда
1
x2
1
1
x2dx
∫x arctg xdx =
arctg x
−∫
=
2
−1
2
−1 −1 2
(1+x
)
1
π
π
1
1
=
+
−
1−
dx =
8
8
2
1+x2
−∫1
π
x
1
1
arctg x
1
π
−1+
π
π
−1 .
=
−
+
=
=
4
2
2
4
4
2
−1
−1
Задача 6. Вычислить интегралы методом замены переменной:
e
π
1
ln x
∫2
(а) ∫
dx ; (б)
sin2 x cos xdx ; (в)
∫ 1−x2 dx .
1
x
0
0
Решение.
а) Пусть ln x =t , тогда dt =dxx , но подставлять это в интеграл
нельзя, т. к. должны поменяться пределы. Имеем tн =ln xн =ln1=0 , tв =ln xв =ln e =1 .
Теперь можно записать преобразованный интеграл в виде
1
3
1
2t 2
2
∫
tdt =
=
.
3
3
0
0
— 263 —
б) Пусть sin x =t . Тогда
dt =cos xdx ,
tн =sin xн =sin 0=0 ,
t
в
=sin x
=sin
π
=1 и интеграл имеет вид
в
2
π
1
1
2
t3
1
∫sin2 x cos xdx =∫t2dt =
=
.
3
3
0
0
0
Конечно, эти интегралы можно вычислить и не прибегая к за-
мене переменной.
в) Неопределенный интеграл уже находился ранее методом «по
частям».
Пусть
теперь
x =sin t ,
dx =cos tdt , t =arcsin x ,
tн =arcsin 0=0 ,
tв =arcsin1=
π
.
Очевидно,
что
2
1−sin2 t = cos2 t =cost ,
т. к.
t изменяется в первой четверти.
Имеем
ππ
π
2
1
2
1
π
∫cos2 tdt =
∫(1−cos 2t)dt =
(t −sin 2t)
02 =
.
2
2
4
0
0
Задача 7. Вычислить несобственные интегралы (или устано-
+∞
x
0
dx
вить их расходимость): (а)
∫
arctg
dx ; (б) ∫
.
2
2
Решение.
0 1+x
−∞ 4+x
+∞
x
+∞
а) ∫
arctg
dx = ∫arctg xd (arctg x)=
2
0 1+x
0
π 2
2
b
arctg0
π
2
arctg
2
=lim
−
=
−0
=
.
2
2
8
b→∞ 2
Поскольку предел оказался конечным, то интеграл сходится.
— 264 —
0
dx
1
1
a
π
б) ∫
= lim
arctg 0
−
arctg
=
.
2
2
2
2
4
−∞ 4+x
a→−∞
Поскольку предел оказался конечным, то интеграл сходится. Задача 8. Вычислить несобственные интегралы (или устано-
1
dx
1
dx
вить их расходимость): (а) ∫
; (б) ∫
.
2
0
x(1−x)
−1 x
Решение.
а) Вначале выделим полный квадрат в подкоренном выражении.
1
dx
1
dx
1
dx
∫
=∫
=∫
=
x(1−x)
2
0
0
2
−x+
1
−
1
0
1
1
2
− x
4
4
2
− x−
2
=lim arcsin (2x−1)
1−ε
=lim(arcsin(1−2ε)−arcsin (2ε−1))=π.
ε→0
0+ε
ε→0
Вновь получился конечный предел, поэтому интеграл сходится.
1
dx
0
dx
1
dx
0−ε
dx
1
dx
б)
∫
=∫
+∫
=lim
∫
+lim ∫
=
2
2
2
2
2
−1 x
−1 x
0
x
ε→0
−1
x
ε→0 0+ε x
1
1
1
1
=lim −
+
+lim −
+
=∞.
0−ε
0
ε→0
−1
ε→0
1
+ε
Предел равен бесконечности, поэтому интеграл расходится.
РАЗДЕЛ III Элементы теории вероятностей
Задача 1. Сколькими способами можно расставить 5 книг на книжной полке?
Решение. Речь идет о количестве перестановок из пяти элементов. Применим формулу для числа перестановок
— 265 —
P5 =5!=1 2 3 4 5=120 .
Задача 2. В бригаде из 20 человек требуется выделить пятерых для работы на определенном участке. Сколькими способами это можно сделать?
Решение. Так как порядок выбранных пяти человек не имеет значения, то следует применить формулу числа сочетаний. Имеем
C205 =
20!
=
1 2 ... 15 16 17 18 19 20
=
5! (20−5)!
1 2 ... 5 1 2 ... 15
=16 17 18 19 20 =15504 . 1 2 3 4 5
Задача 3. Из 12 человек нужно выбрать 4 человека и разместить их на четырех занумерованных стульях. Сколькими способами это можно сделать?
Решение. Так как стулья занумерованы, то порядок размещения четырех человек важен. Применяем формулу для числа размещений
A4
=
12!
=
1 2 ... 8 9 10 11 12
=
12
(12−4)!
1 2 ... 7 8
=9 10 11 12 =11880 .
Задача 4. Проверить следующие соотношения между случайными событиями:
а) ¬(A+B)=¬(AB);
б) (A+B)−B =A−AB ;
в) ¬A+¬B =¬(AB).
Решение. Первое соотношение неверно, т. к. отрицание суммы, в общем случае, есть часть отрицания произведения. Это хорошо видно на диаграммах.
— 266 —
Второе соотношение верно (см. диаграммы).
В обоих случаях в итоге получается серп A (слева).
Третье соотношение — это закон де Моргана, поэтому выполняется.
Задача 5. Пусть A, B и C — три произвольных события. Найти выражения для событий, состоящих в том, что из A, B, C:
а) все три события произошли; б) ни одно событие не произошло; в) произошло только A;
г) произошло одно из трех событий (безразлично какое). Решение. События A, B и C произвольны, значит, каждое из них
может произойти как отдельно от остальных, так и с каждым вместе. Таким образом, это соответствует стандартной позиции в расположении множеств (интерпретирующих события) на диаграмме Венна.
— 267 —
A B
C
а) Здесь происходят все три события одновременно, это соответствует множеству A∩B ∩C (или ABC) на диаграмме (темная лунка). Запись этого события — ABC.
A B
C
б) В этом случае не происходит ни одно из событий A, B и C; это соответствует части прямоугольника, за исключением всех трех
кругов. Запись этого события ¬(A B C).
A B
— 268 —
C
в) В этом случае событие A происходит, но события B и C не происходят. Это соответствует той части круга A, которая не вхо-
дит ни в B, ни в C. Запись этого события A¬(B C).
Задача 6. Бросаются две игральных кости. Пусть событие A заключается в том, что сумма очков четная, а B состоит в том, что выпала хотя бы одна единица. Описать пространство элементарных событий, события A+B , A¬B . Найти вероятности этих событий, если все элементарные исходы равновероятны.
Решение. Элементарный исход (событие) в данном испытании состоит в выпадении конкретных чисел на двух игральных костях. Так как на каждой кости имеется шесть граней с шестью числами от 1 до 6, то всевозможных сочетаний чисел на двух костях будет 36. Таким образом, пространство элементарных событий имеет вид:
Ω={(ω1, ω2 ): ω1, ω2 =1,2,3,4,5,6,}.
Изобразим пространство элементарных исходов при однократном подбрасывании двух игральных костей в виде таблицы упорядоченных пар чисел, обозначающих число выпавших очков на первой и второй кости соответственно.
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
— 269 —
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
(4,6)
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
(5,6)
(6,1)
(6,2)
(6,3)
(6,4)
(6,5)
(6,6)
Событие A состоит в выпадении четной суммы очков, поэтому ему благоприятствуют такие исходы (элементарные события), в которых ω1 и ω2 либо оба четные, либо оба нечетные. Нетрудно
понять, что всего таких исходов будет 18. В таблице такие исходы подчеркнуты.
Событие B состоит в выпадении хотя бы одной единицы. Предположим, что на первой кости выпала единица. Тогда на второй кости может выпасть любое число — всего таких исходов 6. Теперь пусть на второй кости выпала единица. Тогда на первой также может быть любое число. Всего таких исходов 6. Объединив эти ис-
ходы и вычитая исход (1,1), который встретился дважды, получим
число исходов, благоприятствующих событию B (11). В таблице эти исходы напечатаны курсивом.
Событие A+B состоит в выпадении четной суммы очков или хотя бы одной единицы. К 18 исходам, благоприятствующим событию A, прибавим исходы, благоприятствующие событию B, за
исключением тех, которые уже вошли в A (например, исход (1,3)),
т. е. исходы (1,2), (1,4), (1,6), (2,1), (4,1), (6,1). Получится
18+11−5=24 благоприятствующих исхода для события A+B . Количество исходов, благоприятствующих событию A+B , легче подсчитать в таблице. Для этого нужно учесть исходы, подчеркнутые и напечатанные курсивом. Согласно классической формуле, получим вероятность P(A+B)=3624 = 23 .
Проведем рассуждения для события A¬B . Это событие состоит в выпадении четной суммы, причем среди чисел не должно быть единиц. В таблице сосчитаем пары чисел, которые подчеркнуты, но не напечатаны курсивом. Видно, что таких исходов будет 13. Получаем вероятность события A¬B .
— 270 —
P(A¬B)=1336 .
Задача 7. В корзине 15 одинаковых по размерам и весу шариков, из которых 9 красных и 6 белых. Из корзины извлекается один шар. Какова вероятность, что он окажется белым?
Решение. Обозначим буквой A событие, заключающееся в извлечении белого шара. Данное испытание имеет 15 равновозможных элементарных исходов, из которых 6 благоприятствуют событию A. Поэтому
P(A)=156 =53 .
Задача 8. Из стандартной колоды карт (36 шт.) вынимается одна карта. Какова вероятность, что она не старше десятки?
Решение. Обозначим искомое событие буквой B. В стандартной колоде имеется 20 карт не старше десятки (6, 7, 8, 9, 10 в каждой из четырех мастей). Поэтому вероятность события B равна
P(B)=3620 =95 .
Задача 9. На шести одинаковых карточках написаны буквы Е, Н, Ь, Ю, Т, М. Карточки перемешивают и раскладывают наугад в ряд. Какова вероятность, что при этом получится слово ТЮМЕНЬ?
Решение. Очевидно, имеется только один благоприятствующий вариант такого расположения карточек. Всего же вариантов столько, сколько существует перестановок из 6 элементов, т. е.
P6 =6!=720 . Искомая вероятность 7210 ≈0,001389 (или 0,14% ).
Задача 10. На электростанции 15 сменных инженеров, из них 3 женщины. В смену занято 3 человека. Найти вероятность того, что в случайно выбранную смену мужчин окажется не менее двух.
Решение. В случайно выбранной смене мужчин может оказаться трое, двое, один и ни одного. По условию нас интересуют первые два случая. Обозначим через A событие, состоящее в том, что
всмене трое мужчин, через B событие, состоящее в том, что в сме-
—271 —
не двое мужчин. Легко видеть, что события A и B несовместны, т. к. в одной смене не может оказаться одновременно 2 и 3 мужчины. В задаче требуется определить вероятность события A+B . По формуле вероятности суммы двух несовместных событий имеем
P(A+B)=P(A)+P(B).
Используем классическую формулу для нахождения этих вероятностей. Число всех возможных вариантов составления смен ин-
женеров равно C153 =3!15!12! . Число вариантов, благоприятствующих
событию A, равно C123 =3!12!9! (мы выбираем трех мужчин из двена-
дцати). Число вариантов, благоприятствующих событию B, равно C122 C31 = 2!12!10! 1!3!2! (мы выбираем одну женщину из трех и двух мужчин из двенадцати). Тогда искомая вероятность получается так:
Вероятность получилась достаточно большой, что и понятно, поскольку инженеров-мужчин на электростанции значительно больше.
Задача 11. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность, что точка попадет в квадрат? (геометрическая вероятность).
— 272 —
Решение. Обозначим радиус круга через R, сторону квадрата через a, S — площадь круга, S1 — площадь квадрата, A — попада-
ние точки в квадрат (событие). Тогда вероятность искомого события равна отношению площади квадрата к площади круга. Используя формулы школьной геометрии, получаем
P(A)=
a a
=
2R
2R
=
2
≈0,637 .
πR2
πR2
π
Задача 12. Вероятность попадания в мишень для первого стрелка равна 0,6 , а для второго — 0,8 . Найти вероятность того, что
после первого залпа будет хотя бы одно попадание в мишень. Решение. Пусть A — попадание в мишень первого стрелка,
B — попадание в мишень второго стрелка, C — попадание в мишень хотя бы одного стрелка. Ясно, что события A и B совместны и C = A+B . Используем формулу вероятности суммы двух совместных событий
P(C)=P(A)+P(B)−P(AB).
Поскольку события A и B независимы, то
P(AB)=P(A)P(B).
В результате получаем
P(C)=0,6+0,8−0,6 0,8=1,4−0,48=0,92 .
Задача 13. В урне 4 синих, 6 желтых и 5 красных шаров. Поочередно извлекаются наудачу 3 шара без возвращения. Найти ве-
— 273 —
роятность того, что первый шар будет красным (A), второй синим (B) и третий желтым (C) .
Решение. События A, B и C зависимы. Вероятность появления красного шара при первом извлечении P(A)=155 =13 . Вероятность
извлечь вторым синий шар будет условной (в предположении, что красный шар уже извлечен)
P(B | A)=144 =72 .
Вероятность извлечь третьим желтый шар также условная
P(C | AB)=136 .
По формуле умножения вероятностей зависимых событий получаем
P(ABC)=P(A)P(B | A)P(C | AB)=13 72 136 =914 .
Задача 14. Некий рабочий обслуживает 3 однотипных станка. Вероятность того, что любой станок сломается в течение часа, равна 0,2 (событие A). Определить вероятность того, что в течение
часа ни один из станков не сломается.
Решение. Вероятность того, что в течение часа любой из станков не сломается, находим по правилу вычисления вероятности противоположного события:
P(¬A)=1−P(A)=1−0,2=0,8 .
Чтобы в течение часа ни один из станков не сломался, необходимо произойти событию B =(¬A)3 . Вычисляем вероятность события B
P(B)=P((¬A)3 )=(P(¬A))3 =(0,8)3 =0,512 .
— 274 —
Задача 15. На сборку попадают детали с трех станковавтоматов. Известно, что первый станок дает 3% брака, второй — 4%, а третий — 5%. Найти вероятность попадания на сборку бракованной детали, если с первого станка поступило 500, со второго 300, а с третьего 200 деталей.
Решение. Эта задача решается с помощью формулы полной вероятности. Пусть событие A — деталь оказалась бракованной, B1 — деталь изготовлена на первом станке, B2 — на втором и
B3 — на третьем станке. Вероятности событий Bi вычисляем по классической формуле:
P(B )=
500
=
500
=
1
,
1
500+300+200 1000
2
P(B )=
300
=
3
, P(B )=
200
=
1
.
2
1000
10
3
1000
5
Условные вероятности
P(A | Bi )
в задаче
даны. Поскольку
A=B1 A+B2 A+B3 A , то
P(A)=P(B1 )P(A | B1 )+P(B2 )P(A | B2 )+
+P(B3 )P(A | B3 )=
=12 1003 +103 1004 +15 1005 =100037 =0,037=3,7% .
Задача 16. Пусть на сборку попала бракованная деталь. Определить вероятность, что она изготовлена на третьем станке (по условию предыдущей задачи).
Решение. Здесь надо использовать формулу Байеса. Требуется найти вероятность события B3 , при условии, что событие A про-
изошло. Имеем
P(B )P(A | B )
1
5
10
5
P(B | A)=
3
3
=
100
=
≈0,27 .
3
P(A)
37
37
1000
— 275 —
бДСДзаь Сгь лДейдйзнкйгь
íЦлнх Сгь лДейдйзнкйгь
1.Теория множеств
1.Пусть A={a : a =b+c, b,c B}, B ={−1,4}. Задать перечислением множество A :
1) {−2,3,8};
2){−2,3,−2,3,8,8};
3){3,3};
4){3,−3,−5,5}.
2. Задать с помощью характеристического свойства множество четных чисел, кратных четырем:
1){x : x 2n};
2){x : x =4k, k Z};
3){x : x =n+4, n N};
4){x : x=N / 4}.
3. Пусть U (универсальное множество) =[1,5] , A=(1,2). Найти множество ¬(U ∩ A) :
1)[2,5];
2)(2,5] ;
3)[3,5] ;
4){1} [2,5] .
4. Пусть A — произвольное множество. Выбрать верное соотношение:
1){0}= ;
2)0 ;
3)A ;
— 276 —
4) A .
5. Пусть A={1,3,5,7,9}, B={2,3,4,5}, U ={x : x N, x≤10}.
Найти U −(A B) :
1){6,7,8,9,10};
2){6,8,10};
3){6,8,9,10};
4){1,2,3,4,5}.
6. Дано: A={(x, y) : x2 = y2 }, B ={(x, y) : y =1}. Найти пересечение этих множеств:
1)множества не пересекаются;
2)множества пересекаются в единственной точке (1,1) ;
3)множества пересекаются в двух точках (−1,1) и (1,1) ;
4)множества пересекаются в четырех точках (−1,1), (−1,−1), (1,−1) и (1,1) .
7.Пусть A — множество сотрудников некоего вуза, а B — множество его преподавателей. Верно соотношение:
1)A∩B= ;
2)A B ;
3)A B ;
4)A=B .
8.Результат упрощения выражения ¬(A∩B) есть:
1)A B ;
2)A ∆ B ;
3)A∩B ;
4)¬A¬B .
9.Дано: A={−2;3;5}, B ={−3;5;−6;7}, C ={−3;−2;−1}. Най-
ти A∩B ∩C :
1){−3;−2;5};
—277 —
2){3,5};
3);
4){ }.
10. Равенство A∩B =B верно в случае, когда:
1)A B ;
2)B A ;
3)B−A= ;
4)A−B ≠ .
11. Определить отношение между множествами: A={x : x2 −x−6=0} и B={x : x+2=0}.
1)A B ;
2)A−B = ;
3)B A ;
4)A B= .
12.Задать множество {x : x A или x B}:
1) {x : x A B}; 2) {x : x A∩B}; 3) {x : x A ∆ B};
4) {x : x ¬A и x ¬B}.
13.Пусть A={x : x =1}, B ={x : x ≥1}. Записать множе-
ство C = A∩B :
1)[−1;1] ;
2)(−1;1) ;
3)(−∞;−1) (1;+∞) ;
4){−1;1}.
14. Известно, что ¬A ¬B . Множества A и B находятся в отношении:
1) A B ;
— 278 —
2)A=B ;
3)B A ;
4)A= .
15. Результат упрощения выражения ¬(¬A∩B) есть:
1)A∩¬B ;
2)¬A B ;
3)¬A ¬B ;
4)A ¬B .
16. Пусть A={x : x =2n, n Z}, B ={x : x =4n, n Z}. Най-
ти A∩B :
1){x : x =4n, n Z};
2){x : x =6n, n Z};
3){x : x =5n, n Z};
4){x : x =−2n, n Z}.
17. Задать перечислением множество β( A) всех подмножеств множества A={−1;1}:
1){0};
2){{−1;1},{−1},{1}, };
3){{−1;1},{−1},{1},{ }};
4){[−1;1]}.
18. Дано: A={(x; y) : y =x2 −1}, B ={(x; y) : y =1−x2}. Найти A∩B :
1){(0;0)};
2){(1;1)};
3){(−1;0), (1;0)};
4){(0;−1), (0;1)}.
— 279 —
19. Даны произвольные множества A и B , такие, что ¬A∩¬B = . A−B и B−A представляют собой:
1)U и U ;
2)B и A ;
3)A и B ;
4)и .
20. Даны два множества A=[−3;5] и B =(−3;5). A ∆ B представляет собой:
1){−3};
2){5};
3)(−3;5) ;
4){−3;5}.
2.Основы математической логики
1.Среди следующих предложений найти высказывания: 1) всякий человек весит больше 150 кг; 2) привет, привет;
3) если данный треугольник прямоугольный, то у него есть ги-
потенуза;
4)стой, кто идет!
1)2, 4;
2)1, 3;
3)1, 2, 3, 4;
4)ни одно из перечисленных.
2.Среди следующих высказываний установить элементарные:
1)если данное число делится на 5, то оно делится на 10;
3. Проверить, не составляя таблиц истинности, какие из высказываний являются тождественно истинными:
1)(p p) p ;
2)(p¬p) p ;
3)¬(p¬p);
4)И p¬p .
1)1, 3;
2)все перечисленные;
3)ни одно из перечисленных;
4)4.
4. Проверить, не составляя таблиц истинности, какие из высказываний являются тождественно ложными:
1)(p p) p ;
2)(p¬p) p ;
3)¬(p¬p);
4)И p¬p .
1)1, 3;
2)все перечисленные;
3)ни одно из перечисленных;
4)4.
5. Известно, что импликация p q истинна, а эквиваленция p ¬q ложна. О значениях эквиваленции ¬p q и импликации q p можно сказать:
1)И, И;
2)И, Л;
3)Л, И;
4)Л, Л.
6. Известно, что импликация ¬p q ложна. О значениях конъюнкции p q и дизъюнкции p q можно сказать:
1) И, И;
— 281 —
2)И, Л;
3)Л, И;
4)Л, Л.
7.Известно, что p = И. О значениях высказываний p ¬p и ¬p p можно сказать:
1)И, И;
2)И, Л;
3)Л, И;
4)Л, Л.
8.Известно, что дизъюнкция p q ложна. О значениях высказываний p q и ¬p¬q можно сказать:
1)И, И;
2)И, Л;
3)Л, И;
4)Л, Л.
9. Определить значения высказываний p (q r) и p (q r), если p = И, q = И, r = Л:
1)И, И;
2)И, Л;
3)Л, И;
4)Л, Л.
10.Выяснить, в каких случаях приведенные данные противоре-
чивы:
1)p =И , p q =Л ;
2)p =И , p q =Л ;
3)p =Л , p¬q =И .
1)1, 2;
2)1;
3)2, 3;
4)3.
11. Выяснить, в каких случаях приведенные данные не противоречивы:
— 282 —
1)p =И , p q =Л ;
2)p =И , p q =Л ;
3)p =Л , p¬q =И .
1)1, 2;
2)1;
3)2, 3;
4)3.
12.Указать наборы значений p и q , при каждом из которых выполняется логическое тождество p q ≡¬p q :
1)И, И и Л, И;
2)Л, И и И, Л;
3)И, Л и Л, Л;
4)И, И и Л, Л.
13.Указать наборы значений p и q , при каждом из которых не выполнено соотношение p q ≡q p :
1)И, И и Л, И;
2)Л, И и И, Л;
3)И, Л и Л, Л;
4)И, И и Л, Л.
14. Упростить формулу (p p)¬p :
1)p¬p ;
2)p¬p ;
3)p ;
4)¬p .
15.Упростить формулу ¬p q p :
1) p q ;
2) p q ;
3) p q ;
4) q p .
16.Упростить формулу (¬p q) (¬p¬q):
— 283 —
1)q ;
2)p q ;
3)¬p ;
4)¬p q .
17. Определите, который из четырех студентов сдал экзамен, если известно:
1)если первый сдал, то и второй сдал;
2)если второй сдал, то третий сдал, или первый не сдал;
3)если четвертый не сдал, то первый сдал, а третий не сдал;
4)если четвертый сдал, то и первый сдал.
1)первый и второй сдали;
2)первый, второй и третий сдали;
3)все студенты сдали экзамен;
4)сдал только четвертый.
18. Установить, какие из высказываний истинны, если область определения предикатов совпадает с :
1)( x)[x+5=x−2];
2)( x) x2 +x+1=0 ;
3)( x) −x2 +x−4<0 .
1)1 и 2;
2)3;
3)1 и 3;
4)1, 2 и 3.
19. Установить, какие из высказываний истинны, если область определения предикатов совпадает с :
1)( x) x2 −x+2≥0 ;
2)( x) x2 −5x+6≥0 x2 −2x +1>0 ;
3)( x)[x+4=0].
1)1 и 3;
2)2 и 3;
— 284 —
3)1, 2 и 3;
4)1 и 2.
20. На множестве M ={1,2,3,...,25} заданы предикаты: P(x) — «x — нечетное число» и Q(x) — «x — кратно 3». Определить область истинности предиката P(x)Q(x):
1){3,6,9,12,15,18,21,24};
2){6,12,18,24};
3){6,15,24};
4){3,9,15,21}.
3.Основы теории вероятностей
1.Сколькими способами могут разместиться на скамейке:
1)6 человек;
2)5 человек?
1)36 и 25;
2)120 и 95;
3)720 и 120;
4)6 и 5.
2.Двух человек на две должности из 15 кандидатов можно выбрать _______ способами:
1)210;
2)105;
3)7;
4)2100.
3.Спортсмен стреляет по мишени, разделенной на 4 сектора. Вероятности попадания в каждый сектор с первого по четвертый соответственно равны 0,2, 0,3, 0,4 и 0,1. Вероятность, что спортсмен попадет в первый или в четвертый сектор, если сделан один выстрел:
1)0,02;
2)0,2;
3)0,1;
—285 —
4) 0,3.
4. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго — 0,7. Вероятность, что после первого залпа в мишень не попадет ни один из стрелков:
1)
1,3;
2)
0,12;
3)
0,42;
4)
0,88.
5. Три стрелка стреляют по мишени. Вероятность попадания в мишень для первого из них равна 0,7, для второго — 0,5 и для третьего — 0,8. Вероятность, что после первого залпа в мишень попадут 2 стрелка:
1) 0,35;
2) 0,56;
3) 0,47;
4) 0,4.
6. В урне находится 6 белых и 4 красных шара. Из нее последовательно извлекаются 3 шара. Вероятность, что все три шара красные:
1)0,066…;
2)0,5;
3)0,033…;
4)0,75.
7.На каждые 50 лотерейных билетов имеется 5 выигрышных. Некто, купив 3 билета, собирается выиграть хотя бы по одному. Вероятность этого события:
1)0,271;
2)0,1;
3)0,3;
4)0,6.
8.Из колоды в 36 карт наугад выбирают 3 карты. Вероятность, что среди них окажутся два короля:
1)≈0,056 ;
2)0,027;
3)≈0,083 ;
—286 —
4) 0,05.
9. Вероятность того, что наудачу взятое двузначное число окажется кратным 2, или 7, или тому и другому одновременно:
1)≈0,144 ;
2)≈0,567 ;
3)≈0,644 ;
4)≈0,078 .
10.Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 =0,75 , p2 =0,8 , p3 =0,85 . Вероятность хотя бы од-
ного попадания при одном залпе из всех этих орудий:
1)0,35;
2)0,45 ;
3)0,825 ;
4)0,925 .
11. Слово «папаха» составлено из букв разрезной азбуки. Карточки с буквами перемешивают, вытаскивают по очереди и раскладывают в ряд. Вероятность получить на первых четырех карточках слово «папа»:
1)≈0,65 ;
2)≈0,033 ;
3)≈0,066 ;
4)≈0,66 .
12. В каждом из трех ящиков находится по 30 деталей. В первом ящике — 27, во втором — 28, в третьем — 25 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Вероятность, что все три вынутые детали окажутся стандартными:
1)0,7 ;
2)0,8 ;
3)0,6 ;
4)0,9 .
— 287 —
13. На фабрике, изготовляющей болты, первая машина производит 30%, вторая — 25%, третья — 45% всех изделий. Брак в их продукции составляет соответственно 2%, 1%, 3%. Вероятность того, что случайно выбранный болт окажется дефектным:
1)0,011;
2)0,033 ;
3)0,022 ;
4)0,044 .
14. Электрическая лампочка может принадлежать к одной из трех партий с вероятностями 0,2, 0,3 и 0,5. Вероятность того, что лампочка проработает заданное число часов, для этих партий соответственно равна 0,9, 0,8 и 0,7. Вероятность того, что лампочка проработает заданное число часов:
1)0,66 ;
2)0,77 ;
3)0,88 ;
4)0,99 .
15. Имеются три урны с шарами. В первой находится 5 синих и 3 красных шара, во второй — 4 синих и 4 красных, в третьей — 8 синих. Наугад выбирается одна из урн и из нее наугад извлекается шар. Вероятность, что он окажется красным:
1)0,292 ;
2)0,512 ;
3)0,153 ;
4)0,495 .
16.Рабочий обслуживает четыре однотипных станка. Вероятность того, что любой станок в течение часа из-за неполадок потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станках возникают независимо, определить вероятность того, что внимания рабочего в течение часа потребуют все четыре станка:
1)≈0,13 ;
2)≈0,41;
—288 —
3)≈0,97 ;
4)≈0,026 .
17. Трижды подбрасывается игральный кубик. Вероятность, что шестерка выпадет не менее двух раз:
1)≈0,005 ;
2)≈0,008 ;
3)≈0,074 ;
4)≈0,069 .
18. Некоторое изделие выпускается двумя заводами. При этом объем продукции второго завода в 3 раза превосходит объем продукции первого. Доля брака у первого завода составляет 2%, у второго — 1%. Изделия, выпущенные заводами за одинаковый промежуток времени, перемешали и отправили в продажу. Вероятность того, что приобретено изделие со второго завода, если оно оказалось испорченным:
1)0,67 ;
2)0,6 ;
3)0,4 ;
4)0,5 .
19. В прямоугольник с вершинами A(−1;0) , B(−1;5) , C(2;5) , D(2;0) брошена точка. Вероятность того, что ее координаты
(x; y) будут удовлетворять неравенству x2 +1≤ y ≤x+3 :
1) 1;
2) 0,5;
3) 0,7;
4) 0,3.
20. На отрезок единичной длины бросают наудачу две точки. Они разбивают отрезок на три части. Вероятность того, что из этих отрезков можно построить треугольник:
1) 0,5;
2) 0,75;
3) 0,25;
4) 1.
— 289 —
4. Основы теории отношений
1. Выписать элементы декартова произведения A B , если
A={−1;1}, B ={0;1}:
1){−1;0;1};
2){{−1;0},{−1;1},{1;0},{1;1}};
3){−1;0;1;2};
4){(−1;0),(−1;1),(1;0),(1;1)}.
2. Область определения отношения {(x; y) R2 : x+ y2 =0}:
1)R ;
2)(−∞;0];
3)(−∞;0);
4)[0;+∞).
3. Множество значений отношения {(x; y) R2 : x + y =3}:
1)(−∞;3];
2)R ;
3)[3;+∞);
4)[−3;3].
4.Является ли отношение толерантности частным случаем отношения эквивалентности или наоборот:
1)да, отношение толерантности — частный случай отношения
эквивалентности;
2)нет, наоборот, отношение эквивалентности — частный случай отношения толерантности;
3)ни то ни другое, эти отношения совершенно разные и не связаны друг с другом;
4)эти отношения связаны только свойством симметричности и ничем более.
—290 —
5. Является ли отношения «больше либо равно» и «быть родственником» симметричными:
1)да, да;
2)да, нет;
3)нет, да;
4)нет, нет.
6.Является ли отношение «быть квадратом» отношением эквивалентности и, если нет, какие свойства эквивалентности не выполняются:
1)да, является;
2)не является, не выполнено только свойство рефлексивности;
3)не является, не выполнены свойства рефлексивности и симметричности;
4)не является, не выполнены все три свойства — рефлексивности, симметричности и транзитивности.
7.Дано множество M ={1;3;5;6}. Составить матрицу отношения «отличаться на 2»:
1 3 5 6
1
3
5
6
1 0 1 0 0
1
0
1
0
0
1)
2)
3 1 0 1 0 ;
3 1 0 1 0 ;
5 0 1 0 0
5
0
1
0
1
6 0 0 0 0
6
0
0
1
0
1
3
5
6
1
3
5
6
1
0
1
1
0
1
0
1
0
0
3)
1
0
1
4)
3
0 ;
3 0 0 1 0 .
5
0
1
1
1
5
0
0
0
0
6
0
0
1
0
6
0
0
0
0
— 291 —
8. Матрица антирефлексивного отношения обладает следующим свойством:
1) главная диагональ матрицы содержит только нули;
2) главная диагональ матрицы содержит только единицы;
3) матрица симметрична относительно главной диагонали, на главной диагонали могут быть нули и единицы;
4) в матрице отсутствуют единицы, симметричные относительно главной диагонали.
9. Матрица симметричного отношения обладает свойством:
1) главная диагональ матрицы содержит только нули;
2) главная диагональ матрицы содержит только единицы;
3) матрица симметрична относительно главной диагонали, на главной диагонали могут быть нули и единицы;
4) в матрице отсутствуют единицы, симметричные относительно главной диагонали.
10. Матрица антисимметричного отношения обладает свойством:
1)главная диагональ матрицы содержит только нули;
2)главная диагональ матрицы содержит только единицы;
3)матрица симметрична относительно главной диагонали, на главной диагонали могут быть нули и единицы;
4)в матрице отсутствуют единицы, симметричные относительно главной диагонали.
11.Матрица рефлексивного отношения обладает свойством:
1)главная диагональ матрицы содержит только нули;
2)главная диагональ матрицы содержит только единицы;
3)матрица симметрична относительно главной диагонали, на главной диагонали могут быть нули и единицы;
4)в матрице отсутствуют единицы, симметричные относительно главной диагонали.
12.Тип отношения «предшествования букв» русского алфа-
вита:
1)отношение частичного порядка;
2)отношение толерантности;
— 292 —
3)отношение совершенно строгого порядка;
4)отношение эквивалентности.
13. Найти матрицу отношения A B , если известны матрицы
отношений
1
0
1
1
A=
и B =
:
0
0
0
0
1 0 1) ;
0 0
1 1 2) ;
0 0
0 1 3) ;
1 0
0 0 4) .
1 1
14. Найти матрицу отношения A∩B , если известны матрицы
1
0
1
1
отношений A=
и B =
:
0
1
0
0
1)
1
0
;
0
0
2)
1
1
;
0
0
3)
0
1
;
1
0
4)
0
0
.
1
1
15. Найти матрицу отношения AB , если известны матрицы
1
0
1
1
отношений A=
и B =
:
0
1
0
1
— 293 —
1 0 1) ;
0 1
1 1 2) ;
1 0
0 0 3) ;
0 1
1 1 4) .
0 1
16. Дано A={1;0}, B ={−1;3} и f (x)=x3 . f (A B):
1){−1;1;2;4};
2){−1;1;0;27};
3){1;4;16};
4){1;1;4;16}.
17. Дано A={1;2}, B ={1;4} и f (x)=x2 . f (A∩B):
1);
2){1};
3){1;4};
4){1;4;16}.
18. Отношение A задано на трехэлементном множестве
1
0
1
1
матрицей 0
0 . Матрица обратного отношения:
0
1
1
1
0
1
1
0
1
1)
2)
0 1 0 ;
0 0
0 ;
0
0
1
1
1
1
— 294 —
0
0
1
1
0
0
3)
4)
0 1
0 ;
0 1
0 .
0
0
1
0
0
1
19. Составить матрицу, задающую отношение «больше, либо равно» на множестве M ={1;2;3}:
1
0
0
1
0
0
1)
2)
0 1 0 ;
1 1
0 ;
0
1
0
1
1
1
0
0
0
0
0
1
3)
4)
1 0 0 ;
0 1 0 .
1
0
1
0
1
0
20. Тип отношения «равновеликость» на множестве плоских треугольников:
1)отношение совершенно строгого порядка;
2)отношение строгого порядка;
3)отношение эквивалентности;
4)отношение частичного порядка.
— 295 —
áДСДзаь Сгь дйзнкйгъзхп кДЕйн
Варианты контрольной работы выбираются по начальной букве фамилии студента.
Начальные буквы фамилии студента
Номер варианта
А, Е, Ё, Л, М, Р, Ч
1
Б, Н, П, Т, Ш, Я
2
В, Ж, И, У, Щ
3
Г, З, О, Ф, Э, Ю
4
Д, К, С, Х, Ц
5
Работа должна быть выполнена в печатном виде на компьютере. Задачи записываются с условиями и объяснениями основных этапов и методов решения. Набор математических формул (включая матрицы) осуществляется в Microsoft Equation (входит в состав Microsoft Office) либо в Math Type. Графики строятся в любой программе символьных вычислений или в Excel’е. Построение гра-
фиков «от руки» не допускается. Отсканированные копии «руко-
пашного» текста проверяться не будут. Примеры оформления решений приводятся в разделе «Практикум».
Вариант № 1
1.
Найти произведение матриц
A и B−1 , если
1
2
A=
,
0
3
1
−1
B =
.
1
1
2. Построить график отношения 2x2 +3y2 =6 . Найти область определения и множество значений.
4.Найти матрицу, задающую отношение «быть квадратом» на множестве M ={1;2;4}.
5.Вероятность попадания в мишень для первого стрелка равна 0,8, а для второго — 0,7. Найти вероятность, что после первого залпа мишень не будет поражена.
Вариант № 2
1.Найти симметрическую разность множеств A и B , если
A={π;e;1;2;3} и B ={−π;e;−1;2;3}.
2.Преобразовать логическую формулу так, чтобы знак отрицания относился только к отдельным переменным ¬(¬pq p¬q).
3.Пусть B — отношение «быть братом», C — отношение «быть родственником». Описать отношения B C и B ∩C .
1
0
1
4. Найти обратную матрицу для
1
A= 0
2 .
0
0
3
5. Из стандартной колоды карт вынимаются две карты без возвращения. Какова вероятность, что обе карты черной масти?
Вариант № 3
1. Проверить, являются ли матрицы
3
5
и
5
3
A=
B =
1
2
2
1
перестановочными.
2. Определите тип геометрического отношения подобия.
3. Найдите логические значения переменных в формуле ¬(p q) q , если известно, что значение формулы — ложь.
— 297 —
4. Как можно определить пересечение множеств: а) прямоугольных треугольников и равнобедренных треугольников; б) прямоугольных треугольников и равносторонних треугольников.
5. В корзине 7 белых и 13 красных шаров. Наудачу извлекаются два шара (без возвращения). Какова вероятность, что оба шара белые?
Вариант № 4
1.
Выяснить,
тождественна ли
формула U −(A B)=
=(U −A)∩(U −B) . Продемонстрировать с помощью диаграмм.
2.
Вычислить
определитель
произведения
матриц
3 0
1
1 −1 0
1
A= 0 0
2
и B = 0
1 .
2
2
4
1
0
3
3.Найти область определения и область значений отношения
x+3 y =2 . Нарисовать график.
4.Составить таблицу истинности для логической формулы pqs ¬p qs .
5.Пусть A и B — два произвольных события. Найти выражения для событий, состоящих в том, что:
а) одно из событий не произошло; б) ни одно из событий не произошло.
Вариант № 5
1. Даны множества A=(4;5] и B =(−3;4]. Верно ли, что объединением этих множеств является отрезок?
— 298 —
2. Найти произведения AB и A−1B−1 ,
если
1
9
A=
−5
6
и
1
0
этих
произведений
B =
. Верно ли, что определители
−1
1
равны?
3.Доказать равносильность формулы ¬p (q s) ≡¬pq s путем преобразований.
4.Задать матрицу отношения «быть меньше» на множестве
M ={0;2;4;6;8}.
5.Собрание выбирает председателя и заместителя. Сколькими способами это можно сделать, если в выборах участвует 20 человек?
— 299 —
Çйикйлх д бДуЦнм (щдбДеЦзм)
1.Понятие множества.
2.Операции над множествами, диаграммы Венна.
3.Примеры задач, которые решаются с применением теории множеств.
4.Предложения и высказывания.
5.Виды высказываний.
6.Логические операции: отрицание, конъюнкция и дизъюнк-
A 
B
B
