заочникам / диф ур / Lectures - 3

n

x

Решение: поскольку

e e0,5

и e x

, то

n 0 n!

1 0,5 0,5 2

0,5 3

... 0,5 n

r x . Нужно подобрать

e

2!

3!

n!

n

число n так, чтобы

r x

f

n 1 c

x x

n

ec

0,5 0

n

ec

0,01,

0

n

n 1 !

n 1 !

2n n 1 !

где c 0;0,5 . Поскольку функция

y e x

возрастающая, то

ec

e0,5

e

4

и будем подбирать n из

2n n 1 !

2n n 1 !

2n n 1 !

2n n 1 !

4

0,01 .

неравенства

2n n 1 !

При

n 4 получим

4

1

0,01 ,

значит,

24 4 1 !

4 120

1 0,5 0,5 2

0,5 3

0,5 4 с заданной точностью

e

2

6

24

e 1,5 0,125 0,02083 0,0026 1,65

Пример 2: Вычислить

sin 0,1с точностью 0,000001

Решение: sin x x 31! x3 51! x5 ...

sin 0,1 0,1 31! 0,1 3 51! 0,1 5 ...

Заметим, что в знакочередующемся ряду остаток ряда по модулю не

превосходит его первого слагаемого (этот факт отмечался в доказательстве

признака Лейбница сходимости рядов).

	1		0,1 5		1							1	0,000001, поэтому
	5!				120 105					12000000
	sin 0,1 0,1					1		0,1 3				0,1 0,00017 0,09983
					3!

		x
Пример 3: вычислить интеграл	0,1	sin x	с точностью 0,001.
	0

93

Решение: Поскольку sin x x																		1	x3		1		x5		... , то
																		3!			5!
	sin x		1				1	x 2				1		x4			...
		x					3!				5!
0,1sin x						0,1					x2					x4						x3				x5			0,1
	0 x						1				3!					5!	... dx x					18				600	...
						0																							0
0,1					0,1 3					0,1 5						...
				18							600

В этом знакочередующемся ряду уже второе слагаемое по модулю меньше,

0,1sin x

чем 0,001, поэтому 0,1

0 x

Контрольные вопросы:

1.Что называется формулой Тейлора для заданной функции? Почему формулу Тейлора можно использовать для приближенных вычислений? Покажите, что формула приближенных вычислений с помощью дифференциала (первый семестр) является частным случаем формулы Тейлора.

2.Что называется рядом Тейлора для заданной функции? При каких условиях ряд Тейлора не существует?

3.Запишите как выглядят ряды Тейлора для экспоненты, синуса, косинуса, логарифмической и степенной функций.

4.Что называется остатком ряда Тейлора в форме Лагранжа? Как можно использовать этот остаток для приближенных вычислений с заданной точностью?

Задачи для самостоятельного решения:

1.Доказать, что промежутком сходимости рядов Маклорена для синуса и косинуса является вся числовая прямая.

2.	Доказать, что промежутком сходимости ряда Маклорена для функции	y 1 x
является 1; 1 .
3.	Доказать формулу Эйлера eix cos x i sin x формальным	разложением

участвующих в ней функций в ряды Маклорена.

Лекция 11(45) Ряды Фурье

Ряд Тейлора позволяет свести вычисления значений функций к вычислению значений многочленов. Однако, чтобы для функции существовал ряд Тейлора, необходимо наличие у нее производных любых порядков. Поэтому

даже такая простая функция как y x не имеет ряда Маклорена. В этой

лекции будут рассмотрены представления в виде функциональных рядов функций, для которых не требуется существование производных.

94

Постановка задачи: Дана некоторая функция y x , требуется: 1) Определить, при каких условиях возможно равенство

a0

x

an cos nx bn sin nx ,

где a0 , an , bn - некоторые

2

n 1

действительные числа

2)

При выполнении

первого

условия

найти значения

коэффициентов

a0 , an , bn .

Коэффициенты ряда Фурье12 на симметричном промежутке

a0

Определение: Если x

an cos nx bn sin nx , для любых

2

n 1

x a;b , то

a0

значений переменной

ряд

an cos nx bn sin nx

2

n 1

называется рядом Фурье функции x на промежутке a;b .

Пусть функция x интегрируема на промежутке

; и при

некоторых

значениях

коэффициентов a0 , an , bn имеет

место равенство

a0

x

an cos nx bn sin nx .

2

n 1

; :

Проинтегрируем обе части этого равенства на промежутке

x dx

a0

dx

an

cos nxdx bn sin nxdx

2

n 1

n 1

a0

dx

a0

x

a0

2 a

0

2

2

2

1

cos nxdx

sin nx

0 0 0

n

1

1

cos n cos n 0 ,

sin nxdx

cos nx

n

n

12 Фурье Жан Батист Жозеф (1768-1830) французский математик. Труды по алгебре, дифференциальным уравнениям, математической физике.

95

значит, x dx a0 , откуда находим значение коэффициента a0 :

a0 1

Для нахождения значений

x dx .

коэффициентов an умножим равенство

		a0
	x		an cos nx bn sin nx на				cos mx и проинтегрируем на
	2		n 1	; .
	том же промежутке
	x cos mxdx				a0	cos mxdx an cos nx cos mxdx
					2
						n 1

bn sin nx cos mxdx .

n 1

a0

a0

1

cos mxdx

sin mx

0 0 0

2

2

m

1

sin nx cos mxdx

sin n m x sin n m x dx

2

1

cos n m x

1

cos n

m x

0 , если m n .

n m

n m

Если же m n , то sin n m x 0 ,

1

sin nx cos mxdx

sin n m xdx 0 .

2

cos nx cos mxdx

1 sin n m x n m

		1		cos n m x cos n m x dx
	2
				1		sin n m x
								0 , если m n .
					n m

96

Если m n , то

1

1

cos nx cos mxdx

cos n m x 1 dx 0

dx .

2

2

Значит, x cos mxdx 0 am 0 , и

1

am

x cos mxdx .

Для нахождения

значений коэффициентов bn

умножим равенство

a0

x

an cos nx bn sin nx на sin mx и проинтегрируем на

2

n 1

том же промежутке.

x sin mxdx

a0

sin mxdx an

cos nx sin mxdx

2

n 1

bn sin nx sin mxdx :

n 1

		a0									a0	1
				sin mxdx										cos mx			0
		2									2		m
						1
	cos nx sin mxdx								sin n m x sin m n x dx 0
					2
					1
	sin nx sin mxdx							cos n m x cos m n x dx 0 , если
					2
	m n .
															1
	Если m n , то			sin nx sin mxdx												1 cos m n x dx 0 , и
												2
	x sin mxdx bm , значит,
								1
				bm						x sin mxdx

97

Итак, если на промежутке ; справедливо равенство

a0

x

an cos nx bn sin nx , то

2

n 1

1

a0

x dx

1

am

x cos mxdx

1

bm

x sin mxdx

Замечание: пусть

функция

y x

интегрируема

на произвольном

симметричном промежутке l;l , тогда,

сделав замену

x

lt

, получим

lt

интегрируемую на промежутке ; . Значит, имеет

функцию

,

смысл рассматривать равенство lt

Возвращаясь к переменной x , получим

	a0
		an cos nt bn sin nt .
	2
		n 1

x

a0

nx

nx

an cos

bn

sin

и при этом

2

l

n 1

l

a

1

l x dx

0

l

l

a

1

l x cos mx dx

m

l

l

l

b

1 l

x sin

mx dx

l

m

l

l

y x на промежутке ; .

Пример: Найти ряд Фурье для функции

1

x

2

2

2

Решение: a0

xdx

0

98

1

1

x

1

a

x cos mxdx

sin mx

sin mxdx

m

m

m

1

1

0 0

cos mx

0 ,

m2

1

1

x

1

b

x sin mxdx

cos mx

cos mxdx

m

m

m

1

1

2

m cos m m cos m m2

sin mx

m cos m .

cos n

cos n 1, а

Значит, x 2

sin nx . Поскольку,

при четных n

n

n 1

n

n

при нечетных cos n 1,

то можно записать x 2

1

sin nx .

k 1

Замечание: при нахождении ряда Фурье для нечетной функции y x

получили, что под знаком суммы нет косинусов (четных функций) и

	присутствуют только синусы (нечетные функции). Это не случайно. Можно
	доказать, что если функция	y x				нечетная, то ее ряд Фурье на
	промежутке ; имеет вид
	x
		bn sin nx ,
			n 1
	а если четная, то
	x		a0
					an cos nx .
		2			n 1

Условия возможности разложения функции в ряд Фурье

В предыдущей части лекции были вычислены коэффициенты ряда Фурье в предположении, что такой ряд для данной функции существует. Сейчас сформулируем теоремы, в которых будут даны достаточные условия существования такого ряда и условия его сходимости именно к рассматриваемой функции.

99

Определение: Говорят, что функция y x удовлетворяет на интервалеa;b условию Гѐльдера, если существуют числа L R и 0;1 такие, что для любых точек x1 , x2 a;b выполняется неравенство

x

x

2

L

x x

2

1

1

Замечание: Можно доказать, что если функция имеет на промежутке a;b

непрерывную производную, то она удовлетворяет условию Гѐльдера.

Теорема (о разложении в ряд Фурье)

Если

функция y x

удовлетворяет условию Гѐльдера на промежутке l;l , то

x

a0

nx

nx

an

cos

bn sin

2

l

l

n 1

Без доказательства.

Теорема (признак Дирихле) Если функция

y x кусочно-монотонна

на промежутке l;l и имеет на этом промежутке не более, чем конечное

число точек разрыва, то ее ряд Фурье сходится к значению функции в
каждой точке непрерывности и к числу
	lim x	lim x
	x x0 0	x x0 0
2

в каждой точке разрыва первого рода x0 .

Без доказательства.

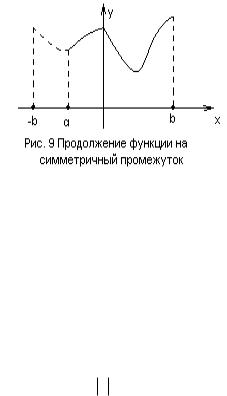
Коэффициенты ряда Фурье на произвольном промежутке

Пусть дана

функция y x на

промежутке

0;l . Продолжим ее

произвольным

образом

на

промежуток

l;0 ,

получим

функцию,

заданную на

симметричном

промежутке

l;l , для

которой

известен

метод нахождения ряда Фурье.

l;l новая функция

Если продолжить функцию так, чтобы на интервале

стала четной,

то можно

разложить

эту

функцию

в

ряд

по косинусам

x

a0

an cos nx . Если же

продолжить

ее

так,

чтобы новая

2

n 1

100

функция стала нечетной, то можно разложить эту функцию в ряд по

синусам x bn sin nx .

n 1

Пример: Разложить функцию y 1 в ряды Фурье по синусам и косинусам на интервале 0; .

Решение: Разложим сначала в ряд по синусам.

				1									1	0									1
bm							y sin mxdx								1 sin mxdx													1 sin mxdx
																											0
			1	0					1								1												0				1
					sin mxdx						sin mxdx								cos mx															cos mx
																m																	m
											0																												0
	1		cos 0 cos m										1		cos m cos 0												2					1 cos m
	m																								m
												m
При			четных					значениях						m 2k , b						2	1 1 0 ;															при			нечетных
															m					m
																																					m 2k 1:
																			bm							2				1 1							4		. Значит,
																																					m
																								m
																																4				sin 2k 1 x .
																			1
																												2k 1
																					k 1

Теперь разложим в ряд по косинусам:

101

1

1

1

2

a0

1 dx

x

1

1

am

1 cos mxdx

sin mx

0

m

1

1

bm

1 sin mxdx

cos mx

0

m

таким образом, ряд Фурье по косинусам функции

y 1 состоит

из

единственного слагаемого

y 1,

или, иными словами эта функция сама

является своим рядом Фурье.

Пусть дана функция y x

на

произвольном

положительном

промежутке a;b . Продолжим ее

произвольным

образом

на

промежуток

0; a ,

получим

функцию,

заданную

на

промежутке

0;b .

Затем

продолжим

эту

функцию

на

промежуток

b;b .

Получим

функцию,

для которой известен

метод нахождения ряда Фурье.

Аналогично можно поступить, если функция задана на

отрицательном

промежутке a;b

: сначала продолжим ее на промежуток

b;0

и получим

функцию на промежутке a;0 , затем продолжим ее на промежуток 0;a И получим функцию на симметричном промежутке a; a . В обоих этих

случаях можно искать ряд Фурье только по синусам или только по косинусам.

Пусть функция y x задана на промежутке a;b , внутри которого расположена точка 0 a 0;b 0 .

Допустим, что a b . Продолжим функцию произвольным образом на промежуток b; a , получим функцию на симметричном промежутке

102