заочникам / диф ур / Lectures - 3

Определение:		если уравнение имеет k одинаковых корней x0 , то говорят,
что корень x0		имеет кратность k.
Пример: Найти все корни многочлена x5 6x4 9x3
Решение: x5 6x4			9x3 x3	x2 5x 6 x x x x 3 x 3
Выражение	x x x x 3 x 3 равно нулю тогда, когда равен нулю
хотя бы один из сомножителей, т.е. x 0 или x 0 или					x 0 или
x 3 0	или		x 3 0 .	Значит, уравнение имеет	5 корней:
x1 x2 x3 0 ,			x4 x5 3.

Приведем без доказательства одну важную формулу (формулу Эйлера2), которая понадобится нам в дальнейшем. Доказательство этой формулы будет приведено в одной из последующих лекций.

eix cos x i sin x для любого действительного числа х.

Контрольные вопросы:

1.Что называется мнимой единицей? Что называется комплексным числом?

2.Каковы правила сложения, вычитания, умножения и деления комплексных чисел?

3.Как возвести комплексное число в целую степень? Как извлекается корень из комплексного числа?

4.Что такое формула Эйлера?

Задачи для самостоятельного решения:
1.	Доказать, что существует ровно n комплексных корней степени	n из комплексного числа.
2.	Доказать, что корни степени n из действительного числа являются вершинами правильного

многоугольника с центром в начале координат.

Лекция 2(36) Дифференциальные уравнения первого порядка

Задачи, приводящие к понятию дифференциального уравнения

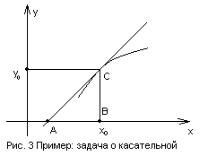
Задача 1. Найти все линии, для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть

величина постоянная, равная 12 a 2 .

2 Эйлер Леонард (1707-1783) математик, механик, физик и астроном. Автор более 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. С 1727 г. работал в России, академик Петербургской академии наук.

13

Решение:					x x		.
Уравнение касательной в точке x	0	имеет вид y y	0	y'		0
				0

Ордината точки А равна нулю, поэтому из уравнения касательной найдем ее

абсциссу: 0 y

y'

x x

;

x x

y0

.

0

0

0

0

y '

0

Длина

катета

ВС равна

y0 ,

а

длина

катета

АВ

равна

разности

абсцисс

y

0

y

0

точек В и А:

x

x

.

0

0

'

'

y0

y0

Площадь прямоугольного треугольника

АВС

равна

половине

произведения

катетов, значит,

y02

a 2 .

Поскольку

y '

0

это соотношение должно быть верно в любой точке линии, то

y 2

a 2 .

y '

Таким образом, для определения уравнения линии получили уравнение, в котором в качестве неизвестных фигурируют функция y и ее производная.

Задача 2. В сосуд, содержащий 10 л. воды, непрерывно поступает со скоростью 2 л. в минуту раствор, в каждом литре которого содержится 0,2 кг. соли. Поступающий в сосуд раствор непрерывно перемешивается с содержимым сосуда, и смесь вытекает оттуда с той же скоростью. Найти закон изменения количества соли в растворе в зависимости от времени.

Решение: Обозначим y(t) - количество соли в сосуде через t минут после начала поступления раствора в сосуд. За одну минуту поступает 2 л.

раствора,	значит, за промежуток времени t (мин) поступает 2t литров.
В этих 2t		литрах содержится 0,2 2t 0,4t кг. соли. За то же время
t из сосуда вытекает			2t литров раствора. В момент времени t в сосуде
содержится		y(t) кг. соли, значит, если бы содержание соли в сосуде не
менялось,	то в 2t		литрах	вытекающего раствора содержалось бы
0,2t y(t)		кг. соли. Поскольку же содержание соли непрерывно
меняется, то в вытекающих 2t				литрах содержится 0,2t y(t) , где

0 при t 0 . Приращение количества соли в растворе за время

14

t равно	y t t y(t) 0,4t 0,2t( y(t) ) .	Полученное
равенство поделим на t и устремим t 0 . Получим уравнение
y' 0,4 0,2 y .
Определение:	Дифференциальным уравнением порядка n	называется

уравнение, связывающее независимую переменную, неизвестную функцию этой независимой переменной и производные этой функции до порядка n включительно.

Понятие о решении дифференциального уравнения

Определение: Решением дифференциального уравнения называется функция, обращающая уравнение в тождество при любых значениях независимой переменной.

Определение: Решению дифференциального уравнения соответствует некоторая линия на координатной плоскости, называемая интегральной кривой этого уравнения.

Пример:

Функция

y

a 2

является решением

дифференциального

x

y

2

a

2

y

2

a

4

a

2

уравнения

a 2 .

Действительно,

y '

и

:

a 2 .

y '

x 2

y '

x2

x 2

Далеко не всегда удается найти решение дифференциального уравнения в виде элементарной функции. Например, чтобы найти решение простейшего

	x		x
уравнения y '	sin x	, нужно найти «неберущийся» интеграл		sin x	dx .

Если можно найти решение дифференциального уравнения в виде композиции элементарных функций и интегралов от элементарных функций (даже заданных неявно или параметрически), то говорят, что уравнение

интегрируется в квадратурах.

y 2

a 2 .

Пример 1: Решить уравнение

y '

Преобразуем уравнение: y '

y 2

;

dy

y 2

;

dx

a 2

;

x'

a 2

.

a 2

dx

a 2

dy

y 2

y 2

15

В последнем уравнении подразумевается, что переменная x является функцией от независимой переменной y . Значит, чтобы найти функцию x ,

достаточно взять неопределенный интеграл: x a 2			dy		a 2	C .
			2		y
			y
y	a 2	.
	x C

Пример 2: Найти все линии на плоскости, имеющие кривизну, равную 0. Кривизна графика функции y x задается формулой

			y ''
				3
		1 y ' 2
					2
Решаем дифференциальное уравнение				y		''				0 :	y'' 0
						3
			1 y ' 2
								2
y' C1 ;	y C1dx C1 x C2 . Как			и			следовало				ожидать, такими

линиями являются только прямые.

Заметим, что в первом примере при решении уравнения первого порядка получили ответ, зависящий от одной произвольной постоянной С1 , а при решении во втором примере уравнения второго порядка получили ответ, зависящий от двух произвольных постоянных С1 ,С2 . В общем случае, как

правило, при решении дифференциального уравнения порядка n решение будет зависеть от n произвольных постоянных.

Дифференциальные уравнения первого порядка

В соответствии с определением, дифференциальное уравнение первого порядка имеет вид F x, y, y' 0 , где x - независимая переменная

y y(x) - неизвестная функция, y'		y' (x) - производная этой функции,
F - заданная функция трех переменных.
Если	дифференциальное уравнение	первого порядка задано в виде
y'	f (x, y) , то оно называется, уравнением, разрешенным относительно

производной.

16

Дифференциальное уравнение первого порядка может быть задано и в виде f (x, y)dx g(x, y)dy 0 , где f (x, y), g(x, y) - заданные функции

двух переменных.

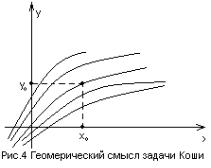
Одной из основных задач теории дифференциальных уравнений является задача Коши: найти решение дифференциального уравнения y' f (x, y) ,

удовлетворяющее	условию
y(x0 ) y0 , где	x0 , y0 - заданные

числа. Геометрически задачу Коши можно интерпретировать так: из множества всех интегральных кривых дифференциального

уравнения y' f (x, y) выбрать ту, которая проходит через заданную

точку M x0 , y0 .

Определение: Множество решений дифференциального уравнения первого порядка, зависящее от одной

произвольной постоянной будем называть общим решением этого уравнения.

y

2

a 2

Пример:

Общим решением

уравнения

является множество

y '

функций

y

a 2

.

x C

Определение:

Если

общее

решение

можно

представить

в виде

С (x, y) ,

т.е. выразить

в нем произвольную постоянную через

переменные

x

и

y , то функция

z (x, y)

называется

общим

интегралом дифференциального уравнения.

Пример:

Из

общего

решения

y

a 2

следует,

что

С x

a 2

,

x C

y

значит,

функция

z x

a2

является

общим

интегралом

y

y 2

a 2 .

дифференциального уравнения

y '

17

Дифференциальные уравнения с разделяющимися переменными

Определение: Уравнение	вида f (x)dx g( y)dy 0	называется
уравнением с разделенными переменными.
Запишем уравнение с	разделенными переменными	в виде

f (x)dx g( y)dy и проанализируем его. В левой и правой частях

уравнения находятся дифференциалы некоторых функций, и они равны. Значит, равны и производные этих функций. По теореме о совпадении производных эти функции могут отличаться друг от друга лишь на

произвольную постоянную: f (x)dx g( y)dy С . Это равенство и есть общее решение уравнения с разделенными переменными.

Определение: Дифференциальные уравнения вида y' f (x)g( y) или вида f1 (x) f2 ( y)dx g1 (x)g2 ( y)dy 0 называются уравнениями с разделяющимися переменными.

Для решения уравнения f1 (x) f2 ( y)dx g1 (x)g2 ( y)dy 0 необходимо поделить его на f2 ( y)g1 (x) и будет получено уравнение с разделенными

	переменными. Тот		же прием применяется при решении уравнения
	y' f (x)g( y) :	dy	f (x)g( y) ,	dy	f (x)dx .
		dx		g( y)

Замечание: При делении могут быть потеряны решения, поэтому после деления на переменную величину необходима проверка.

Пример		1: Найти общее решение дифференциального уравнения
xydx	x 1 dy 0
Решение:		xydx x 1 dy

Добьемся того, чтобы в левой части равенства отсутствовала переменная y , а в правой части – переменная x . Для этого поделим все уравнение на

y x 1 :

	x		dx	dy
	x 1			y

	x 1				y
Возьмем интегралы от обеих частей уравнения:		x	dx		dy	C
							0

18

	x 1 1	dx ln y ln C . Вместо постоянной С для удобства
	x 1

написали постоянную lnC.

1

1 dx ln y ln Cx 1

xln x 1 ln y ln C ; ln ex ln x 1 ln y ln C

e x

C

e x

C

C x 1

ln

ln

;

;

y

.

x 1

e x

y

x 1

y

Пример 2: Решить задачу Коши x2

1 y' 2xy 2 0 ,

y(0) 1

Решение: Найдем общее решение уравнения. x2

1

dy

2xy 2 ,

dx

x2 1 dy 2xy 2 dx ;

dy

2xdx

;

dy

2xdx

C ;

y

2

x

2

1

y

2

x

2

1

1

ln

x2 1

C . Это

равенство можно

считать

общим решением

y

(в виде неявной функции). Поскольку при решении уравнения

производилось деление на переменные величины

y 2

и

x2 1,

то

необходимо поверить, не являются ли функции

y 2

0

и

x2 1 0

решениями дифференциального уравнения. Если

y 2

0 ,

то

y 0

и

y ' 0 . При подстановке в уравнение y 0 и y '

0 получим тождество,

значит, y 0 -

еще одно решение дифференциального уравнения. Если

x2 1 0 , то

x 1 и при

подстановке

этих значений в

уравнение

тождество не получается.

Теперь воспользуемся условием

y(0) 1.

Для

этого в общее решение

вместо переменной x подставим число 0, а вместо

y - число 1:

1

ln

02 1

C

1

Значит, C 1 и это значение подставляем в общее решение:

1y ln x2 1 1

19

y 1 . ln x2 1 1

Линейные уравнения

Определение: дифференциальное уравнение первого порядка называется линейным уравнением, если оно может быть представлено в виде y' p x y q x 0 , где p x , q x - заданные функции.

Метод решения линейного уравнения состоит в следующем: неизвестную

функцию y заменяем	произведением двух неизвестных функций
y u v , тогда y' u' v u v' и уравнение перепишется так:
u'v uv'	p(x)uv q(x)
u'v u v' p(x)v q(x)
Теперь подберем функцию	v так, чтобы v' p(x)v 0 . Это равенство

является дифференциальным уравнением с разделяющимися переменными. Достаточно найти его общее решение и в качестве произвольной

постоянной С взять любое число. Допустим, что v0 - какое-либо решение

дифференциального уравнения v' p(x)v 0 . Подставив это решение в

уравнение u'v u v' p x v q x , получим u'v0 q(x) . Теперь неизвестную функцию u можно найти интегрированием выражения

q(x)

.

v0

Пример: Найти общее решение уравнения y' ytgx cos 1

x .

Решение: Пусть y u v , тогда y'

u' v u v' :

u'v u v' tgxv cos 1

x . Решаем уравнение v' tgxv 0 :

dv

tgxv ;

dv

tgxdx ;

dv

tgxdx ;

dv

sin x

dx ;

v

dx

v

v

cos x

ln v ln cos x .

v cos x . Подставим найденную функцию в уравнение

u' cos x cos 1 x ; u '

1

;

u

dx

tgx C

cos

2

cos

2

x

x

y u v (tgx C) cos x sin x C cos x .

20

Однородные уравнения

Определение: Функция двух переменных z f (x, y) называется однородной функцией порядка n , если для любого значения переменной t выполняется равенство f (tx,ty) t n f (x, y) .

Определение: Функция двух переменных			z f (x, y)	называется
положительно	однородной	функцией порядка	n , если для любого
положительного	значения	переменной t	выполняется	равенство

f (tx,ty) t n f (x, y) .

Замечание: любая однородная функция является положительно однородной, но обратное не верно.

Примеры: 1) Функция			f (x, y) x2 y 2	- однородная функция второго
порядка,	т.к.	f (tx,ty) tx 2 ty 2 t 2			x2 y2 t 2 f (x, y) .
Аналогично,	функции		f (x, y) x3	y3 ,	f (x, y) x2 y y 2 x

являются однородными функциями третьего порядка.

2)Функция f (x, y) x y - однородная функция нулевого порядка, т. к.

xy

f (tx,ty)

tx ty

t x y

x y

t 0 f (x, y)

tx ty

t x y

x y

3) Функция

f (x, y)

x2 y 2 - положительно однородная функция

t

первого порядка,

т.к.

f (tx,ty)

t 2 x2

y 2

x2 y 2 .

При

t 0 f (tx,ty) t

x2 y 2 tf (x, y) .

Определение: Дифференциальное уравнение

f (x, y)dx g(x, y)dy 0

называется

однородным

дифференциальным

уравнением,

если

f (x, y), g(x, y) - однородные функции одного порядка.

Следствие: Дифференциальное	уравнение	y'	f (x, y) является
однородным тогда и только тогда,	когда f (x, y) -		однородная функция
нулевого порядка.

Метод решения однородного дифференциального уравнения состоит в замене неизвестной функции y на произведение y zx , где x -

21

независимая переменная, z - новая неизвестная функция. При этом y' z ' x zx' z ' x z . Можно доказать, что после такой замены

однородное уравнение превратится в уравнение с разделяющимися переменными.

Пример: Найти общее решение уравнения y '

x y

x y

Решение:

z ' x z

x zx

;

z ' x z

1 z

;

dz

x

1 z

z ;

x zx

1 z

dx

1 z

dz

x

1 z z z 2

1 z 2

;

1 z

dz

dx

;

1 z

dz

dx

;

dx

1 z

1 z

2

x

2

x

1 z

1 z

dz

zdz

dx

; arctgz

1

ln 1 z 2 ln x C .

1

2

2

x

z

1 z

2

y

y

1

y

2

z

ln 1

Делаем обратную замену

: arctg

ln x C .

x

x

2

x

Общее решение получено в виде неявной функции.

Контрольные вопросы:

1.Что называется дифференциальным уравнением? Что такое «интегрируемость в квадратурах»?

2.Что называется задачей Коши? Какова последовательность решения задачи Коши? В чем геометрический смысл задачи Коши?

3.Каков метод решения уравнения с разделяющимися переменными?

4.Что называется линейным дифференциальным уравнением первого порядка? Каков метод решения линейного уравнения?

5.Что называется однородным уравнением? Каков метод решения однородного уравнения?

Задачи для самостоятельного решения:

1. Доказать, что уравнение Бернулли y' p(x) y q(x) y 0 , где - действительное

число, после умножения на			1 y	и	замены y1	z	становится		линейным
уравнением относительно функции z .
2.	Доказать,	что после замены y zx однородное уравнение превратится в уравнение с
разделяющимися переменными.
3.	Найти	метод решения	дифференциального уравнения			y '	ax by c				, где
							f
							gx hy		k
a,b, c, g, h, k - действительные постоянные,				f	- некоторая функция.

22