заочникам / диф ур / Lectures - 3

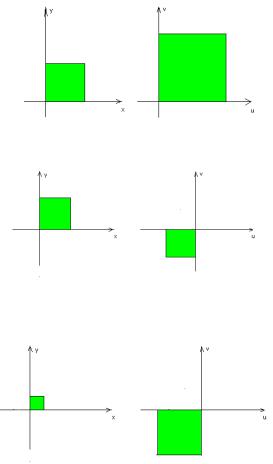
Если 0 - действительное число, то функция	w z при 1
осуществляет растяжение плоскости в раз, а при	0;1 - сжатие.

Действительно, если z cos i sin и cos 0 i sin 0 , тоz cos 0 i sin 0 cos i sin .

Рис. 30 Растяжение (сжатие) плоскости

Отображение w z сопоставляет каждому вектору противоположный,

Рис. 31 Поворот

поэтому, при 0 отображение w z будет являться композицией поворота на 180 и сжатия или растяжения.

Рис. 32 Поворот с растяжением

143

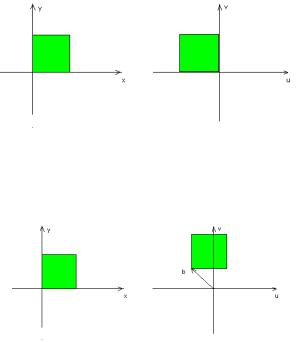
Рассмотрим отображение	w iz . Поскольку		i 1					i sin			и
						cos
							2			2
z cos i sin , то											и
	w iz cos					i sin				,
				2					2
отображение w iz осуществляет поворот на			90 .

Рис. 33 Поворот (2)

Следовательно, отображение w az при любом комплексном a является композицией какого-либо поворота и растяжения (сжатия).

Функция w z b , очевидно, осуществляет параллельный перенос на вектор b .

Рис. 34 Параллельный перенос

Следовательно, линейная функция является композицией поворота, растяжения (сжатия) и параллельного переноса.

Дробнолинейное отображение

	Определение: функция w	az b	, где a, b, c, d	- комплексные числа,
		cz d
	удовлетворяющие соотношению		ad bc 0 ,	называется дробно-
	линейной.

144

	Замечание:	при условии ad bc 0 из	равенства w	az b	можно
				cz d
	однозначно	выразить переменную z через	w , значит, дробно-линейная

функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя.

Рассмотрим

отображение

w

1

(назовем

его

обратной

z

пропорциональностью):

1

1

cos i sin

1

cos i sin .

z

cos i sin

cos 2 sin 2

Если

1 ,

то точка комплексной плоскости при этом отображении

переходит в точку, симметричную ей относительно оси абсцисс.

При

1 , то кроме симметричного отображения происходит сжатие, а

при

1

- растяжение.

При этом

внутренность

круга

как бы

«выворачивается» наружу и при этом точка 0 переходит в точку , а точка- в точку 0.

Рис. 35 Отображение

1

w z

с 0 (в

Будем

считать,

что

противном

случае

получим

линейную

функцию), тогда

az b

a z ba 1

a z dc 1 ba 1 dc 1

w

cz d c

z dc 1 c

z dc 1

a

ba

1

dc

1

a

1

bc ad

a

bc ad

1

c

1

z dc

1

c

1

ac

z dc

1

c

c

2

z

dc

1

Рассмотрим отображения: w

z dc 1 (параллельный перенос)

1

w

1

(обратная пропорциональность)

2

w1

145

w3 bc ad w2 (поворот с растяжением) c 2

w ac w3 (параллельный перенос)

Таким образом, дробно-линейное отображение является композицией обратной пропорциональности, параллельных переносов, поворота и растяжения (сжатия).

При отображениях параллельного переноса, растяжения (сжатия) и поворота любая окружность перейдет в некоторую окружность. Если окружность не проходит через начало координат, то при отображении

w 1z она также перейдет в окружность. Если же окружность проходит

через начало координат, то при отображении w 1z она перейдет в прямую.

Если считать прямую окружностью бесконечно большого радиуса, то при дробно-линейном отображении любая окружность перейдет в окружность.

Поскольку

z z0

x iy x0

iy0 x x0 i y y0 ,

то

z z

0

x x

0

2

y y

0

2

и поэтому равенство

z z

0

R

можно рассматривать как уравнение окружности с центром в точке			z0
радиуса R .
		1
Пример 1: найти область, в которую переходит круг	z 1		при

отображении w 1z .

Решение: Сначала найдем, в какую линию перейдет окружность z 1 1.

Рис. 36 Пример дробно-линейного отображения

146

Поскольку окружность проходит через начало координат, то ее образом будет прямая (т.к. точка 0 перейдет в точку ). Точка 2, лежащая на

окружности		z 1		1, перейдет в точку										1	, а точка 1 i , также лежащая на
								1 i				2
окружности – в точку						1				1		1	i .
						i
1								2		2		2

	Рис. 37 Пример дробно-линейного отображения (2)
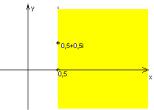
Значит,	окружность		z 1		1 переходит в вертикальную прямую			x 0,5 .
							1 перейдет сама
Точка	1, лежащая		внутри круга			z 1		в себя,

следовательно внутренность круга перейдет в полуплоскость, расположенную правее прямой x 0,5

Контрольные вопросы:

1.Что называется комплексной экспоненциальной функцией? Каковы ее свойства? Что является областью однолистности экспоненциальной функции?

2.Что называется комплексным синусом и комплексным косинусом? Каковы свойства этих функций? Что называется комплексным тангенсом и комплексным котангенсом?

3.Что называется степенной функцией, какова область ее однолистности? Что называется комплексным логарифмом? Какова связь обратных тригонометрических функций с комплексным логарифмом?

4.Что называется линейной функцией? Композицией каких простейших отображений является линейная функция? Что называется дробнолинейной функцией? Композицией каких простейших отображений является дробно-линейная функция?

Лекция 17(51) Дифференцирование и интегрирование функций комплексной переменной

Формулы Коши-Римана

Пусть в области D задана функция комплексной переменной w f z u x, y iv x, y .

147

Определение: Пусть точки z и z z принадлежат области		D , тогда
величина w f z z f z u x, y i v x, y		называется
приращением функции w .
Определение: Если существует конечный предел
f ' z lim	w ,
z 0	z

то он называется производной функции w по переменной z . Определение: Функция f z u x, y iv x, y , имеющая производную в точке z D , называется моногенной в этой точке.

Теорема (о непрерывности функции, имеющей производную)

Если функция моногенна в точке z D , то она непрерывна в этой точке.

Без доказательства.

Придадим приращение только переменной x , оставляя

y фиксированным:

z z x x iy , тогда

'

f x iy x

f x iy

f

z lim

x

x 0

u x x, y

u x, y

i

v x x, y

v x, y

u

i

v

lim

x

x

x

x

x 0

Теперь придадим приращение только переменной y , оставляя x

фиксированным: z z x i y y .

f x iy i y

f x iy

f '

z lim

i y

y 0

u x, y y

u x, y

v x, y y

v x, y

lim

i

i y

i y

y 0

i

u

v

.

y

y

Следовательно, u i v i

u

v . Отсюда следуют формулы Коши-

x

x

y

y

Римана:

148

u

v

x

y

v

u .

x

y

Формулы Коши-Римана являются условиями,

необходимыми

для

моногенности функции w f

z

в точке z .

Замечание: поскольку

z x iy

и z x iy , то из этих двух равенств

можно получить

x

1

z z и

y

1

z z ,

значит, можно считать,

2

2i

что w u z, z iv z, z .

w

w x

w y

1 w

1 w

1

w

w

Поскольку

i

и

z

x z

y z

2 x

2i y

2

x

y

w

w x

w y

1 w

1 w

1

w

w

i

, и,

z

x z

y z

2 x

2i y

2

x

y

кроме того, при выводе формул Коши-Римана предполагалось, что функция w f z не зависит от переменной z , то условия Коши-Римана можно переписать в комплексной форме:

w 0 .z

Теорема (достаточное условие моногенности)

Для моногенности функции w f z u x, y iv x, y в точке z достаточно выполнения формул Коши-Римана и существования полных дифференциалов функций u x, y и v x, y .

Без доказательства.

Определение: Функция w f z называется аналитической в области D , если она моногенна в каждой точке этой области.

По аналогии с функциями действительной переменной имеют место следующие теоремы:

Теорема (производная и аналитические операции)

Если функции f z и g z моногенны в точке z , то:

149

1)f z g z ' f ' z g ' z

2)f z g z ' f ' z g ' z

3) f z g z ' f ' z g z f z g ' z

f z '

f ' z g z f

z g ' z

при условии g z 0

4)

2

g

z

g z

Без доказательства.

Теорема (производная композиции функций)

Если

аналитическая

функция w f

z отображает

область D

расширенной

комплексной плоскости z

на область D '

расширенной

комплексной плоскости w , а функция g w аналитична в области D ' ,

то композиция функций g f z аналитична в области D и

'

g ' f z f ' z

Без доказательства.

Кроме того, можно доказать, что остается верной таблица производных

Комплексное интегрирование

Пусть на комплексной плоскости задана линия L с концами А и В и пусть

в каждой точке этой линии задана непрерывная функция
	f z u x, y			iv x, y .
Поделим линию L точками
A z0 x0	iy0 , z1	x1 iy1 , z2		x2 iy2 ,..., zn xn iyn B ,
на каждой дуге zk zk 1		произвольно выберем по точке k			k i k и
составим сумму
		n 1	k	zk 1 zk .
		f
		k 0
Обозначим	zk 1 zk zk ,		xk 1 xk xk ,		yk 1 yk yk ,
u k ,k uk , v k ,k vk , тогда
n 1		n 1
f k zk 1 zk		uk ivk		xk i yk
k 0		k 0

150

n 1					n 1
uk xk vk yk				i uk yk vk xk .
k 0					k 0
				n 1
Если	существует	lim		f k zk		, то он называется интегралом			от
		zk	0	k 0
		n
функции f z по линии L и обозначается f z dz .
						L
Рассматривая предел
	n 1				n 1		n 1
lim	f k zk		lim		uk xk	vk yk i lim	uk yk	vk xk	,
zk 0	k 0		zk	0	k 0	zk 0	k 0
n			n			n
получим
		f z dz udx vdy i vdx udy .
		L			L	L

Следовательно, вычисление интеграла от функции комплексной переменной сводится к вычислению двух криволинейных интегралов от функций действительной переменной.

В комплексной плоскости параметрические уравнения линии

x x(t)y y(t)

удобно записывать в виде одного комплексного уравнения

z t x t iy t .

Если при этом z A, z B , то

f z dz f z t z ' t dt

L

Имеют место следующие свойства комплексного интеграла:

1. Если линия	L	является объединением	линий	L1 , L2 и	длина
пересечения		L1 L2	равна	0,	то
f (z)dz f (z)dz f (z)dz
L	L1	L2
2. Для любой постоянной имеет место равенство
f (z)dz f (z)dz
L		L

151

3. f z g z dz f z dz g z dz

L L L

4. f z dz f z dz

AB

BA

Замечание: если L - замкнутая линия на комплексной плоскости, ограничивающая односвязную область D то комплексный интеграл

f z dz определяется так же, но при условии, что интегрирование

L

происходит в направлении, оставляющем область D слева.

		z
Пример: Вычислить интеграл		dz	по окружности	z	1.
	L

Решение: параметрические уравнения окружности в комплексной форме имеют вид z t cos t i sin t , 0;2 . Значит, z ' t sin t i cos t и

	dz	2 sin t i cos t		2 sin t i cos t cos t i sin t
			cos t i sin t	dt	cos t i sin t cos t i sin t		dt
	z
L		0		0

2

i cos 2 t sin 2 t dt 2i .

0

Замечание: Пусть L - замкнутая линия, ограничивающая область,

содержащую точку 0. Тогда

dz

ln z

L . Поскольку

ln z ln i , то

L

z

при обходе линии L угол получит приращение 2

и, значит, функция

ln z при обходе этого контура получит приращение 2i .

Значит,

dz

ln z

L 2i

z

L

Пусть теперь

L - замкнутая линия, ограничивающая область, содержащую

точку a . Тогда

dz

dt

ln t

L'

2i .

z a

L

' t

L

152