заочникам / диф ур / Lectures - 3

Лекция 3(37) Дифференциальные уравнения первого порядка (окончание).

Уравнение в полных дифференциалах

В курсе лекций второго семестра было дано определение полного

дифференциала функции z	f (x, y) : dz	z	dx	z	dy .
		x		y
Определение: Дифференциальное уравнение		f (x, y)dx g(x, y)dy 0

называется уравнением в полных дифференциалах, если найдется функция

	двух переменных z F(x, y) такая, что	z		f (x, y) и	z	g(x, y) .
		x			y

Из теоремы о совпадении смешанных производных следует, что выражение

f (x, y)dx g(x, y)dy 0 будет

полным дифференциалом

тогда

и

только тогда, когда

f

g .

y

x

Пример

1:

Проверить,

являются

ли

дифференциальные

уравнения

2xy y 2 dx 2xy x2 dy 0 ,

y 2 dx x2 dy 0 уравнениями

в

полных дифференциалах.

Решение: 1)

2xy y 2

2x 2 y ,

2xy x2 2 y 2x

x

y

Получили

одинаковые

выражения,

значит,

уравнение

2xy y 2 dx 2xy x2 dy 0

является

уравнением

в

полных

дифференциалах.

2)

y 2

2 y ,

x2 2x .

Производные различны,

значит,

y

x

уравнение

y 2 dx x2 dy 0

не

является

уравнением

в

полных

дифференциалах.

Пример

2:

Найти

функцию,

для

которой

выражение

2xy y 2 dx 2xy x2 dy является полным дифференциалом

23

Решение: обозначим искомую функцию F(x, y) , тогда		F	2xy y 2 и,
		x
следовательно,	F(x, y) 2xy y 2 dx . При вычислении частной

производной по одной из переменных другая переменная рассматривается как постоянная, поэтому и при интегрировании по одной из переменных вторая переменная должна рассматриваться как постоянная. Значит, и «постоянная», которая появится при взятии неопределенного интеграла

2xy y 2 dx , вообще говоря, может зависеть от переменной y .

2xy y 2 dx x2 y y 2 x ( y)

( y) - пока неизвестная функция одной переменной.
Поскольку F x, y x2 y y 2 x y и F 2xy x2				, то
			y
		x2 y y 2 x y x2 2xy ' y и, следовательно,
	y
	x2	2yx ' ( y) 2xy x2 .Отсюда находим ' ( y) 0 ,
значит, ( y) C			и F(x, y) x2 y y 2 x C .

Замечание1: в последнем примере приведен общий метод нахождения функции по ее полному дифференциалу. Сначала интегрируется одна из известных частных производных функции, в результате получается выражение, содержащее неизвестную функцию одной переменной. Затем это выражение дифференцируется по второй переменной и приравнивается ко второй известной частной производной. Из полученного равенства находится неизвестная функция одной переменной.

Замечание 2: Если полный дифференциал функции равен нулю, то сама функция, очевидно, равна некоторой постоянной. Поэтому для решения

уравнения в полных дифференциалах достаточно найти функцию F(x, y) , для которой выражение f (x, y)dx g(x, y)dy является полным дифференциалом. Неявная функция одной переменной F(x, y) С будет общим решением такого дифференциального уравнения.

Пример: Проверить, что уравнение 2xydx x2 y 2 dy 0 является уравнением в полных дифференциалах и найти его общее решение.

24

Решение:

2xy 2x ,

x2 y 2 2x , значит, это уравнение есть

y

x

уравнение в полных дифференциалах.

F(x, y) 2xydx x2 y ( y)

F (x, y) x2 ' ( y) ;

x2 ' ( y) x2 y 2 ; ' ( y) y 2 ;

y

( y) y 2 dy

y3

C ; F (x, y) x2 y

y3

3

3

Общее решение уравнения:

x2 y

y3

C .

3

Метод Эйлера

Лишь очень немногие типы дифференциальных уравнений допускают интегрирование в квадратурах. В частности, уже такое несложное с виду

уравнение как y' x2 y 2 (уравнение Риккати3) в квадратурах не

интегрируется. Рассмотрим один метод приближенного решения дифференциальных уравнений первого порядка.

Постановка задачи: найти решение задачи Коши y' f (x, y) ,

y(x0 ) y0

на заданном интервале x0 ; xn .

Метод Эйлера: Поделим отрезок x0 ; xn точками

x1 , x2 ,..., xn 1

на части.

Для определенности

будем считать, что

x0

x1

x2 ... xn 1

xn .

Длину отрезка xi 1 ; xi

обозначим xi .

Поскольку y' f (x, y) ,

то угловой коэффициент интегральной кривой в

точке x

0

, y

0

равен

y'

f (x

0

, y

0

) .

Проведем через точку

x

0

, y

0

0

прямую

с

угловым

коэффициентом

y ' .

Уравнение этой

прямой:

0

y y

0

y'

x x

0

.

Если

интервал

x

0

; x

достаточно

мал,

то

0

1

интегральная кривая на этом интервале мало отличается от проведенной

3 Риккати Якопо Франческо (1676-1754) итальянский математик. Труды по интегральному исчислению и дифференциальным уравнениям.

25

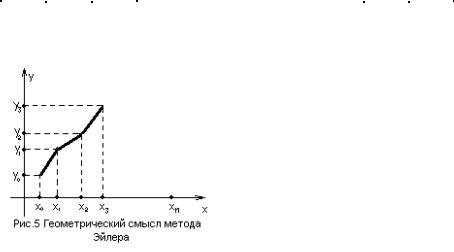
прямой

и можно приближенно считать, что в точке

x1

, y1

значение

искомой функции приближенно равно y y

0

y'

x

x

0

. Через точку

1

0

1

x , y

проводим прямую с угловым коэффициентом

y'

f (x , y ) и,

1

1

1

1

1

аналогично предыдущему, значение функции в точке

x2 , y2

считаем

приближенно равным y

2

y

y'

x

2

x

и т. д.

1

1

1

В результате получим таблично заданную функцию, значения которой в

точках	x1 , x2 ,..., xn 1 , xn приближенно равны значениям искомой функции
в тех же точках:
x0	x1		x2		……..		xn 1		xn
y0	y1		y	2	………		yn 1		yn
					Замечание: с геометрической точки
					зрения	вместо графика		искомой
					функции	получается некоторая
					ломаная,	называемая		ломаной
					Эйлера.

Таким образом, алгоритм метода Эйлера состоит в следующем: с помощью формул

yi

yi' f (xi , yi )

yi 1 yi' 1 xi xi 1 i 1,2,...n

последовательно заполняется таблица приближенных значений искомой функции в выбранных точках x0 , x1 , x2 ,..., xn 1 , xn .

Теорема (о ломаных Эйлера) Если существует ровно одно решение
задачи	Коши y'	f x, y ,	x	0	, y	0	, и при	этом	функция
z f (x, y) непрерывна, то любая				последовательность выходящих из
точки	x0 , y0 ломаных Эйлера, у которых длина наибольшего из звеньев
стремится к нулю,		приближается			на		интервале	x0 ; xn	к этому

единственному решению.

Без доказательства.

26

Для того чтобы найти приближенное значении искомой функции в какойлибо точке, отличной от точек x0 , x1 , x2 ,..., xn 1 , xn , можно применить

т. н. линейную интерполяцию, т. е. на каждом из интервалов xi 1 ; xi

заменить искомую функцию линейной функцией, график которой проходит
через точки	xi 1 , yi 1 и	xi , yi . Чтобы найти значение функции,

являющейся решением поставленной задачи Коши, в некоторой точке x ,
надо определить какому из интервалов	xi 1 ; xi эта точка принадлежит,

провести на этом интервале линейную интерполяцию и подставить число x в полученную линейную функцию.

	Пример:	Решить задачу Коши y '	2 y	,	y 1 1 на интервале 1;2 ,
			x
	разбивая интервал на 5 частей и найти приближенные значения функции
	y 1,1 и	y 1,7 .

Решение: составим таблицу из трех строк, занося в верхнюю строку значения независимой переменной, во вторую строку приближенные значения искомой функции, в третью – приближенные значения производной искомой функции.

Длина заданного интервала равна 1, по условию задачи он разбивается на 5 интервалов, значит длина каждого из маленьких интервалов равна 0,2 и

x0	1; x1				1,2; x2				1,4; x3					1,6; x5				1,8; x6 2
	x						1					1,2					1,4		1,6			1,8	2
	y						1
	y '
																		y '	f (x	, y	)
																		i	i	i		xi 1 :
																	yi 1		'
Дальше пользуемся формулами yi																			yi 1 xi
																		i 1,2,...n
y '	f (x					, y		)	2 y0				2 1		2		;
					0		0
0									x0			1
y	y	0	y' x x							0	1 2 1,2 1 1 0,4 1,4
1						0		1

27

y	'	f (x , y )											2 y1							2 1,4			2,333
1					1		1								x1			1,2
y	2	y			y' x					2		x						1,4 2,333 1,4 1,2 1,867
			1				1					1
y	'	f (x					, y		)						2 y2							2 1,867					2,667
	2					2		2
															x2			1,4
y	3	y		2	y'			x				x				2	1,867 2,667 1,6 1,4 2,400
							2				3
y	'	f (x					, y		)					2 y3							2 2,400						3,000
	3							3
					3										x3			1,6
y	4	y		3	y'			x			4	x					2,400 3,000 1,8 1,6 3,000
							3					3
y	'	f (x					, y		)						2 y4							2 3,000					3,333
	4					4		4
															x4			1,8
y	5	y		4	y'			x				x				4	3,000 3,333 2 1,8 3,667
							4				5
		x						1										1,2						1,4					1,6	1,8	2
		y						1										1,4						1,867					2,400	3,000	3,667
		y	'					2										2,333						2,667					3,000	3,333

Найдем теперь значения y 1,1 и y 1,7 .

Точка 1,1 1;1,2 . Составим уравнение прямой, проходящей через точки 1

	и 1,2:	x 1			y 1		;	y 2x 1. В точке 1,1	y 2 1,1 1 1,2
		1,2 1			1,4 1

y 1,1 1,2 .

Точка 1,7 1,6;1,8 . Составим уравнение прямой, проходящей через точки

	1,6 и 1,8:	x 1,6		y	2,4	;	y 3x 2,4 . В точке 1,7
		1,8 1,6		3	2,4

y 31,7 2,4 2,7 y 1,7 2,7 .

Существование и единственность решения задачи Коши

Теорема о ломаных Эйлера гарантирует стремление этих ломаных к решению при условии, что существует ровно одно, проходящее через точку

28

x0 , y0 решение, поэтому желательно уметь определять по виду уравнения существует ли решение задачи Коши и является ли оно единственным.

Теорема Пикара4 (о существовании и единственности решения задачи

Коши) Пусть функция

f (x, y) определена

в некоторой плоской области

D . Тогда, если в этой области непрерывна функция

f (x, y) и ее частная

производная

f

,

то

для любой точки

x

, y

D задача Коши

0

0

y

y' f (x, y) ,

y x

0

y

0

имеет единственное решение.

Пример: Проверить существование и единственность решения для задач

Коши: 1) y' 2

y'

y , y(0) 1

2)

2 y , y(1) 0 .

f (x, y) 2

Решение: Функция

y

непрерывна в любой точке верхней

полуплоскости

прямоугольной

системы координат

y 0 .

Частная

производная f

1

непрерывна

при

y 0 .

Значит, по

теореме

y

y

Пикара, задача Коши

y' 2 y ,

y(0) 1 имеет единственное решение,

т.к. по условию,

y0

1 0 .

y'

2

y(1) 0 нельзя сказать,

Про задачу Коши

y ,

что она имеет

единственное решение, т.к.

в

этом

случае

неравенство

y0 0 0 не

выполняется.

Рассмотрим подробнее, что происходит с решениями дифференциального

уравнения при

y0

0 . Для этого решим уравнение аналитически.

dy

dy

dx ;

dy

dx ;

2 y ;

y x C - общее решение

dx

2

y

2 y

дифференциального уравнения. Поскольку, преобразуя уравнение, его делили на y , то могли потерять решение y 0 . При подстановке

4 Пикар Эмиль (1856-1941) французский математик. Труды по дифференциальным уравнениям, теории функций.

29

		y 0				в уравнение y'
функции							2 y			получаем	тождество, значит,
функция	y 0					также является	решением			данного	дифференциального
уравнения.			1;0 проходят две интегральные кривые дифференциального
Через точку
уравнения:				y x 1 и y 0 , т.е. действительно, решение задачи Коши
y' 2			y(1) 0 не единственно.
	y ,

Контрольные вопросы:

1.Что называется уравнением в полных дифференциалах? Каков метод решения такого уравнения?

2.В чем состоит метод Эйлера приближенного решения задачи Коши для дифференциального уравнения первого порядка?

3.Сформулируйте теорему Пикара о существовании и единственности решения задачи Коши.

Задачи для самостоятельного решения:		f x, y ,	y x		y
1. Модифицировать метод Эйлера для задачи Коши	y'			0		0	на
интервале xn ; x0 , где xn x0 .
2. . Модифицировать метод Эйлера для задачи Коши	y'	f x, y ,	y x	0	y	0	на
интервале x n ; xn , если x0 x n ; xn .

Лекция 4(38) Дифференциальные уравнения порядков выше первого

Дифференциальное уравнение порядка n имеет вид F x, y, y' ,..., y n 0 , где F – заданная функция, x - независимая переменная, y - неизвестная функция.

Дифференциальные уравнения второго порядка

Геометрическая интерпретация: Поскольку производная функции в точке равна тангенсу угла наклона касательной, то дифференциальное уравнение

первого порядка F x, y, y' 0 устанавливает связь между координатами

точки на линии и углом наклона касательной к линии в этой точке. Можно дать аналогичную интерпретацию дифференциального уравнения второго

30

порядка F x, y, y' , y'' 0	: поскольку формула	y ''				задает
			3
		1 y ' 2
				2

кривизну графика функции в точке и зависит только от первой и второй производных, то уравнение F x, y, y' , y'' 0 , также зависящее от

координат точки и производных первого и второго порядков, устанавливает связь между координатами точки, углом наклона касательной и кривизной в этой точке.

Физическая интерпретация: поскольку скорость материальной точки равна производной по времени от пройденного пути, то дифференциальное

уравнение первого порядка F x, y, y' 0 устанавливает связь между

моментом времени x , координатой точки y и скоростью y ' материальной точки в этот момент времени. Аналогично, дифференциальное уравнение

второго

порядка

дает зависимость

между

моментом

времени

x ,

пройденным к этому моменту путем y ,

скоростью

y '

материальной точки

и ее ускорением y '' .

Основные задачи теории дифференциальных уравнений второго порядка:

1)

Найти общее решение уравнения F x, y, y' , y'' 0

2)

Задача Коши. Найти решение уравнения

F x, y, y' , y'' 0 ,

удовлетворяющее начальным условиям

y x

0

y

0

,

y' x

0

y' ,

0

где x

0

, y

0

, y' - заданные числа.

0

3)

Краевая задача. Найти решение уравнения F x, y, y' , y'' 0

на

промежутке

a;b , удовлетворяющее

граничным

условиям

y a A ,

y b B , где A, B - заданные числа.

Пример: Решением задачи Коши для уравнения

y ''

0

будет

3

1 y '

2

2

прямая,

проходящая через заданную точку M x0 , y0 под заданным углом

(тангенс которого равен y0' ) к оси абсцисс. Решением краевой задачи для

того же уравнения будет прямая, проходящая через две заданные точки

M1 a, A , M 2 b, B .

31

Уравнения, допускающие понижение порядка

1) Рассмотрим уравнение, содержащее только одну производную произвольного порядка и независимую переменную: F x, y n 0 . Такое

уравнение можно решить последовательным интегрированием производных.

Пример 1: Найти общее решение уравнения y IV x 3

Решение: По известной четвертой производной можно найти третью производную:

y '''			x 3 dx												1				C				,	по третьей производной можно найти вторую
													2x2									1
и т. д.
y ''										1					C					dx							1	C x C
																																		2
										2x2								1									2x				1
	'								1																				1				C1 x2
y											C x C												dx								ln x					C		x C
								2x							1							2							2			2					2		3
y						1			ln x							C x 2
																	1					C x C dx
																															3
						2											2								2
	1			x ln x x														C x				3				C x 2					C3 x C4
																		1									2
	2																			6							2

Пример 2: Материальная точка движется с ускорением, связь которого со

временем дается формулой a(t) 2sin 3t . В момент	времени	t0 0
координата точки была равна s(t0 ) 1, а скорость -	v(t0 ) 2	Найти

закон движения (изменение координаты в зависимости от времени). Решение: Поскольку скорость есть производная от пути, а ускорение – его вторая производная, то, по сути, требуется решить задачу Коши:

s'' (t) 2sin 3t , s(0) 1,								s' (0) 2 .
s' (t) 2 sin 3tdt					2	cos 3x C1
					3
s(t)			2	cos 3x C			dx		2	sin 3x C x C			.
												2
		3			1			9			1

32