заочникам / диф ур / Lectures - 3

тогда f x, y, z dV f x, y, z dV f2 x, y, z dV

V	V1	V2
2) Для любого числа :
	f x, y, z dV f x, y, z dV
	V	V

3) f x, y, z g x, y, z dV f x, y, z dV g x, y, z dV ,

V				V		V
если оба интеграла в правой части равенства существуют.
Без доказательства.
						Рассмотрим тело
						V , ограниченное
						поверхностями
						z f x, y ,
						z g x, y	и
						цилиндрической
						поверхностью	с
						образующей,
						параллельной оси
каждой точке этого тела задана функция u x, y, z .						OZ . Пусть	в
Обозначим через D проекцию тела V на координатную плоскость XOY .
Расставим пределы интегрирования по плоской области D :
b G( x)
	x, y, z dy dx ,
a	F ( x)
	b	G( x) g ( x, y)
тогда x, y, z dV				x, y, z dz dy		dx .
V	a F ( x) f ( x, y)

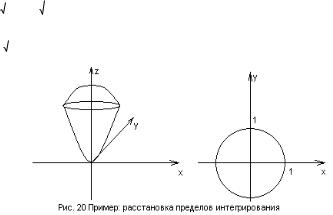
Пример:	Расставить пределы интегрирования в		интеграле xdV по
			V
области, ограниченной поверхностями x2 y 2 z 2			2, z x2 y 2 .
Решение:	Поверхность	x2 y 2 z 2 2 является сферой радиуса 2 ,
поверхность z x2 y 2		- параболоид вращения.

113

x

Проекцией полученного тела является круг радиуса 1:

z z 2 2 ,

z

2, z

2

1. Поскольку z x2

y 2 , то

1

2 x2 y 2

1

1 x2

xdV

xdz dy dx .

2

2

2

V

1

1 x

x

y

	2 y 2 z 2 2			,
	x 2	y 2	z
	x2	y 2	1.

Определение:

Пусть переменные x, y, z являются

функциями

независимых

переменных u, v, w :

x x u, v, w , y y u, v, w ,

z z u, v, w . Тогда определитель
				x		x	x
				u		v	w
	J u, v, w			y		y	y
				u		v	w
				z		z	z
				u		v	w
называется якобианом замены переменных.
Пример (цилиндрическая замена координат)
x cos, y sin, z z '
J , , z '			cos		sin 0
			sin		cos		0
			0			0	1
Теорема (о замене переменных)
Пусть x x u, v, w ,	y y u, v, w ,					z z u, v, w , эти функции

непрерывны и осуществляют взаимно однозначное отображение области V ' на область V , тогда

114

f x, y, z dV f x u, v, w , y u, v, w , z x, y, z J u, v, z dV

	V												V '
Без доказательства.
Пример:				Вычислить										интеграл						xdV по								области,				ограниченной
																				V
поверхностями x2 y 2														z 2 2, z x2							y 2 .
Решение:							Сделаем										цилиндрическую												замену			координат
x cos, y sin, z z
В круге x2					y 2 1 переменные															и изменяются независимо друг от
друга в пределах 0;1 , 0;2 , значит,
							1
				2					2 2
xdV
										cos dz d d
V					0		0			2
																													2
	2 2														2 2
	cos dz cos														dz cos
																							2 2
	2														2
1																				1
cos														d cos														3 d
					2 2					2												2 2
0																				0
		1														4			1					1 1											1
											2																			2	d 2		2
							2					d																	2
cos																4				cos				2											4
			0																0							0

				1		1			1							1				3		1
																				2
							tdt					cos					t
cos				2					4
						2										3						2
			2
8 2 7										8			2 7							02
				cos d											sin
12												12
				0

	1			8		2 7
			cos					.
	4				12

0 .

Приложение двойных и тройных интегралов к задачам геометрии и физики

Уже упоминалось, что двойной интеграл можно применять для вычисления объемов тел определенного вида (цилиндрический брус) и вычисления массы тонкой пластинки.

115

Кроме того, с помощью двойного интеграла можно вычислить площадь любой плоской фигуры. Выведем формулу для вычисления такой площади. Рассмотрим формулу для массы тонкой пластинки

m h x, y dS ,

D

и предположим, что плотность пластинки постоянна и равна . Тогда m h dS . Но, с другой стороны, масса пластинки постоянной

D

плотности равна m h S , где S - площадь основания пластинки. Из равенства h dS h S следует, что площадь любой плоской области

D

D может быть вычислена по формуле S dS

D

Приведем без доказательства формулы для вычисления моментов инерции плоской области D относительно осей координат и формул для координат ее центра тяжести

I x y 2 x, y dS ,	I y x 2 x, y dS ,
D	D
где x, y - плотность,

x0 1 x x, y dS , m D

y0 1 y x, y dS , m D

где x, y - плотность, m - масса тела.

В случае если плотность тела постоянна (тело однородно), то

			S					S
x			1		xdS , y			1		ydS ,
	0					0
				D					D

где S - площадь области D .

Пример1: Найти координаты центра тяжести плоской однородной фигуры, ограниченной линиями y x2 , y 1.

Решение:

Вычислим площадь фигуры, ограниченной линиями y x2 , y 1:

116

									1				1													1																				x3					1						1					1 4
		dS														dy dx													1			x2 dx x																				1							1
D									1 x2																1																					3					1						3					3 3
						3											3				1					1															3	1		x 1 x 2 dx
x												xdS																	xdy						dx
	0
						4 D											4 1 x2																								4 1
		3 1				x x3 dx															3 x 2														x 4					1
																																									0 ,					что и						следовало									ожидать,								т.к.
		4 1																			4					2									4					1
рассматриваемая фигура симметрична относительно оси OY .
						3											3				1					1
y												ydS																	ydy dx
	0
						4 D												4 1 x2
1										y 2					1		1							x 2 2												1 x 4
ydy
												2					2												2											2
x2																x2
																																																								1
						3			1		1															3						1			1 x					4						3						x	5							3					2					3
y																ydy dx																									dx							x														2
	0					4																				4										2										8						5							8										5
								1 x2																							1																									1									5
Из		формулы														массы							произвольного																				тела					m x, y, z dV																			можно
																																																				V

вывести формулу объема тела: V dV .

V

Пример2: Вычислить объем тела, ограниченного эллипсоидом

	x 2		y 2		z 2	1
	a 2		b2		c 2

Решение: Верхняя и нижняя половины эллипсоида, являющиеся графиками

функций двух переменных, задаются уравнениями z c

1

x 2

y 2

и

a 2

b2

z c 1

x 2

y 2

. Проекцией этого эллипсоида на плоскость XOY

a 2

b2

является эллипс

x 2

y 2

1.

a 2

b2

117

Сделаем замену переменных x aX , y bY, z cZ . Якобиан замены

	a	0	0
переменных равен J X ,Y , Z	0	b	0	abc . При такой замене
	0	0	c

переменных эллипсоид превращается в сферу

X 2 Y 2

Z 2

1,

а его

проекция – в окружность X 2 Y 2

1

1

1 X 2

1 X 2 Y 2

dZ

V abc

dY dX

1 1 X 2

1 X 2 Y 2

1 X 2

Y 2

dZ 2 1 X 2 Y 2 .

1 X 2 Y 2

1 X 2

При

вычислении

интеграла

2

1 X 2

Y 2 dY

воспользуемся

1 X 2

табличным интегралом

Y

a2

arcsin

Y

a2 Y 2 dY

a 2 Y 2

, считая a2

1 X 2 :

2

a

2

1 X 2

1 X 2

1 X

2

Y

2

2

2

2

Y

2

1 X

Y

dY

2

1

X

Y

arcsin

2

1 X

2

2

2

1 X

1 X

2

1 X

2

1

2

1 X

2

1 X 2

X

4

1 X 2

arcsin

2

2

1 X

2

4

1 X 2

arcsin 1 1 X 2

2

1

X 3

1

4

V abc

1 X 2 dX abc X

abc .

3

3

1

1

R ,

В частности, если эллипсоид

является

сферой радиуса

получится

известная формула объема шара V

4

R3 .

3

118

С помощью тройного интеграла можно вычислять моменты инерции произвольного объемного тела переменной плотности x, y, z

относительно осей координат и относительно координатных плоскостей:
I x	y 2	z 2 x, y, z dV , I y	x 2 z 2	x, y, z dV ,
V			V
		I z x2 y 2 x, y, z dV
		V
I zy	x 2 x, y, z dV , I xz		y 2 x, y, z dV ,
		V	V
		I xy z 2 x, y, z dV .

V

Кроме того, можно вычислять координаты центра тяжести произвольного

тела:

x

1

x x, y, z dV ,

y

1

y x, y, z dV ,

m

m

0

0

m

V

V

z

1

z x, y, z dV , где m - масса тела.

0

V

V

V

В

случае

постоянной

плотности: x

1

xdV , y

1

ydV ,

0

0

V

V

V

z

1

zdV , где V - объем тела.

0

V

Контрольные вопросы:

1.Что называется тройным интегралом? При каких условиях существует тройной интеграл? Сформулируйте свойства тройного интеграла.

2.Сформулируйте алгоритм сведения тройного интеграла к троекратному.

3.Как производится замена переменных в тройном интеграле? Что называется якобианом замены переменных? Что называется цилиндрической заменой переменных?

4.Как с помощью двойного интеграла вычисляются площадь, моменты инерции и координаты центра тяжести плоской области? Как с помощью тройного интеграла вычисляются площадь, моменты инерции и координаты центра тяжести пространственной области?

Задачи для самостоятельного решения:

1.Доказать теорему о свойствах тройного интеграла.

2.Доказать, что якобиан пространственной полярной системы координат равен

2 cos .

3.Доказать справедливость формул для вычисления моментов инерции и координат центра тяжести пространственного тела.

119

Лекция 14(48) Криволинейные интегралы

Криволинейные интегралы первого типа

Задача о массе кривой. На плоскости дана линия L , на которой непрерывно распределена плотность x, y . Требуется найти массу линии

в предположении, что если бы плотность была постоянной, то масса была бы равна произведению длины линии на плотность.

Между концами A и B линии L

произвольно			расставим			на		линии
точки	A1 , A2 ,..., An 1					и		для
однообразия			обозначений					будем
считать	A A0 ,			B An . На каждой
из дуг	Ai 1 Ai		произвольно				выберем
по точке		M i	xi , yi . Плотность						в
точке	M i xi , yi				равна	xi , yi			.
Если дуга		Ai 1 Ai		достаточно мала,					то
можно приближенно считать, что
плотность в любой точке этой дуги приближенно равна					xi , yi		.	Тогда
масса дуги Ai 1 Ai будет приближенно равна mi		xi , yi Si ,					где Si

- длина этой дуги. Масса всей линии L будет приближенно равна

mxi , yi Si

i 1n

				n
и в пределе		m	lim	xi , yi Si
			n	i 1
			Si 0
Определение: Пусть на плоскости дана некоторая линия L , в каждой точке
которой	задана	функция	f x, y . Поделим эту		линию	точками
A0 , A1 , A2 ,..., An		на более мелкие дуги и на каждой дуге			Ai 1 Ai	выберем
точку M i	xi , yi .

120

x ty t

z t ,t t1 , t2

n

xi , yi Si ,

Если существует

предел

lim

f

то

он

называется

n

i 1

Si 0

f x, y по линии L

криволинейным интегралом первого типа от функции

и обозначается f (x, y)dS , где dS - дифференциал дуги.

L

Замечание: криволинейный интеграл первого типа не

зависит

от

направления нумерации точек A0 , A1 , A2 ,..., An на линии (т.

е. не важно

обозначили ли мы

A A0

и продолжили нумерацию в сторону точки

B An или

наоборот,

начали нумеровать

точки, начиная

с

B A0 и

закончили в точке A An ).

Пусть линия L задана параметрическими уравнениями:

x t

y t

t t

1

, t

2

и при этом функции t , t и их производные ' t , '

t непрерывны

на интервале

t1 , t2 .

Тогда,

поскольку

дифференциал

дуги

равен

dS

dt , то

' t 2 ' t 2

t

f (x, y)dS 2

f t , t

' t 2 ' t 2 dt

L

t1

и вычисление криволинейного интеграла первого типа сводится к вычислению обыкновенного определенного интеграла.

Аналогично можно определить криволинейный интеграл первого типа по

пространственной линии	и, если эта	линия задана своими
параметрическими уравнениями

121

		t2
				t			t		t	dt
	f (x, y, z)dS f t , t , t
то			'	2		'	2	'	2		.
	L	t1

Имеют место следующие свойства криволинейного интеграла первого типа: Если линия L является объединением линий L1 , L2 и эти длина пересечения L1 L2 равна нулю, то

f (x, y)dS f (x, y)dS f (x, y)dS

L

L1

L2

Для любой постоянной имеет место равенство

f (x, y)dS f (x, y)dS

L

L

f (x, y) g x, y dS f (x, y)dS g(x, y)dS

L

L

L

Пример:

Вычислить интеграл

xydS ,

где L - четверть окружности

L

x2 y 2

1, заключенная в первом координатном углу.

Решение: 1 способ) Запишем параметрические уравнения окружности

x cos

y sin ,

0;2

тогда x'

sin, y' cos и

2

2

xydS cos sin

sin 2 cos 2 d cos sin d

L

0

0

2

sin

sin

2

2

1

sin d

.

0

2

0

2

2способ) Из x2 y 2 1 следует

y

1 x2 . В первом координатном

x

углу y

1 x2 , значит,

y '

.

1 x 2

122