заочникам / диф ур / Lectures - 3

n

операциях сходится ряд

M

x2

. Тогда, по признаку сравнения будет

n

n 0

x

1

сходиться

ряд

an x2n

. Поскольку

x2

- произвольное

число,

n 0

удовлетворяющее условию

x2

x1

, то ряд

an x n будет сходиться в

любой точке интервала x1 , x1 .

n 0

x x0 n

Рассмотрим

теперь ряд

an

и,

сделав замену

переменной

n 0

y x x0 ,

получим ряд

an y n , который сходится на

некотором

n 0

интервале y y1 , y1 . Возвращаясь к переменной x ,

получим, что ряд

x0 y1 , x0

y1 .

an x x0 n

сходится

на

интервале

Теорема

n 0

доказана.

Замечание: В частности, интервалом сходимости степенного ряда может

оказаться единственная точка x0

или вся числовая прямая.

Для

практического

нахождения

интервала

сходимости

ряда

x x0 n

an

можно применять

метод Даламбера, состоящий в

n 0

следующем: рассматривается предел

lim

a

n 1

x x

0

n 1

x x

lim

a

n 1

.

an x x0 n

0

an

n

n

Если этот предел меньше 1, то по признаку Даламбера, ряд сходится, если

больше – расходится. Решая неравенство		x x	0		lim	an 1		1 , находим
					n	a
							n

открытый интервал, в точках которого ряд сходится. Вне этого интервала за исключением, может быть, концов интервала, ряд расходится.

Для проверки сходимости на концах интервала нужно подставить каждое из этих двух чисел в формулу ряда и, получив числовые ряды, проверить их сходимость.

83

1

n 1

n

Пример1: Найти интервал сходимости ряда

x

n 1

n

Решение: lim

1 n 2 x n 1

n

x

lim

n

n 1

1 n 1 x n

n 1

n

n

x

lim

n

x

1

x

. Решаем неравенство

x

1 :

x 1;1 .

n n 1

x1 1 в

Теперь проверяем сходимость на концах интервала: Подставим

1

n 1

n

n 1

1

n

1

2n 1

ряд

x

:

1

1

.

n 1

n

n 1

n

n 1

n

n 1 n

Гармонический ряд расходится.

n 1

n

1

n 1

Подставим

точку

x2 1:

1

1

.

Получили

n

n

n 1

n 1

знакочередующийся ряд, удовлетворяющий условиям признака Лейбница:

1

1

, lim

1

0 . Значит, ряд сходится.

n 1

n

n n

Следовательно, интервалом сходимости данного ряда будет 1;1 .

x

n

Пример 2: Найти интервал сходимости ряда

n!

n 0

Решение: lim

x n 1

n!

x

lim

1

x

0 0

n 1 !

x n

n 1

n

n

Полученное неравенство 0 1верно при любых значениях переменной x , т. к. не зависит от этой переменной. Значит, ряд сходится при любых

значениях переменной и его интервалом сходимости является ; .

Пример 3: Найти интервал сходимости ряда n!x n .

n 0

Решение: lim

n 1 !x n 1

x

lim

n 1

x

.

n!x n

n

n

При любом значении переменной x 0 предел будет равен . При x 0

84

получается неопределенность 0 . Поэтому проверим сходимость

непосредственной подстановкой: n! 0n 0 0 0 ... 0 . Ряд

n 0

сходится.

Значит, данный ряд сходится в единственной точке x 0 .

Контрольные вопросы:

1.Какой ряд называется абсолютно сходящимся? Сформулируйте теорему об абсолютной сходимости.

2.Какой ряд называется знакочередующимся? Сформулируйте признак Лейбница сходимости знакочередующегося ряда. Используя доказательство признака Лейбница, покажите, что n-ый остаток ряда по модулю не превосходит n-го слагаемого ряда.

3.Что называется функциональным рядом? Почему функциональный ряд является некоторой функцией?

4.Что называется степенным рядом? Почему областью сходимости степенного ряда является некоторый числовой интервал? Сформулируйте метод Даламбера для нахождения интервала сходимости.

Задачи для самостоятельного решения:

1. Доказать принцип сходимости: для того, чтобы ряд an					сходился необходимо			и
				n 1
достаточно чтобы для любого числа 0 существовал такой					номер N, что при всех
n 0 , m 0 выполнялось неравенство		an 1	an 2 ...an m				.
2. Доказать справедливость признака Абеля: если ряд bn сходится, а числа an образуют
			n 1
монотонную и ограниченную последовательность, то ряд				an bn	сходится.
				n 1
3. Доказать справедливость признака Дирихле:			если	частичные	суммы ряда bn			в
							n 1
совокупности ограничены, а lim an 0 , то ряд			an bn сходится.
n			n 1

85

Лекция 10(44) Ряд Тейлора

Формула Тейлора10

Рассмотрим производные многочлена

p x a

0

a x a

2

x2

... a

n

xn

1

p' x a

2a

2

x 3a

x2

... na

n

xn 1

1

3

p'' x 2a

2

2 3a

x ... n n 1 a

n

xn 2

3

p''' x 2 3a

x ... n n 1 n 2 a

n

xn 3

3

…………………………………………………

p n

x

n n 1 n 2 ... 3 2a

n

При x 0 получим:

p 0 a0

0!a0

p

' 0 a

1!a

1

1

p'' 0 2a

2

2!a

2

p''' 0 2 3a

3

3!a

3

……………………….

p(n) n n 1 ... 3 2a

n

n!a

n

Значит, a

p 0

, a

p ' 0

,

a

p ''

0

,…., a

p n 0

,

0

2

n

0!

1

1!

2!

n!

p x

p 0

p' 0

p'' 0

2

p n 0

n

p

i 0

x

x

...

x n

xi

0!

1!

2!

n!

i 1

i!

Если в этой формуле заменить x на x x0 , получим общую формулу

p x

p x0

p ' x0

x x

p '' x0

x x

2 ...

0

0

0!

1!

2!

,

p

n x

n

p

i x

0

n

0

i

x x0

x

x0

n!

i!

i 1

называемую формулой Тейлора для многочлена.

Пусть

f x

- произвольная функция,

имеющая в точке x0

производные

f ' x

0

, f

'' x

0

,..., f n x

0

. Сопоставим этой функции многочлен

10 Тейлор Брук (1685-1731) английский математик.

86

lim

x x0

p

x

f x0

f ' x0

x x

f '' x0

x x

2

...

n

0!

0

2!

0

1!

f n x

0

n

n

f

i x

0

i

x

x0

x x0

n!

i!

i 1

Теорема (о порядке приближения функции многочленом) Пусть

f x -

произвольная

функция,

имеющая

в

точке

x0

производные

n

f i x

0

i

f ' x0 , f '' x0 ,...,

f n x0

, и пусть

pn x

x x0

, тогда

i!

f x pn x o x x0 n

i 1

Доказательство:

обозначим

rn x f x pn x .

Из

определения

многочлена

pn x следует, что

r

x

0

r ' x

0

r

'' x

0

... r n

x

0

0

n

n

n

n

При n 1

получим:

r1 x r x0

lim

r1 x

lim

r1 x 0

lim

r '

x

0 .

0

x x0 x x

x x0

x x

x x0

x x

1

0

0

0

При n 2 получим:

r2' x r2' x0

lim

r2 x

lim

r2' x

1

lim

1

r

'' x

0 ,

x x0 2

2 x x0

x x0

x

x0

2 x

x0

x x0

2 2

0

здесь воспользовались правилом Лопиталя.

При n 3 получим:

r x

lim

r '

x

1

r '' x

lim

3

3

lim

3

x x0

2 x x0

x x0

3

x

x0 3 x x0

2

3 x x0

1

lim

r3'' x r3'' x0

1

r

''' x

0

6 x x0

x x

0

6 3

0

здесь дважды воспользовались правилом Лопиталя.

В общем случае для доказательства равенства

будет n 1раз воспользоваться правилом Лопиталя.

rk x			0 нужно
x x	0	k

Теорема доказана.

87

Замечание: из доказанной теоремы следует, что формулу Тейлора можно использовать для вычислений приближенных значений дифференцируемых функций:

f x

f x0

f ' x0

x x

f '' x0

x x

2

...

1!

0

2!

0

0!

f n x

0

n

n

f i x

0

i

x x0

x x0 , причем, чем больше число

n!

i!

i 1

n , тем приближение лучше. Данная приближенная формула называется

формулой Тейлора. При x0 0 ее также называют формулой Маклорена11.

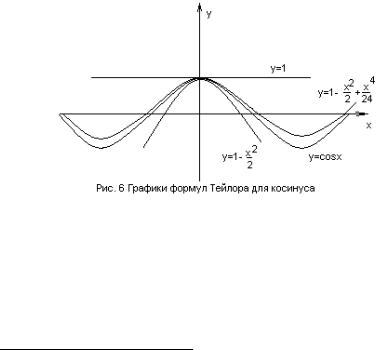
Пример: Рассмотрим функцию	f x cos x и составим для нее формулы
Тейлора при n 0,1,2,3,4 и x0	0 .

f ' x sin x; f '' x cos x; f ''' x sin x; f 4 x cos x f ' 0 0; f '' 0 1; f ''' 0 0; f 4 0 1.

p0 x f (0) 1
p			x f (0) f ' 0 x 1 0 x 1
1						f '' 0
p			x f (0) f ' 0 x					x 2	1		x 2
	2
				2					2
p				x f (0) f ' 0 x		f '' 0		x 2		f ''' 0			x3	1	x 2
		3
				2					6					2

11 Маклорен Колин (1698-1746) – шотландский математик. Труды по математическому анализу, теории кривых, механике.

88

p		x f (0) f ' 0 x	f '' 0	x2		f ''' 0	x3		f 4 0	x4	1	x2		x 4
	4
		2			6			24			2		24

Каждый следующий многочлен четной степени все лучше и лучше будет
приближать функцию	f x cos x на все большем и большем интервале.
	Ряд Тейлора
Пусть функция f x	имеет на промежутке x x0 , x x0 производные

любых порядков. Тогда, в связи с тем, что формула Тейлора при увеличении степени n все лучше и лучше приближает функцию, естественно считать

f x

f x0

f ' x0

x x

f '' x0

x x

2 ...

0

0

0!

1!

2!

f

n

x0

f

i

x0

x x0 n ...

x x0 i .

n!

i!

i 1

x0

f

i

x x0 i

Определение: Степенной

ряд

называется

рядом

i!

f x . При

i 0

Тейлора функции

x0

0

этот

ряд

называют

также

рядом

Маклорена. Функцию rn x f

x

n

f

i

x0

x x0 i o x x0 n

i 1

i!

называют остатком ряда Тейлора.

Пример 1:

Найдем ряды

Маклорена

функций

y

e x ,

y

2

sin x ,

1

y3 cos x ,

y4 ln 1 x , y5

1 x .

Решение: 1)

y e x : y'

y'' ... y n ... e x ,

y 0 y' 0 y'' 0 ... y n 0 ... e0

1.

1

1

1

x

n

e x

x

x 2

...

0!

1!

2!

n 0

n!

В предыдущей лекции было показано, что интервал сходимости степенного

	x	n
ряда			равен ; .
i 0	n!

89

	2) y sin x : y'	cos x, y'' sin x, y'''							cos x, y 4 sin x и т. д.
	y 0 0, y' 0 1, y'' 0 0, y''' 0 1, y 4 0 0 т.е.
	последовательность значений производных в точке 0 выглядит так:
	0,1,0,-1,0,10,-1,0,1,0,-1 и т.д.
		1				1				1 n 1 x 2n 1
	sin x 0				x 0			x3 ...
		1!				3!				2n 1 !
								n 0

Можно показать, что промежутком сходимости этого ряда также будет вся
числовая прямая ;
3) y cos x : y' sin x, y'' cos x, y''' sin x, y 4									cos x и т.д.
y 0 1, y' 0 0, y'' 0 1, y''' 0 0, y 4 0 1 т.е.
последовательность значений производных в точке 0 выглядит так:
1,0,-1,0,10,-1,0,1,0,-1,0 и т.д.
	1		1			1	n	x	2n
cos x 1 0		x 2 0		x 4	...
						2n !
2!			4!		n 0

И здесь можно показать, что промежутком сходимости этого ряда также

будет вся числовая прямая ; .

4) y ln 1 x :

y ' 1 x 1 ,

y''

1 x 2 ,

y''' 2 1 x 3 ,

y 4 2 3 1 x 4 ,

y 5

2 3 4 1 x 5 .

Очевидно,

что

y n 1 n 1 n 1 ! 1 x n

и

y n 0 1 n 1 n 1 !.

1

n 1

1

n 1

n

Значит, ln 1 x 0

n 1 !x n

x

.

n 1

n!

n 1

n

В предыдущей лекции было показано, что интервалом сходимости этого
ряда является 1;1 .		y		1 x	,	y		1 1 x	,
5)	y 1 x :
			'	1			''	2

y''' 1 2 1 x 3 и т.д.

y 0 1, y' 0 , y'' 0 1 , y''' 0 1 2 и т.д.

1 x	1 x			1 x2			1 2 x3	...
				2!			3!
В частности,	1	1	x x2		x3	... ,

1 x

Можно показать, что промежутком сходимости этого ряда является 1;1 .

90

Замечание: можно заметить, что в ряде Маклорена нечетной функции y sin x суммируются только нечетные степени переменной, а в ряде Тейлора четной функции y cos x суммируются четные степени

переменной. Это не случайно: можно доказать что у любой четной функции коэффициенты при нечетных степенях переменной в ряде Маклорена будут равны 0, а у нечетной функции будут равны 0 коэффициенты при четных степенях

Пример 2: составить ряды Маклорена функций y e x2 ,

y cos x .

Решение: 1)

y e x2 : обозначим t x2 , тогда

y et 1 t

t 2

t 3

... 1 x2

x4

x6

...

2!

3!

2!

3!

2) y cos

x : обозначим t x , тогда

cos t 1

1

t 2

1

t 4

... 1

x

x2

...

2!

4!

2!

4!

Замечание: этот метод, называемый метод подстановки не всегда приводит к нужному результату. Например, при нахождении ряда

Маклорена функции y sin x этот метод в ответе не дал бы степенного ряда.

Остаток ряда Тейлора в форме rn x o x x0 n не дает возможности

вычислять значения функции с заданной точностью, поэтому часто используются другие формы остатка, удобные для приближенных вычислений.

Пусть дана функция

y

f (x) на промежутке x0 ; x0

и существуют

непрерывные производные

f ' x , f '' x ,..., f n 1 x .

r

x f

x f x

f ' x0

x x

f '' x0

x x

2

0

0

0

n

1!

2!

f n x

0

x x

n

n! 0

Зафиксируем некоторое число x x0 ; x0 и, заменив постоянную x0 на переменную z , составим вспомогательную функцию

91

f ' z

f

'' z

2

f n z

n

z f x f z

x z

x z

...

x z

1!

2!

n!

Очевидно, что x0

rn x , x

0 .

Кроме того,

''

z

f

'

z

'''

z

f

''

z

' z f ' z

f

x

z

f

x z 2

x z

...

1!

1!

2!

1!

f n 1 z

x z

n

n!

x0 ; x

Пусть x - некоторая функция,

непрерывная на промежутке

и

такая, что на этом промежутке ' x 0 . Тогда по теореме Коши найдется

число c x0 ; x такое, что

x x0

' c

' c .

x x

0

0 rn x

f n 1 c

x x

n

n!

0

Следовательно,

, откуда:

x x0

' c

r x

x

x

0

f n 1 c

x c

n

. Различным образом выбирая

' x

n

n!

функцию x , можно получать различные формы остатка. В частности,

если x x z n 1 , получим	r	x	f n 1 c			x x		n - остаток в
			n 1 !
	n						0

форме Лагранжа.

Приближенные вычисления с помощью формулы Тейлора

Пользуясь формулой Тейлора с остатком в форме Лагранжа можно вычислять приближенные значения различных функций с заданной точностью

Пример 1: вычислить e с точностью 0,01

92