заочникам / диф ур / Lectures - 3

В первом координатном углу на									окружности						x2 y 2			1		переменная
x изменяется в пределах						x 0;1 .			Дифференциал дуги									линии, заданной
																dx , значит
явным уравнением			y f x , равен								1 f ' x 2
	1							x					2	1			x 2		1	1
				2
xydS x 1 x														dx xdx
						1				2							2		.
L	0					1 x								0					0	2

Криволинейные интегралы второго типа

Определение: Пусть на плоскости задана некоторая линия L , в каждой точке которой задана функция f x, y . Поделим эту линию точками

A0 , A1 , A2 ,..., An на более мелкие дуги и на каждой дуге Ai 1 Ai выберем
точку M i xi , yi .
	n	xi , где xi - проекция вектора
Если существует предел lim	f xi , yi
n	i 1
xi 0

_____

Ai 1 Ai на ось OX ,то он называется криволинейным интегралом второго типа от функции f x, y по линии L и обозначается f (x, y)dx .

L

Замечание 1: аналогично можно проектировать дуги Ai 1 Ai не на ось OX ,

а на ось OY . Получающийся в этом случае предел также называется

криволинейным интегралом второго типа от функции f x, y по линии L

и обозначается f (x, y)dy . В общем случае, если на линии L заданы две

	L
функции f x, y и			g x, y , то	можно рассматривать предел суммы
	n	xi	g xi , yi yi	также называемый криволинейным
lim	f xi , yi
n	i 1
xi 0				f x, y по линии L и обозначаемый
интегралом второго типа от функции

f (x, y)dx g(x, y)dy .

L

123

Замечание 2: аналогично, рассматривая три функции трех переменных и предел соответствующей суммы, можно определить криволинейный интеграл второго типа по пространственной линии:

f (x, y, z)dx g(x, y, z)dy h x, y, z dz

L

Замечание 3: В связи с тем, что в определении криволинейного интеграла второго типа под знаком суммы в качестве множителя присутствует

проекция вектора, то при изменении нумерации точек A0 , A1 , A2 ,..., An на противоположную, интеграл изменит знак на противоположный:

f (x, y)dx g(x, y)dy f (x, y)dx g(x, y)dy

AB BA

Имеют место следующие свойства криволинейного интеграла второго типа: 1) Если линия L является объединением линий L1 , L2 и длина их пересечения L1 L2 равна нулю, то интеграл по линии L равен

сумме интегралов по линиям L1 , L2 .

2)Постоянный множитель можно выносить за знак интеграла

3)Интеграл от суммы функций равен сумме интегралов

Пусть линия L задана параметрическими уравнениями

x ty tt t1 , t2

и при этом функции t , t и их производные ' t , ' t непрерывны на интервале t1 , t2 . Тогда

	t	f t , t ' t g t , t ' t dt
f (x, y)dx g(x, y)dy 2
L	t1

и вычисление криволинейного интеграла второго типа сводится к
вычислению обыкновенного определенного интеграла.
Если линия L	является графиком функции y h x на промежутке
	x
x1 , x2 , то f (x, y)dx g(x, y)dy 2 f x, h x g x, h x h' x dx
L	x1

Аналогично можно определить криволинейный интеграл первого типа по пространственной линии, если эта линия задана своими параметрическими уравнениями.

124

Пример

1:

Вычислить интеграл

xdx ydy

по

участку

параболы

x 0;1 .

L

y x 2 ,

Решение: dy 2xdx

1

1

x 2x3 dx

xdx ydy xdx x 2

2xdx

L

0

0

x2

x 4

1

1

1

1

2

2

2

2

0

Вычислить

интеграл

Пример

2:

y 2 dx x2 dy

по

контуру

квадрата

L

x 0;1 ,

y

0;1 при условии, что

обход линии совершается против часовой

стрелки.

Решение:

обозначим

стороны

квадрата

L1 , L2 , L3 , L4 как

показано на

рисунке.

Эти

линии

можно

задать

параметрическими уравнениями:

x t

x 1

x t

x 0

L :

y 0

; L

2

: y t

; L

3

:

y 1

; L

4

:

y t

1

0;1

t

t 0;1

t 1;0

t 1;0

y 2 dx x2 dy y 2 dx x2 dy y 2 dx x2 dy y 2 dx x2 dy

L

L1

L2

L3

y 2 dx x2 dy

L4

1

1

y 2 dx x 2 dy 02 dt t 2 0 0 ;

y 2 dx x 2 dy t 2 0 12 dt 1;

L1

0

L2

0

0

1

y2dx x2dy 12 dt t 2 0 1;

y2dx x2dy t 2 0 0dt 0

L3

1

L1

0

y2dx x2dy 0 1 1 0 0

L

125

Независимость интеграла от пути. Формула Грина.

Теорема

(о

независимости

интеграла

от

пути) Если

выражение

f x, y dx g x, y dy

является

полным дифференциалом,

то интеграл

f (x, y)dx g(x, y)dy зависит

только от

начальной и конечной

точек

L

интегрирования и не зависит от линии L , их соединяющей .

Доказательство: Пусть линия L

задана параметрическими уравнениями

x t

y t

t t

1

, t

2

Поскольку

f x, y dx g x, y dy - полный дифференциал, то существует

функция

F x, y такая, что

F

f x, y ,

F

g x, y .

Поскольку

x

y

переменные

x, y

являются

функциями

параметра

t ,

то

F x, y F x t , y t F t ;

dF

dt

f (x, y)dx g(x,

L

t2	dF	dt F t		t2
	dt			t1
t
1

Fx

y)dy

F t2

dx

F dy

F

' t

F

' t ;

y

x

y

dt

dt

F dx

F dy

t

F

F

2

' t dt

' t dt

L x

y

t

x

y

1

F t1 F x2 , y2 F x1 , y1 . Теорема

доказана.

Теорема (формула Грина) Пусть плоская область D ограничена линией
L , а функции x, y , x, y и их первые частные производные
непрерывны в области D , тогда
	x, y dx x, y	dy
						dS
L			D	x		y

Доказательство: Принято считать, что линия L обходится в направлении против часовой стрелки.

126

Рассмотрим сначала область, ограниченную линиями x a, x b , y f x , y g x , тогда

		b g x
		dS	dy dx .
D	y	a f x y

g x

x, y

g x

x .

y

dy

f x x, g x x, f

f x

b

b

b

x, g x x, f x dx x, g x dx

x, f

x dx

a

a

a

x, y dx x, y dx x, y dx x, y dx .

DC

AB

DC

BA

Поскольку

x, y dx x, y dx 0 (на этих отрезках переменная x

AD

CB

постоянна и поэтому ее дифференциал равен нулю), то

dS

x, y dx x, y dx x, y dx x, y dx

D

y

DC

CB

BA

AD

x, y

dx

(знак

минус появился из-за

того,

что

положительным

L

направлением интегрирования

считается

направление

против

часовой

x

x, y dy .

стрелки).

Аналогично доказывается,

что

dS

D

L

Значит,

поскольку

интеграл

от суммы

равен

сумме

интегралов,

127

	x, y dx x, y dy
							Эту же формулу нетрудно
						dS .
L			D	x		y
доказать, когда область		D ограничена тремя,					двумя или одной линией.
Теорема доказана.

Контрольные вопросы:

1.Что называется криволинейным интегралом первого типа? Каковы его свойства?

2.Как свести криволинейный интеграл первого типа к обыкновенному интегралу в случае параметрического задания линии, в случае явного задания линии в прямоугольной и полярной системах координат?

3.Что называется криволинейным интегралом второго типа? Каковы его свойства? Как свести криволинейный интеграл второго типа к обыкновенному интегралу?

4.Каково условие независимости криволинейного интеграла от пути интегрирования? Какова связь двойного интеграла с криволинейным?

Задачи для самостоятельного решения:

1.Доказать свойства криволинейного интеграла, сформулированные в лекции.

2.Доказать, что если плоская область D ограничена линией С, то ее площадь можно найти по

любой из следующих формул: S xdy ,	S ydx , S xdy ydx .
C	C	C

Лекция 15(49) Начальные понятия теории функций комплексной переменной

Расширенная комплексная плоскость

Пусть дана прямоугольная система координат XYZ в пространстве. Будем, как обычно, интерпретировать комплексные числа как векторы в плоскости

XOY .

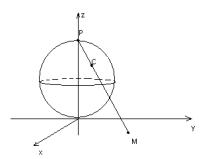
Рассмотрим сферу S (сфера Римана), касающуюся плоскости XOY в начале координат. Из верхней точки P сферы проведем луч, пересекающий эту сферу еще в какой либо точке С ; луч PC пересечет плоскость XOY в некоторой точке M .

128

Рис. 26 Сфера Римана

Таким образом можно установить взаимно однозначное соответствие между всеми точками сферы, за исключением точки P и всеми точками плоскости. Чем ближе точка С будет расположена к точке P , тем дальше от начала координат будет находиться точка M . В пределе, при C P

получим луч, параллельный плоскости XOY . Будем считать, что точке P на сфере соответствует бесконечно удаленная точка плоскости, которую будем обозначать .

Определение: множество всех точек комплексной плоскости вместе с точкой называется расширенной комплексной плоскостью.

Множество всех комплексных чисел обозначается C , а множество всех

точек расширенной комплексной плоскости - C .

Определение: -окрестностью точки z0 комплексной плоскости называется множество точек z , удовлетворяющих условию z z0 .

-окрестностью точки называется множеств точек расширенной комплексной плоскости, удовлетворяющих условию z

Замечание 1: -окрестность точки z0 представляет из себя открытый круг радиуса с центром в точке z0 . -окрестность точки является

расширенной комплексной плоскостью с удаленным из нее замкнутым кругом радиуса с центром в начале координат.

Рис. 27 Окрестности конечной и бесконечной точек

129

Определение: Множество точек D на расширенной комплексной плоскости называется открытой областью, если для любой точки z D найдется -окрестность, все точки которой принадлежат множеству D .

Предел последовательности комплексных чисел. Комплексные ряды.

Определение:	число	a называется пределом последовательности an
(записывается	lim an	a ), если для любого (как угодно малого)					числа
	n
0 найдется номер			N	такой, что для всех номеров n N			будет
выполнено неравенство			an	a		.

Теорема (о нахождении комплексного предела) Пусть дана

последовательность комплексных чисел zn xn

iyn

Если lim xn

x0

и lim yn

y0

, то lim zn

x0 iy0 .

n

n

n

Доказательство:

Пусть дано число 0 ,

тогда по определению предела

последовательности действительных чисел найдется номер

N1 такой, что

для всех номеров n N

x

, а

1

будет выполнено неравенство

x

n

0

2

N 2

n N2

также найдется номер

такой, что для всех номеров

будет

выполнено неравенство

y

n

y

0

. Пусть

N - наибольшее из чисел

2

N1 , N2 ,

n N будут

тогда

для

всех

номеров

верны неравенства

x

n

x

0

и

y

n

y

0

.

2

2

Рассмотрим

xn x0 i yn y0

:

zn z0

xn x0 2 yn y0 2

2

2

xn x0 2 yn y0 2

2 .

2

2

Теорема доказана.

130

Пример:

Найти предел последовательности z

1 n 1 i

n

n

Решение:

lim z

lim

1

i lim

n 1

0 1 i i .

n

n

n n

n

n

Теорема

(предел

и

арифметические операции)

Если

lim zn

z0 и

n

lim tn

t0 , то

n

zn

z0

1) lim

tn

t0

n

zn

z0

2) lim

tn

t0

n

zn tn z0 t0

3) lim

n

z

n

z

0

4) lim

, при условии, что t

0

0

t0

n tn

Доказательство: Пусть zn

an

ibn ,

tn cn

id n , z0

a0

ib0 ,

t0 c0

id 0 .

1) lim z

n

t

n

lim

a

n

c

n

i b

d

n

lim a

n

c

n

i lim b

d

n

n

n

n

n

n

n

a0 c0 i b0 d0

z0 t0 .

2) lim z

n

t

n

lim a

c

i b d

n

lim a

n

c i lim b

d

n

n

n

n

n

n

n

n

n

n

a0 c0 i b0 d0

z0 t0 .

3) lim z

n

t

n

lim a

n

c

n

b d

n

i a

n

d

n

b c

n

lim a

c

n

b d

n

n

n

n

n

n

n

n

i lim andn bncn

a0c0 b0d0 i a0d0

b0c0 z0t0

n

z

n

a ib

a c b d

n

i b c a d

n

4) lim

lim

n

n

lim

n

n

n

n

n

n

d

n t

n

n c id

n

n

c

2

2

n

n

n

a0c0 b0d0 i b0c0 a0d0

z0

.

c

2

d 2

t

0

0

0

Теорема доказана.

Определение:

Пусть

задана

последовательность

комплексных

чисел

z1 , z2 ,..., zn ...

Составленная

из

этих

чисел

сумма

131

z1 z2	... zn	... zn называется бесконечным рядом, а числа
		n 1

z1 , z2 ,..., zn ... называются элементами ряда.

Определение: Элементы последовательности A1 z1 , A2 z1 z2 , …,

An z1 z2 ... zn … называются частичными суммами ряда zn .

n 1

Определение: Если последовательность A1 , A2 ,..., An ... имеет конечный

предел, то этот предел называется суммой ряда, а сам ряд называется сходящимся. Если последовательность не имеет предела или имеет бесконечный предел, то ряд называется расходящимся.

Замечание: Как и в случае предела последовательности, проверка сходимости числового ряда комплексных чисел сводится к проверке сходимости двух рядов действительных чисел.

Имеют место теоремы, аналогичные теоремам для рядов действительных чисел:

Теорема (об остатках ряда)

1) Если ряд zn сходится, то сходится и любой и его остатков

n 1
2) Если сходится какой-либо остаток zn	ряда zn , то сходится и ряд
n k 1	n 1
zn .
n 1

Теорема (сходимость и линейные операции)

1) Если сходится ряд z1 z2 ... zn ... zn , то сходится и ряд

					n 1
сz1 сz2 ... сzn ... сzn , где с - любое комплексное число.
			n 1
2)	Если	сходятся	ряды		z1 z2 ... zn	... zn
						n 1
и	t1 t2	... tn ... tn ,		то	сходится	и	ряд

n 1

132