заочникам / диф ур / Lectures - 3

Замечание: символом CD

Интеграл типа Коши

будем обозначать дополнение области D до всей комплексной плоскости, т.е. множество всех точек комплексной плоскости, не принадлежащих области D .

Символом D будем обозначать замыкание области D , т.е. область D в объединении с ее границей.

Теорема Коши (о независимости интеграла от пути)

Если функция f z аналитична в односвязной области D , то интеграл

f z dz по незамкнутой линии L , лежащей в области D , зависит только

L

от начальной и конечной точек интегрирования и не зависит от формы линии L .

Доказательство: если	f z u x, y iv x, y , то
f z dz	udx vdy i vdx udy
L	L			L
Поскольку функция f z u x, y iv x, y аналитична, то имеют место
формулы Коши-Римана	u	v ,	v	u . Первая из этих формул
	x	y	x	y

означает, что под знаком интеграла vdx udy находится полный

L

дифференциал и, значит, этот интеграл не зависит от пути интегрирования. Вторая формула является условием того, что под знаком интеграла

udx vdy тоже находится полный дифференциал, и он также не

L

зависит от пути интегрирования. Теорема доказана.

Следствие: если функция f z аналитична в односвязной области D , и

L- замкнутая линия в этой области, то

f z dz 0

	L
Доказательство:	выберем на замкнутой линии L две произвольные
различные точки А и В, две полученные незамкнутые линии обозначим L1
и L2 . На линии	L1 выберем произвольную точку С. А на линии L2 - точку
D.

153

Рис. 38 Следствие из теоремы Коши

Тогда, по теореме Коши	f z dz	f z dz .
	ACB	ADB
Поскольку f z dz f z dz , то
ADB	BDA

f z dz	f z dz f z dz		f z dz f z dz 0 .
L	ACB	BDA	ACB	ADB

Определение: Связная область D называется n-связной, если ее граница

состоит из n непересекающихся линий L0 , L1 ,..., Ln 1
Обобщенная теорема Коши.
Если функция f		z аналитична в открытой односвязной области							D ,
ограниченной линией L , и непрерывна в замкнутой области D , то
		f z dz 0 .
		L
Без доказательства.
Следствие:	Пусть	функция	f z аналитична		в открытой n -связной
области D и непрерывна в замкнутой области,				полученной из области					D
присоединением ее границы			L L0 L1 L2	... Ln . Тогда
			n
	f z dz f z dz 0 .
	L0	k 1 Lk							z
Замечание:	Это	равенство	остается верным,		если функция			f

аналитична в открытой односвязной области D и непрерывна в замкнутой области D кроме конечного числа точек z1 , z2 ,..., zm , для которых верно

равенство

lim z zk f z 0

z zk

154

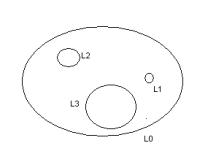
Рис. 39 Следствие из обобщенной теоремы Коши

Теорема (интегральная формула Коши) Если функция f z аналитична в открытой односвязной области D и непрерывна в замкнутой области,

поученной из области D присоединением ее границы L , то

1

f t

dt

f z ,

если

z D

2 i

t z

если

z CD

0,

L

f t

Доказательство: Если z CD ,

то функция

аналитична в области

z

f tt

D

и

по

теореме

Коши

0 .

Пусть

z D :

t z

L

1

f t dt

1

f t f z f z

dt

2i

t z

2i

t z

L

f t f

z

L

f z

1

dt

dt

.

2i

t z

2i

t z

L

f t f z

L

Функция t

удовлетворяет условию lim t z t 0 ,

t z

t z

значит,

1

f t f

z

dt 0 .

2i

t z

L

Второй интеграл

f z

dt

1

dt

1

f z

f z

2i f z .

2i

t z

2i

t z

2i

L

L

Теорема доказана.

155

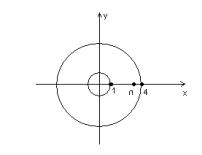
Пример: 1) вычислить интеграл

cos tdt

, если L - окружность

z

1

t

L

2)

cos tdt

, если L - окружность

z

4

t

L

Решение: Из интегральной формулы Коши следует, что

f t dt

2 if z , если

z D

L t z

0,

если

z CD

Рис. 40 Пример: вычисление комплексных интегралов

Поскольку точка z

находится вне круга

z

1,

то

cos tdt

0 .

t

z

1

Точка z попадает в круг

z

4 , то

cos tdt

2i cos 2i .

t

z

4

Интеграл типа Коши

Пусть L - линия

на комплексной

плоскости,

на

которой задана

непрерывная функция

f z . В любой точке комплексной плоскости, не

лежащей на линии L ,

функция

f t

непрерывна и, значит, существует

t z

f t dt

1

интеграл F z

, называемый интегралом типа Коши.

2i

t z

L

156

Замечание: в отличие от предыдущих рассуждений, здесь функция f z

предполагается только непрерывной, но не аналитической. Значит, к интегралу типа Коши не применима интегральная формула Коши.

Теорема (об аналитичности интеграла типа Коши)

В любой точке комплексной плоскости,

кроме точек, лежащих на линии L ,

интеграл типа Коши является аналитической функцией и при этом

F ' z

1

f t dt

.

2i

2

L

t z

Доказательство: рассмотрим отношение приращения функции к

приращению аргумента:

F z z F z

1

f t dt

1

f t dt

z

2i z

t z z

2i z

t z

L

L

f t dt

1

1

1

1

f t

dt

.

2i z

L

t z z

t z

2i

L t z t z z

lim

F z z F z

1

f t dt

. Теорема доказана.

2

z 0

z

2i L t z

Следствие 1: F n z

n!

f t dt

.

n 1

2i

L t z

f t имеет в любой

Следствие 2: Аналитическая в области D функция

точке этой области производные любых порядков.

Контрольные вопросы:

1.Что называется производной функции комплексной переменной? Что такое условия Коши-Римана? Какая функция называется аналитической?

2.Как определяется интеграл от комплексной функции? Как сводится комплексный интеграл к действительным интегралам?

3.Сформулируйте теорему Коши и обобщенную теорему Коши. Что называется интегральной формулой Коши?

4.Что называется интегралом типа Коши? Почему из существования первой производной для функции комплексной переменной следует существование производных любых порядков для этой функции?

157

Список литературы

Основная

1.Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.; Наука, 1970

2.Выгодский М.Я. Справочник по высшей математике. М.; Наука, 1976

3.Двайт Г.Б. Таблицы интегралов и другие математические формулы. М.; Наука, 1964

4.Ефимов Н.В. Краткий курс аналитической геометрии М.; 1976

5.Запорожец Г.И. Руководство к решению задач по математическому анализу. М.; 1981

6.Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов

. М.; Наука, 1986

Дополнительная

1.Берман А.Ф. и др. Краткий курс математического анализа. М.; 1973

2.Данко П.Е., Попов А.Г. и др. Высшая математика в упражнениях и задачах. М.; Высшая школа 1999

3.Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного М., Наука, 1987

158

Основные обозначения

R - множество действительных чисел

N - множество натуральных чисел

x M - x принадлежит множеству M

a;b - открытый интервал с концами a и b

a;b , a;b - полуоткрытые интервалы с концами a и b

a;b - замкнутый интервал с концами a и b

a; - бесконечный полуоткрытый интервал с левым концом a

a; - бесконечный открытый интервал с левым концом a

;b - бесконечный полуоткрытый интервал с правым концом b

;b - бесконечный открытый интервал с правым концом b i - мнимая единица

Re z - действительная часть комплексного числа z Im z - мнимая часть комплексного числа z

z - модуль комплексного числа z

z - число, комплексно сопряженное с комплексным числом z

an - числовой ряд

n 1

f n (x) - функциональный ряд

n 1
an x x0 n		- степенной ряд
n 1	f x, y dS ,		f x, y dxdy - двойной интеграл
D		D
	f x, y, z dS ,		f x, y, z dxdydz - тройной интеграл
V			V

f x, y dS ,	f x, y, z dS - криволинейные интегралы первого типа
L	L
f x, y dx g(x, y)dy , f x, y, z dx g(x, y, z)dy h(x, y, z)dz -
L	L

криволинейные интегралы второго типа

159

Предметный указатель

Аналитическая функция 153 Аргумент комплексного числа 9 Геометрическая прогрессия 68

Геометрическая форма комплексного числа 9 Двойной интеграл 105 Действительная часть комплексного числа 5 Дифференциальное уравнение 16

Дифференциальное уравнение в полных дифференциалах 24 Дифференциальное уравнение Риккати 26 Дифференциальное уравнение с разделяющимися переменными 19 Дробно-линейная функция комплексной переменной 148 Задача Коши для дифференциального уравнения 33

Задача Коши для дифференциального уравнения первого порядка 18 Задача Коши для системы дифференциальных уравнений 52 Интеграл системы дифференциальных уравнений 52 Интеграл типа Коши 160 Интегральная кривая 16 Интервал сходимости 82 Комплексная экспонента 141 Комплексно сопряженные числа 5 Комплексное число 5 Комплексный интеграл 155 Комплексный косинус 141 Комплексный логарифм 145 Комплексный синус 141 Комплексный числовой ряд 135 Корень из комплексного числа 10

Краевая задача для дифференциального уравнения второго порядка 33 Криволинейный интеграл второго типа 126 Криволинейный интеграл первого типа 123 Круг сходимости ряда 139

Линейная функция комплексной переменной 146 Линейно зависимые вектор-функции 57 Линейно зависимые функции 38 Линейно независимые вектор-функции 57 Линейно независимые функции 38

Линейное дифференциальное уравнение 36 Линейное дифференциальное уравнение первого порядка 21

Линейное неоднородное дифференциальное уравнение 45, 47 Линейное однородное дифференциальное уравнение 36 Метод вариации произвольных постоянных 45

160

Метод Даламбера 83 Метод Эйлера 26 Мнимая единица 5

Мнимая часть комплексного числа 5 Модуль комплексного числа 9 Моногенная функция 152 Необходимый признак сходимости 71

Непрерывность функции комплексной переменной 138 Общее решение дифференциального уравнения 18 Общий интеграл дифференциального уравнения 19 Однолистная функция 137

Однородная система линейных дифференциальных уравнений 59 Однородная функция 22 Однородное дифференциальное уравнение первого порядка 23 Определитель Вронского 38 Остаток ряда 69

Остаток ряда Тейлора в форме Лагранжа 92 Полярная замена переменных 111 Порядок дифференциального уравнения 16

Порядок системы дифференциальных уравнений 52 Предел комплексной последовательности 133 Предел функции комплексной переменной 137 Признак Дирихле сходимости ряда Фурье 100 Признак сравнения рядов 73 Признак сходимости Даламбера 75

Признак сходимости интегральный 75 Признак сходимости Коши 74 Признак сходимости мажорантный 140

Производная функции комплексной переменной 152 Радиус сходимости ряда 139 Расширенная комплексная плоскость 132 Ряд абсолютно сходящийся 78 Ряд гармонический 71 Ряд Маклорена 89

Ряд обобщенный гармонический 72 Ряд расходящийся 68 Ряд степенной 82

Ряд степенной комплексный 138 Ряд сходящийся 68 Ряд Тейлора 89

Ряд условно сходящийся 80 Ряд функциональный 81

Ряд функциональный комплексный 138

161

Ряд Фурье 94 Ряд числовой 67

Система дифференциальных уравнений 52 Сумма ряда 68 Теорема Абеля 82 Теорема Коши 157

Теорема Коши обобщенная 158 Теорема Лейбница 80 Теорема Пикара 30 Тройной интеграл 114 Условие Гѐльдера 99 Формула Грина 130

Формула Коши интегральная 159 Формула Маклорена 87 Формула Муавра 10 Формула Тейлора 87 Формула Эйлера 14 Формулы Коши-Римана 152

Фундаментальная система решений 39 Функция комплексной переменной 137 Характеристическое уравнение 41, 60 Цилиндрическая замена переменных 116 Частичная сумма ряда 67 Элемент ряда 67

Якобиан замены переменных 111, 116

162