заочникам / диф ур / Lectures - 3

w D1 , а

w D1

z1 t1 z2	t2 ... zn tn ... zn	tn ,	называемый
	n 1
суммой рядов.
Теорема (необходимый признак сходимости)
Если ряд zn	сходится, то lim zn 0 .
n 1	n

Определение: Ряд zn называется абсолютно сходящимся, если

n 1

сходится ряд zn .

n 1

Теорема (об абсолютной сходимости) Если ряд zn абсолютно

n 1

сходится, то он сходится.

Определение: Пусть даны два абсолютно сходящихся ряда

Тогда произведением этих рядов называется ряд cn , где

n 0

Замечание: a0 a1 a2 a3 ... b0 b1 b2 b3 ...

an	и bn .
n 0	n 0

n

cn ak bn k . k 0

a0b0 a0b1 a1b0 a0b2 a1b1 a2b0 a0b3 a1b2 a2b1 a3b0 ...

	Функции комплексной переменной
Пусть даны	две расширенные	комплексные плоскости z x iy и
w u iv ,	и пусть D - множество точек на плоскости z x iy			и D1 -
множество точек на плоскости w u iv .
Определение: если задан закон		f	, по которому каждому числу	z D
сопоставляется число w D1 ,		то	говорят, что w f (z) есть функция
комплексной переменной. При этом			z D называется прообразом точки

называется образом точки z D .

Замечание 1: понятия области определения и области значений функции полностью переносятся из курса математического анализа.

133

Замечание 2: к сожалению, невозможно нарисовать график функции комплексной переменной, т.к. пришлось бы изображать на плоскости 4 оси координат: x, y, u, v .

Определение: взаимно-однозначная функция комплексной переменной называется однолистной функцией.

Поскольку w u iv f (z) и z x iy , то u u x, y и v v x, y , и, следовательно, w u x, y iv x, y

Определение: Говорят, что функция f (z) : C C имеет предел,

равный

A при

z a (и пишут

lim f (z) A ), если для любого (как угодно

z a

малого)

действительного

числа 0

найдется действительное

число

0 такое, что если

z a

, то и

f (z) A

.

Определение: Говорят, что функция f (z) : C C имеет предел,

равный

бесконечности при z a (и пишут lim f (z) ), если для любого (как
				z a
угодно большого) действительного числа					E 0 найдется действительное
число 0 такое, что если		z a		,	то и		f (z)		E .

Определение: Говорят, что функция

f (z) : C C имеет предел,

равный

A при

z (и пишут

lim f (z) A ), если для любого (как угодно

z

малого)

действительного

числа 0 найдется действительное

число

0 такое, что если

z

, то и

f (z) A

.

Теорема (предел и арифметические операции)

Если lim f (z) A и lim g(z) B , то
z a	z a
1)	lim f (z) g(z) A B
	z a
2)	lim f (z) g(z) A B
	z a
3)	lim f (z) g(z) A B
	z a
4)	lim	f (z)		A	, если B 0
	z a	g(z)		B

134

			_____
	5) lim f z
					A
		z a
Без доказательства.
Определение:	Если		функции f (z) определена в точке z0								и для нее
выполняется равенство			lim f (z) f (z0 ) , то функция							f (z)	называется
			z z0
непрерывной в точке z0 .
Рассмотрим	последовательность						функций		f1 z ,	f2 z ,..., fn z ... и
составим из них ряд		f1 z		f 2 z			...	f n z ... f n z .
									n 1
Определение:	Ряд	f1 z		f 2 z ...				f n z ... f n z			называется
									n 1
функциональным рядом.

Если в функциональный ряд вместо переменной z подставить какое-либо комплексное число, получится сходящийся или расходящийся числовой

ряд. Пусть D - множество всех значений переменной z , при которых ряд

	z сходится. Тогда можно говорить, что на множестве комплексных
f n
n 1
чисел	D	определена функция одной комплексной переменной
		z , значениями которой являются суммы соответствующих
F (z) f n

n 1

числовых рядов.

Определение: Множество чисел D , при которых сходится ряд f n z ,

		n 1
называется областью сходимости этого ряда.
Определение: Если	f n z an z z0 n , где z0 , an - комплексные числа,
то ряд an z z0	n a0 a1 z z0 a2 z z0 2	... называется

n 0

степенным рядом.

135

Теорема	Абеля (о	круге	сходимости)						Степенной	ряд
an z z0 n сходится в		открытом		круге		z z0			R , (где	R -
n 0
некоторое	действительное	число)	и	расходится вне					замкнутого	круга

z z0 R .

Без доказательства.

Замечание: число R называется радиусом сходимости ряда.

Теорема (о радиусе сходимости ряда) Если существует предел

	l lim n		a	n		,
	n						1
	то радиус сходимости ряда вычисляется по формуле R							.
							l

Теорема (мажорантный признак сходимости Вейерштрасса)

	z z0	n начиная с
Если для любого z каждый элемент ряда an
n 0

некоторого номера по модулю не больше соответствующего слагаемого bn

сходящегося действительного числового ряда

bn с положительными

n 0

слагаемыми ,

то

ряд an z z0 n

абсолютно

сходится

при

любом

n 0

значении z.

z

n

Пример: Найти радиус сходимости ряда

.

n 0

n!

z n

z

n

z

Решение:

. Поскольку

-

действительное число

и ряд

n!

n

!

n

сходится

при

любом

действительном

значении

,

то по

n!

n 0

z

n

мажорантному

признаку

сходимости

ряд

сходится

при

любом

и радиус сходимости равен .

n 0 n!

значении z

136

Контрольные вопросы:

1.Что называется расширенной комплексной плоскостью? Что называется окрестностью точки на расширенной комплексной плоскости?

2.Что называется пределом последовательности комплексных чисел? Как свести вычисление комплексного предела к вычислению пределов действительных последовательностей? Что называется рядом комплексных чисел, каковы его свойства?

3.Что называется функцией комплексной переменной? Что называется пределом функции комплексной переменной, каковы его свойства?

4.Что называется комплексным степенным рядом? Что является областью сходимости такого ряда? Что такое мажорантный признак сходимости?

Лекция 16(50) Элементарные функции комплексной переменной и их свойства

Экспоненциальная и тригонометрические функции

z

n

Как было показано в предыдущей лекции, степенной ряд

сходится

n 0

n!

n

на всей комплексной плоскости. Полагаем e z

z

, т.е. определяем

n 0 n!

экспоненциальную

функцию

как

сумму

степенного

ряда.

Если x -

n

действительное число, то получим

e x

x

, что совпадает с рядом

n 0 n!

Маклорена действительной экспоненциальной функции.

z

n

t

n

Рассмотрим произведение рядов e z

и

et

:

n 0 n!

n 0

n!

zn

tn

z2

t2

z3

z2

t2

t3

1

z t

zt

t z

...

2!

3!

2!

2! 3!

n 0

n! n 0

n!

2!

1 z t

z 2

2zt t 2

z 3 3z 2t 3zt 2

t 3

...

2!

3!

1

z t

z t 2

z t 3

... ez t

1!

3!

2!

Таким образом, для любых комплексных чисел справедлива формула

ez t e z et
Полагая в этой формуле t w, получим ez e w	ez w .

137

Аналогично, опираясь на ряды Маклорена действительных функций, определим комплексные синус и косинус:

		1 n 1 z 2n 1		1 n z	2n
	sin z		, cos z		.
		2n 1 !		2n !
	n 0		n 0

Можно показать , что эти ряды абсолютно сходятся на всей комплексной плоскости. Кроме того, из определения комплексных синуса и косинуса следует, что

sin(z) sin z , cos(z) cos z

iz

iz

iz

iz

iz

n

2

3

4

5

Рассмотрим eiz

1 iz

5! ...

n!

2!

3!

4!

n 0

1 iz

z 2

i

z 3

z 4

i

z 5

...

2!

3!

4!

5!

z 2

z 4

z 3

z 5

1

...

i z

...

cos z i sin z

2!

4!

3!

5!

Таким образом, доказана формула

eiz

cos z i sin z ,

откуда при z x R следует формула Эйлера, приведенная в первой

лекции.

ei z 2 cos z 2 i sin z 2 cos z i sin z ,

Поскольку eiz 2 i

то экспоненциальная функция является периодической с наименьшим

периодом 2i .

Рассматривая совместно с рядом

iz

iz

iz

iz

iz

n

2

3

4

5

eiz

n!

1 iz

... ряд

2!

3!

4!

5!

n 0

iz

iz

iz

iz

iz

e iz

n

2

3

4

5

1 iz

...,

n!

2!

3!

4!

5!

n 0

складывая и вычитая эти два ряда, получим формулы

eiz

e

iz

eiz

e iz

cos z

;sin z

.

2

2i

138

Рассмотрим выражение: eiz e iz eit e it eiz e iz eit e it :

eiz e iz eit e it eiz e iz eit e it ei z t ei t z

ei z t e i z t ei z t ei t z ei z t e i z t 2 ei z t ei z t ,

значит,

cos z t cos z cos t sin z sin t

Аналогично можно доказать, что

cos z t cos z cos t sin z sin t sin z t sin z cos t cos z sin t , sin z t sin z cos t cos z sin t .

Отсюда, полагая z t , получим формулы синуса и косинуса двойного угла:

sin 2z 2sin z cos z , cos 2z cos 2 z sin 2 z ,

а полагая t z в формуле cos z t cos z cos t sin z sin t , получим cos 2 z sin 2 z 1.

Легко проверяется, что функция w e z не обращается в 0 ни при каких значениях переменной z :

e z e x iy e x eiy ex cos y i sin y .

Поскольку e x 0 , а синус и косинус ни при каком действительном значении угла не обращаются в 0 одновременно, то и e z 0 .

Кроме того, синус обращается в 0 только при z k, k Z , а косинус –

при z k, k Z . 2

Поскольку cos z 2 14 e 2 y e2 y 12 cos 2x , то комплексный косинус

является неограниченной функцией. Аналогично можно доказать неограниченность комплексного синуса.

Комплексные тангенс и котангенс определяются привычными формулами

	tgz	sin z	, ctgz	cos z	.
		cos z		sin z
Поскольку функция	w e z	периодична с периодом 2i , то изучение ее
поведения можно	ограничить областью			0 y 2 на комплексной

139

плоскости.	Введем в	плоскости		UOV полярные координаты,							тогда
w e z e x cos y i sin y ei .
Рассмотрим прямую y y0 .
В точках	этой прямой	w e x cos y				0	i sin y		0	ei 0 , то есть угол
постоянен, а модуль может быть любым.								Это значит, что прямые			y y0
переходят в лучи, выходящие из начала координат.
Рассмотрим вертикальный отрезок			x x0					при y 0;2 . В точках этого
отрезка w e x0 cos y i sin y				0	ei ,			значит модуль постоянен, а угол

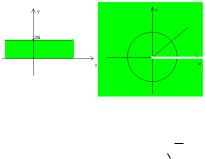
может быть любым и, следовательно, эти отрезки переходят в окружности с центром в начале координат. Вся полоса 0 y 2 перейдет при

отображении w e z в комплексную плоскость с удаленным лучом 0 .

Рис. 28 Область однолистности экспоненты

Функции w z n и w nz .

Из

формулы

Муавра

z n

n cos n i sin n следует, что

отображение,

осуществляемое

функцией w z n сводится к повороту

каждого вектора на угол

n 1 против часовой стрелки и растяжению

(при

z

1) или сжатию (при

z

1 ) в

z

n 1 раз.

Функция		w z n , очевидно,				не	является
	cos i sin ,								2
z			z	2	cos
1
									n
z n z n		n cos n i sin n .
1	2

однолистной. т.к. если

		2
	i sin		, то
		n

140

Любые

две

не совпадающие

точки

z1 1 cos 1 i sin 1 ,

z

cos

i sin

лежащие

внутри

угла 0

2

при

2

2

2

2

n

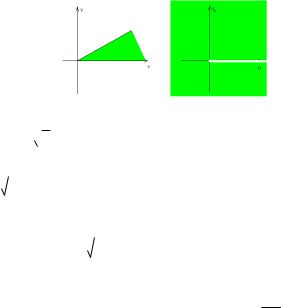
отображении w z n перейдут в разные образы.

При этом

угол

0

2

отобразится в

комплексную плоскость с

n

удаленным лучом 0 .

Рис. 29 Область однолистности степенной функции

Функция w nz , очевидно, является n -значной. Это следует уже из рассмотренной ранее формулы

wk

2 k

i sin

2 k

k 0,1,2,..., n 1.

n cos

n

,

n

Главным значением корня степени n будем считать

w0

i sin

n cos

n

n

эта функция осуществляет взаимно однозначное отображение комплексной плоскости с удаленным лучом 0 на угол 0 2n .

Логарифмическая и обратные тригонометрические функции

Определение: Логарифмическая функция – это функция обратная к экспоненциальной (показательной), т.е. число w называется логарифмом числа z , если ew z :

w ln z .

Замечание: из определения логарифма следует его основное свойство:

ln z

z

2

ln z

ln z

2

. Действительно, если

z ew1

и z

2

ew2

, то

1

1

1

z z

2

ew1 ew2

ew1 w2

1

141

0 y 2 .

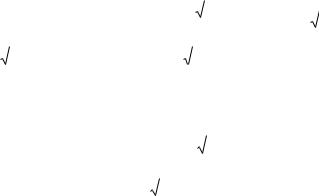
Пусть z cos i sin ei , тогда

ln z ln ei ln ln ei ln i

Поскольку	cos 2k cos	и sin 2k sin при	любом
целом значении k , то любое, не		равное 0, комплексное число имеет
бесконечное	множество различных	логарифмов. Если 0;2	, то

функцию ln z ln i будем называть главным значением логарифма. Эта функция осуществляет взаимно однозначное отображение комплексной плоскости с удаленным лучом 0 на полосу

Пример: найти ln i
		i sin				i		i
Решение: i 1 cos				, значит, ln i 0
	2		2			2		2

Рассмотрим

функцию,

обратную к

синусу

(арксинус). Выразим из

равенства

z sin w

eiw e iw

переменную

w :

eiw e iw 2iz ,

2i

e2iw 2izeiw 1 0 .

2iz

4z 2 4

eiw

iz

1 z 2 ,

2

iw ln iz

,

w i ln iz

.

1 z 2

1 z 2

Таким

образом,

комплексный арксинус выражается через комплексный логарифм. При этом можно выбирать любое из двух значений квадратного корня и любое из значений логарифма.

Аналогично формуле arcsin z i ln iz										можно вывести
									1 z 2
формулы для арккосинуса и арктангенса.
arcsin z i ln z
					z 2		1
arctgz	i	ln	1	iz		.
2		1		iz

Линейная функция

Определение: функция w az b , где a, b - комплексные числа, называется линейной.

142