заочникам / диф ур / Lectures - 3

b;b . Для этой функции можно составить ряд Фурье, но уже нельзя гарантировать, что он будет содержать только синусы или только косинусы.

Контрольные вопросы:

1.Что называется рядом Фурье заданной функции? В чем преимущества и недостатки ряда Фурье о сравнению с рядом Тейлора? Как находятся коэффициенты ряда Фурье?

2.При каких условиях существует ряд Фурье для заданной функции на симметричном промежутке? Сформулируйте признак Дирихле и покажите, что ряд Фурье кусочномонотонной и кусочно-непрерывной функции во всех точках непрерывности сходится к этой функции.

3.Покажите, что на промежутке 0;l функцию, удовлетворяющую условию

Гѐльдера, можно представить рядом Фурье, не содержащим синусов или не содержащим косинусов.

4.Покажите, что функцию, удовлетворяющую условию Гѐльдера можно представить рядом Фурье на любом конечном промежутке.

Задачи для самостоятельного решения:

1. Доказать, что любую функцию, заданную на симметричном промежутке, можно представить в виде суммы четной и нечетной функций.

2. .Доказать,

что

если

функция

y x

нечетная, то

ее

ряд Фурье на

промежутке

;

x

имеет

вид

bn sin nx ,

а

если

четная,

то

n 1

x

a0

an cos nx

.

2

n 1

3. Доказать, что если функция имеет на промежутке a;b непрерывную производную, то она

удовлетворяет условию Гѐльдера.

Лекция 12(46) Двойной интеграл

Задачи, приводящие к понятию двойного интеграла

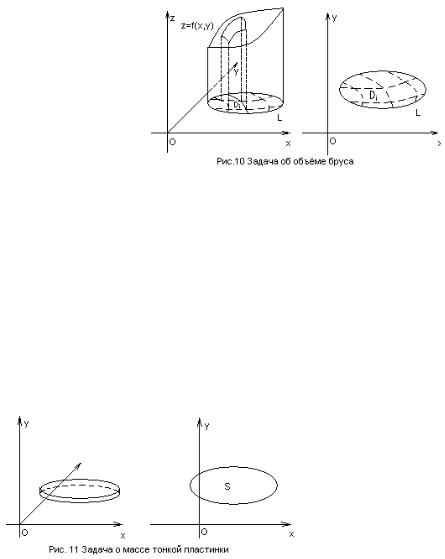
1) Задача об объеме цилиндрического бруса

Рассмотрим

тело,

ограниченное

произвольной

поверхностью

z f x, y 0 ,

координатной

плоскостью

XOY и

цилиндрической

поверхностью с образующей, параллельной оси

OZ .

Требуется найти

объем данного тела.

Пусть указанная

цилиндрическая

поверхность

пересекает

плоскость

XOY по

замкнутой

линии

L ,

ограничивающей

плоскую область

D .

Поделим эту область сетью линий на более мелкие области D1 , D2 ,..., Dn и

103

рассмотрим ряд цилиндрических «столбиков», у которых нижними основаниями являются области D1 , D2 ,..., Dn .

В каждой области Di

выберем		по
произвольной		точке
i xi , yi	.	Если

приближенно рассматривать каждый «столбик» как обобщенный цилиндр высоты

zi f xi , yi , то его

объем	Vi	будет
приближенно равен Vi f xi , yi			Si , где Si		-	площадь области	Di .
Объем	всего	цилиндрического	бруса	равен	сумме объемов		всех
«столбиков»:
		n	n
		V Vi f xi , yi Si
		i 1	i 1
Устремим n таким образом, чтобы				max Si		0 (геометрически

это означает, что область D делится на все большее количество все более мелких областей), тогда

n

V lim f xi , yi Si

n i 1Si 0

2) Задача о массе тонкой пластинки

Дана тонкая пластинка высоты h и переменной плотности, которую в связи с небольшой высотой пластинки можно считать не меняющейся по высоте. Требуется

найти массу пластинки.

Поместим пластинку в прямоугольную систему координат так, чтобы параллельные плоскости пластинки были параллельны координатной

104

плоскости XOY , тогда плотность будет функцией координат x, y :x, y . Обозначим через S проекцию пластинки на плоскость XOY , площадь этой проекции обозначим S . Если бы плотность была

постоянной, то масса пластинки была бы равна произведению плотности на объем m V h S .

Поделим область S сетью линий на более мелкие области S1 , S2 ,..., Sn ,

площади которых обозначим S1 , S2 ,..., Sn , В каждой из этих областей
выберем по точке i xi , yi	и будем приближенно считать, что в области
Si плотность постоянна	и равна xi , yi . Тогда масса пластинки

приближенно равна

n		n
m h xi , yi Si		h xi , yi		Si
i 1		i 1
Значит, устремляя n так, чтобы max Si			0 , получим
	n
m h lim	xi , yi Si
n	i 1
Si 0

Заметим, что при рассмотрении обеих задач были получены сходные выражения.

Определение: Пусть в области				D на плоскости	XOY задана функция
z f x, y . Поделим область				D произвольными линиями на меньшие
области D1 , D2 ,..., Dn		с площадями S1 , S2 ,..., Sn и в каждой из этих
областей выберем по точке i xi , yi . Если существует предел
			n
		lim	f xi , yi Si ,
		n	i 1
		Si 0			f x, y по области D
то он называется двойным интегралом от функции
и обозначается
		f x, y dS или f x, y dxdy .
		D		D
Замечание: если функция z f				x, y непрерывна в области D , то предел
	n
lim	f xi , yi Si	существует. Это условие является достаточным для
n	i 1
Si 0

существования двойного интеграла, но не является необходимым. Можно

105

привести примеры разрывных функций, для которых существует двойной интеграл.

Сведение двойного интеграла к повторному

Теорема (свойства двойного интеграла)
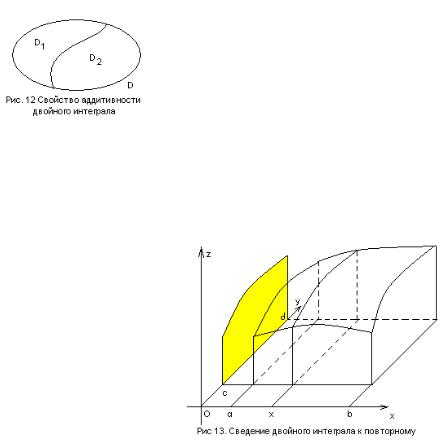
1)	Пусть дана	область	D	такая,	что
D D1 D2 и		при	этом	площадь
пересечения областей D1 и D2 равна 0,
тогда
f x, y dS f x, y dS f x, y dS
D	D1		D2
2) Для любого числа :
f x, y dS f x, y dx
D	D
3) f x, y g x, y dS f x, y dx g x, y dy ,				если	оба
D	D	D

интеграла в правой части равенства существуют.

Без доказательства.

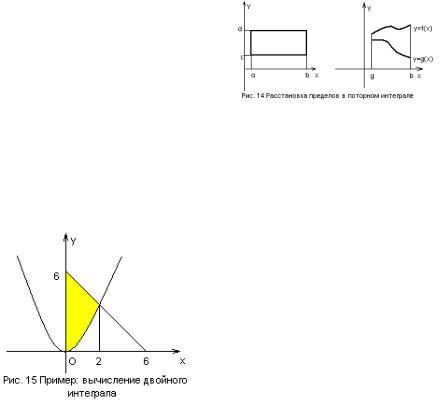
Рассмотрим положительную функцию z f x, y 0 и

цилиндрический брус, ограниченный графиком этой функции, координатной плоскостью XOY и плоскостями

x a, x b, y c, y d .

Площадь сечения цилиндрического бруса плоскостью, параллельной координатной плоскости

ZOY и пересекающей ось

OX в точке x , обозначим S x . Тогда объем цилиндрического бруса будет

b

равен S x dx . Спроектировав это сечение на плоскость ZOY , получим

a

d

криволинейную трапецию, площадь которой равна f x, y dy .

с

106

Значит,		b d
	f x, y dS f x, y dy		dx .
D		a c
Можно	было,	рассматривая	сечения	бруса	плоскостями,
перпендикулярными оси OY , получить
		d b
	f x, y dS f x, y dx dy
	D	c a

Если в плоскости XOY задан не прямоугольник, а фигура, ограниченная прямыми x a, x b и графиками

функций y f x , y g x , то

	b f x
	f x, y dS	f x, y dy dx ,
D	a g x
т.е.	внутренний	интеграл	по

переменной y имеет пределы, зависящие от переменной x .

Пример 1: Вычислить интеграл x y dS по области D , ограниченной

D

линиями x 0, y x2 , y 6 x при условии x 0 .
Решение:
Найдем	абсциссу точки	пересечения
линий	y x2 , y 6 x :	x2 6 x ;

x2 x 6 0 ; x1 3, x2 2 .

Врассматриваемой области переменная

xизменяется в пределах 0;2 . При

x0;2 переменная y будет

изменяться от точки на линии				y x 2
до точки на линии y 6 x , значит,
	2	6 x
x y dS			x y dy dx .
D	0		x2
				107

6 x

Вычисляем сначала внутренний интеграл

x y dy :

x2

6 x

y 2

6 x

6 x 2

x y

dy

xy

x 6

x

2

2

x2

x2

x

2

2

x x2

6x x2

1

x2

12x 36 x3

2

2

x4 x3 3 x2 12x 18 2 2

x4

2

Теперь подставим полученную функцию под знак внешнего интеграла:

2	x4			3
		2	x3	2	x2 12x 18 dx
0

	2	x4			3
и вычислим его:			2	x3	2	x2 12x 18 dx
	0

x5			x4		x3				2
						6x2	18x		8,8
	10		4		2
									0
Пример 2: Вычислить интеграл									xydS по области D , ограниченной

D

линиями y 0, y x, y 2 x .

Решение (первый способ):

Линии y x, y 2 x , как нетрудно проверить, пересекаются в точке x 1. В полученной области переменная x изменяется в пределах0;2 , но, в зависимости от того, какому

из интервалов 0;1 или 1;2 принадлежит x , переменная y будет изменяться от линии y 0 и до линии

y x или y 2 x . Поэтому:

108

																									1																			2 2 x
																																x
											xydS
																														xydy dx																			xydy dx .
											D													0						0														1					0
																						x								2
															x																															1
	x							xy 2																					x											x2												x
xydy
								2																2											0						2		;							xydy								dx
0												0																																	0					0
																								x 2 x 2
2 x									xy 2					2 x																														x3 4x												2 4x
xydy																																						0																								;
								2																				2																						2
0														0
2				2 x													2			x3				4x2 4x																			1 x4														4x3
						xydy dx																						2										dx					2					4								3				2x
1 0																	1
			1				32														1			1						4											1				4					11								5
					4								8																						2																											.
			2					3													2			4						3											2				3 12													24
2 2 x																	1							5						9
				xydy dx													6							24						24
0				0

1x 2

0 2

2

1

dx 16 ;

Второй способ: начнем расстановку пределов интегрирования не с

переменной x , а с переменной																									y . В рассматриваемой области переменная
y			изменяется в пределах 0;1 .																							При этом переменная x изменяется от
точки на линии y																		x y 2								до точки на линии y 2 x x 2 y .
																x
															1		2 y
Поэтому xydS																		xydx dy .
							D								0 y2
2 y										2		2 y				2 y				2							y		2	2			3	4 y	2	4 y y	5
xydx								x			y											y								y		y
										2									2										2							2
y2												y2
1			2 y												1
			xydx dy											1	y 3 4 y 2										4 y y 5 dy
			y		2							2			0
0
	1				y 4				4 y 3										y 6					1			9
															2 y 2
	2				4						3								6					0			24

109

D , тогда

Замена переменных в двойном интеграле

Определение: Пусть переменные x, y являются функциями независимых переменных u, v : x x u, v , y y u, v . Тогда определитель

	x	x
J u, v	u	v
	y	y
	u	v

называется якобианом замены переменных.

Пример (полярная замена переменных)

Пусть x cos, y sin , тогда

x

cos,

x

sin ,

y

sin,

y

cos ,

x

x

cos

sin

J ,

cos

2

sin

2

y

y

sin

cos

.

Замечание: полярная замена координат обычно используется в случае, когда область интегрирования ограничена прямыми и окружностями.

Теорема (о замене переменных)

Пусть x x u, v , y y u, v - непрерывные функции, осуществляющие взаимно однозначное отображение области D' на область

f x, y dS f x u, v , y u, v J u, v dS

	D	D'
	Без доказательства.
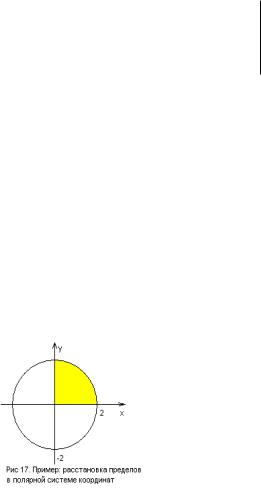
Пример: Вычислить интеграл x2 y 2		2 dS , если область D задана
	D
условиями x2 y 2 4 ,	x 0, y 0 .

Решение:

110

Интегрирование происходит по четверти круга x2 y 2 4 , расположенной в первом координатном углу. В этой области переменная

изменяется в пределах			, и, независимо от нее, переменная
	0;
		2
изменяется в пределах 0;2 . Якобиан полярной замены равен				, поэтому

x 2

D

		2	2	2									2
y							cos				sin
	2					2		2		2		2
			0	0

2	2		5		2	32			16
								d
				d d			3		3
0		0			0

Контрольные вопросы:

1.Что называется двойным интегралом? При каких условиях существует двойной интеграл?

2.Сформулируйте свойства двойного интеграла.

3.Сформулируйте алгоритм сведения двойного интеграла к повторному.

4.Как производится замена переменных в двойном интеграле? Что называется якобианом замены переменных? Что называется полярной заменой переменных?

Задачи для самостоятельного решения:

1.доказать теорему о свойствах двойного интеграла.

2.Доказать, что площадь фигуры D на плоскости вычисляется по формуле S dxdy .

D

Лекция 13(47) Тройной интеграл. Приложения двойных и тройных интегралов к задачам геометрии и механики

Тройной интеграл

Пусть дано некоторое тело V переменной плотности в пространственной системе координат и в каждой его точке M x, y, z известна плотностьx, y, z . Требуется определить массу тела.

Поделим тело V сетью поверхностей на более мелкие		тела V1 ,V2 ,...,Vn и в
каждом теле Vi выберем по точке M i xi , yi , zi .		Будем приближенно
считать,	что в каждом теле Vi плотность постоянна и равна плотности
xi , yi	, zi в выбранной точке. Тогда масса тела Vi приближенно равна

111

mi xi , yi , zi Vi , где	Vi - объем тела Vi . Масса всего тела будет
	приближенно равна
	n	n
	m mi	xi , yi , zi		Vi
	i 1	i 1
	Устремим	n	так,	чтобы
	max Vi 0 , тогда
		n
	m lim	xi , yi , zi Vi
	n	i 1
	Si 0
	Определение:		Пусть	в
	пространственной области V задана
	функция	трех	переменных
	f xi , yi , zi	. Поделим область V

произвольными поверхностями на области V1 ,V2 ,...,Vn и в каждой из этих областей выберем по точке M i xi , yi , zi . Если существует предел

				n
			lim	f xi , yi , zi Vi		,
			n
			Si 0 i 1
где Vi	- объем тела Vi , то этот предел называется тройным интегралом
от функции		f x, y, z по области V и обозначается
			f x, y, z dV		или f x, y, z dxdydz .
			V		V
Замечание:		если функция		z	f x, y, z непрерывна		в области V , то
			n	Vi существует.
предел	lim		f xi , yi , zi			Это	условие является
	n		i 1
	Si	0

достаточным для существования тройного интеграла, но не является необходимым. Можно привести примеры разрывных функций, для которых существует тройной интеграл.

Теорема (свойства тройного интеграла)

1) Пусть дана область V такая, что V V1 V2 и при этом объем пересечения областей V1 и V2 равен 0,

112